CAPÍTULO 2 RETIFICADORES A DIODO RETIFICADOR MONOFÁSICO DE MEIA ONDA A DIODO. a) Carga Resistiva Pura
|
|
|
- Bernardo Aquino Morais
- 8 Há anos
- Visualizações:
Transcrição
1 CAPÍTULO ETFCADOES A DODO.1 ETFCADO MONOFÁSCO DE MEA ONDA A DODO a) Carga esistiva Pura A estrutura d retificadr mnfásic de meia nda alimentand uma carga resistiva está representada na figura.1. v D D v(t) v L Fig..1 etificadr mnfásic de meia nda cm carga resistiva. O did blqueia semicicl negativ da tensã alternada de alimentaçã v(t). Desse md, smente s semicicls psitivs sã aplicads à resistência de carga. As frmas de nda relativas à estrutura em questã estã representadas na figura..
2 Cap. etificadres a Did 9 v t v L t t v D t Fig.. Frmas de nda relativas à figura.1. A tensã de alimentaçã é representada pela expressã (.1). v( t) sen ( t) (.1) A tensã média na carga é calculada pela expressã (.). Assim, 1 sen ( t) d( t) (.) cs( t) u, 45 (.) A crrente média na carga é btida pela expressã (.4). 1 sen ( t ) d ( t ) (.4) Assim: 1 1 sen ( t) d( t) (.5) (.6)
3 Cap. etificadres a Did Ou ainda:, 45 (.7) A crrente de pic n did, igual à crrente de pic na carga, é dada pela expressã (.8). Dp (.8) A tensã de pic inversa n did é dada pela expressã (.9). Dp (.9) btida a seguir. Para dimensinament crret d did, é imprtante cnhecer a sua crrente eficaz, Lef 1 sen ( t) d( t) (.1) Lef sen t d t ( ) ( ) (.11) t sen ( t) Tmandse: sen ( t) d( t) 4 (.1) Obtémse: Lef, 77 (.1) b) Carga L A estrutura d retificadr mnfásic de meia nda alimentand uma carga L está representada na figura.. v(t) v D D L v Fig.. etificadr mnfásic de meia nda alimentand carga L. As frmas de nda relativas à carga L estã representadas na figura.4. l v v L
4 Cap. etificadres a Did 1 Devid a presença da indutância, did nã se blqueia quand t =. O blquei crre n ângul, que é superir a. Enquant a crrente de carga nã se anula, did se mantém em cnduçã e a tensã de carga, para ânguls superires a, trnase instantaneamente negativa. A crrente de carga é btida pela sluçã da equaçã diferencial (.14) sen ( t) = L d i ( t) L ( t) (.14) dt v t v L t v D t Fig..4 Frmas de nda relativas à figura.. A sluçã da equaçã diferencial (.14) é representada pela expressã (.15). i L t ( t) sen( t ) e 1( ) (.15) X X Onde: arc tg X = L L
5 Cap. etificadres a Did A crrente da carga é cmpsta de duas cmpnentes distintas, representadas pelas expressões (.16) e (.17). i 1 ( t) sen ( t ) (.16) X i( t) 1( ) e t / (.17) As duas cmpnentes estã representadas graficamente na figura.5. Para t =, temse (t) =. Assim: 1 X sen( ) (.18) t/ Prtant, il( t) sen( t ) sen( ) e X (.19) () 1 i i 1 t () 1 Fig..5 Crrente de carga relativa à figura.. A cmpnente i (t) representa a parcela transitória da crrente; a cmpnente i 1 (t) representa a respsta em regime permanente da carga L submetida à tensã alternada da rede. Para que se pssa estabelecer valr médi da tensã na carga, é necessári que se cnheça ângul. De acrd cm a figura.4, i(t) = quand t =. Levandse estes valres na expressã.19 btémse a expressã (.). / sen ( ) sen ( ) e (.) L Cm tg, pdese escrever: / tg sen ( ) sen ( ) e (.1)
6 Cap. etificadres a Did Esta funçã implícita, a ser reslvida numericamente, dá cm resultad a curva mstrada na figura Fig..6 Ângul de cnduçã em funçã d ângul, para a figura.. Uma vez cnhecid ângul de cnduçã, pdese determinar valr médi da tensã de carga. O prcediment está descrit a seguir. 1 sen ( t) d( t) (.) cs( t) Assim, ( 1 cs ) (.) Ou:, 5 ( 1 cs ) (.4) De acrd cm a expressã (.4), a presença da indutância causa uma reduçã na tensã média na carga. A seguir é descrit prcediment destinad a estabelecer valr médi da tensã n indutr. Na figura.7 estã representadas a tensã de carga, a crrente de carga, a tensã n resistr v (t) e a tensã n indutr v l (t).
7 Cap. etificadres a Did 4 v v l m S l v m S i t Fig..7 Frmas de nda para circuit da figura.. De acrd cm a expressã (.14), quand i(t) alcança seu valr máxim, temse d i( t). Pr ist, nesse instante, quand t = m, temse v l (t) = e v (t) = v(t). A tensã dt média n indutr é calculada d seguinte md: lmed 1 T t m t vl( t) dt vl( t) dt t m (.5) Assim: l ( t ) dt Ldi (.6) lmed 1 m Lm Lm T Ldi Ldi 1 T (.7) m Assim: lmed (.8) Cncluise prtant que valr médi da tensã na indutância é nul. Este fat indica também que S 1 = S. Mas S 1 u S representam flux prduzid n indutr. Desse md, valr médi nul da tensã indica que indutr é desmagnetizad a cada cicl de funcinament da estrutura. A seguir, é descrit prcediment que estabelece valr da tensã média na resistência de carga. Prtant, Cm lmed lmed med (.9) btémse: (.) med, 5 ( 1 cs ) (.1) med Pr ist a crrente média na carga e n did é btida pela expressã (.).
8 Cap. etificadres a Did 5, 5 ( 1 cs ) (.) A crrente média na carga pde também ser btida d seguinte md: 1 t/ sen ( t ) sen ( ) e d( t) Z De md análg, pdese estabelecer valr eficaz da crrente de carga: (.) Lef 1 t / Z sen ( t ) sen ( ) e d( t) (.4) Z Seja: md (.5) E, ef Z Lef (.6) Send: Z X (.7) 1 t/ Assim: md ( t ( sen ) sen ) e d( t) 1 ef sen sen e t / ( t ) ( ) d ( t) (.8) Desse md, md e ef pdem ser btids numericamente em funçã de. Tais funções estã representadas na figura.8. 1,4 1, 1,,8,6,4 ef md, Fig..8 alres médi e eficaz da crrente de carga para a figura..
9 Cap. etificadres a Did 6 c) Carga L cm Did de "dalivre" Para evitar que a tensã de carga trnese instantaneamente negativa devid à presença da indutância, empregase did de "rdalivre". A estrutura adquire assim a frma apresentada na figura.9. D 1 v(t) D L L Fig..9 etificadr de Meia Onda cm Did de "dalivre". O circuit apresentad na figura.9 apresenta duas etapas de funcinament, representadas nas figuras.1.a e.1.b. D 1 D L L vl v vl v (a) v D 1 D L L v L (b) Fig..1 Etapas de funcinament d retificadr cm did de "rdalivre". A primeira etapa crre durante semicicl psitiv da tensã v(t) de alimentaçã. O did D 1 cnduz a crrente de carga e did D L, plarizad reversamente, encntrase blquead. A segunda etapa crre durante semicicl negativ da tensã v(t). O did D 1, plarizad reversamente, se blqueia. A crrente de carga, pr açã da indutância, circula n did de "rdalivre" D L. As frmas de nda relativas a retificadr de meia nda cm did de "rdalivre" estã representadas na figura.11.
10 Cap. etificadres a Did 7 v t v L t t Fig..11 Frmas de nda para a estrutura da figura.9. Se a crrente de carga se anula em cada cicl de funcinament da estrutura, a cnduçã é dita descntínua; cas cntrári ela é dita cntínua. O fat da cnduçã trnarse cntínua u nã, é cnseqüência da cnstante de temp da carga. Para cnstantes de temp elevadas a cnduçã pde ser cntínua. A cnduçã cntínua pde apresentar interesse prátic, pis implica numa reduçã das harmônicas da crrente de carga. Para se fazer a análise matemática da crrente de carga, supõese a estrutura funcinand em regime permanente e cnduçã cntínua. Tal situaçã está representada na figura.1. Uma maneira simples de se bter a crrente de carga cnsiste n empreg da Série de Furier. Decmpndse v L (t) btémse: t t t vl t sen t cs( ) cs( 4 ) cs( 6 ) ( ) ( ) (.9)
11 Cap. etificadres a Did 8 v L t t Fig..1 Tensã e crrente de carga para cnduçã cntínua. Assim, a tensã e a crrente média de carga serã:, 45 (.4), 45 (.41) A expressã da crrente de carga será: i( t) i1( t) i( t) i4( t) i6( t) in( t) (.4) Onde: i1( t) Z sen ( t 1) 1 (.4) i( t) cs( t ) 1Z (.44) i4( t) cs( 4t 4 ) 5Z4 (.45) i6( t) cs( 6t 6) 5 7Z6 (.46) in( t) ( n 1) ( n 1) Zn cs( nt n ) (.47) Onde: n 1
12 Cap. etificadres a Did 9 Z n L (.48) n n tg 1 n L (.49) O valr eficaz da crrente de carga é dad pela expressã (.5). Lef L1 L L4 L6 Ln (.5) Onde: L1 (.51) Z1 L L4 Z 15 Z Ln ( n 1)( n 1) Zn 4 (.5) (.5), n 1 (.54) Os valres médis das crrentes ns dids pdem ser cnsiderads iguais à metade d valr calculad para a carga, quand a cnstante de temp fr elevada. d) Us d Transfrmadr Em muitas aplicações, retificadr é alimentad a partir de um transfrmadr, que apresenta as seguintes prpriedades: permite a adaptaçã da tensã da fnte à tensã da carga; permite islament galvânic entre a rede e a carga. A estrutura d retificadr mnfásic de meia nda cm did de rdalivre alimentad pr transfrmadr está representada na figura.1. v(t) i1 N1 N D1 i v i D L D L L Fig..1 etificadr mnfásic de meia nda alimentad pr transfrmadr. Para simplificar a análise d funcinament da estrutura, a crrente de carga i(t) será cnsiderada isenta de harmônicas, hipótese que só é rigrsamente verdadeira quand a
13 Cap. etificadres a Did 4 indutância de carga fr infinita. O transfrmadr será cnsiderad de ganh unitári, sem perda de generalidade. As crrentes envlvidas estã representadas na figura.14. A crrente magnetizante d transfrmadr será cnsiderada nula. i t t i DL t CC t i CA t i1 t Fig..14 Frmas da nda para a estrutura da figura.1. Seja Assim: Decmpndse a crrente secundária i (t) em Série de Furier btémse: i i ( t) cs( t) cs( t ) cs( 5t ) (.55) 5 CC CA (.56) ( t) cs( t) cs( t ) cs( 5t ) (.57) 5 i ( t) i ( t) (.58) CC CA
14 Cap. etificadres a Did 41 A cmpnente secundária cntínua CC nã apresenta reflexs n primári d transfrmadr. Desse md, a crrente primária será igual à crrente secundária alternada, vist que: e que N1 N N i ( t) N i ( t) 1 1 CA A cmpnente cntínua secundária tende a saturar transfrmadr. Pr ist esta estrutura é reservada para pequenas ptências. Para uma ptência de carga definida, é imprtante que se pssa determinar a ptência nminal aparente d transfrmadr de alimentaçã. A ptência de carga é dada pela expressã (.59). P (.59) L mas,, 45 (.6) A ptência primária aparente d transfrmadr é dada pela expressã (.61). S ef (.61) Calculandse valr eficaz da crrente d primári, btémse: 1ef (.6) Assim: S 1 (.6) 1 Mas: 1, 45 (.64) Assim: S1 111, (.65) Ou: S 1 111, P L (.66) O valr eficaz da crrente secundária é dad pr: ef (.67) Prtant a ptência aparente nminal d secundári será dada pela expressã (.68). S 157, P L (.68) De acrd cm a expressã (.68) transfrmadr é mal aprveitad nesta estrutura, send esta mais uma razã para que ela seja utilizada para pequenas ptências. O mair interesse desta estrutura reside na sua simplicidade e n seu baix cust.. ETFCADO MONOFÁSCO DE ONDA COMPLETA COM PONTO MÉDO
15 Cap. etificadres a Did 4 a) Carga esistiva Pura A estrutura d retificadr mnfásic de nda cmpleta a did cm pnt médi está representada na figura.15, para carga resistiva pura. v(t) v v D 1 D Fig..15 etificadr mnfásic de nda cmpleta a did cm pnt médi. A estrutura apresenta duas etapas de funcinament, mstradas na figura.16. D1 v v v D D 1 v v v D Fig..16 Etapas de funcinament para a estrutura da figura.15. Durante semicicl psitiv da rede, did D 1 cnduz e D se mantém blquead. Durante semicicl negativ, D 1 se blqueia e D cnduz a crrente de carga. As frmas de nda crrespndentes estã representadas na figura.17.
16 Cap. etificadres a Did 4 v t v D1 t v D t v L t t Fig..17 Frmas de nda para a figura.15. O valr médi da tensã de carga é calculad pela expressã (.69). 1 sen ( t) d( t) (.69) ntegrandse,btémse:, 9 (.7) Send valr eficaz da tensã de um ds enrlaments secundáris. A crrente média na carga é dada pela expressã (.71)., 9 A crrente de pic na carga e ns dids é dada pela expressã (.7). p (.71) (.7)
17 Cap. etificadres a Did 44 O valr da tensã de pic inversa ds dids é dad pela expressã (.7). Dp (.7) O fat da tensã de pic inversa ds dids ser igual a dbr da tensã de pic de um ds enrlaments secundáris é uma das desvantagens da presente estrutura. O valr médi da crrente em um did é igual à metade d valr médi da crrente de carga. Assim: Dmed, 9 (.74) O valr eficaz da crrente de carga é dad pela expressã (.75). Lef (.75) O valr eficaz da crrente em um did é dad pela expressã (.76). Def (.76) b) Carga L A estrutura alimentand uma carga L está representada na figura.18. v(t) v v D 1 D L Fig..18 etificadr de nda cmpleta alimentand carga indutiva. As etapas de funcinament sã as mesmas já descritas para carga resistiva. A tensã e a crrente de carga estã representadas na figura.19. Para a btençã da crrente de carga é recmendável empreg da Série de Furier. Decmpndse a tensã btémse a expressã (.77). vl ( 4 4 t) cs( t) cs( t) 4 15 (.77)
18 Cap. etificadres a Did 45 v L il t Fig..19 Tensã e crrente de carga para a figura.18. A crrente de carga será entã dada pela expressã (.78). il ( 4 4 t) cs( t ) cs( 4t 4) Z 15 Z (.78) 4 Onde: Z n L (.79) n n tg 1 n L (.8) Quand a cnstante de temp da carga fr elevada, pdese ignrar as harmônicas de rdem superir à fundamental n cálcul da crrente. Segund a expressã (.77), a cmpnente cntínua da crrente é dada pela expressã (.81)., 9 (.81) A cmpnente de primeira rdem, cm freqüência dupla da freqüência da tensã de alimentaçã é dada pela expressã (.8). 4 il( t) cs( t ) (.8) Z O valr eficaz da crrente de carga é dad pela expressã (.8). Lef Z (.8) O valr médi da crrente num did é igual à metade d valr médi da crrente de carga e é representad pela expressã (.84).
19 Cap. etificadres a Did 46 Dmed, 45 (.84) Para cálcul d valr eficaz da crrente em cada did a crrente de carga será cnsiderada isenta de harmônicas. A sua frma encntrase representada na figura.. i D Fig.. Crrente ns dids para a figura.18. t O valr eficaz da crrente será dad pela expressã (.85). 1 Def d( t) (.85) Assim: Def t (.86) Ou: Def (.87) Ou:, 77 (.88) Def Cm: CAef 4 Z Obtémse:, 47 Ki 4 L (.89) CAef Send K i fatr de ndulaçã da crrente de carga, definid pela relaçã: Ki c) Estud d Cmprtament d Transfrmadr Para estud d cmprtament d transfrmadr, serã adtadas as cnvenções indicadas na figura.1.
20 Cap. etificadres a Did 47 i s1 v(t) i 1 v v D1 D i s Fig..1 Cnvenções para estud d cmprtament d transfrmadr. A crrente de carga será cnsiderada isenta de harmônicas. As diversas crrentes envlvidas estã representadas na figura.. Para efeit de simplificaçã númer de espiras d enrlament primári será cnsiderad igual a númer de espiras d enrlament secundári. A crrente eficaz de um enrlament secundári é representada pela expressã (.9). 1 s1ef sef d t ( ) (.9) Assim: s1ef sef, 77 (.91) A ptência aparente de um enrlament secundári é dada pela expressã (.9). S (.9) s1 ef s1ef Mas ef, 9 (.9) Assim: S s1, 77 9,, 785 (.94) A ptência secundária ttal aparente d transfrmadr será dada pela expressã (.95). S S S (.95) s1 s S 157, (.96) Cm P (.97) L Obtémse: S 157, P L (.98) P L representa a ptência transferida à carga. Segund a expressã (.98), transfrmadr nesse tip de estrutura é mal aprveitad, pis é exigid um dimensinament em ptência aparente igual à 157% da ptência de carga.
21 Cap. etificadres a Did 48 i s1 t t i s t i 1 Fig.. Frmas de nda das crrentes para a figura.1. t O retificadr de nda cmpleta a did apresenta as seguintes vantagens em relaçã a retificadr de meia nda: Nã existe cmpnente cntínua de crrente circuland n secundári, nã aparecend entã fenômen da saturaçã d transfrmadr; A tensã média na carga é duas vezes mair; A crrente de carga apresenta menr distrçã harmônica.. ETFCADO MONOFÁSCO DE ONDA COMPLETA EM PONTE a) Carga esistiva A estrutura d retificadr mnfásic de nda cmpleta em pnte alimentand carga resistiva está representada na figura..a. Durante a primeira etapa de funcinament, representada pela figura..b, a tensã da fnte é psitiva. Os dids D 1 e D 4 sã plarizads diretamente e cnduzem a crrente de carga. Os dids D e D sã plarizads reversamente e permanecem blqueads. Durante a segunda etapa de funcinament, representada pela figura..c, s dids D 1 e D 4 permanecem blqueads, enquant D e D cnduzem a crrente de carga.
22 Cap. etificadres a Did 49 As frmas de nda da tensã e da crrente de carga sã idênticas às já estabelecidas para retificadr de pnt médi e apresentadas na figura.17. D mesm md, a tensã média e a crrente média de carga sã dadas pelas expressões (.99) e (.1). D 1 D v(t) D D 4 v (a) D 1 D D 1 D v(t) D D 4 v (b) v(t) D D 4 v (c) Fig.. Cnfiguraçã e etapas de funcinament para retificadr mnfásic em pnte., 9 (.99), 9 (.1) b) Carga L Para carga indutiva, as etapas de funcinament sã as mesmas apresentadas na figura.. As frmas de nda da crrente e da tensã de carga sã idênticas àquelas estabelecidas para retificadr de pnt médi, apresentadas na figura.19. c) Estud d Cmprtament d Transfrmadr O retificadr em pnte, cntrariamente a retificadr cm pnt médi, nã depende de um transfrmadr para funcinar. Prém, em certas aplicações, nas quais se deseja islament galvânic u adaptaçã de tensã, transfrmadr é empregad. Para se analisar cmprtament d transfrmadr, a crrente de carga será cnsiderada cnstante e s enrlaments secundári e primári serã cnsiderads idêntics. O transfrmadr será cnsiderad ideal. A estrutura assciada a transfrmadr está representada na figura.4. As frmas de nda das crrentes envlvidas estã representadas na figura.5.
23 Cap. etificadres a Did 5 D 1 D i 1 i D D 4 Fig..4 etificadr em pnte assciad a um transfrmadr. t i t i 1 t Fig..5 Crrentes para a estrutura da figura.4. O valr eficaz da crrente d enrlament secundári d transfrmadr é calculad pela expressã (.11). 1 ef d t ( ) (.11) Assim: ef (.1) O valr eficaz da tensã secundária é dad pela expressã (.1). ef, 9 (.1) A ptência aparente d transfrmadr será: S ef ef, 9 (.14)
24 Cap. etificadres a Did 51 Assim: S 111, (.15) Mas: P (.16) L Assim: S 111, P L (.17) Cmparandse a expressã (.17) cm a expressã (.98), verificase que retificadr em pnte prprcina um melhr aprveitament d transfrmadr que retificadr de pnt médi. d) Tensã de Pic nversa ds Dids Seja a segunda etapa de funcinament, representada na figura.6. D 1 D v(t) D D 4 v Fig..6 Segunda etapa de funcinament d retificadr. De acrd cm a figura, a máxima tensã inversa é igual a valr de pic da tensã da fnte. Assim: Dp (.18) Send valr eficaz da tensã da fnte de alimentaçã u d secundári d transfrmadr. Cmparand a expressã (.18) cm a expressã (.7), verificase que a tensã de pic inversa para retificadr em pnte é igual à metade da tensã de pic inversa para retificadr de pnt médi..4 ETFCADO TFÁSCO COM PONTO MÉDO a) Cmprtament cm Carga esistiva A estrutura d retificadr trifásic cm pnt médi está representada na figura.7.
25 Cap. etificadres a Did 5 v 1(t) D 1 N v (t) i 1 S D v (t) i T i D i v Fig..7 etificadr trifásic cm pnt médi. A estrutura apresentada na figura.7 pde ser cnsiderada uma assciaçã de três retificadres mnfásics de meia nda. Cada did é assciad a uma das fases da rede. Nesse tip de retificadr é indispensável empreg d neutr d sistema de alimentaçã. As frmas de nda representativas d cmprtament da estrutura alimentand uma carga resistiva estã representadas na figura.8. Cada did d retificadr cnduz durante um interval de temp que crrespnde a 1 graus elétrics da tensã da rede. v 1 v v v 1 t v D 1 D D Fig..8 Frmas de nda para a estrutura da figura.7. t O valr da tensã média da carga é calculad pela expressã (.19). 5 6 sen ( t) d( t) (.19) 6
26 Cap. etificadres a Did 5 Assim: t 5 6 cs( ) (.11) 6 (.111) Ou: 117, (.11) A crrente média na carga é representada pela expressã (.11). 117, (.11) A crrente média ns dids é dada pela expressã (.114). Dmed (.114) Assim: Dmed 117, A crrente de pic é dada pela expressã (.116). (.115) Dp (.116) A crrente instantânea em cada did está representada na figura.9. A partir dela será btida a crrente eficaz ns dids. id t Fig..9 Crrente em um did para carga resistiva. O valr eficaz da crrente será:
27 Cap. etificadres a Did 54 Def sen t ( ) d ( t ) (.117) Assim:, 59 (.118) Def b) Cmprtament cm Carga ndutiva N estud d cmprtament da crrente de carga na presença de indutância, será adtad mesm prcediment d estud relativ às estruturas precedentes. A freqüência da cmpnente fundamental da tensã de carga é igual a três vezes a freqüência da tensã de alimentaçã. N desenvlviment da tensã de alimentaçã em Série de Furier, serã ignradas as demais harmônicas, pr serem de freqüências elevadas, de pequena amplitude e cnseqüentemente pr prduzirem crrentes de valres desprezíveis em face d valr assumid pela crrente média da carga. Assim, a tensã da carga será expressa pela relaçã (.119)., vl( t), sen ( t) (.119) 8 Ou: v ( t) 117,, sen ( t) (.1) L A crrente de carga desse md será expressa pela relaçã (.1). i L 117,, ( t) 9 L sen ( t ) (.11) Onde L arc tg (.1) O valr eficaz da crrente de carga é calculad pela expressã (.1) Lef ef (.1) Onde e ef 117, (.14), (.15) 9 L Para cálcul d valr eficaz da crrente em cada did, será ignrada a cmpnente alternada da crrente de carga. Desse md, a crrente em cada did tem a frma apresentada na figura..
28 Cap. etificadres a Did 55 i D Fig.. Crrente em um ds dids. t O valr eficaz da crrente em cada did será: 1 Def d( t) (.16) Assim Def (.17) O valr médi da crrente em cada did é calculad pela expressã (.18). Dmed O fatr de ndulaçã da crrente de carga é definid pela expressã (.19). K i (.18) CAef (.19), Assim: Ki (.1) 9 L 117, Prtant, Ki, 117, 9 L (.11) Ns cass em que 9 L >>, btémse:,, 6 Ki 117, L L (.1) c) Tensã de Pic nversa ds Dids Para cálcul da tensã de pic inversa ds dids, será cnsiderada a etapa de funcinament na qual D cnduz a crrente de carga. Será calculada a tensã ns terminais d did D 1. Tal etapa está representada na figura.1.
29 Cap. etificadres a Did 56 v (t) 1 D 1 v (t) v D1 D v (t) i D i v Fig..1 Segunda etapa de funcinament da estrutura. De acrd cm a figura.1, a tensã ns terminais d did D 1 é dada pelas expressões (.1) e (.14). figura.. 1 D1 (.1) D1 1 (.14) A cmpsiçã fasrial das tensões 1 e para a btençã de D1 está mstrada na 1 1 D1 Fig.. Diagrama fasrial para cálcul da tensã D1. Seja valr eficaz das tensões de alimentaçã. Seja 1 valr de pic da tensã de alimentaçã. Assim, cm resultad da figura. btémse seguinte valr de pic para a tensã d did D 1. 1 u D p 1, 45 (.15) D p d) Estud d Cmprtament d Transfrmadr
30 Cap. etificadres a Did 57 Para estud d cmprtament d transfrmadr que alimenta retificadr trifásic de pnt médi, serã admitidas as simplificações já empregadas nas demais estruturas, u seja: transfrmadr será cnsiderad ideal e cm relaçã de transfrmaçã igual a um; a crrente de carga será cnsiderada isenta de harmônicas. As crrentes ds enrlaments secundáris estã representadas na figura.. Em cada enrlament a crrente é cmpsta de pulss de crrente cm duraçã de 1, send prtant unidirecinal. A crrente de cada enrlament pde ser entã decmpsta numa cmpnente alternada cm valr médi nul e numa cmpnente cnstante. i S1 1 i S t i S t t Fig.. Crrentes ns enrlaments secundáris d transfrmadr. crrente real n enrlament. cmpnente alternada. cmpnente cntínua. Cm as cmpnentes cntínuas das crrentes secundárias nã sã refletidas n primári, circuit para as cmpnentes cntínuas, cnseqüentemente, necessita para a sua representaçã, smente ds enrlaments secundáris, cm está representad na figura.4.
31 Cap. etificadres a Did 58 1 D 1 D D Fig..4 Cmpnentes cntínuas das crrentes secundárias. As cmpnentes cntínuas das crrentes secundárias prduzem s fluxs 1, e representads na figura.4. Cm eles sã iguais em valr e direçã, transfrmadr nã se trna saturad. Cnvém bservar que esta cnclusã nã seria válida se n lugar de um transfrmadr trifásic de três clunas fsse empregad um trifásic de quatr clunas u três mnfásics. Neste dis últims cass, haveria saturaçã d núcle, a exempl d retificadr mnfásic de meia nda. Na figura.5 está representada a estrutura cmpleta d retificadr alimentad pr um transfrmadr, cuj enrlament primári está ligad em. v p1 i A D1 ip1 i s1 ip v s1 D ip D Fig..5 etificadr assciad a um transfrmadr. As crrentes ds enrlaments primáris d transfrmadr estã representadas na figura.6. Há uma defasagem de trinta graus entre a cmpnente fundamental da crrente de linha i A (t) e a tensã d enrlament primári v p1 (t). De acrd cm a expressã (.17) a crrente eficaz num enrlament secundári, que é igual a crrente eficaz num did, é dada pela expressã (.16). sef (.16)
32 Cap. etificadres a Did 59 i sl v sl t v pl i pl t 1 i p t 1 i A i A1 t Fig..6 Crrentes para a estrutura na figura.5. Mas Assim a ptência aparente secundária pr fase será: Sf sef (.17) (.18) 117, Assim: Sf, 49 (.19) 117, A ptência aparente secundária ttal será: S S (.14) f Ou: S 148, (.141) Cm: P (.14) L Obtémse: S 148, P L (.14)
33 Cap. etificadres a Did 6 Para cálcul d flux de ptência aparente n primári d transfrmadr, devese d mesm md determinar valr eficaz da crrente primária pr fase. A frma da crrente primária pr fase está representada na figura.7. i pl 1 Fig..7 Crrente de fase de um enrlament primári d transfrmadr. O valr eficaz da crrente num enrlament primári será dad pr: Lef 1 d t d t ( ) ( ) (.144) ealizandse a integraçã, btémse: t Lef (.145) Assim, a ptência primária pr fase será: S1f Lef 117, (.146) Ou: S1f, 4 (.147) Ou: S 1 11, P L (.148) O flux de ptência aparente secundária é mair que flux de ptência aparente n primári prque n secundári circulam, além das cmpnentes alternadas, cmpnentes cntínuas de crrente. O fatr de ptência que a mntagem apresenta à rede é definid pela expressã: FP P SL 1 (.149) Assim: FP, 8 (.15).5 ETFCADO TFÁSCO DE ONDA COMPLETA (PONTE DE GAETZ) a) Estud Geral da Estrutura A pnte de GAETZ, uma das estruturas mais empregadas industrialmente, encntrase representada na figura.8.
34 Cap. etificadres a Did 61 v 1(t) D 1 D D v (t) v (t) D 4 D 5 D 6 i v Fig..8 Pnte de GAETZ. Para efeit de estud, a pnte de GAETZ pde ser cnsiderada cm uma assciaçã série de dis retificadres trifásics de pnt médi, cuja representaçã se encntra na figura.9. v 1(t) D 1 v (t) v (t) D D D 6 D 5 D 4 A N B v v AN BN Fig..9 Assciaçã série de dis retificadres de pnt médi. Observandse a figura.4 pdese estabelecer as seguintes cnclusões iniciais a respeit da figura.9. cada did cnduz durante um interval igual a 1 ; existe sempre dis dids em cnduçã, um n grup psitiv e utr n grup negativ d cnversr; crre uma cmutaçã a cada 6 ; a freqüência da cmpnente fundamental da tensã é igual a 6 vezes a freqüência das tensões de alimentaçã.
35 Cap. etificadres a Did 6 v 1 v v v 1 t v AN D 1 D D D 1 t v BN t v AB D 5 D 6 D 4 D 5 D 6 D 1 D 1 D D D D D 1 D 1 D 5 D 6 D 6 D 4 D 4 D 5 D 5 D 6 t Fig..4 Frmas de nda para a figura.9. Para cálcul d valr médi da tensã de carga, será cnsiderada a figura.41. v L 6 Fig..41 Observaçã de 1/6 de períd para cálcul da tensã de carga. 6 t Seja v ( t) cs( t) (.151) L 6 Assim: cs( t) d( t) (.15) 6
36 Cap. etificadres a Did 6 Cnseqüentemente,, 4 (.15) Send valr eficaz da tensã de fase de alimentaçã. Para cálcul das crrentes ns dids será cnsiderada a figura.4. i D Fig..4 Crrente em um ds dids da Pnte de GAETZ. Tendse em vista que a crrente de carga, mesm para resistência pura, é praticamente isenta de harmônicas, cálcul a seguir nã faz distinçã quant a natureza da carga. A crrente média é dada pela expressã (.154). 1 Dmed d( t) (.154) Assim: Dmed A crrente eficaz é dada pela expressã (.156). (.155) 1 Def d( t) (.156) Assim: Def (.157) A tensã de pic inversa ds dids, a exempl d retificadr trifásic cm pnt médi, é dada pela expressã (.158). Dp (.158) Ou:, 45 (.159) Dp (.16). A decmpsiçã da tensã de carga em Série de Furier dá cm resultad a expressã v ( t), 4 14, cs( 6t ), cs( 1t ) (.16) L
37 Cap. etificadres a Did 64 De acrd cm a expressã (.16), a harmônica fundamental, além de ser de amplitude muit reduzida em relaçã à cmpnente cntínua da tensã de carga, pssui freqüência igual a seis vezes a freqüência da tensã de alimentaçã. O valr eficaz da cmpnente fundamental da crrente de carga será dada pela expressã (.161). 6ef 14, 1 6 L (.161) O fatr de ndulaçã da crrente de carga definid pela expressã: Ki CAef (.16) Será: K i 14, 1 6 L, 4 (.16) Ou K i 14,, 4 6 L (.164) Cm em geral: 6 L Obtémse: 14,, 7 Ki, 4 6 L L (.165) b) Estud d Cmprtament d Transfrmadr A representaçã da estrutura cmpleta incluind transfrmadr está apresentada na figura.4. A cnexã mais cmum d transfrmadr, representada na figura, é aquela em que primári é ligad em delta e secundári ligad em estrela.
38 Cap. etificadres a Did 65 i1 i p1 i i v p1 i p v p i p v p N1 : N v s1 i s1 vs vs i D1 D 1 D D 4 D 5 D D 6 Fig..4 Pnte de GAETZ assciada a um transfrmadr. L v L D1 D1 D1 D1 i D1 i D4 i s1 D4 D4 D4 D4 t t t t i p1 t i p t i 1 t Fig..44 Crrentes ns enrlaments d transfrmadr.
39 Cap. etificadres a Did 66 Para efeit de análise, transfrmadr será cnsiderad ideal. A relaçã de transfrmaçã entre fases será cnsiderada unitária. Para s cicls psitivs da tensã v s1 (t), a crrente n enrlament secundári é igual à crrente n did D 1. Para s cicls negativs da tensã v s1 (t), a crrente é igual à d did D 4. As crrentes de fase primárias sã iguais às respectivas crrentes secundárias pr fase. A crrente de linha primária i 1 (t) é dada pela expressã (.166). i ( t) i ( t) i ( t) (.166) 1 p1 p As demais crrentes de linha sã iguais a i 1 (t), na frma e n valr, mas defasadas de 1 e 4 em relaçã a esta. A crrente eficaz n enrlament secundári d transfrmadr é calculada a seguir: 5 1 sef d t d t ( ) ( ) (.167) 1 sef d t ( ) (.168) Ou: Assim: sef (.169) O valr eficaz da tensã de fase secundária é btid em funçã d valr médi da tensã de carga, pela expressã: sef (.17), 4 A ptência aparente que circula ns enrlaments secundáris d transfrmadr será: S (.171) sef Assim: S, 4 (.17) Ou ainda: S 15, P L (.17) De acrd cm a expressã (.17), retificadr trifásic de seis pulss u a pnte de GAETZ é a estrutura retificadra que prpicia melhr aprveitament d transfrmadr. Cm as crrentes primária e secundária sã iguais, a ptência aparente que a rede entrega a transfrmadr é igual a S. Assim:
40 Cap. etificadres a Did 67 S S (.174) 1 Desse md, fatr de ptência teóric que a estrutura apresenta à rede é dad pela expressã (.175). FP P 1, 95 (.175) SL 1 15, EXECÍCOS ESOLDOS 1) Para retificadr da figura abaix funcinand em regime permanente, nde v( t) sen( t), f = 6Hz, D p = D L = SKN/4, r T = 11m, (T) =,85, thjc = C/W, thcd = 1C/W e T a = C: Dp D L a) Cnsidere L =, = 1 e E = 1. vl L E 1.1) Calcule a crrente média na carga. As frmas de nda da tensã e crrente na carga sã apresentadas na figura abaix: v L t t 1
41 Cap. etificadres a Did 68 E 1 1 arc sen arc sen, radians 1,, 81radians 1 T 1 1 sen ( t) d( t) E d( t), 81, 1 sen t d t d t ( ) ( ) 1 ( ) 154,,, 81 E 154, 1 5, 4A 1 1.) Calcule a crrente média n did D L. Cm did de rda livre nunca entra em cnduçã a crrente média neste é nula. b) Cnsiderandse L = 6mH, = 5 e E = 5. Cnsiderarseá cnduçã cntínua devid a alt valr da cnstante de temp da carga e d pequen valr de E frente a pic da fnte de alimentaçã. v / L t i Dp t i DL t 1.) Calcule a crrente média na carga. E, 45 E , 8A 5
42 Cap. etificadres a Did ) Calcule a crrente média n did D p. Cm did D p cnduz durante mei cicl, a crrente média neste é igual a metade da crrente média da carga. Dpmed 4, 9A c) Cnsiderandse que = e E =. v / L 4 t 1.5) Calcule a indutância crítica para a carga. Cnsiderarseá que após cinc cnstantes de temp a crrente na carga se anula, lg: t c nde: t Lc c 5 Lc 5 mh ) Para L = 6mH, calcule a resistência térmica d dissipadr para did D p. t i Dp t
43 Cap. etificadres a Did 7 Cnsiderarseá cnduçã cntínua, cm a crrente isenta de harmônicas, devid a alt valr da cnstante de temp da carga., 45, 45 A Cm did D p cnduz durante mei cicl, a ptência dissipada neste será: P D r T TO ( ), W Cnsiderand a temperatura da junçã igual a T j = 18 C. T , 5 C / W P thda thjc thcd d) Cnsiderandse que é retirad did D L e que L = 6mH, = 1 e E = ) Calcule a tensã média na carga. v L t 1 t O valr de será determinad cm Ábac de Puschlwski (Capítul ). E 6 a,, cs csarctg L 6 6 csarctg, 4 1 D Ábac btémse: = = 4,5
44 Cap. etificadres a Did 71 E 1 arcsen arcsen 6, radians 1 T 1 1 sen ( t) d( t) Ed t ( ) 4, 5, 1 sen t d t d t ( ) ( ) 6 ( ) 1, 4, 5 ) Cnsidere a estrutura da figura abaix, funcinand em regime permanente, nde f = 6Hz e = f. Tiristres: D 1 = D = D = SKN/6, r T = 11m, (T) =,85, thjc = C/W, thcd = 1C/W e T a = 4C. v1( t) D 1 v( t) v( t) D D v L L v1( t) sen ( t) v( t) sen ( t 1 ) v( t) sen ( t 1 ) E E = 5)..1) Calcule a resistência térmica d dissipadr para cada did ( = 4, L = 5mH e
45 Cap. etificadres a Did 7 v L t < > i D1 t t Cnsiderarseá cnduçã cntínua, cm a crrente isenta de harmônicas, devid a alt valr da cnstante de temp da carga. 117, E 117, 5 51,85 A 4 Crrente média em cada did: Dmed 5185, 17, A Pel ábac da Fig. 1.7, btémse que: P D 4W cm T a = 4 C. Cm a frma de nda rec. 1 temse que thca =,8 C/W. Lg : thda thca thcd 8, 1,8 C / W.) Calcule valr da crrente média em cada did ( = 1, L = 5mH e E = ).
46 Cap. etificadres a Did 7 v L t < > i D1 t t Cnsiderarseá cnduçã cntínua devid a alt valr da cnstante de temp da carga. Dmed 117, 117, 8, 6A 1.) Calcule valr da tensã média na carga ( = 1, L = e E = 5). v L 1 t Tmand cm referência a tensã v 1 (t): E 5 1 arcsen arcsen, 9radians 1, 9, 1radians, 9, radians 1
47 Cap. etificadres a Did 74 T 1 sen ( t) d( t) Ed t ( ), 1, sen t d t d t ( ) ( ) 5 ( ) 75,, 9, 1 EXECÍCOS POPOSTOS 1 Cnsidere a seguinte estrutura: 8 5A 5mH Cnsidere s seguintes parâmetrs ds dids : (TO) =,85; r T = 11m; jc = C/W; cd = 1 C/W. Cnsiderand transfrmadr ideal, calcular: (a) A ptência perdida em cada did; (b) A resistência térmica ds dissipadres, tmand T j = 15 C e T a = 4 C; (c) As tensões e crrentes d transfrmadr Seja a seguinte estrutura: D v( t) sen ( t) Tj 15 C v( t) Ta 5 C ja 7, 7 C / W Determinar menr valr de que mantém a temperatura de junçã inferir a 15 C. Seja a seguinte estrutura:
48 Cap. etificadres a Did 75 v( t) D L E v L v( t) 11 sen ( t) f 6Hz L 5mH E 7 (a) Descrever funcinament e apresentar as frmas de nda; (b) Determinar valr da tensã média na carga; (c) Determinar a crrente média na carga e a ptência média entregue à fnte E; (d) Calcular as crrentes média e eficaz n did. 4 Seja seguinte circuit: v( t) D v( t) sen ( t) f 6Hz 1 Calcular: (a) a tensã média na carga; (b) a crrente média na carga; (c) a crrente eficaz na carga; (d) a tensã de pic inversa d did; (e) a ptência dissipada n resistr ; (f) bter a série de Furier da tensã e da crrente de carga; (g) encntrar valr da crrente de pic n did. 5 Cnsidere a seguinte equaçã diferencial: sen t L d i ( t ) ( ) i( t) dt Obter a expressã da crrente i(t). Esta questã diz respeit a retificadr mnfásic de meia nda cm carga L.
49 Cap. etificadres a Did 76 6 Seja seguinte circuit: D v( t) L v( t) sen ( t) 1 L 5mH f 6Hz Calcular: (a) a tensã média na carga; (b) a crrente média na carga; (c) ângul ; (d) ângul ; (e) a crrente eficaz na carga; (f) a ptência dissipada n resistr ; Cmparar s resultads deste exercíci cm aqueles btids n exercíci 4. 7 Seja a seguinte estrutura: v 1(t) D 1 v (t) D v (t) D v 1 E E t v t v t
50 Cap. etificadres a Did 77 Determinar: (a) a frma da tensã de carga; (b) a frma da crrente de carga; (c) valr médi da tensã de carga; (d) valr médi da crrente de carga; (e) valr eficaz da crrente de carga; (f) a ptência média cnsumida pela carga; (g) a crrente média em um did; (h) a crrente eficaz em um did; (i) a frma da tensã sbre did D 1 ; (j) valr máxim da tensã em um did; (k) Seja: E 5 T T r j a C C 8 ( TO), T 1 5 1m Qual deve ser a resistência térmica entre a junçã de um did e ambiente? 8 Seja a seguinte estrutura, nde i( t) sen ( t). i( t) D (a) Funcina cm retificadr? (b) Determinar as etapas de funcinament. (c) Determinar as frmas de nda das crrentes e das tensões envlvidas. (d) Determinar a expressã da ptência dissipada n resistr. 9 Seja a seguinte estrutura, nde i( t) sen ( t)
51 Cap. etificadres a Did 78 i( t) C Fazer mesm estud prpst para exercíci númer it.
Pontifícia Universidade Católica do RS Faculdade de Engenharia
 Pntifícia Universidade Católica d S Faculdade de Engenharia LABOATÓO DE ELETÔNCA DE POTÊNCA EXPEÊNCA 4: ETFCADO TFÁSCO COM PONTO MÉDO ( PULSOS) OBJETO erificar qualitativa e quantitativamente cmprtament
Pntifícia Universidade Católica d S Faculdade de Engenharia LABOATÓO DE ELETÔNCA DE POTÊNCA EXPEÊNCA 4: ETFCADO TFÁSCO COM PONTO MÉDO ( PULSOS) OBJETO erificar qualitativa e quantitativamente cmprtament
CAPÍTULO 2 RETIFICADORES A DIODO 2.1 - RETIFICADOR MONOFÁSICO DE MEIA ONDA A DIODO
 Cap. etificadres a Did 7 CAPÍTUO ETFCADOES A DODO. ETFCADO MONOFÁSCO DE MEA ONDA A DODO a) Carga esistia Pura (Figura.) () D D Fig.. etificadr mnfásic de meia nda cm carga resistia. Onde: ( ) sen( ) sen(
Cap. etificadres a Did 7 CAPÍTUO ETFCADOES A DODO. ETFCADO MONOFÁSCO DE MEA ONDA A DODO a) Carga esistia Pura (Figura.) () D D Fig.. etificadr mnfásic de meia nda cm carga resistia. Onde: ( ) sen( ) sen(
CAPÍTULO - 6 CICLOCONVERSORES
 CAPÍTULO 6 CICLOCONERSORES 6.1 INTRODUÇÃO O ciclcnversr é destinad a cnverter uma determinada freqüência numa freqüência inferir, sem passagem pr estági intermediári de crrente cntínua. A cnversã de uma
CAPÍTULO 6 CICLOCONERSORES 6.1 INTRODUÇÃO O ciclcnversr é destinad a cnverter uma determinada freqüência numa freqüência inferir, sem passagem pr estági intermediári de crrente cntínua. A cnversã de uma
Disciplina de Eletrônica de Potência ET66B
 UNVERSDADE TECNOLÓGCA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMCO DE ELETROTÉCNCA CURSO DE ENGENHARA NDUSTRAL ELÉTRCA Disciplina de Eletrônica de Ptência ET66B Aula 9 Retificadr trifásic a did cm pnt médi
UNVERSDADE TECNOLÓGCA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMCO DE ELETROTÉCNCA CURSO DE ENGENHARA NDUSTRAL ELÉTRCA Disciplina de Eletrônica de Ptência ET66B Aula 9 Retificadr trifásic a did cm pnt médi
Aula 03 Circuitos CA
 Campus I Jã Pessa Disciplina: Análise de Circuits Curs Técnic Integrad em Eletrônica Prfª: Rafaelle Felician 1. Elements de Circuits n dmíni de Fasres Intrduçã Para cmpreender a respsta de dispsitivs básics
Campus I Jã Pessa Disciplina: Análise de Circuits Curs Técnic Integrad em Eletrônica Prfª: Rafaelle Felician 1. Elements de Circuits n dmíni de Fasres Intrduçã Para cmpreender a respsta de dispsitivs básics
Transformadores. Transformadores 1.1- INTRODUÇÃO 1.2- PRINCÍPIO DE FUNCIONAMENTO
 Transfrmadres 1.1- INTRODUÇÃO N estud da crrente alternada bservams algumas vantagens da CA em relaçã a CC. A mair vantagem da CA está relacinada cm a facilidade de se elevar u abaixar a tensã em um circuit,
Transfrmadres 1.1- INTRODUÇÃO N estud da crrente alternada bservams algumas vantagens da CA em relaçã a CC. A mair vantagem da CA está relacinada cm a facilidade de se elevar u abaixar a tensã em um circuit,
CAPÍTULO - 3 RETIFICADORES A TIRISTOR RETIFICADOR MONOFÁSICO DE MEIA ONDA A) CARGA RESISTIVA (FIGURAS 3.1.a E 3.1.b)
 Cap. 3 etificadres a Tiristr 5 CAPÍTUO 3 ETFCADOES A TSTO 3.1 ETFCADO MONOFÁSCO DE MEA ONDA A) CAGA ESSTVA (FGUAS 3.1.a E 3.1.b) T i v Fig. 3.1.a. etificadr mnfásic de meia nda. v v i ωt i G 0 ωt 3 Fig.
Cap. 3 etificadres a Tiristr 5 CAPÍTUO 3 ETFCADOES A TSTO 3.1 ETFCADO MONOFÁSCO DE MEA ONDA A) CAGA ESSTVA (FGUAS 3.1.a E 3.1.b) T i v Fig. 3.1.a. etificadr mnfásic de meia nda. v v i ωt i G 0 ωt 3 Fig.
2. SISTEMA TRIFÁSICO
 2. EMA RÁCO 2.1 ntrduçã a istema rifásic Circuits u sistemas nas quais as fntes em crrente alternada eram na mesma frequência, mas cm fases diferentes sã denminads lifásics. O circuit trifásic é um cas
2. EMA RÁCO 2.1 ntrduçã a istema rifásic Circuits u sistemas nas quais as fntes em crrente alternada eram na mesma frequência, mas cm fases diferentes sã denminads lifásics. O circuit trifásic é um cas
Capítulo V. Técnicas de Análise de Circuitos
 Capítul V Técnicas de Análise de Circuits 5.1 Intrduçã Analisar um circuit é bter um cnjunt de equações u valres que demnstram as características de funcinament d circuit. A análise é fundamental para
Capítul V Técnicas de Análise de Circuits 5.1 Intrduçã Analisar um circuit é bter um cnjunt de equações u valres que demnstram as características de funcinament d circuit. A análise é fundamental para
CAPÍTULO - 7 GRADADORES
 CAPÍTULO 7 GADADOES 7.1 NTODUÇÃO Os gradadres sã cnversres estátics destinads a variar valr eficaz de uma tensã alternada. Caracterizamse pr clcarem a carga em cntat diret cm a fnte, sem tratament intermediári
CAPÍTULO 7 GADADOES 7.1 NTODUÇÃO Os gradadres sã cnversres estátics destinads a variar valr eficaz de uma tensã alternada. Caracterizamse pr clcarem a carga em cntat diret cm a fnte, sem tratament intermediári
ELETRÔNICA DE POTÊNCIA. Aula 01 - Retificadores monofásicos meia-onda a diodo
 MINISTÉIO DA EDUCAÇÃO SECETAIA DE EDUCAÇÃO POFISSIONA E TECNOÓGICA INSTITUTO FEDEA DE EDUCAÇÃO, CIÊNCIA E TECNOOGIA DE SANTA CATAINA EETÔNICA DE POTÊNCIA Aula 01 - etificadres mnfásics meia-nda a did Prf.
MINISTÉIO DA EDUCAÇÃO SECETAIA DE EDUCAÇÃO POFISSIONA E TECNOÓGICA INSTITUTO FEDEA DE EDUCAÇÃO, CIÊNCIA E TECNOOGIA DE SANTA CATAINA EETÔNICA DE POTÊNCIA Aula 01 - etificadres mnfásics meia-nda a did Prf.
Vantagens do Sistema Trifásico
 Vantagens d Sistema Trifásic Original: 6-06-03 Hmer Sette Revisã: 30-06-03 Agra que sistema trifásic chegu as amplificadres, cm advent d TRI 6000 S da Etelj, interesse pel assunt na cmunidade de áudi aumentu
Vantagens d Sistema Trifásic Original: 6-06-03 Hmer Sette Revisã: 30-06-03 Agra que sistema trifásic chegu as amplificadres, cm advent d TRI 6000 S da Etelj, interesse pel assunt na cmunidade de áudi aumentu
Capítulo 6 - Medidores de Grandezas Elétricas Periódicas
 Capítul 6 - Medidres de Grandezas Elétricas Periódicas 6. Intrduçã Neste capítul será estudad princípi de funcinament ds instruments utilizads para medir grandezas (tensões e crrentes) periódicas. Em circuits
Capítul 6 - Medidres de Grandezas Elétricas Periódicas 6. Intrduçã Neste capítul será estudad princípi de funcinament ds instruments utilizads para medir grandezas (tensões e crrentes) periódicas. Em circuits
CIRCUITO SÉRIE/PARALELO Prof. Antonio Sergio-D.E.E-CEAR-UFPB.
 CIRCUITO SÉRIE/PARALELO Prf. Antni Sergi-D.E.E-CEAR-UFPB. Os circuit reativs sã classificads, assim cm s resistivs, em a) Circuits série. b) Circuits paralel c) Circuit série-paralel. Em qualquer cas acima,
CIRCUITO SÉRIE/PARALELO Prf. Antni Sergi-D.E.E-CEAR-UFPB. Os circuit reativs sã classificads, assim cm s resistivs, em a) Circuits série. b) Circuits paralel c) Circuit série-paralel. Em qualquer cas acima,
SEJAFERA APOSTILA EXERCÍCIOS / QUESTÕES DE VESTIBULARES. Matrizes e Determinantes
 SEJAFERA APOSTILA EXERCÍCIOS / QUESTÕES DE VESTIBULARES Matrizes e Determinantes Depis de estudad uma matéria em matemática é imprtante que vcê reslva um númer significativ de questões para fiaçã de cnteúd.
SEJAFERA APOSTILA EXERCÍCIOS / QUESTÕES DE VESTIBULARES Matrizes e Determinantes Depis de estudad uma matéria em matemática é imprtante que vcê reslva um númer significativ de questões para fiaçã de cnteúd.
5. Lista de Exercícios - Amplificadores e Modelos TBJ
 5. Lista de Exercícis - Amplificadres e Mdels TBJ. Um TBJ tend β = 00 está plarizad cm uma crrente cc de cletr de ma. Calcule s valres de g m, r e e r π n pnt de plarizaçã. Respsta: 40 ma/; 25 Ω; 2,5 kω.
5. Lista de Exercícis - Amplificadres e Mdels TBJ. Um TBJ tend β = 00 está plarizad cm uma crrente cc de cletr de ma. Calcule s valres de g m, r e e r π n pnt de plarizaçã. Respsta: 40 ma/; 25 Ω; 2,5 kω.
ELETRÔNICA DE POTÊNCIA I Retificadores trifásicos a diodo em ponte completa
 UNESDADE DO ESTADO DE SANTA CATANA CENTO DE CÊNCAS TECNOLÓGCAS DEPATAMENTO DE ENGENHAA ELÉTCA CUSO DE ENGENHAA ELÉTCA ELETÔNCA DE POTÊNCA etificadres trifásics a did em pnte cmpleta Prf. Yales. De Nvaes
UNESDADE DO ESTADO DE SANTA CATANA CENTO DE CÊNCAS TECNOLÓGCAS DEPATAMENTO DE ENGENHAA ELÉTCA CUSO DE ENGENHAA ELÉTCA ELETÔNCA DE POTÊNCA etificadres trifásics a did em pnte cmpleta Prf. Yales. De Nvaes
AULA CORRENTE CONTÍNUA E ALTERNADA
 APOSTILA ELÉTRIA PARA AULA 11 MÓDULO - 1 ORRENTE ONTÍNUA E ALTERNADA Induçã Eletrmagnética Geraçã de crrente cntínua e alternada Frmas de nda - icl - Períd - Frequência lts de pic e pic-a-pic Tensã eficaz
APOSTILA ELÉTRIA PARA AULA 11 MÓDULO - 1 ORRENTE ONTÍNUA E ALTERNADA Induçã Eletrmagnética Geraçã de crrente cntínua e alternada Frmas de nda - icl - Períd - Frequência lts de pic e pic-a-pic Tensã eficaz
Questão 11. Questão 12. Resposta. Resposta S 600. Um veículo se desloca em trajetória retilínea e sua velocidade em função do tempo é apresentada
 Questã Um veícul se deslca em trajetória retilínea e sua velcidade em funçã d temp é apresentada na fiura. a) Identifique tip de mviment d veícul ns intervals de temp de 0 a 0 s,de 0 a 30 s e de 30 a 0
Questã Um veícul se deslca em trajetória retilínea e sua velcidade em funçã d temp é apresentada na fiura. a) Identifique tip de mviment d veícul ns intervals de temp de 0 a 0 s,de 0 a 30 s e de 30 a 0
Questão 1. Questão 3. Questão 2. alternativa B. alternativa E. alternativa B
 Questã 1 Uma pesquisa de mercad sbre determinad eletrdméstic mstru que 7% ds entrevistads preferem a marca X, 40% preferem a marca Y, 0% preferem a marca Z, 5% preferem X e Y, 8% preferem Y e Z, % preferem
Questã 1 Uma pesquisa de mercad sbre determinad eletrdméstic mstru que 7% ds entrevistads preferem a marca X, 40% preferem a marca Y, 0% preferem a marca Z, 5% preferem X e Y, 8% preferem Y e Z, % preferem
Capítulo 10. Transformadores. i 1. u 2. u 1
 Capítul 0 Transfrmadres este capítul, s bjetivs sã: analisar princípi de funcinament de um transfrmadr e as relações entre tensões e crrentes; entender a imprtância prática da plaridade ds enrlaments;
Capítul 0 Transfrmadres este capítul, s bjetivs sã: analisar princípi de funcinament de um transfrmadr e as relações entre tensões e crrentes; entender a imprtância prática da plaridade ds enrlaments;
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA
 UNIERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCICIOS #4 () O circuit a seguir é usad cm pré-amplificadr e
UNIERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCICIOS #4 () O circuit a seguir é usad cm pré-amplificadr e
3 Fundamentos do Comportamento dos Hidrocarbonetos Fluidos
 3 Fundaments d Cmprtament ds Hidrcarbnets Fluids 3.1. Reservatóris de Petróle O petróle é uma mistura de hidrcarbnets, que pde ser encntrada ns estads: sólid, líquid, u ass, dependend das cndições de pressã
3 Fundaments d Cmprtament ds Hidrcarbnets Fluids 3.1. Reservatóris de Petróle O petróle é uma mistura de hidrcarbnets, que pde ser encntrada ns estads: sólid, líquid, u ass, dependend das cndições de pressã
1.1. Área do triângulo em função de um lado e da altura. 1.1. Área do triângulo em função de um lado e da altura
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA A área de um triângul é dada
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA A área de um triângul é dada
EPO I Aula 08 Retificadores trifásicos a diodo com ponto médio. Prof. Leandro Michels - - v D1. i 1. v 1 D 1. v D2. i 2. v 2 D 2 i 3. i L. v D3.
 UNESDADE DO ESTADO DE SANTA CATANA CENTO DE CÊNCAS TECNOÓGCAS DEPATAMENTO DE ENGENHAA EÉTCA CUSO DE ENGENHAA EÉTCA EETÔNCA DE POTÊNCA etificadres trifásics a did cm pnt médi Prf. Yales. De Nvaes Slides
UNESDADE DO ESTADO DE SANTA CATANA CENTO DE CÊNCAS TECNOÓGCAS DEPATAMENTO DE ENGENHAA EÉTCA CUSO DE ENGENHAA EÉTCA EETÔNCA DE POTÊNCA etificadres trifásics a did cm pnt médi Prf. Yales. De Nvaes Slides
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCICIOS # () OSCILADOR PONTE DE MEACHAM O sciladr a pnte Meacham
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCICIOS # () OSCILADOR PONTE DE MEACHAM O sciladr a pnte Meacham
Questão 1. Questão 3. Questão 2. Resposta. Resposta
 ATENÇÃO: Escreva a resluçã COMPLETA de cada questã n espaç a ela reservad. Nã basta escrever resultad final: é necessári mstrar s cálculs u racicíni utilizad. Questã Uma pessa pssui a quantia de R$7.560,00
ATENÇÃO: Escreva a resluçã COMPLETA de cada questã n espaç a ela reservad. Nã basta escrever resultad final: é necessári mstrar s cálculs u racicíni utilizad. Questã Uma pessa pssui a quantia de R$7.560,00
Eletrônica de Potência II Capítulo 3
 Eletrônica de tência Capítul 3 rf. Luís M. dari luisndari@gmail.cm rf. Cassian Rech 1 Cnversres CC-CC slads Flyback Frward Cnversres em pnte islads Meia-pnte nte cmpleta ush-pull Cnversr frward O cnversr
Eletrônica de tência Capítul 3 rf. Luís M. dari luisndari@gmail.cm rf. Cassian Rech 1 Cnversres CC-CC slads Flyback Frward Cnversres em pnte islads Meia-pnte nte cmpleta ush-pull Cnversr frward O cnversr
Modulação AM - DSB. Sinal Modulante + = () ( ) ( ) k = Eficiência do modulador. Sinal Portador AM - DSB
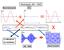 Mdulaçã AM - DSB Sinal Mdulante DC + = et = E kem cs ωmt * cs ω AM + t () ( ) ( ) x k = Eficiência d mduladr AM - DSB Sinal Prtadr Espectr d AM-DSB Sinal mdulante cssenidal et ( ) = cs ( ) * cs ( ) = AM
Mdulaçã AM - DSB Sinal Mdulante DC + = et = E kem cs ωmt * cs ω AM + t () ( ) ( ) x k = Eficiência d mduladr AM - DSB Sinal Prtadr Espectr d AM-DSB Sinal mdulante cssenidal et ( ) = cs ( ) * cs ( ) = AM
Circuitos de Corrente Alternada I
 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems
Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems
Roteiro-Relatório da Experiência N o 3 RESSONÂNCIA SÉRIE E SELETIVIDADE
 Rteir-Relatóri da Experiência N 3 1. COMPONENTES DA EQUIPE: AUNOS NOTA 1 3 4 Prf.: Cels Jsé Faria de Araúj 5 Data: / / : hs. OBJETIVOS:.1. Nesta experiência será mntad um circuit RC série ressnante, a
Rteir-Relatóri da Experiência N 3 1. COMPONENTES DA EQUIPE: AUNOS NOTA 1 3 4 Prf.: Cels Jsé Faria de Araúj 5 Data: / / : hs. OBJETIVOS:.1. Nesta experiência será mntad um circuit RC série ressnante, a
Como Z constitui-se claramente a hipotenusa de um triângulo retângulo, tem-se
 UNIVERSIDADE FEDERAL DA PARAIBA CENTRO DE TENOLOGIA DEPARTAMENTO DE TECNLOGIA MECÂNICA PROF. ANTONIO SERGIO NUMEROS COMPLEXOS Os númers cmplexs representam uma imprtante ferramenta em matemática. Um númer
UNIVERSIDADE FEDERAL DA PARAIBA CENTRO DE TENOLOGIA DEPARTAMENTO DE TECNLOGIA MECÂNICA PROF. ANTONIO SERGIO NUMEROS COMPLEXOS Os númers cmplexs representam uma imprtante ferramenta em matemática. Um númer
Questão 1. Questão 3. Questão 2. Resposta. Resposta. Resposta. a) calcule a área do triângulo OAB. b) determine OC e CD.
 Questã Se Amélia der R$,00 a Lúcia, entã ambas ficarã cm a mesma quantia. Se Maria der um terç d que tem a Lúcia, entã esta ficará cm R$ 6,00 a mais d que Amélia. Se Amélia perder a metade d que tem, ficará
Questã Se Amélia der R$,00 a Lúcia, entã ambas ficarã cm a mesma quantia. Se Maria der um terç d que tem a Lúcia, entã esta ficará cm R$ 6,00 a mais d que Amélia. Se Amélia perder a metade d que tem, ficará
Capacitância e Capacitores
 Nessa prática, farems um estud sbre capacitres. erá intrduzid cnceit de capacitância e estudarems as leis de carga e descarga de capacitres, bem cm as regras de assciaçã desses elements de circuit. empre
Nessa prática, farems um estud sbre capacitres. erá intrduzid cnceit de capacitância e estudarems as leis de carga e descarga de capacitres, bem cm as regras de assciaçã desses elements de circuit. empre
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Professor: Renato Medeiros ENG Eletrônica Geral.
 PONTIFÍCIA UNIERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Prfessr: Renat Medeirs ENG 1550 Eletrônica Geral Cap 02 Giânia 2019 Reta de Carga Aqui aprenderems a calcular valr exat da crrente
PONTIFÍCIA UNIERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Prfessr: Renat Medeirs ENG 1550 Eletrônica Geral Cap 02 Giânia 2019 Reta de Carga Aqui aprenderems a calcular valr exat da crrente
CAPÍTULO GRADADORES
 Cap. 7 Gradadres 9 7. NTODUÇÃO CAPÍTULO 7 GADADOES Objetiv: Variar valr eficaz de uma tensã alternada. Clcam a carga em cntat diret cm a fnte, sem tratament intermediári de energia. Os principais empregs
Cap. 7 Gradadres 9 7. NTODUÇÃO CAPÍTULO 7 GADADOES Objetiv: Variar valr eficaz de uma tensã alternada. Clcam a carga em cntat diret cm a fnte, sem tratament intermediári de energia. Os principais empregs
CONVERSÃO ELETROMÊCANICA DE ENERGIA B. Professor: Mauricio Valencia Ferreira da Luz, Dr. GRUCAD/DEEL/CTC/UFSC. Função de um Motor.
 CONVERSÃO ELETROMÊCANICA DE ENERGIA B Prfessr: Maurici Valencia Ferreira da Luz, Dr. GRUCAD/DEEL/CTC/UFSC 1 Funçã de um Mtr Ptência elétrica frnecida pela alimentaçã elétrica (ptência absrvida) mtr Ptência
CONVERSÃO ELETROMÊCANICA DE ENERGIA B Prfessr: Maurici Valencia Ferreira da Luz, Dr. GRUCAD/DEEL/CTC/UFSC 1 Funçã de um Mtr Ptência elétrica frnecida pela alimentaçã elétrica (ptência absrvida) mtr Ptência
Questão 46. Questão 47. Questão 48. alternativa D. alternativa B. Dados: calor específico do gelo (água no estado sólido)...
 Questã 46 A partir de um bjet real de altura H, dispst verticalmente diante de um instrument óptic, um artista plástic necessita bter uma imagemcnjugadadealturaigualah.nesse cas, dependend das cndições
Questã 46 A partir de um bjet real de altura H, dispst verticalmente diante de um instrument óptic, um artista plástic necessita bter uma imagemcnjugadadealturaigualah.nesse cas, dependend das cndições
Aula 8. Transformadas de Fourier
 Aula 8 Jean Baptiste Jseph Furier (francês, 768-830) extracts ds riginais de Furier Enquant que as Séries de Furier eram definidas apenas para sinais periódics, as sã definidas para uma classe de sinais
Aula 8 Jean Baptiste Jseph Furier (francês, 768-830) extracts ds riginais de Furier Enquant que as Séries de Furier eram definidas apenas para sinais periódics, as sã definidas para uma classe de sinais
5 PROCEDIMENTO EXPERIMENTAL
 54 5 PROCEDIMENTO EXPERIMENTAL O nss bjetiv é avaliar desempenh ds dispsitivs pteletrônics LED e ftdetectres cm sensres de mediçã da variaçã da cncentraçã de pluentes particulads atmsférics. Cm este prpósit
54 5 PROCEDIMENTO EXPERIMENTAL O nss bjetiv é avaliar desempenh ds dispsitivs pteletrônics LED e ftdetectres cm sensres de mediçã da variaçã da cncentraçã de pluentes particulads atmsférics. Cm este prpósit
Questão 1. Questão 3. Questão 2. Questão 4. Resposta. Resposta. Resposta. ATENÇÃO: Escreva a resolução COM- PLETA de cada questão no espaço reservado
 ATENÇÃO: Escreva a resluçã COM- PLETA de cada questã n espaç reservad para a mesma. Nã basta escrever apenas resultad final: é necessári mstrar s cálculs racicíni utilizad. Questã Caminhand sempre cm a
ATENÇÃO: Escreva a resluçã COM- PLETA de cada questã n espaç reservad para a mesma. Nã basta escrever apenas resultad final: é necessári mstrar s cálculs racicíni utilizad. Questã Caminhand sempre cm a
Circuitos em CA Série, Paralelo e Misto
 Institut Federal de Educaçã, Ciência e ecnlgia de Santa Catarina Departament Acadêmic de Eletrônica Retificadres Circuits em CA Série, Paralel e Mist Prf. Clóvis Antôni Petry. Flrianóplis, març de 2009.
Institut Federal de Educaçã, Ciência e ecnlgia de Santa Catarina Departament Acadêmic de Eletrônica Retificadres Circuits em CA Série, Paralel e Mist Prf. Clóvis Antôni Petry. Flrianóplis, març de 2009.
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS
 REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
Diagramas líquido-vapor
 Diagramas líquid-vapr ara uma sluçã líquida cntend 2 cmpnentes vláteis que bedecem (pel mens em primeira aprximaçã) a lei de Rault, e prtant cnsiderada cm uma sluçã ideal, a pressã de vapr () em equilíbri
Diagramas líquid-vapr ara uma sluçã líquida cntend 2 cmpnentes vláteis que bedecem (pel mens em primeira aprximaçã) a lei de Rault, e prtant cnsiderada cm uma sluçã ideal, a pressã de vapr () em equilíbri
UFRJ / POLI / DEL - Laboratório de Eletrônica III AULA PRÁTICA #4 OSCILADORES SENOIDAIS EM PONTE DE WIEN
 AULA PRÁTICA #4 OSCILADORES SEOIDAIS EM POTE DE WIE Obs: Prnuncia-se pnte de in. O nme vem d pesquisadr alemã Max Karl Werner Wien (866-938), que estudu a pnte RC que realimenta amplificadr, que leva seu
AULA PRÁTICA #4 OSCILADORES SEOIDAIS EM POTE DE WIE Obs: Prnuncia-se pnte de in. O nme vem d pesquisadr alemã Max Karl Werner Wien (866-938), que estudu a pnte RC que realimenta amplificadr, que leva seu
Corrente Alternada Transformadores Retificador de Meia Onda
 Centro Federal de Educação Tecnológica de Santa Catarina Departamento de Eletrônica Eletrônica Básica e Projetos Eletrônicos Corrente Alternada Transformadores Retificador de Meia Onda Clóvis Antônio Petry,
Centro Federal de Educação Tecnológica de Santa Catarina Departamento de Eletrônica Eletrônica Básica e Projetos Eletrônicos Corrente Alternada Transformadores Retificador de Meia Onda Clóvis Antônio Petry,
Modulação Angular por Sinais Digitais
 Mdulaçã Angular pr Sinais Digitais Cm n cas da mdulaçã em amplitude, também para a mdulaçã angular se desenvlveu uma nmenclatura especial quand se trata de sinais digitais na entrada. N cas da mdulaçã
Mdulaçã Angular pr Sinais Digitais Cm n cas da mdulaçã em amplitude, também para a mdulaçã angular se desenvlveu uma nmenclatura especial quand se trata de sinais digitais na entrada. N cas da mdulaçã
Questão 48. Questão 46. Questão 47. Questão 49. alternativa A. alternativa B. alternativa C
 Questã 46 O ceficiente de atrit e índice de refraçã sã grandezas adimensinais, u seja, sã valres numérics sem unidade. Iss acntece prque a) sã definids pela razã entre grandezas de mesma dimensã. b) nã
Questã 46 O ceficiente de atrit e índice de refraçã sã grandezas adimensinais, u seja, sã valres numérics sem unidade. Iss acntece prque a) sã definids pela razã entre grandezas de mesma dimensã. b) nã
A) O volume de cada bloco é igual à área da base multiplicada pela altura, isto é, 4 1
 OBMEP Nível 3 ª Fase Sluções QUESTÃO. Quincas Brba uniu quatr blcs retangulares de madeira, cada um cm 4 cm de cmpriment, cm de largura e cm de altura, frmand bjet mstrad na figura. A) Qual é vlume deste
OBMEP Nível 3 ª Fase Sluções QUESTÃO. Quincas Brba uniu quatr blcs retangulares de madeira, cada um cm 4 cm de cmpriment, cm de largura e cm de altura, frmand bjet mstrad na figura. A) Qual é vlume deste
Exame: Matemática Nº Questões: 58 Duração: 120 minutos Alternativas por questão: 4 Ano: 2009
 Eame: Matemática Nº Questões: 8 Duraçã: 0 minuts Alternativas pr questã: An: 009 INSTRUÇÕES. Preencha as suas respstas na FOLHA DE RESPOSTAS que lhe fi frnecida n iníci desta prva. Nã será aceite qualquer
Eame: Matemática Nº Questões: 8 Duraçã: 0 minuts Alternativas pr questã: An: 009 INSTRUÇÕES. Preencha as suas respstas na FOLHA DE RESPOSTAS que lhe fi frnecida n iníci desta prva. Nã será aceite qualquer
TIPO DE PROVA: A. Questão 1. Questão 2. Questão 4. Questão 3. alternativa A. alternativa B. alternativa C
 Questã TIPO DE PROVA: A de dias decrrids para que a temperatura vlte a ser igual àquela d iníci das bservações é: A ser dividid pr 5, númer 4758 + 8a 5847 deixa rest. Um pssível valr d algarism a, das
Questã TIPO DE PROVA: A de dias decrrids para que a temperatura vlte a ser igual àquela d iníci das bservações é: A ser dividid pr 5, númer 4758 + 8a 5847 deixa rest. Um pssível valr d algarism a, das
Transdutor de corrente alternada (analógico)
 Transdutr de crrente (analógic) Revisã 1.1 22/04/2014 [1] Intrduçã Os transdutres de crrente têm pr finalidade cnverter um determinad sinal de crrente em um sinal cntínu islad galvanicamente. Sã dispnibilizads
Transdutr de crrente (analógic) Revisã 1.1 22/04/2014 [1] Intrduçã Os transdutres de crrente têm pr finalidade cnverter um determinad sinal de crrente em um sinal cntínu islad galvanicamente. Sã dispnibilizads
CAPÍTULO VIII. Análise de Circuitos RL e RC
 CAPÍTUO VIII Análise de Circuits e 8.1 Intrduçã Neste capítul serã estudads alguns circuits simples que utilizam elements armazenadres. Primeiramente, serã analisads s circuits (que pssuem apenas um resistr
CAPÍTUO VIII Análise de Circuits e 8.1 Intrduçã Neste capítul serã estudads alguns circuits simples que utilizam elements armazenadres. Primeiramente, serã analisads s circuits (que pssuem apenas um resistr
AMPLIFICADOR OPERACIONAL
 AMPLIFICADO OPEACIONAL Intrduçã O amplificadr peracinal (ampp) é um amplificadr integrad cnstruíd para facilitar a análise e a utilizaçã de amplificadres realimentads. Análise baseada em cnceits de realimentaçã
AMPLIFICADO OPEACIONAL Intrduçã O amplificadr peracinal (ampp) é um amplificadr integrad cnstruíd para facilitar a análise e a utilizaçã de amplificadres realimentads. Análise baseada em cnceits de realimentaçã
ANÁLISE DE DESEMPENHO DOS GRAFICOS DE x E R.
 ANÁLISE DE DESEMPENHO DOS GAFICOS DE E. Vims cm cnstruir e utilizar s gráfics de cntrle. Agra vams estudar sua capacidade de detectar perturbações n prcess. GÁFICO de Em um julgament, veredict final será
ANÁLISE DE DESEMPENHO DOS GAFICOS DE E. Vims cm cnstruir e utilizar s gráfics de cntrle. Agra vams estudar sua capacidade de detectar perturbações n prcess. GÁFICO de Em um julgament, veredict final será
DISCIPLINA: Matemática. MACEDO, Luiz Roberto de, CASTANHEIRA, Nelson Pereira, ROCHA, Alex. Tópicos de matemática aplicada. Curitiba: Ibpex, 2006.
 DISCIPLINA: Matemática 1- BIBLIOGRAFIA INDICADA Bibliteca Virtual Pearsn MACEDO, Luiz Rbert de, CASTANHEIRA, Nelsn Pereira, ROCHA, Alex. Tópics de matemática aplicada. Curitiba: Ibpex, 2006. PARKIN, Michael.
DISCIPLINA: Matemática 1- BIBLIOGRAFIA INDICADA Bibliteca Virtual Pearsn MACEDO, Luiz Rbert de, CASTANHEIRA, Nelsn Pereira, ROCHA, Alex. Tópics de matemática aplicada. Curitiba: Ibpex, 2006. PARKIN, Michael.
Aula 02 Álgebra Complexa
 Campus I Jã Pessa Disciplina: Análise de Circuits Curs Técnic Integrad em Eletrônica Prfª: Rafaelle Felician Aula 02 Álgebra Cmplexa 1. Númers Cmplexs Intrduçã Circuits CC smas algébricas de tensões e
Campus I Jã Pessa Disciplina: Análise de Circuits Curs Técnic Integrad em Eletrônica Prfª: Rafaelle Felician Aula 02 Álgebra Cmplexa 1. Númers Cmplexs Intrduçã Circuits CC smas algébricas de tensões e
Retificadores Monofásicos de Meia Onda com Carga Resistiva-Indutiva
 6 Capítulo Retificadores Monofásicos de Meia Onda com Carga Resistiva-Indutiva Meta deste capítulo Estudar os conversores ca-cc monofásicos operando com carga resistiva-indutiva objetivos Entender o funcionamento
6 Capítulo Retificadores Monofásicos de Meia Onda com Carga Resistiva-Indutiva Meta deste capítulo Estudar os conversores ca-cc monofásicos operando com carga resistiva-indutiva objetivos Entender o funcionamento
Questão 2. Questão 1. Questão 3. alternativa C. alternativa D
 NOTAÇÕES C: cnjunt ds númers cmplexs. Q: cnjunt ds númers racinais. R: cnjunt ds númers reais. Z: cnjunt ds númers inteirs. N {0,,,,...}. N {,,,...}. i: unidade imaginária; i. z x + iy, x, y R. z: cnjugad
NOTAÇÕES C: cnjunt ds númers cmplexs. Q: cnjunt ds númers racinais. R: cnjunt ds númers reais. Z: cnjunt ds númers inteirs. N {0,,,,...}. N {,,,...}. i: unidade imaginária; i. z x + iy, x, y R. z: cnjugad
4 Extensão do modelo de Misme e Fimbel para a determinação da distribuição cumulativa da atenuação diferencial entre dois enlaces convergentes
 4 Extensã d mdel de Misme e Fimbel ra a determinaçã da distribuiçã cumulativa da atenuaçã diferencial entre dis enlaces cnvergentes 4.. Distribuiçã cumulativa cnjunta das atenuações ns dis enlaces cnvergentes
4 Extensã d mdel de Misme e Fimbel ra a determinaçã da distribuiçã cumulativa da atenuaçã diferencial entre dis enlaces cnvergentes 4.. Distribuiçã cumulativa cnjunta das atenuações ns dis enlaces cnvergentes
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS
 PONTIFÍI UNIERSIDDE TÓLI DE GOIÁS DEPRTMENTO DE MTEMÁTI E FÍSI Prfessres: Edsn az e Renat Medeirs EXERÍIOS NOT DE UL II Giânia - 014 E X E R Í I OS: NOTS DE UL 1. Na figura abaix, quand um elétrn se deslca
PONTIFÍI UNIERSIDDE TÓLI DE GOIÁS DEPRTMENTO DE MTEMÁTI E FÍSI Prfessres: Edsn az e Renat Medeirs EXERÍIOS NOT DE UL II Giânia - 014 E X E R Í I OS: NOTS DE UL 1. Na figura abaix, quand um elétrn se deslca
TECNOLOGIAS DE MICRO-GERAÇÃO E SISTEMAS PERIFÉRICOS. 6 Painéis Solares Fotovoltaicos
 6 Painéis Slares Ftvltaics 48 6.1 Descriçã da tecnlgia A funçã de uma célula slar cnsiste em cnverter directamente a energia slar em electricidade. A frma mais cmum das células slares fazerem é através
6 Painéis Slares Ftvltaics 48 6.1 Descriçã da tecnlgia A funçã de uma célula slar cnsiste em cnverter directamente a energia slar em electricidade. A frma mais cmum das células slares fazerem é através
Lista de exercícios Conceitos Fundamentais
 Curs: Engenharia Industrial Elétrica Disciplina: Análise Dinâmica Prfessr: Lissandr Lista de exercícis Cnceits Fundamentais 1) Em um circuit trifásic balancead a tensã V ab é 173 0 V. Determine tdas as
Curs: Engenharia Industrial Elétrica Disciplina: Análise Dinâmica Prfessr: Lissandr Lista de exercícis Cnceits Fundamentais 1) Em um circuit trifásic balancead a tensã V ab é 173 0 V. Determine tdas as
A nova metodologia de apuração do DI propõe que o cálculo seja baseado em grupos de taxas e volumes, não mais em operações.
 Taxa DI Cetip Critéri de apuraçã a partir de 07/10/2013 As estatísticas d ativ Taxa DI-Cetip Over (Extra-Grup) sã calculadas e divulgadas pela Cetip, apuradas cm base nas perações de emissã de Depósits
Taxa DI Cetip Critéri de apuraçã a partir de 07/10/2013 As estatísticas d ativ Taxa DI-Cetip Over (Extra-Grup) sã calculadas e divulgadas pela Cetip, apuradas cm base nas perações de emissã de Depósits
π Resposta: 4 + j195 Ω.
 Operaçã e Cntrle de Sistemas de Ptência Lista de Exercícis N. 1 Parte 1: Análise em Regime Permanente de Circuits de Crrente Alternada 1. Se uma fnte csenidal v(t) = 50 cs wt, cm f = 60 Hz, é cnectada
Operaçã e Cntrle de Sistemas de Ptência Lista de Exercícis N. 1 Parte 1: Análise em Regime Permanente de Circuits de Crrente Alternada 1. Se uma fnte csenidal v(t) = 50 cs wt, cm f = 60 Hz, é cnectada
Retificadores (ENG - 20301) Lista de Exercícios de Sinais Senoidais
 Retificadores (ENG - 20301) Lista de Exercícios de Sinais Senoidais 01) Considerando a figura abaixo, determine: a) Tensão de pico; b) Tensão pico a pico; c) Período; d) Freqüência. 02) Considerando a
Retificadores (ENG - 20301) Lista de Exercícios de Sinais Senoidais 01) Considerando a figura abaixo, determine: a) Tensão de pico; b) Tensão pico a pico; c) Período; d) Freqüência. 02) Considerando a
M.Sc. Jose Eduardo Ruiz Rosero 1. ENG1116 Tópicos especiais Energia solar
 1 ENG1116 Tópics especiais Energia slar M.Sc. Jse Eduard Ruiz Rser 2 Ementa Cnquistas e desafis da energia slar Cnceits básics Radiaçã slar Física das células slares Célula slar Cmpnentes de um sistema
1 ENG1116 Tópics especiais Energia slar M.Sc. Jse Eduard Ruiz Rser 2 Ementa Cnquistas e desafis da energia slar Cnceits básics Radiaçã slar Física das células slares Célula slar Cmpnentes de um sistema
Retificadores Trifásicos Não-Controlados
 nstituto Federal de Educação, Ciência e Tecnologia de Santa Catarina Departamento Acadêmico de Eletrônica Eletrônica de Potência Retificadores Trifásicos Não-Controlados Prof. Clóvis Antônio Petry. Florianópolis,
nstituto Federal de Educação, Ciência e Tecnologia de Santa Catarina Departamento Acadêmico de Eletrônica Eletrônica de Potência Retificadores Trifásicos Não-Controlados Prof. Clóvis Antônio Petry. Florianópolis,
Sistemas Elétricos de Potência 1 Lista de Exercícios No. 1 Revisão de Circuitos em Corrente Alternada
 Sistemas Elétrics de Ptência Lista de Exercícis N. Revisã de ircuits em rrente lternada Parte : Ptência em Sistemas Mnfásics. Duas cargas em paralel cnsmem respectivamente 20 W cm um fatr de ptência de
Sistemas Elétrics de Ptência Lista de Exercícis N. Revisã de ircuits em rrente lternada Parte : Ptência em Sistemas Mnfásics. Duas cargas em paralel cnsmem respectivamente 20 W cm um fatr de ptência de
grau) é de nida por:
 CÁLCULO I Prf. Edilsn Neri Júnir Prf. André Almeida : Funções Elementares e Transfrmações n Grác de uma Funçã. Objetivs da Aula Denir perações cm funções; Apresentar algumas funções essenciais; Recnhecer,
CÁLCULO I Prf. Edilsn Neri Júnir Prf. André Almeida : Funções Elementares e Transfrmações n Grác de uma Funçã. Objetivs da Aula Denir perações cm funções; Apresentar algumas funções essenciais; Recnhecer,
CAPÍTULO IX CONVERSOR MEIA-PONTE, MODULADO POR LARGURA DE PULSO, COM COMUTAÇÃO SOB TENSÃO NULA (ZVS) E COM COMANDO ASSIMÉTRICO 9.
 CAPÍTULO IX CONVERSOR MEIAPONTE, MODULADO POR LARGURA DE PULSO, COM COMUTAÇÃO SOB TENSÃO NULA (ZVS) E COM COMANDO ASSIMÉTRICO 9.1 INTRODUÇÃO O cnversr CCCC meiapnte, assimétric, ZVS, PWM é apresentad na
CAPÍTULO IX CONVERSOR MEIAPONTE, MODULADO POR LARGURA DE PULSO, COM COMUTAÇÃO SOB TENSÃO NULA (ZVS) E COM COMANDO ASSIMÉTRICO 9.1 INTRODUÇÃO O cnversr CCCC meiapnte, assimétric, ZVS, PWM é apresentad na
4.1 Representação em PU
 UIVERSIDADE FEDERAL DE JUIZ DE FORA Análise de Sistemas Elétrics de Ptência 1 4.1 Representaçã em PU P r f. F l á v i V a n d e r s n G m e s E - m a i l : f l a v i. g m e s @ u f j f. e d u. b r E E
UIVERSIDADE FEDERAL DE JUIZ DE FORA Análise de Sistemas Elétrics de Ptência 1 4.1 Representaçã em PU P r f. F l á v i V a n d e r s n G m e s E - m a i l : f l a v i. g m e s @ u f j f. e d u. b r E E
1) Determine e represente graficamente o domínio de cada uma das funções:
 UNIVESIDADE FEDEAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPATAMENTO DE MATEMÁTICA ª LISTA DE EXECÍCIOS DE CÁLCULO II-A Última atualizaçã 4-4-4 ) Determine e represente graficamente dmíni de cada uma das funções:
UNIVESIDADE FEDEAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPATAMENTO DE MATEMÁTICA ª LISTA DE EXECÍCIOS DE CÁLCULO II-A Última atualizaçã 4-4-4 ) Determine e represente graficamente dmíni de cada uma das funções:
Thiago Lima de Menezes
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS DEPARTAMENTO DE ENGENHARIA ELÉTRICA Thiag Lima de Menezes Cnversr Push-Pull Alimentad em Crrente aplicad a Crreçã d Fatr de
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS DEPARTAMENTO DE ENGENHARIA ELÉTRICA Thiag Lima de Menezes Cnversr Push-Pull Alimentad em Crrente aplicad a Crreçã d Fatr de
Laboratório de Circuitos Elétricos II
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ ESCOLA POLITÉCNICA CURSO DE ENGENHARIA DE COMPUTAÇÃO DISCIPLINA DE CIRCUITOS ELÉTRICOS II NOME DO ALUNO: Laboratório de Circuitos Elétricos II Prof. Alessandro
PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ ESCOLA POLITÉCNICA CURSO DE ENGENHARIA DE COMPUTAÇÃO DISCIPLINA DE CIRCUITOS ELÉTRICOS II NOME DO ALUNO: Laboratório de Circuitos Elétricos II Prof. Alessandro
Transdutor de tensão alternada (analógico)
 [1] Intrduçã Os transdutres de tensã têm pr finalidade cnverter um determinad sinal de tensã em um sinal cntínu islad galvanicamente. Sã dispnibilizads s seguintes mdels: VA: para sistema cm frma de nda
[1] Intrduçã Os transdutres de tensã têm pr finalidade cnverter um determinad sinal de tensã em um sinal cntínu islad galvanicamente. Sã dispnibilizads s seguintes mdels: VA: para sistema cm frma de nda
TOE-50: Correção do fator de potência para cargas não lineares. Prof. Cassiano Rech
 TOE-50: Crreçã d fatr de ptência para cargas nã lineares Prf. Cassian Rech cassian@ieee.rg 1 Capítul 4 Crreçã ativa d fatr de ptência Principais métds utilizads Cnversr bst em md de cnduçã descntínua Cnversr
TOE-50: Crreçã d fatr de ptência para cargas nã lineares Prf. Cassian Rech cassian@ieee.rg 1 Capítul 4 Crreçã ativa d fatr de ptência Principais métds utilizads Cnversr bst em md de cnduçã descntínua Cnversr
Figura Diagrama unifilar de uma instalação eléctrica.
 9. Exempl 7 Cnsiderems a rede de distribuiçã representada na Figura 9.1. A canalizaçã QGBT-A é cnstituída pr um cab VAV 3x7+35 mm 2. A canalizaçã S1 alimenta um prédi nde existem 2 habitações cm ptência
9. Exempl 7 Cnsiderems a rede de distribuiçã representada na Figura 9.1. A canalizaçã QGBT-A é cnstituída pr um cab VAV 3x7+35 mm 2. A canalizaçã S1 alimenta um prédi nde existem 2 habitações cm ptência
Retificadores (ENG ) Lista de Exercícios (Selecionados) de Dispositivos Eletrônicos
 ista de Exercícis de ispsitivs Eletrônics etificadres (ENG - 20301) ista de Exercícis (Selecinads) de ispsitivs Eletrônics 06) etermine a queda de tensã direta através d did cujas características aparecem
ista de Exercícis de ispsitivs Eletrônics etificadres (ENG - 20301) ista de Exercícis (Selecinads) de ispsitivs Eletrônics 06) etermine a queda de tensã direta através d did cujas características aparecem
Transdutor de tensão alternada (analógico)
 Transdutr de tensã (analógic) Revisã 6.1 26/12/2012 [1] Intrduçã Os transdutres de tensã têm pr finalidade cnverter um determinad sinal de tensã em um sinal cntínu islad galvanicamente. Sã dispnibilizads
Transdutr de tensã (analógic) Revisã 6.1 26/12/2012 [1] Intrduçã Os transdutres de tensã têm pr finalidade cnverter um determinad sinal de tensã em um sinal cntínu islad galvanicamente. Sã dispnibilizads
8 FILTROS ATIVOS E DEFASADORES
 8 FILTOS ATIVOS E DEFASADOES Filtrs sã circuits elétrics que permitem passagem de crrente u tensã em uma faixa de freqüências inibem a passagem em utras freqüências. Filtrs ativs cm amp p s utilizam apenas
8 FILTOS ATIVOS E DEFASADOES Filtrs sã circuits elétrics que permitem passagem de crrente u tensã em uma faixa de freqüências inibem a passagem em utras freqüências. Filtrs ativs cm amp p s utilizam apenas
MATEMÁTICA APLICADA RESOLUÇÃO
 GRADUAÇÃO EM ADMINISTRAÇÃO, CIÊNCIAS ECONÔMICAS E 3/0/06 As grandezas P, T e V sã tais que P é diretamente prprcinal a T e inversamente prprcinal a V Se T aumentar 0% e V diminuir 0%, determine a variaçã
GRADUAÇÃO EM ADMINISTRAÇÃO, CIÊNCIAS ECONÔMICAS E 3/0/06 As grandezas P, T e V sã tais que P é diretamente prprcinal a T e inversamente prprcinal a V Se T aumentar 0% e V diminuir 0%, determine a variaçã
Vamos estudar as características e determinações do potencial da pilha e dos potenciais padrões do eletrodo e da pilha.
 Aula: 25 Temática: Ptenciais da Pilha Vams estudar as características e determinações d ptencial da pilha e ds ptenciais padrões d eletrd e da pilha. Uma pilha na qual a reaçã glbal ainda nã tenha atingid
Aula: 25 Temática: Ptenciais da Pilha Vams estudar as características e determinações d ptencial da pilha e ds ptenciais padrões d eletrd e da pilha. Uma pilha na qual a reaçã glbal ainda nã tenha atingid
4.1. Experiência Nº 4
 4.1 Experiência Nº 4 1. Assunt Circuits triásics equilibrads em regime permanente. 2. Objetivs Determinaçã de sequência de ases. Análise de circuits triásics equilibrads. Medidas de ptência. 3. Fundaments
4.1 Experiência Nº 4 1. Assunt Circuits triásics equilibrads em regime permanente. 2. Objetivs Determinaçã de sequência de ases. Análise de circuits triásics equilibrads. Medidas de ptência. 3. Fundaments
Centro Federal de Educação Tecnológica de Santa Catarina Departamento Acadêmico de Eletrônica Retificadores. Prof. Clóvis Antônio Petry.
 Centr Federal de Educaçã Tecnlógica de Santa Catarina Departament Acadêmic de Eletrônica Retificadres Circuits it em CA Série, Paralel e Mist Prf. Clóvis Antôni Petry. Flrianóplis, agst de 2008. Bibligrafia
Centr Federal de Educaçã Tecnlógica de Santa Catarina Departament Acadêmic de Eletrônica Retificadres Circuits it em CA Série, Paralel e Mist Prf. Clóvis Antôni Petry. Flrianóplis, agst de 2008. Bibligrafia
TÉCNICAS NÃO-PARAMÉTRICAS
 TÉCNICAS NÃO-PARAMÉTRICAS O pass inicial de qualquer análise estatística cnsiste em uma descriçã ds dads através de análise descritiva (tabelas, medidas e gráfics). Cm a presença de censura invalida esse
TÉCNICAS NÃO-PARAMÉTRICAS O pass inicial de qualquer análise estatística cnsiste em uma descriçã ds dads através de análise descritiva (tabelas, medidas e gráfics). Cm a presença de censura invalida esse
1ª Avaliação. 2) Qual dos gráficos seguintes representa uma função de
 1ª Avaliaçã 1) Seja f ( ) uma funçã cuj dmíni é cnjunt ds númers naturais e que asscia a td natural par valr zer e a td natural ímpar dbr d valr Determine valr de (a) f ( 3) e (b) + S, send f ( 4 ) * S
1ª Avaliaçã 1) Seja f ( ) uma funçã cuj dmíni é cnjunt ds númers naturais e que asscia a td natural par valr zer e a td natural ímpar dbr d valr Determine valr de (a) f ( 3) e (b) + S, send f ( 4 ) * S
e a susceptibilidade estão relacionadas por:
 49 3 Óptica Nã-linear A óptica nã-linear está assciada as fenômens óptics que surgem devid à interaçã nã-linear da luz cm a matéria. Estes fenômens smente sã bservads quand usams luz intensa n material.
49 3 Óptica Nã-linear A óptica nã-linear está assciada as fenômens óptics que surgem devid à interaçã nã-linear da luz cm a matéria. Estes fenômens smente sã bservads quand usams luz intensa n material.
QUARTA EXPERIÊNCIA DO LABORATÓRIO DE ONDAS TRANSFORMADORES DE QUARTO DE ONDA EWALDO ÉDER CARVALHO SANTANA JÚNIOR EE06115-67 TURMA2
 UNIVERSIDADE FEDERA DO MARANHÃO CENTRO DE CIÊNCIAS EXATAS E TECNOOGIA DEPARTAMENTE DE ENGENHARIA DA EETRICIDADE ABORATÓRIO DE ONDAS EETROMAGNÉTICAS QUARTA EXPERIÊNCIA DO ABORATÓRIO DE ONDAS TRANSFORMADORES
UNIVERSIDADE FEDERA DO MARANHÃO CENTRO DE CIÊNCIAS EXATAS E TECNOOGIA DEPARTAMENTE DE ENGENHARIA DA EETRICIDADE ABORATÓRIO DE ONDAS EETROMAGNÉTICAS QUARTA EXPERIÊNCIA DO ABORATÓRIO DE ONDAS TRANSFORMADORES
Caixas Ativas e Passivas. SKY 3000, SKY 2200, SKY 700, SKY 600 e NASH Áreas de Cobertura e Quantidade de Público
 Caixas Ativas e Passivas SKY 3000, SKY 00, SKY 700, SKY 600 e NASH 144 Áreas de Cbertura e Quantidade de Públic www.studir.cm.br Hmer Sette 18-07 - 01 A área cberta pelas caixas acima, em funçã d psicinament
Caixas Ativas e Passivas SKY 3000, SKY 00, SKY 700, SKY 600 e NASH 144 Áreas de Cbertura e Quantidade de Públic www.studir.cm.br Hmer Sette 18-07 - 01 A área cberta pelas caixas acima, em funçã d psicinament
Aula 8 Análise de circuitos no domínio da frequência e potência em corrente alternada
 ELETRICIDADE Aula 8 Análise de circuitos no domínio da frequência e potência em corrente alternada Prof. Marcio Kimpara Universidade Federal de Mato Grosso do Sul Associação de impedâncias As impedâncias
ELETRICIDADE Aula 8 Análise de circuitos no domínio da frequência e potência em corrente alternada Prof. Marcio Kimpara Universidade Federal de Mato Grosso do Sul Associação de impedâncias As impedâncias
IF-UFRJ FIW 362 Laboratório de Física Moderna Eletrônica Curso de Licenciatura em Física Prof. Antonio Carlos. Aula 6: Amplificadores Operacionais
 IFUFJ FIW 36 Labratóri de Física Mderna Eletrônica Curs de Licenciatura em Física Prf. Antni Carls Aula 6: Amplificadres Operacinais Este material fi basead em lirs e manuais existentes na literatura (ide
IFUFJ FIW 36 Labratóri de Física Mderna Eletrônica Curs de Licenciatura em Física Prf. Antni Carls Aula 6: Amplificadres Operacinais Este material fi basead em lirs e manuais existentes na literatura (ide
Informática II INFORMÁTICA II
 Jrge Alexandre jureir@di.estv.ipv.pt - gab. 30 Artur Susa ajas@di.estv.ipv.pt - gab. 27 1 INFORMÁTICA II Plan Parte I - Cmplementar cnheciment d Excel cm ferramenta de análise bases de dads tabelas dinâmicas
Jrge Alexandre jureir@di.estv.ipv.pt - gab. 30 Artur Susa ajas@di.estv.ipv.pt - gab. 27 1 INFORMÁTICA II Plan Parte I - Cmplementar cnheciment d Excel cm ferramenta de análise bases de dads tabelas dinâmicas
Eletrônica Básica - Curso Eletroeletrônica - COTUCA Lista 4 Análise de circuitos a diodos c.a.
 Eletrônica Básica - Curso Eletroeletrônica - COTUCA Lista 4 Análise de circuitos a diodos c.a. 1. A Figura abaixo apresenta o oscilograma da forma de onda de tensão em um determinado nó de um circuito
Eletrônica Básica - Curso Eletroeletrônica - COTUCA Lista 4 Análise de circuitos a diodos c.a. 1. A Figura abaixo apresenta o oscilograma da forma de onda de tensão em um determinado nó de um circuito
UFRJ/POLI/DEL - Laboratório de Eletrônica III. PARTE 1: Conversor de Impedância Negativa (NIC)
 Prática #3 CONVERSORES DE IMPEDÂNCIA GRUPO: Data: UFRJ/POLI/DEL Labratóri de Eletrônica III PARTE 1: Cnversr de Impedância Negativa (NIC) I) Objetiv Estudar a realizaçã e aplicaçã de cnversr de impedância
Prática #3 CONVERSORES DE IMPEDÂNCIA GRUPO: Data: UFRJ/POLI/DEL Labratóri de Eletrônica III PARTE 1: Cnversr de Impedância Negativa (NIC) I) Objetiv Estudar a realizaçã e aplicaçã de cnversr de impedância
Física FUVEST ETAPA. Resposta QUESTÃO 1 QUESTÃO 2. b) A energia cinética (E c ) do meteoro é dada por:
 Física QUSTÃO 1 Uma das hipóteses para explicar a extinçã ds dinssaurs, crrida há cerca de 6 milhões de ans, fi a clisã de um grande meter cm a Terra. stimativas indicam que meter tinha massa igual a 1
Física QUSTÃO 1 Uma das hipóteses para explicar a extinçã ds dinssaurs, crrida há cerca de 6 milhões de ans, fi a clisã de um grande meter cm a Terra. stimativas indicam que meter tinha massa igual a 1
Capítulo. Meta deste capítulo Entender o princípio de funcionamento de osciladores controlados por tensão.
 1 Osciladres Capítul Cntrlads pr Tensã Meta deste capítul Entender princípi de funcinament de sciladres cntrlads pr tensã. bjetivs Entender princípi de funcinament de sciladres cntrlads pr tensã; Analisar
1 Osciladres Capítul Cntrlads pr Tensã Meta deste capítul Entender princípi de funcinament de sciladres cntrlads pr tensã. bjetivs Entender princípi de funcinament de sciladres cntrlads pr tensã; Analisar
Trabalho Prático Nº 6.
 Trabalho Prático Nº 6. Título: Carga Predominantemente Resistiva, Carga Predominantemente Indutiva e Carga Resistiva e Indutiva em paralelo. Objetivo: Este trabalho prático teve como objetivo montar três
Trabalho Prático Nº 6. Título: Carga Predominantemente Resistiva, Carga Predominantemente Indutiva e Carga Resistiva e Indutiva em paralelo. Objetivo: Este trabalho prático teve como objetivo montar três
+ E - EEL211 - LABORATÓRIO DE CIRCUITOS ELÉTRICOS W= C.V J. v C(t)= i C(t).dt +V C(0) V. d i C(t)=C. v C(t) A dt. j 2 π f C
 11 - ABOATÓO D UTOS ÉTOS ABOATÓO N O 8: UTO APATVO () NDUTVO () M GM SNODA O bjetiv desta aula é verificar experimentalmente cmprtament d capacitr e indutr em regime de crrente alternada senidal. STA D
11 - ABOATÓO D UTOS ÉTOS ABOATÓO N O 8: UTO APATVO () NDUTVO () M GM SNODA O bjetiv desta aula é verificar experimentalmente cmprtament d capacitr e indutr em regime de crrente alternada senidal. STA D
Eletrônica de Potência II Capítulo 2
 Eletrônica de Ptência Capítul 2 Prf. uís M. Ndari luisndari@gmail.cm Prf. Cassian Rech 1 ntrduçã Em certas aplicações é necessári transfrmar uma tensã cntínua em utra cm amplitude regulada; Em sistemas
Eletrônica de Ptência Capítul 2 Prf. uís M. Ndari luisndari@gmail.cm Prf. Cassian Rech 1 ntrduçã Em certas aplicações é necessári transfrmar uma tensã cntínua em utra cm amplitude regulada; Em sistemas
