Integrais Resolução dos Exercícios Propostos
|
|
|
- Maria Braga César
- 7 Há anos
- Visualizações:
Transcrição
1 Intgrais Rsolução dos Ercícios Propostos Ercício : Encontr a intgral indfinida das sguints funçõs: t a) f( ) 7 + ; ) gt () + t t ; c) hu ( ) u( u+ u ); + d) f( ) ) + hv ( ) ( v ) f) gs ( ) s a) ( ) ( 7) ( 7 + ) d + + C ; ) c) d) ) f) t 6 + t dt t t + t + C t ; u + d ( ) d C + + ; ( + v ) dv ( v + v ) dv v + + C v v ds + C s s u ( u + u ) du ( u + u ) du u + C ; ; Ercício : Encontr a intgral indfinida das sguints funçõs: cos cos t + tg t sn cos a) f( ) ; ) gt () ; c) f( ) + 7sn cos t 7cos 7cos cos a) d cotg cossc d 7sn 7, mas pla tala d drivação dada no final do Fundamntum nº 7, otém-s qu: d cossc cossc cotg d cos Assim, d cossc + C 7sn 7 ) cos + tg cos snt dt t dt cost dt snt dt cos t + + cos t cos t t + tg t cotg tdt, mas novamnt pla tala d drivação dada no final do Fundamntum nº 7, otém-s qu: d sc sc tg, d cos t + tg t assim, dt sn t + sc t + C cos t
2 + ( tg ) sc d + d d sn cos c) 7cos 7cos 7 7 dada no final do fundamntum nº 7, otém-s qu: d tg sc, d sn cos assim, + d tg + C 7cos 7cos 7, mas novamnt pla tala d drivação Ercício : Calcul as sguints intgrais indfinidas, utilizando a técnica d sustituição: a) d ; ) d ; c) d ; d) sn + d ; ) cos( t t ) sc ( ) dt ; f) cos tdt; g) d ; h) d + 9 Sugstão para rsolvr o itm c: considr u + a) Fazmos u, logo du d, assim, d u du u C ( ) C ) Fazmos u, logo du d, assim, d ( u) du u + C ( ) + C c) Fazmos, conform sugstão u +, logo du d, assim, u u d du du + u u u u du u du u u + C ( + ) ( + ) + C d) Fazmos u, logo du d, assim, sn d sn u du cos u C cos C + + ) Fazmos u t, logo du 6t dt, assim, cos( t t ) dt cosu du snu + C snt + C + cost f) Fazmos cos t, assim, + cost cos tdt dt dt+ costdt t + sn t + C g) Fazmos u, logo du d, assim, sc ( ) d sc u du tg u + C tg( ) + C h) Fazmos u, logo du d, assim,
3 + 9 + u arctg arctg( ) d du u + C + C Ercício : Calcul as sguints intgrais, utilizando a técnica d intgração por parts a) d ; ) arcsn d + ; c) ( + )snd ; d) sn d ; ) cossc cotg d ; f) sn sc d a) Façamos u dv d, logo du d v +, assim, + d udv uv vdu + + d + + ( + ) + + C ( ) + + C ) Façamos u arcsn dv d, logo du d v, assim, arcsn d udv uv vdu arcsn d, fazndo agora t, tmos qu dt, assim, d du u ( ) Portanto, u arcsn d arcsn + + C c) Façamos u + dv sn d, logo du d v cos, assim, ( + )sn d ( + )cos + cos d (sn cos ) cos + C d) Sgu imdiatamnt do itm c qu snd sn cos + C Façamos ntão u dv sn d, logo du d v cos Portanto, Analisando a intgral sn d cos + cos d () cosd, osrvamos qu podmos calculá-la tamém por parts, fazndo agora u dv cos d, logo du d v sn, assim, cos d sn sn d pla osrvação acima, concluímos qu cos d sn (sn cos ) () Sustituindo () m (), otmos sn d cos + sn + 6 cos 6sn + C ) Façamos u cossc dv cossc cotg d, logo du cossc cotg d v cossc, assim, cossc cotg d cossc ( cossc )( cossc cotg ) d Logo, cossc cossc cotg d cossc Portanto, cossc cotg d + C f) Façamos u sn dv sc d, logo du cos d v tg, assim, sn sc d sn tg tg (cos d ) sn tg + sn d sn tg + cos + C
4 Ercício (rsolução com o uso d calculadora ou microcomputador): Escrva a soma d Rimann das sguints funçõs nos intrvalos indicados, usando a quantidad n d suintrvalos na partição considrada A sguir utiliz uma calculadora ou softwar para calcular o valor numérico da soma a) f( ), [,], n 7, n, n, n ; ) f ( ) sn, [, π ], n 6, n, n, n ; c) f ( ) cos, [, π ], n 6, n, n, n ; d) f ( ) cos sn, [, π ], n 6, n, n, n Ercício 6: Calcul, mdiant o Torma Fundamntal do Cálculo, as intgrais a sguir π π a) cos d; ) (cos sn ) d ; c) ( + ) d π d) sn d ; ) 9 π ( ) a) π π cos d sn snπ sn ) π π (cos sn ) d sn + cos snπ + cosπ sn cos c) ( + ) d + d) No itm d do rcício, vimos qu snd sn cos + C, assim, π π π sn d sn cos sn π π cosπ snπ + cosπ (+ π) π π ) Fazndo u, sgu qu: s, u, s, u du d, assim, 9 9 ( ) d u du u Ercício 7: Nos itns a sguir prss a ára das rgiõs limitadas plas curvas dadas Faça isso d duas maniras, com intgraçõs na variávl com intgraçõs na variávl Escolha uma das maniras calcul a ára a), + ) +, c) +,, a)
5 + P Para s ncontrar as coordnadas do ponto P dvmos tr +, ou sja Intgração na variávl : assim, AR ( ) d+ ( ) ua + d Intgração na variávl : AR ( ) [( ) d ] ( d ) ua ) P Q Para s ncontrar as coordnadas do ponto P dvmos tr, ou sja assim, Para s ncontrar as coordnadas do ponto Q dvmos tr, ou sja assim, Intgração na variávl : AR ( ) ( ) d+ ( ) ( ) d + ua
6 Intgração na variávl : AR ( ) ( d ) + ( d ) + ( ) c) P ua + S R O ponto P tm coordnada como +, tmos qu 6 O ponto Q tm coordnada como, tmos qu O ponto R tm coordnada como, tmos qu O ponto S tm coordnada como +, tmos qu Intgração na variávl : 6 AR ( ) ( + + ) d ( + ) d + + ua 6 Intgração na variávl : 6 AR ( ) ( + ) d+ ( + ) d+ ( ) d ( ) + ( ) ua 6 Ercício 8: Nos itns a sguir, apnas prss, mdiant intgrais dfinidas, a ára da rgião limitada plas curvas dadas Não é ncssário calcular a(s) intgral(is) a),, ),, a) Q
7 P S R Q O ponto P tm coordnada como, tmos qu O ponto Q tm coordnada como, tmos qu O ponto R tm coordnada como, tmos qu O ponto S tm coordnada como, tmos qu 8 Intgração na variávl : AR ( ) ( ) d Intgração na variávl : ) 8 8 AR ( ) ( ) d+ ( ) d+ ( ) d P S R Q
8 Para s ncontrar as coordnadas do ponto P dvmos tr, ou sja assim, + Para s ncontrar as coordnadas do ponto Q dvmos tr, ou sja assim, Para s ncontrar as coordnadas do ponto R dvmos tr, ou sja assim, O ponto S é a origm Assim, tmos Intgração na variávl : (7 ) (+ ) (7 ) (7 ) (+ ) (7 ) A( R ) ( ( )) d + ( ( )) d + ( ( )) d ( + ) d + ( + )) d + ( ) d Intgração na variávl : (+ ) + A( R ) ( ( + ) ) d + ( + + ) d + ( + ) d ( ) ( + ) + ( + 6) d+ ( + ) d+ ( + + ) d ( ) Ercício 9: Encontr o domínio as drivadas d primira d sgunda ordm das sguints funçõs: a) f ( ) ln( ) ; ) g ( ) ln ; c) h ( ) ln ; d) j ( ) sn(ln ) a) Dom f (,), 6 6( ) (6 ) f '( ) f "( ) ( ) ) g ( ) ln ln, assim, Dom g (, ) g'( ) g"( ) c) Dom h {, } ( ) ( + ) h'( ) h"( ) ( ) ( ) d) Dom j (, )
9 cos(ln ) j'( ) sn(ln ) cos(ln ) sn(ln ) cos(ln ) j "( ) + Ercício : Calcul as intgrais dadas a sguir + a) + d 6 ; ) ln d ; c) tg d; π d) cotg d; ) ln d π + ln a) + d d d C ln ln ln ) Fazndo u ln, tmos qu du d, assim, d c) Fazndo u cos, tmos qu du sn d, assim, sn du tg d d ln u C cos u + ln cos ln sc + C π d) Fazndo u sn, tmos qu: du cos d, além disso, s, ntão u ntão u Assim, cos du ln cotg d d ln u ln ln sn u π π π π ( ) ) Intgrando por parts, tommos u ln dv d, logo, du d v Assim, ln d ln d ln d ln + C ; s π, Ercício : Encontr a drivada das sguints funçõs: a) ln ; ) sn d) ( 7)( ) ; ) a) Como ln ln(sn ) ln ln(sn ), tmos: ( ) ln + ; c) ( 7) ( ) cos(ln ) ; cos ' ln + ln cotg + sn ) Como ( ) ln( + ) 9, tmos: ' ( ) ln( + ) + ( ) + 9 ( ) ( ) ln( + ) + + sn(ln ) c) Como cos(ln ), tmos: ' sn(ln ) d) ' ( )( ) + ( 7)
10 ) Tmos qu: ln ln ( 7) ( ) ln 7 + ln Drivando m ' rlação a, sgu qu: +, assim, 7 ' ( 7) ( ) + 7 Ercício : Calcul as drivadas das sguints funçõs a) f ( ) sn( ); ) g ( ) + ; c) h ( ) ln(cotg ); d) j ( ) sn( ) a) '( ) f cos( ) ) g'( ) + cos c) Como h ( ) ln( ) ln( cos ) ln( sn ), tmos: sn sn cos h'( ) (tg + cotg ) cos sn d) j'( ) sn( ) + cos( ) [sn( ) + cos( )] Ercício : Dadas as quaçõs a sguir, ncontr ' drivando-as implicitamnt m rlação a a) + + 7; ) sn a) + + ' + ( + '), logo, ' + ' ( + + ), assim, + + ', quando ( + ) ) sn + cos ' ( ' + ), logo, '( cos ) sn, assim, sn ', quando cos cos Ercício : Calcular as sguints intgrais: a) d ; ) ( + ) d ; c) sn( ) d ; ln( ) d) d ; ) d + u a) Fazndo a sustituição d variávl, otmos du d d u u d du + C + C
11 ( + ) d d + d + d ) u u + du + + C + + C u c) Fazndo a sustituição d variávis otmos du d d) + sn( ) d sn( )( d) snudu cosu+ C cos( ) + C d u + du ( ) d + d du ln u + C ln + + C u Ercício : A magnitud R d um trrmoto é mdida m uma scala, chamada scala Richtr, dada pla I fórmula R log, ond I é a intnsidad do trrmoto I é uma intnsidad padrão mínima S um I trrmoto ating a magnitud d 6, na scala Richtr, quantas vzs a intnsidad do trrmoto é maior qu a intnsidad padrão? Tmos R log I, assim, I I log 6, I I 6, I I I I I Portanto, a intnsidad do trrmoto é d 6, log 6, 89 vzs maior qu a intnsidad padrão Ercício 6: Uma contagm inicial numa cultura d actérias rvla a istência d 6 indivíduos Após horas o númro d indivíduos passa para 8 Sando-s qu a taa d crscimnto dssa spéci d actérias é proporcional ao númro d indivíduos prsnts, dtrmin uma prssão qu fornça o númro d indivíduos a cada instant t calcul o númro d actérias dpois d horas Tmos t horas 6 t horas 8 kt A taa d crscimnto é proporcional ao númro d indivíduos prsnts η () t M k η() M M M 6 k k η() 6 8 k ln ( ln) t ( ln) Então, η( t) 6 η() 6 7 Ercício 7: S acondicionarmos mg d um matrial radioativo numa caia d chumo sourmos qu a mia vida dss matrial é d anos, após quanto tmpo havrá mg do matrial dntro da caia? Tmos mg m t anos, média d vida anos mg m T anos Assim,
12 mg mg mg 6 mg t t / A li qu rg o dcaimnto radioativo é qt ( ) t T/ T/ T/ log log T ln log log T log (,989) 66, ln Portanto, havrá mg após aproimadamnt 66, anos Ercício 8: Com o auílio da Tala d Intgrais Imdiatas o uso das técnicas d intgração, calcul as sguints intgrais: a) tg udu; ) d ; c) + d ln ; d) cos sn d ; ) d ; g) + d ; f) ( + ) sn(ln ) tg(ln ) d ; h) d ; i) ln d ; j) arctg d ; k) d ; l) sn tg d d Fazndo a mudança d variávis d a) Tmos cos u sc du sn cos dv d v sc d tg cos otmos sn sn d sn tg (sn cos )tg d sn tg (sn cos ) d cos cos sn tg sn d sn tg [ cos ] d sn sn tg + Vrificação:
13 d sn (sn tg + ) sn costg + cos d sn sn + + cos cos tg + sn + cos tg u + ) Fazndo a sustituição d variávis otmos du d I du ln u + C ln + + C u u ln c) Fazndo a sustituição d variávis otmos du d + u u I d u du + C + C u + C ln + C ln + u sn d) Fazndo a sustituição d variávis otmos du cosd 6 sn 6 I u du u + C + C 6 6 u + ) Fazndo a sustituição d variávis du d otmos + u u I + d u du + C + C u + C u + C (+ ) + C + u + f) Fazndo a sustituição d variávis otmos du d I ( + ) d u du u + C ( + ) + C 8 u ln g) Fazndo a sustituição d variávis otmos du d sn(ln d ) I sn udu cosu+ C cos(ln ) + C
14 u ln h) Fazndo a sustituição d variávis otmos du d tg(ln ) I d tg udu ln sc u + C ln sc(ln ) + C du d u ln i) Fazndo a sustituição d variávis otmos dv v I ln d uv vdu ln d ln d ln + C (ln ) + C u arctg du d j) Fazndo a sustituição d variávis + otmos dv d v I arc tg d arc tg d arc tg dw + w arc tg ln w + C arc tg ln + + C u k) Fazndo a sustituição d variávis d otmos du u u I d du + C + C u l) Fazndo a sustituição d variávis otmos du 6 d I d du + C + C + C u u Ercício 9: Prov a fórmula da Tala d Intgrais, isto é, calcul sc d Sugstão: multipliqu divida sc por (sc + tg ) Tmos sc (sc + tg ) sc + sctg ) sc d d d sc + tg sc + tg Fazndo a sustituição d u sc + tg variávis otmos du (sctg + sc ) d (sc + sc tg ) d
15 sc + sc tg ) du d ln u + C ln sc + tg + C sc + tg u Ercício : Calcul as sguints intgrais indfinidas: a) d 6 ; ) + + d ; c) d (sinal trocado no dnominador); + + d) + + d ( )( ) ; ) d a) Tmos 6 ( )( + ) assim Logo, Portanto, A B A ( + ) + B ( ) ( )( + ) A( + ) + B( ) ( A+ B) + A B A+ B A A B B I d d ln + + C 6 + ) Tmos ( ) assim Logo, Portanto, c) Tmos + A B C A( ) + B( ) + C + + ( ) ( ) + ( A+ C) + B + A B A+ C A B B A B C + ln ln I d d + + d + + C + + ( + + ) Como < considramos Logo, + A B + C A( + + ) + ( B + C) ( A+ B) + ( A+ C) + A A+ B A A+ C B A C 8
16 Portanto, + 8 I d d + d d d 8 d Como d d arc tg( ) + C / u + + fazndo a mudança d variávis, lmrando qu du (6 + ) d , otmos 6 + d d d tg( ) 6 du arc + C u 6 /6 /6 ln u arctg( ) + C 6 /6 ln + + arctg( ) + C 6 /6 + + A B C D d) Tmos ( )( ) ( ) ( ) Logo, + + A( ) + B( )( ) + C( )( ) + D( ) ( A+ B) + ( 9A 7 B+ C) + (7A+ B C + D) + ( 7A 9B+ C D) A A+ B 9A 7B+ C B 7A+ B C + D 78 7A 9B C D C + D Portanto, I d d + + d + d ( )( ) ( ) ( ) 78 ln + ln + ( ) 9 ln + ln ( ) ( )
17 A B C D ) Tmos Logo, A( ) + B( ) + C ( ) + D ( + ) ( A+ B+ C) + ( B C + D) A B A+ B+ C A B C D + B A C B D Portanto, I d d + C Ercício : Rsolva as sguints intgrais indfinidas a) cos d; ) sn cos d ; c) cotg d; d) cossc d; ) tg sc d a) cos cos cos d ( + ) d ( cos ) + + d cos cos ( ) cos cos d + d + + d d + d + d d d + cosd + cosd + sn + sn + C ) sn cos d sn cos (cos d) sn ( sn )(cos d) sn sn )(cos d) Fazndo a mudança d variávis u sn du cosd otmos c) 6 6 sn sn )(cos d) ( u u ) du sn sn + C cotg d cotg cotg d cotg (cossc ) d cotg cossc d cotg d Fazndo a mudança d variávis u cotg du cossc d otmos cotg cossc d cotg d udu cotg d u ln sc + C cotg ln sc + C
18 d) cossc d cossc (cossc d ) u cossc du cossc cotg d dv cossc d v cotg vdu cossc cotg d cossc (cossc ) d cossc d cosscd Então, ` cossc d cossc cotg cossc d + cossc d cossc d cossc cotg + cossc d cossc d cossc cotg + cossc d cossccotg + ln cossc cotg + C ) I tg sc d tg (tg ) (sc ) sc sc + 7 I (sc sc + )sc d sc d sc d + sc d Para cada intgral acima usamos intgração por parts com dv sc d v tg u sc du sc sc tgd d dv sc v tg 7 sc d sc tg tg (sc sc tg d ) I sc d sc sc d u sc du sc tg d d dv sc v tg I sc tg tg sc d sc tg sc (sc ) d sc tg sc d + sc d sc d sctg scd sctg + ln sc + tg + C sc d (sc tg + ln sc + tg ) + C
19 I sc d sc sc d u sc du sc sc tgd d v tg dv sc I sc tg sc tg d sc tg sc (sc ) d sc tg sc d + sc d sc d sc tg + (sc tg + ln sc + tg ) sc d sc tg + (sc tg + ln sc + tg ) + C 8 7 I sc d sc sc d u sc du sc sc tgd d v tg dv sc I sc tg sc tg d sc tg sc (sc ) d 7 sc tg sc d + sc d 7 6sc d sc tg + sc tg + (sctg + ln sc + tg ) 8 7 I sc d sc tg + sc tg + (sctg + ln sc + tg ) + C 6 8 Ercício : Calcul as sguints intgrais: a) d d + ; c) d) d (corrigido colocando raiz no dnominador);) d ; 6 a) Fazndo a sustituição d variávis a, snθ snθ d cos θdθ, cosθ cos θ, otmos d ;f) d 9 9 ( ) /
20 cosθ I d d cossc d θ θ θ snθcosθ / ln cosscθ cotg θ + C ln + C / / ln + C ) Fazndo a sustituição d variávis a, tgθ snθ otmos c) Fazndo a sustituição d variávis d sc θdθ, + scθ cosθ d sc θ cosθ I dθ dθ tgθ scθ + cosθ snθ cosscθdθ ln cosscθ cotg θ + C ln + C ln + C Otmos 6sc θ, d 6scθtgθdθ 6 6tg θ, snθ 6 scθ tgθ I d cos dθ θdθ 6 6sc θ 6tg θ 6 snθ + C + C d) Fazndo a sustituição d variávis sc θ, d scθtgθdθ otmos tg θ, snθ 6 scθ I d scθtgθdθ sc θdθ tgθ C + tgθ + C + C
21 ) Tmos I d d d ( ) (7/) 9 Fazndo a sustituição d variávis 7 7 sc θ, d scθtgθdθ Otmos / tg θ, sn θ, cosθ scθtgθ I sc ln sc tg ln d θ θ d θ θ θ C C tgθ / d d d f) Tmos I ( ) ( ) ( ) 8 ( ) Fazndo a sustituição d variávis otmos sc θ, d scθtg θdθ, tgθ θ θ scθ tgθ θ θ θ I d sc d cos d 8 tg θ 8 tg θ 8 sn θ cosθ u snθ Fazndo a sustituição d variávis otmos du cosθdθ I ( ) 8 du + C + C + C + C u 8 u 8snθ 8 8 Ercício : Mostr qu o volum do con circular rto d altura h raio da as r é dado por π r h Sugstão: Rotacion um triângulo rtângulo adquado, cujos cattos stão sor os ios coordnados h h m r h h r h + h r r
22 r r h h h V π[ + h] d (π πh) d π πh r + + r r hr r r r hr + hr hr π + πh π( h) + πh π π πr h r 6 6 r Ercício : Encontr a ára d um tronco d con circular rto d altura h raios r r h r r h m r r h ( r ) r r h f ( ) ( r ) r r πhr é o volum do cilindro intrno r r r h h hr π π π r r r r r r r r r V V f( ) d [ ( r )] d ( + ) d O volum é r h hr h r hr r h r hr r π + π + π + r r r r r r r r r r r r r hr + hrr hr π 6( r r ) π hr + hrr hr r r πhr π hr + hrr hr ( r r) πhr + π( hr + hrr hr ) + r r ( r r) π hr r hr + hr + hr r hr ) π h r r r r r r r r r r r [ + + ] π h [6r r r + r ] r r Ercício : Considr a rgião R, limitada plas curvas:, + a rgião R, limitada plas curvas: +, Considr os sólidos S S otidos, rspctivamnt, pla rvolução das rgiõs R R ao rdor do io O Considr os sólidos S S
23 otidos, rspctivamnt, pla rvolução das rgiõs R R ao rdor do io O Eprss, mas não calcul, o volum dos sólidos S, S, S S mdiant o uso d intgrais Faça isso d duas maniras, com intgraçõs na variávl na variávl ou / ou / r (/,/) R / ou r R - ou - / + ou -+ Intgração m π + π + π + π π + π VS ( ) π d+ π( + ) d VS ( ) d ( ) ( ) d V( S ) [( ) ( ) ] d [( ) ( ) ] d VS ( ) ( d ) ( d ) Intgração m VS ( ) π [( + ) ( )] d π + π + π π + π VS ( ) [( ) ( ) ] d VS ( ) [( ) ( )] d [( ) ( )] d VS ( ) [( ) ( ) ] d [( ) ( ) ] d
24 Ercício 6: Considr a rgião R, limitada plas curvas: +,, Considr o sólido S otido pla rvolução d R ao rdor do io O Eprss, mas não calcul, o volum d S mdiant o uso d intgrais Faça isso d duas maniras, com intgraçõs na variávl na variávl 6 + ou - ou + Intgração m : Intgração m : π [( + ) ( )] d - 6 π[( ) ] d + π[( + ) ( ) ] d+ π[() ( ) ] d Ercício 7: Calcul o volum do sólido S, situado ntr os planos prpndiculars ao io O m m, com a as no plano, limitada pla paráola, sando qu suas sçõs transvrsais são quadrados A as do sólido S é a rgião do plano limitada pla paráola a rta
25 Para cada [,] o lado do quadrado tm mdida igual a Logo, a ára do quadrado é igual a ( >!) Então V A( ) d d O volum do sólido é unidads d volum Ercício 8: Mostr, mdiant o uso da técnica do volum por fatiamnto, qu o volum da pirâmid d altura h as quadrada d lado l é dado por V l h S considrarmos o io vrtical como prolongamnto da altura da pirâmid orintado para cima podmos dscorir a ára A ( ) do quadrado otido como fatiamnto da pirâmid pla família d planos parallos à as da msma mdiant smlhança d triângulos h h h ( h ) h ( ) h h l/ Na altura, o lado do quadrado é igual a h ( ) Então h ( h ) A ( ) h h h h ( h ) V A( ) d d ( h ) d h h h h V h h ( h ) ( h h) ( h ) h ( h ) d (ára da as)(altura) h Ercício 9: Encontr o comprimnto do arco sor a curva + do ponto (, ) ao ponto (, ) Tmos d d + O comprimnto do arco dsjado é dado por ( 9 ) s + d + d
26 u + 9 du d Fazndo a mudança d variávl 9 u u otmos udu 9 ( ) 7 7 s ( ) (,6 ) 9,7unidads Ercício : Encontr o comprimnto do arco sor o gráfico da função ascissa ao ponto d ascissa f( ) + do ponto d 6 Tmos f ( ) + f ( ) ( 6 ) Assim o comprimnto do arco dsjado é dado por ( ) ( ) d d d d 8 ( ) d d d d d d 8 unidads s + d + + d + + d Ercício : Calcul a ára da suprfíci otida ao rotacionarmos o arco do gráfico d f ( ) ntr os pontos (,) (,) ao rdor do io O A curva é part d uma paráola, ao sr rotacionada ao rdor do io O, gra o paraolóid, conform a figura a sguir d d A π + ( ) d π + d π + d
27 u + du d Fazndo a mudança d variávl u u 7 tmos 7 7 π ( ) ( ) π ( ) ( ) π π A π udu π u ( ) ( ) ,8 unidads quadradas Ercício : Considr o arco do gráfico d f ( ) ntr os pontos (,) (,8) Calcul a ára da suprfíci otida ao girarmos ss arco ao rdor do io O A curva a suprfíci d rvolução stão rprsntados a sguir A π + ( ) d π + 9 d u + 9 du 6 Fazndo a mudança d variávl tmos u u π 7 u π π π A π du u ( ) ( ) (,,6) 99, unidads quadradas Ercício : Esoc a rgião idntificada com a intgral imprópria do Emplo 8
28 A intgral do mplo 8 é d lim d - O Ercício : Encontr os valors d k para os quais a intgral imprópria o valor da intgral k k k k k d d k k k lim lim lim ( ) k d convrg dtrmin k S k >, lim ( ) Logo k k d é divrgnt para k > k k d k k é divrgnt para k k lim Logo d k S k <, lim ( ) Logo S k, d d lim ] Portanto a intgral imprópria k > d é convrgnt para todo k < é divrgnt para k Ercício : Considr a rgião ilimitada R, acima do io O aaio do gráfico da função f( ) situado sor o intrvalo [, ) Mostr qu o volum do sólido ilimitado otido pla rotação d R m torno do io O é igual a π unidads cúicas
29 / O d Osrv qu: spssura do disco: d ; raio do disco: ; volum do disco: π( ) d Assim, V π d lim π d lim π π lim ( ) π Ercício 6: Dtrmin s a intgral imprópria é convrgnt ou divrgnt, no caso d sr convrgnt, calcul o valor da intgral (a) sn d; () d ; (c) d ; (d) ln d; () d ; (f) d ; ln (g) ln d; (h) ln d ( ) Como assum a) sn d lim sn d lim cos] lim (cos cos) lim ( cos ) todos os valors d nπ nπ, ntão cos assum todos os valors d a Portanto, lim cos não ist Consquntmnt a intgral imprópria divrg
30 ) d lim d Inicialmnt vamos rsolvr a intgral a a u du d d variávl a u a u Portanto, otmos a d Fazndo a mudança u a a u a d du ( ( ) ( ) ( ) a ln a ln ln ln ln a a a ln ln d lim [ ( )] c) Fazndo a mudança d variávl d lim d u du d dv v otmos d d + d Portanto, Assim, d ( ) ( ) + d lim ( + ) lim lim + Osrv qu lim é uma indtrminação do tipo, nst caso, podmos aplicar a rgra d L Hospital, isto é, lim lim Logo, d) lim lim d + + ln d lim ln d Rsolvndo a intgral por parts tmos u ln du d dv d v Logo, Assim, ln d ln d ln d ln ] ln d ln ln ( ) ln + ln d lim ( ln + ) Portanto a intgral divrg
31 d lim a ( + )( ) a ) d A + B ( ) + ( + ) ( + ) + + ( + )( ) A B A B A B A+ B A A B + B d ( ) ( ) lim ( ) lim ( ) a + + d + + d + d + + d ( ) ( ) a lim ( ln + + ln + + lim ( ln + + ln + a + ( ) lim ( ln + + ln + ln a ( a a ) + lim ( ln + ln + ln Osrv qu os limits acima não istm, pois lim ln lim ln a Portanto a intgral imprópria divrg Not qu, nst caso, astaria analisar apnas uma das intgrais da parcla inicial + a + a d d lim (ln ) (ln ) Fazndo a mudança d variávl f) u ln du d otmos ln d du u (ln ) ln u ln + d Portanto, lim ( + ) A intgral imprópria convrg para (ln ) ln g) ln d lim ln d + Mas, plo ítm d) tm-s qu ln d (ln ) Logo, ε ε ] ln d (ln ) (ln ) ε(lnε ) εlnε + ε ε lnε ln d lim ( ε ln ε + ε) lim + lim ε + + ε + ε ε ε Aplicando a rgra d L Hospital, vm lnε lim ε lim lim ε + ε + ε ε + ε ε Portanto a intgral imprópria convrg para zro
32 h) ln d ln d+ ln d lim ln d+ lim ln d Vamos calcular inicialmnt a intgral lim ln d + a a + a a lim ln d lim ln lim [ a(lna )] lim alna+ lim lna ] a a a a a a a Pla rsolução do itm g), tm-s qu Vamos calcular agora lim Portanto, a intgral imprópria ln d lim alna Logo a + lim ln d + a a lim ln d lim (ln ) ] lim (ln ) ln d divrg
1. (2,0) Um cilindro circular reto é inscrito em uma esfera de raio r. Encontre a maior área de superfície possível para esse cilindro.
 Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
01.Resolva as seguintes integrais:
 INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA MAT A CÁLCULO A a LISTA DE EXERCÍCIOS Atualizada m 7..Rsolva as sguints intgrais: 5.).).).) sn().5) sn cos.) tg 5 sc.7).8).9) ln 5.) arctg.).).).).7)
INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA MAT A CÁLCULO A a LISTA DE EXERCÍCIOS Atualizada m 7..Rsolva as sguints intgrais: 5.).).).) sn().5) sn cos.) tg 5 sc.7).8).9) ln 5.) arctg.).).).).7)
Derivada Escola Naval
 Drivada Escola Naval EN A drivada f () da função f () = l og é: l n (B) 0 l n (E) / l n EN S tm-s qu: f () = s s 0 s < < 0 s < I - f () só não é drivávl para =, = 0 = II - f () só não é contínua para =
Drivada Escola Naval EN A drivada f () da função f () = l og é: l n (B) 0 l n (E) / l n EN S tm-s qu: f () = s s 0 s < < 0 s < I - f () só não é drivávl para =, = 0 = II - f () só não é contínua para =
1 - RECORDANDO 2 - INTERSEÇÃO ENTRE RETA E CIRCUNFERÊNCIA. Exercício Resolvido 1: Frente III. na última equação, tem-se:
 Matmática Frnt III CAPÍTULO 23 POSIÇÕES RELATIVAS ENTRE RETA E CIRCUNFERÊNCIA 1 - RECORDANDO Na aula passada, nós vimos as quaçõs da circunfrência, tanto com cntro na origm ( ) como a sua quação gral (
Matmática Frnt III CAPÍTULO 23 POSIÇÕES RELATIVAS ENTRE RETA E CIRCUNFERÊNCIA 1 - RECORDANDO Na aula passada, nós vimos as quaçõs da circunfrência, tanto com cntro na origm ( ) como a sua quação gral (
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA MAT 195 CÁLCULO DIFERENCIAL E INTEGRAL I Atualizada em A LISTA DE EXERCÍCIOS
 INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA MAT 9 CÁLCULO DIFERENCIAL E INTEGRAL I Atualizada m 00. A LISTA DE EXERCÍCIOS Drivadas d Funçõs Compostas 0. Para cada uma das funçõs sguints,
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA MAT 9 CÁLCULO DIFERENCIAL E INTEGRAL I Atualizada m 00. A LISTA DE EXERCÍCIOS Drivadas d Funçõs Compostas 0. Para cada uma das funçõs sguints,
5.10 EXERCÍCIO pg. 215
 EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção
EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA LIMITES E DERIVADAS MAT B Prof a Graça Luzia
 INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA LIMITES E DERIVADAS MAT B - 008. Prof a Graça Luzia A LISTA DE EXERCÍCIOS ) Usando a dfinição, vrifiqu s as funçõs a sguir são drivávis m 0 m
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA LIMITES E DERIVADAS MAT B - 008. Prof a Graça Luzia A LISTA DE EXERCÍCIOS ) Usando a dfinição, vrifiqu s as funçõs a sguir são drivávis m 0 m
2 x. ydydx. dydx 1)INTEGRAIS DUPLAS: RESUMO. , sendo R a região que. Exemplo 5. Calcule integral dupla. xda, no retângulo
 Intgração Múltipla Prof. M.Sc. Armando Paulo da Silva UTFP Campus Cornélio Procópio )INTEGAIS DUPLAS: ESUMO Emplo Emplo Calcul 6 Calcul 6 dd dd O fato das intgrais rsolvidas nos mplos srm iguais Não é
Intgração Múltipla Prof. M.Sc. Armando Paulo da Silva UTFP Campus Cornélio Procópio )INTEGAIS DUPLAS: ESUMO Emplo Emplo Calcul 6 Calcul 6 dd dd O fato das intgrais rsolvidas nos mplos srm iguais Não é
ESCOLA SECUNDÁRIA DE ALCÁCER DO SAL. 11º Ano. MATEMÁTICA Exercícios de Exames e Testes Intermédios. Ano Letivo de 2012/2013
 ESCOLA SECUNDÁRIA DE ALCÁCER DO SAL MATEMÁTICA Exrcícios d Exams Tsts Intrmédios 11º Ano Ano Ltivo d 2012/2013 Trigonomtria 1 Na figura stá rprsntado o quadrado é a amplitud m radianos do ângulo Mostr
ESCOLA SECUNDÁRIA DE ALCÁCER DO SAL MATEMÁTICA Exrcícios d Exams Tsts Intrmédios 11º Ano Ano Ltivo d 2012/2013 Trigonomtria 1 Na figura stá rprsntado o quadrado é a amplitud m radianos do ângulo Mostr
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 21 DE JULHO Grupo I. Questões
 PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 63) ª FASE 1 DE JULHO 014 Grupo I Qustõs 1 3 4 6 7 8 Vrsão 1 C B B D C A B C Vrsão B C C A B A D D 1 Grupo II 11 O complo
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 63) ª FASE 1 DE JULHO 014 Grupo I Qustõs 1 3 4 6 7 8 Vrsão 1 C B B D C A B C Vrsão B C C A B A D D 1 Grupo II 11 O complo
UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO
 UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO 0 Nos rcícios a) ), ncontr a drivada da função dada, usando a dfinição a) f ( ) + b) f ( ) c) f ( ) 5 d) f ( )
UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO 0 Nos rcícios a) ), ncontr a drivada da função dada, usando a dfinição a) f ( ) + b) f ( ) c) f ( ) 5 d) f ( )
Função do 2 o Grau. Uma aplicação f der emr
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA. Dfinição Uma aplicação f
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA. Dfinição Uma aplicação f
tg 2 x , x > 0 Para determinar a continuidade de f em x = 0, devemos calcular os limites laterais
 UFRGS Instituto d Matmática DMPA - Dpto. d Matmática Pura Aplicada MAT 0 353 Cálculo Gomtria Analítica I A Gabarito da a PROVA fila A 5 d novmbro d 005 Qustão (,5 pontos Vrifiqu s a função f dada abaixo
UFRGS Instituto d Matmática DMPA - Dpto. d Matmática Pura Aplicada MAT 0 353 Cálculo Gomtria Analítica I A Gabarito da a PROVA fila A 5 d novmbro d 005 Qustão (,5 pontos Vrifiqu s a função f dada abaixo
Resolução do exame de Análise Matemática I (24/1/2003) Cursos: CA, GE, GEI, IG. 1ª Chamada
 Rsolução do am d nális Matmática I (//) Cursos: C, GE, GEI, IG ª Chamada Ercício > > como uma função ponncial d bas mnor do qu ntão o gráfico dsta função é o rprsntado na figura ao lado. Esta função é
Rsolução do am d nális Matmática I (//) Cursos: C, GE, GEI, IG ª Chamada Ercício > > como uma função ponncial d bas mnor do qu ntão o gráfico dsta função é o rprsntado na figura ao lado. Esta função é
UFJF ICE Departamento de Matemática Cálculo I Terceira Avaliação 10/07/2010 FILA A Aluno (a): Matrícula: Turma:
 UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação 0/07/00 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha.
UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação 0/07/00 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha.
Memorize as integrais imediatas e veja como usar a técnica de substituição.
 Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática
 Univrsidad Fdral do Rio d Janiro Instituto d Matmática Dpartamnto d Matmática Gabarito da Prova Final d Cálculo Difrncial Intgral II - 07-I (MAC 8 - IQN+IFN+Mto, 6/06/07 Qustão : (.5 pontos Rsolva { xy.
Univrsidad Fdral do Rio d Janiro Instituto d Matmática Dpartamnto d Matmática Gabarito da Prova Final d Cálculo Difrncial Intgral II - 07-I (MAC 8 - IQN+IFN+Mto, 6/06/07 Qustão : (.5 pontos Rsolva { xy.
Lista 5: Regras de Derivação
 Univrsidad Fdral do Val do São Francisco Câmpus Juaziro BA Colgiado d Engnharia Elétrica Prof. Pdro Macário d Moura Cálculo Difrncial Intgral Lista : Rgras d Drivação 0. Calcular as drivadas das prssõs
Univrsidad Fdral do Val do São Francisco Câmpus Juaziro BA Colgiado d Engnharia Elétrica Prof. Pdro Macário d Moura Cálculo Difrncial Intgral Lista : Rgras d Drivação 0. Calcular as drivadas das prssõs
1.1 O Círculo Trigonométrico
 Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
Definição de Área entre duas curvas - A área A entre região limitada pelas curvas. x onde f e g são contínuas e x g x
 Aula Capítulo 6 Aplicaçõs d Intração (pá. 8) UFPA, d junho d 5 Ára ntr duas curvas Dinição d Ára ntr duas curvas - A ára A ntr rião limitada plas curvas a y plas rtas a,, é ond são contínuas A a d y para
Aula Capítulo 6 Aplicaçõs d Intração (pá. 8) UFPA, d junho d 5 Ára ntr duas curvas Dinição d Ára ntr duas curvas - A ára A ntr rião limitada plas curvas a y plas rtas a,, é ond são contínuas A a d y para
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 21 DE JULHO 2014 Grupo I.
 Associação d Profssors d Matmática Contactos: Rua Dr João Couto, nº 7-A 100-6 Lisboa Tl: +1 1 716 6 90 / 1 711 0 77 Fa: +1 1 716 64 4 http://wwwapmpt mail: gral@apmpt PROPOSTA DE RESOLUÇÃO DA PROVA DE
Associação d Profssors d Matmática Contactos: Rua Dr João Couto, nº 7-A 100-6 Lisboa Tl: +1 1 716 6 90 / 1 711 0 77 Fa: +1 1 716 64 4 http://wwwapmpt mail: gral@apmpt PROPOSTA DE RESOLUÇÃO DA PROVA DE
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
ˆ y. Calcule x e y. B P C 14. Na figura, o quadrilátero ABCD está circunscrito na circunferência de centro O. Sendo
 LIST 02 XRÍIOS GOTRI PLN PROF. ROGRINHO 1º nsino édio (Tangência ângulos na circunf. quadrilátros pontos notávis do torma d Tals smlhança d a) Nom: n turma 08. No rtângulo da figura ao lado tm-s qu: ˆ
LIST 02 XRÍIOS GOTRI PLN PROF. ROGRINHO 1º nsino édio (Tangência ângulos na circunf. quadrilátros pontos notávis do torma d Tals smlhança d a) Nom: n turma 08. No rtângulo da figura ao lado tm-s qu: ˆ
Adriano Pedreira Cattai
 Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
III Integrais Múltiplos
 INTITUTO POLITÉCNICO DE TOMA Escola uprior d Tcnologia d Tomar Ára Intrdpartamntal d Matmática Anális Matmática II III Intgrais Múltiplos. Calcul o valor dos sguints intgrais: a) d d ; (ol. /) b) d d ;
INTITUTO POLITÉCNICO DE TOMA Escola uprior d Tcnologia d Tomar Ára Intrdpartamntal d Matmática Anális Matmática II III Intgrais Múltiplos. Calcul o valor dos sguints intgrais: a) d d ; (ol. /) b) d d ;
A seção de choque diferencial de Rutherford
 A sção d choqu difrncial d Ruthrford Qual é o ângulo d dflxão quando a partícula passa por um cntro d força rpulsiva? Nss caso, quando tratamos as trajtórias sob a ação d forças cntrais proporcionais ao
A sção d choqu difrncial d Ruthrford Qual é o ângulo d dflxão quando a partícula passa por um cntro d força rpulsiva? Nss caso, quando tratamos as trajtórias sob a ação d forças cntrais proporcionais ao
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Material Teórico - Círculo Trigonométrico. Secante, cossecante e cotangente. Primeiro Ano do Ensino Médio
 Matrial Tórico - Círculo Trigonométrico Scant, cosscant cotangnt Primiro Ano do Ensino Médio Autor: Prof. Fabrício Siquira Bnvids Rvisor: Prof. Antonio Caminha M. Nto 5 d dzmbro d 08 Invrsas numéricas:
Matrial Tórico - Círculo Trigonométrico Scant, cosscant cotangnt Primiro Ano do Ensino Médio Autor: Prof. Fabrício Siquira Bnvids Rvisor: Prof. Antonio Caminha M. Nto 5 d dzmbro d 08 Invrsas numéricas:
Exame de Matemática Página 1 de 6. obtém-se: 2 C.
 Eam d Matmática -7 Página d 6. Simplificando a prssão 9 ( ) 6 obtém-s: 6.. O raio r = m d uma circunfrência foi aumntado m 5%. Qual foi o aumnto prcntual da ára da sgunda circunfrência m comparação com
Eam d Matmática -7 Página d 6. Simplificando a prssão 9 ( ) 6 obtém-s: 6.. O raio r = m d uma circunfrência foi aumntado m 5%. Qual foi o aumnto prcntual da ára da sgunda circunfrência m comparação com
Matemática IME-2007/ a QUESTÃO. 2 a QUESTÃO COMENTA
 Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
UFJF ICE Departamento de Matemática Cálculo I Terceira Avaliação 03/12/2011 FILA A Aluno (a): Matrícula: Turma: x é: 4
 UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação 0/1/011 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: 1- A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação 0/1/011 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: 1- A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
Hewlett-Packard MATRIZES. Aulas 01 a 06. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MATRIZES Aulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MATRIZES NOÇÃO DE MATRIZ REPRESENTAÇÃO DE UMA MATRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDAMENTAL MATRIZES ESPECIAIS IGUALDADE
Hwltt-Packard MATRIZES Aulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MATRIZES NOÇÃO DE MATRIZ REPRESENTAÇÃO DE UMA MATRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDAMENTAL MATRIZES ESPECIAIS IGUALDADE
( ) π π. Corolário (derivada da função inversa): Seja f uma função diferenciável e injectiva definida num intervalo I IR.
 Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA
 Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
1) Determine o domínio das funções abaixo e represente-o graficamente: 1 1
 ) Dtrmin dmíni das funçõs abai rprsnt- graficamnt: z + z 4.ln( ) z ln z z arccs( ) f) z g) z ln + h) z ( ) ) Dtrmin dmíni, trac as curvas d nívl sbc gráfic das funçõs: f (, ) 9 + 4 f (, ) 6 f (, ) 6 f
) Dtrmin dmíni das funçõs abai rprsnt- graficamnt: z + z 4.ln( ) z ln z z arccs( ) f) z g) z ln + h) z ( ) ) Dtrmin dmíni, trac as curvas d nívl sbc gráfic das funçõs: f (, ) 9 + 4 f (, ) 6 f (, ) 6 f
Quadro de Respostas das Questões de Múltipla Escolha Valor: 65 pontos Alternativa/Questão Rascunho A B C D E. 1 e.
 UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação /08/0 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação /08/0 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
Hewlett-Packard MATRIZES. Aulas 01 a 05. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MTRIZES ulas 0 a 05 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE ENTRE
Hwltt-Packard MTRIZES ulas 0 a 05 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE ENTRE
Arcos e ângulos Adote π=3,14 quando necessário.
 Prof. Liana Turmas: 1C17/27/37 Sgundo trimstr Ângulos Complmntars Suplmntars 1. Qual é o ângulo qu xcd o su suplmnto m 66? 2. Dtrmin um ângulo sabndo qu o su suplmnto xcd o próprio ângulo m 70. 3. Qual
Prof. Liana Turmas: 1C17/27/37 Sgundo trimstr Ângulos Complmntars Suplmntars 1. Qual é o ângulo qu xcd o su suplmnto m 66? 2. Dtrmin um ângulo sabndo qu o su suplmnto xcd o próprio ângulo m 70. 3. Qual
( ) a. 2 e x dx = 2. b. 2 = e dx. e dx e 2 dx. = u. Integrais Exponenciais e Logarítmicas. e dx = e du = e + C dx
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. Aplicação da rgra
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. Aplicação da rgra
Guias de ondas de seção transversal constante
 Guias d ondas d sção transvrsal constant Ants d considrarmos uma aplicação spcífica, suponhamos um tubo rto, oco infinito, fito d matrial condutor idal, com sção transvrsal constant. Vamos considrar qu
Guias d ondas d sção transvrsal constant Ants d considrarmos uma aplicação spcífica, suponhamos um tubo rto, oco infinito, fito d matrial condutor idal, com sção transvrsal constant. Vamos considrar qu
Hewlett-Packard MATRIZES. Aulas 01 a 06. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MTRIZES ulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz no 06 Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE
Hwltt-Packard MTRIZES ulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz no 06 Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE
Sala: Rúbrica do Docente: Registo:
 Instituto Suprior Técnico Dpartamnto d Matmática Scção d Àlgbra Anális o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I (MEFT, LMAC, MEBiom) o Sm. 0/ 4/Jan/0 Duração: h30mn Instruçõs Prncha os sus dados na
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Àlgbra Anális o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I (MEFT, LMAC, MEBiom) o Sm. 0/ 4/Jan/0 Duração: h30mn Instruçõs Prncha os sus dados na
, ou seja, 8, e 0 são os valores de x tais que x e, Página 120
 Prparar o Eam 0 07 Matmática A Página 0. Como g é uma função contínua stritamnt crscnt no su domínio. Logo, o su contradomínio é g, g, ou sja, 8,, porqu: 8 g 8 g 8 8. D : 0, f Rsposta: C Cálculo Auiliar:
Prparar o Eam 0 07 Matmática A Página 0. Como g é uma função contínua stritamnt crscnt no su domínio. Logo, o su contradomínio é g, g, ou sja, 8,, porqu: 8 g 8 g 8 8. D : 0, f Rsposta: C Cálculo Auiliar:
TÓPICOS. EDO de variáveis separadas. EDO de variáveis separáveis. EDO homogénea. 2. Equações Diferenciais de 1ª Ordem.
 ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
Cálculo Diferencial e Integral II
 Cálculo Difrncial Intgral II Lista 7 - Rsumo a Toria A Rgra a Caia No stuo funçõs uma variávl usamos a Rgra a Caia para calcular a rivaa uma função composta Nst caso sno w f uma função ifrnciávl sno g
Cálculo Difrncial Intgral II Lista 7 - Rsumo a Toria A Rgra a Caia No stuo funçõs uma variávl usamos a Rgra a Caia para calcular a rivaa uma função composta Nst caso sno w f uma função ifrnciávl sno g
log 2, qual o valor aproximado de 0, 70
 UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
PSI-2432: Projeto e Implementação de Filtros Digitais Projeto Proposto: Conversor de taxas de amostragem
 PSI-2432: Projto Implmntação d Filtros Digitais Projto Proposto: Convrsor d taxas d amostragm Migul Arjona Ramírz 3 d novmbro d 2005 Est projto consist m implmntar no MATLAB um sistma para troca d taxa
PSI-2432: Projto Implmntação d Filtros Digitais Projto Proposto: Convrsor d taxas d amostragm Migul Arjona Ramírz 3 d novmbro d 2005 Est projto consist m implmntar no MATLAB um sistma para troca d taxa
Função Exponencial: Conforme já vimos, o candidato natural à função exponencial complexa é dado pela função. f z x iy f z e cos y ie sen y.
 Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Prova Escrita de Matemática A 12. o Ano de Escolaridade Prova 635/Versões 1 e 2
 Eam Nacional d 0 (. a fas) Prova Escrita d Matmática. o no d Escolaridad Prova 3/Vrsõs GRUPO I Itns Vrsão Vrsão. (C) (). () (C) 3. () (C). (D) (). (C) (). () () 7. () (D) 8. (C) (D) Justificaçõs:. P( )
Eam Nacional d 0 (. a fas) Prova Escrita d Matmática. o no d Escolaridad Prova 3/Vrsõs GRUPO I Itns Vrsão Vrsão. (C) (). () (C) 3. () (C). (D) (). (C) (). () () 7. () (D) 8. (C) (D) Justificaçõs:. P( )
λ, para x 0. Outras Distribuições de Probabilidade Contínuas
 abilidad Estatística I Antonio Roqu Aula 3 Outras Distribuiçõs d abilidad Contínuas Vamos agora studar mais algumas distribuiçõs d probabilidads para variávis contínuas. Distribuição Eponncial Uma variávl
abilidad Estatística I Antonio Roqu Aula 3 Outras Distribuiçõs d abilidad Contínuas Vamos agora studar mais algumas distribuiçõs d probabilidads para variávis contínuas. Distribuição Eponncial Uma variávl
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 2. < arg z < π}.
 Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR LOGARITMOS E INTEGRAÇÃO DE FUNÇÕES COMPLEXAS Logaritmos () Para cada um dos sguints conjuntos
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR LOGARITMOS E INTEGRAÇÃO DE FUNÇÕES COMPLEXAS Logaritmos () Para cada um dos sguints conjuntos
r = (x 2 + y 2 ) 1 2 θ = arctan y x
 Sção 0: Equação d Laplac m coordnadas polars Laplaciano m coordnadas polars. Sja u = ux, y uma função d duas variávis. Dpndndo da rgião m qu a função stja dfinida, pod sr mais fácil trabalhar com coordnadas
Sção 0: Equação d Laplac m coordnadas polars Laplaciano m coordnadas polars. Sja u = ux, y uma função d duas variávis. Dpndndo da rgião m qu a função stja dfinida, pod sr mais fácil trabalhar com coordnadas
Cálculo IV EP7 Tutor
 Fundação ntro d iências Educação Suprior a Distância do Estado do Rio d Janiro ntro d Educação Suprior a Distância do Estado do Rio d Janiro álculo IV EP7 Tutor Ercício 1: Us a intgral d linha para ncontrar
Fundação ntro d iências Educação Suprior a Distância do Estado do Rio d Janiro ntro d Educação Suprior a Distância do Estado do Rio d Janiro álculo IV EP7 Tutor Ercício 1: Us a intgral d linha para ncontrar
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5
 P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Agrupando num bloco a Ana, a Bruna, o Carlos, a Diana o Eduardo, o bloco os rstants st amigos prmutam
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Agrupando num bloco a Ana, a Bruna, o Carlos, a Diana o Eduardo, o bloco os rstants st amigos prmutam
Prismas VOLUME DE SÓLIDOS GEOMETRICOS: CONTEÚDOS E EXERCÍCIOS
 SECRETARIA DE SEGURANÇA PÚBLICA/SECRETARIA DE EDUCAÇÃO POLÍCIA MILITAR DO ESTADO DE GOIÁS COMANDO DE ENSINO POLICIAL MILITAR COLÉGIO DA POLÍCIA MILITAR UNIDADE SARGENTO NADER ALVES DOS SANTOS SÉRIE: º
SECRETARIA DE SEGURANÇA PÚBLICA/SECRETARIA DE EDUCAÇÃO POLÍCIA MILITAR DO ESTADO DE GOIÁS COMANDO DE ENSINO POLICIAL MILITAR COLÉGIO DA POLÍCIA MILITAR UNIDADE SARGENTO NADER ALVES DOS SANTOS SÉRIE: º
Prova de Conhecimentos Específicos. 1 a QUESTÃO: (1,5 ponto) PROAC / COSEAC - Gabarito. Considere a função f definida por. f(x)=.
 Prova d Conhcimntos Espcíficos 1 a QUESTÃO: (1,5 ponto) Considr a função f dfinida por Dtrmin: -x f(x). a) as quaçõs das assíntotas horizontais vrticais, caso xistam; b) as coordnadas dos pontos d máximo
Prova d Conhcimntos Espcíficos 1 a QUESTÃO: (1,5 ponto) Considr a função f dfinida por Dtrmin: -x f(x). a) as quaçõs das assíntotas horizontais vrticais, caso xistam; b) as coordnadas dos pontos d máximo
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO INSTITUTO DE FÍSICA FÍSICA III (FIM230) /1 GABARITO DA PROVA FINAL UNIFICADA DATA: 03/07/2009
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO INSTITUTO DE FÍSICA FÍSICA III (FIM230) - 2009/1 GABARITO DA PROVA FINAL UNIFICADA DATA: 03/07/2009 PROBLEMA 1 (Cilindros coaxiais) [ 2,5 ponto(s)] Um cilindro condutor
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO INSTITUTO DE FÍSICA FÍSICA III (FIM230) - 2009/1 GABARITO DA PROVA FINAL UNIFICADA DATA: 03/07/2009 PROBLEMA 1 (Cilindros coaxiais) [ 2,5 ponto(s)] Um cilindro condutor
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 11º ANO DE ESCOLARIDADE DE MATEMÁTICA A
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Ficha d rvisão nº 5 ª Part. Para um crto valor d a para um crto valor d b a prssão ( ) gráfico stá parcialmnt rprsntado na
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Ficha d rvisão nº 5 ª Part. Para um crto valor d a para um crto valor d b a prssão ( ) gráfico stá parcialmnt rprsntado na
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES
 PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
Análise Matemática IV
 Anális Matmática IV Problmas para as Aulas Práticas Smana 7 1. Dtrmin a solução da quação difrncial d y d t = t2 + 3y 2 2ty, t > 0 qu vrifica a condição inicial y(1) = 1 indiqu o intrvalo máximo d dfinição
Anális Matmática IV Problmas para as Aulas Práticas Smana 7 1. Dtrmin a solução da quação difrncial d y d t = t2 + 3y 2 2ty, t > 0 qu vrifica a condição inicial y(1) = 1 indiqu o intrvalo máximo d dfinição
Proposta de teste de avaliação
 Proposta d tst d avaliação Matmática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Cadrno (é prmitido o uso d calculadora) Na rsposta aos itns d scolha múltipla, slcion a opção corrta. Escrva, na
Proposta d tst d avaliação Matmática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Cadrno (é prmitido o uso d calculadora) Na rsposta aos itns d scolha múltipla, slcion a opção corrta. Escrva, na
Matemática Aplicada Geoprocessamento/Professor: Lourenço Gonçalves LISTA-1 (03/04/2009)
 Matmática Aplicada Goprocssamnto/Profssor: Lournço Gonçalvs LISTA-1 (3/4/29) Exrcício-1 Considr as figuras abaixo rsponda o qu s pd. a) Qual a razão ntr as dimnsõs dos sus comprimntos? b) S o carro grand
Matmática Aplicada Goprocssamnto/Profssor: Lournço Gonçalvs LISTA-1 (3/4/29) Exrcício-1 Considr as figuras abaixo rsponda o qu s pd. a) Qual a razão ntr as dimnsõs dos sus comprimntos? b) S o carro grand
Gabarito - Colégio Naval 2015/2016 Matemática Prova Amarela
 Gabarito - Colégio Naval 05/06 Profssors: Carlos Eduardo (Cadu) André Flip Bruno Pdra Rafal Sabino Gilbrto Gil QUESTÃO Dada a inquação, podmos rscrvê-la, a partir do Torma d Bolzano, concluímos: 5 0 0
Gabarito - Colégio Naval 05/06 Profssors: Carlos Eduardo (Cadu) André Flip Bruno Pdra Rafal Sabino Gilbrto Gil QUESTÃO Dada a inquação, podmos rscrvê-la, a partir do Torma d Bolzano, concluímos: 5 0 0
MATRIZES. Matriz é uma tabela de números formada por m linhas e n colunas. Dizemos que essa matriz tem ordem m x n (lê-se: m por n), com m, n N*
 MTRIZES DEFINIÇÃO: Mtriz é um tl d númros formd por m linhs n coluns. Dizmos qu ss mtriz tm ordm m n (lê-s: m por n), com m, n N* Grlmnt dispomos os lmntos d um mtriz ntr prêntss ou ntr colchts. m m m
MTRIZES DEFINIÇÃO: Mtriz é um tl d númros formd por m linhs n coluns. Dizmos qu ss mtriz tm ordm m n (lê-s: m por n), com m, n N* Grlmnt dispomos os lmntos d um mtriz ntr prêntss ou ntr colchts. m m m
Seja f uma função r.v.r. de domínio D e seja a R um ponto de acumulação de
 p-p8 : Continuidad d funçõs rais d variávl ral. Lr atntamnt. Dominar os concitos. Fazr rcícios. Função contínua, prolongávl por continuidad, dscontínua. Classificação d dscontinuidads. Continuidad num
p-p8 : Continuidad d funçõs rais d variávl ral. Lr atntamnt. Dominar os concitos. Fazr rcícios. Função contínua, prolongávl por continuidad, dscontínua. Classificação d dscontinuidads. Continuidad num
CAPÍTULO 12 REGRA DA CADEIA
 CAPÍTULO 12 REGRA DA CADEIA 121 Introdução Em aulas passadas, aprndmos a rgra da cadia para o caso particular m qu s faz a composição ntr uma função scalar d várias variávis f uma função vtorial d uma
CAPÍTULO 12 REGRA DA CADEIA 121 Introdução Em aulas passadas, aprndmos a rgra da cadia para o caso particular m qu s faz a composição ntr uma função scalar d várias variávis f uma função vtorial d uma
Justifique todas as passagens
 ā Prova d Cálculo II - MAT2 - IOUSP /2/204 Nom : GABARITO N ō USP : Profssor : Oswaldo Rio Branco d Olivira Justifiqu todas as passagns Q 2 4 5 Total N. Considr a função f : R 2 R dfinida por f(x,y) =
ā Prova d Cálculo II - MAT2 - IOUSP /2/204 Nom : GABARITO N ō USP : Profssor : Oswaldo Rio Branco d Olivira Justifiqu todas as passagns Q 2 4 5 Total N. Considr a função f : R 2 R dfinida por f(x,y) =
Efeito da pressão decrescente da atmosfera com o aumento da altitude
 Efio da prssão dcrscn da amosfra com o aumno da aliud S lançarmos um projéil com uma vlocidad inicial suficinmn ala l aingirá aliuds ond o ar é mais rarfio do qu próximo à suprfíci da Trra Logo a rsisência
Efio da prssão dcrscn da amosfra com o aumno da aliud S lançarmos um projéil com uma vlocidad inicial suficinmn ala l aingirá aliuds ond o ar é mais rarfio do qu próximo à suprfíci da Trra Logo a rsisência
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ - UTFPR CAMPUS CORNÉLIO PROCÓPIO
 MINISÉRIO DA EDUCAÇÃO UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ - UFPR CAMPUS CORNÉLIO PROCÓPIO PR UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ Noçõs básicas d unçõs d várias variávis FUNÇÕES DE VARIAS VARIÁVEIS
MINISÉRIO DA EDUCAÇÃO UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ - UFPR CAMPUS CORNÉLIO PROCÓPIO PR UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ Noçõs básicas d unçõs d várias variávis FUNÇÕES DE VARIAS VARIÁVEIS
Análise Matemática IV Problemas para as Aulas Práticas
 Anális Matmática IV Problmas para as Aulas Práticas 7 d Abril d 003 Smana 1. Us as quaçõs d cauchy-rimann para dtrminar o conjunto dos pontos do plano complo ond as sguints funçõs admitm drivada calcul
Anális Matmática IV Problmas para as Aulas Práticas 7 d Abril d 003 Smana 1. Us as quaçõs d cauchy-rimann para dtrminar o conjunto dos pontos do plano complo ond as sguints funçõs admitm drivada calcul
3º) Equação do tipo = f ( y) dx Solução: 2. dy dx. 2 =. Integrando ambos os membros, dx. dx dx dy dx dy. vem: Ex: Resolva a equação 6x + 7 = 0.
 0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
A integral indefinida
 A integral indefinida Introdução Prof. Méricles Thadeu Moretti MTM/CFM/UFSC. A integração é uma operação fundamental na resolução de problemas de matemática, física e outras disciplinas, além de fazer
A integral indefinida Introdução Prof. Méricles Thadeu Moretti MTM/CFM/UFSC. A integração é uma operação fundamental na resolução de problemas de matemática, física e outras disciplinas, além de fazer
Desse modo, podemos dizer que as forças que atuam sobre a partícula que forma o pêndulo simples são P 1, P 2 e T.
 Pêndulo Simpls Um corpo suspnso por um fio, afastado da posição d quilíbrio sobr a linha vrtical qu passa plo ponto d suspnsão, abandonado, oscila. O corpo o fio formam o objto qu chamamos d pêndulo. Vamos
Pêndulo Simpls Um corpo suspnso por um fio, afastado da posição d quilíbrio sobr a linha vrtical qu passa plo ponto d suspnsão, abandonado, oscila. O corpo o fio formam o objto qu chamamos d pêndulo. Vamos
Fisica 2. k = 1/4πε 0 = 9,0 10 9 N.m 2 /C 2. 01. Uma partícula, que se move em linha reta, está sujeita à aceleração a(t), cuja variação
 Fisica 2 Valors d algumas constants físicas clração da gravidad: 10 m/s 2 Dnsidad da água: 1,0 g/cm 3 Calor spcífico da água: 1,0 cal/g C Carga do létron: 1,6 x 10-19 C Vlocidad da luz no vácuo: 3,0 x
Fisica 2 Valors d algumas constants físicas clração da gravidad: 10 m/s 2 Dnsidad da água: 1,0 g/cm 3 Calor spcífico da água: 1,0 cal/g C Carga do létron: 1,6 x 10-19 C Vlocidad da luz no vácuo: 3,0 x
Derivadas parciais de ordem superior à primeira. Teorema de Schwarz.
 Drivadas parciais d ordm suprior à primira. Torma d Scwarz. As drivadas das primiras drivadas são as sgundas drivadas assim sucssivamnt. Então, para uma unção d duas variávis podmos considrar, s istirm,
Drivadas parciais d ordm suprior à primira. Torma d Scwarz. As drivadas das primiras drivadas são as sgundas drivadas assim sucssivamnt. Então, para uma unção d duas variávis podmos considrar, s istirm,
Resolução da Prova 1 de Física Teórica Turma C2 de Engenharia Civil Período
 Rsolução da Prova d Física Tórica Turma C2 d Engnharia Civil Príodo 2005. Problma : Qustõs Dados do problma: m = 500 kg ; v i = 4; 0 m=s ;! a = 5! g d = 2 m. Trabalho ralizado por uma força constant: W
Rsolução da Prova d Física Tórica Turma C2 d Engnharia Civil Príodo 2005. Problma : Qustõs Dados do problma: m = 500 kg ; v i = 4; 0 m=s ;! a = 5! g d = 2 m. Trabalho ralizado por uma força constant: W
Identifique todas as folhas Folhas não identificadas NÃO SERÃO COTADAS. Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I
 Idntifiqu todas as folhas Folhas não idntificadas NÃO SERÃO COTADAS Faculdad d Economia Univrsidad Nova d Lisboa EXAME DE CÁLCULO I Ano Lctivo 8-9 - º Smstr Eam Final d ª Época m d Janiro 9 Duração: horas
Idntifiqu todas as folhas Folhas não idntificadas NÃO SERÃO COTADAS Faculdad d Economia Univrsidad Nova d Lisboa EXAME DE CÁLCULO I Ano Lctivo 8-9 - º Smstr Eam Final d ª Época m d Janiro 9 Duração: horas
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
 UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC200 MICROECONOMIA II PRIMEIRA PROVA (20) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC200 MICROECONOMIA II PRIMEIRA PROVA (20) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
 UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC00 MICROECONOMIA II PRIMEIRA PROVA (0) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC00 MICROECONOMIA II PRIMEIRA PROVA (0) () Para cada uma das funçõs d produção
{ : 0. Questões de resposta de escolha múltipla. Grupo I 1. ( ) D = x f x x D. Resposta: D. lim = 3, pode-se concluir que o
 Grupo I Qustõs d rsposta d scolha múltipla { : 0 f }. ( ) D = f D g f ( ) 0 [, + [. Como f tm domínio \{ 5}, é contínua f ( ) gráfico d f não admit assimptotas vrticais. 5 Rsposta: D lim =, pod-s concluir
Grupo I Qustõs d rsposta d scolha múltipla { : 0 f }. ( ) D = f D g f ( ) 0 [, + [. Como f tm domínio \{ 5}, é contínua f ( ) gráfico d f não admit assimptotas vrticais. 5 Rsposta: D lim =, pod-s concluir
18-04-2015. Sumário. Campo e potencial elétrico. Conceito de campo
 Sumário Unidad II Eltricidad Magntismo 1- - Noção d campo létrico. - Campo létrico criado por uma carga pontual stacionária. - Linhas d campo. APSA 21 Campo létrico. Campo létrico uniform. Concito d campo
Sumário Unidad II Eltricidad Magntismo 1- - Noção d campo létrico. - Campo létrico criado por uma carga pontual stacionária. - Linhas d campo. APSA 21 Campo létrico. Campo létrico uniform. Concito d campo
Atrito Fixação - Básica
 1. (Pucpr 2017) Um bloco d massa stá apoiado sobr uma msa plana horizontal prso a uma corda idal. A corda passa por uma polia idal na sua xtrmidad final xist um gancho d massa dsprzívl, conform mostra
1. (Pucpr 2017) Um bloco d massa stá apoiado sobr uma msa plana horizontal prso a uma corda idal. A corda passa por uma polia idal na sua xtrmidad final xist um gancho d massa dsprzívl, conform mostra
Universidade Federal do Rio de Janeiro INSTITUTO DE MATEMÁTICA Departamento de Matemática
 Univrsidad Fdral do Rio d Janiro INSTITUTO DE MATEMÁTICA Dpartamnto d Matmática Gabarito da 1 a prova d Gomtria difrncial - 20/09/2018 - Mônica 1. Sja α(s) uma curva rgular plana paramtrizada plo comprimnto
Univrsidad Fdral do Rio d Janiro INSTITUTO DE MATEMÁTICA Dpartamnto d Matmática Gabarito da 1 a prova d Gomtria difrncial - 20/09/2018 - Mônica 1. Sja α(s) uma curva rgular plana paramtrizada plo comprimnto
FENOMENOS DE TRANSPORTE 2 o Semestre de 2012 Prof. Maurício Fabbri 2ª SÉRIE DE EXERCÍCIOS
 FENOMENOS DE TRANSPORTE o Smstr d 0 Prof. Maurício Fabbri ª SÉRIE DE EXERCÍCIOS 0. O coficint d transfrência d calor Transport d calor por convcção O transint ponncial simpls Consrvação da nrgia Lia o
FENOMENOS DE TRANSPORTE o Smstr d 0 Prof. Maurício Fabbri ª SÉRIE DE EXERCÍCIOS 0. O coficint d transfrência d calor Transport d calor por convcção O transint ponncial simpls Consrvação da nrgia Lia o
Exercício 2. Calcule. f (x)<0 e f (x) e M 2 = f (0.5) =1.3 Logo
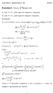 Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
NÚMEROS RACIONAIS E SUA REPRESEN- TAÇÃO FRACIONÁRIA
 NÚMEROS RACIONAIS E SUA REPRESEN- TAÇÃO FRACIONÁRIA. FRAÇÕES Com crtza todos nós já ouvimos frass como: d xícara d açúcar; d frmnto m pó tc. Basta pgar uma rcita,d bolo qu lá stão númros como sts. Ests
NÚMEROS RACIONAIS E SUA REPRESEN- TAÇÃO FRACIONÁRIA. FRAÇÕES Com crtza todos nós já ouvimos frass como: d xícara d açúcar; d frmnto m pó tc. Basta pgar uma rcita,d bolo qu lá stão númros como sts. Ests
Limite Escola Naval. Solução:
 Limit Escola Naval (EN (A 0 (B (C (D (E é igal a: ( 0 In dt r min ação, do tipo divisão por zro, log o não ist R par q pod sr tão grand qanto qisrmos, pois, M > 0, δ > 0 tal q 0 < < δ > M M A última ha
Limit Escola Naval (EN (A 0 (B (C (D (E é igal a: ( 0 In dt r min ação, do tipo divisão por zro, log o não ist R par q pod sr tão grand qanto qisrmos, pois, M > 0, δ > 0 tal q 0 < < δ > M M A última ha
Programa de Pós-Graduação Processo de Seleção 2 0 Semestre 2008 Exame de Conhecimento em Física
 UNIVERSIDADE FEDERAL DE GOIAS INSTITUTO DE FÍSICA C.P. 131, CEP 74001-970, Goiânia - Goiás - Brazil. Fon/Fax: +55 62 521-1029 Programa d Pós-Graduação Procsso d Slção 2 0 Smstr 2008 Exam d Conhcimnto m
UNIVERSIDADE FEDERAL DE GOIAS INSTITUTO DE FÍSICA C.P. 131, CEP 74001-970, Goiânia - Goiás - Brazil. Fon/Fax: +55 62 521-1029 Programa d Pós-Graduação Procsso d Slção 2 0 Smstr 2008 Exam d Conhcimnto m
c) 0 0 x y na região R limitada pelas retas y 1,
 Univrsidad Fdral d Viçosa DEPATAMENTO DE MATEMÁTIA LISTA DE EXEÍIOS - MAT ÁLULO DIFEENIAL E INTEGAL III Intgrais alcul o valor das sguints intgrais rptidas LISTA DE EXEÍIOS INTEGAIS a) ( ) d d b) d d c)
Univrsidad Fdral d Viçosa DEPATAMENTO DE MATEMÁTIA LISTA DE EXEÍIOS - MAT ÁLULO DIFEENIAL E INTEGAL III Intgrais alcul o valor das sguints intgrais rptidas LISTA DE EXEÍIOS INTEGAIS a) ( ) d d b) d d c)
Geometria Analítica - Aula
 Gomtria Analítica - Aula 0 60 K. Frnsl - J. Dlgado Aula 1 1. Rotação dos ixos coordnados Sja OXY um sistma d ixos ortogonais no plano sja O X Y o sistma d ixos obtido girando os ixos OX OY d um ângulo
Gomtria Analítica - Aula 0 60 K. Frnsl - J. Dlgado Aula 1 1. Rotação dos ixos coordnados Sja OXY um sistma d ixos ortogonais no plano sja O X Y o sistma d ixos obtido girando os ixos OX OY d um ângulo
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR A =
 Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 4 EQUAÇÕES DIFERENCIAIS LINEARES Formas canónicas d Jordan () Para cada uma das matrizs A
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 4 EQUAÇÕES DIFERENCIAIS LINEARES Formas canónicas d Jordan () Para cada uma das matrizs A
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
 REC2010 MICROECONOMIA II SEGUNDA PROVA (2011) ROBERTO GUENA (1) Considr uma indústria m concorrência prfita formada por mprsas idênticas. Para produzir, cada mprsa dv arcar com um custo quas fixo F = 1.
REC2010 MICROECONOMIA II SEGUNDA PROVA (2011) ROBERTO GUENA (1) Considr uma indústria m concorrência prfita formada por mprsas idênticas. Para produzir, cada mprsa dv arcar com um custo quas fixo F = 1.
INSTITUTO FEDERAL DA BAHIA CAMPUS JEQUIÉ LISTA DE EXERCÍCIOS DE MATEMÁTICA ALUNO:
 INSTITUTO FEDERAL DA BAHIA CAMPUS JEQUIÉ LISTA DE EXERCÍCIOS DE MATEMÁTICA ALUNO: LISTA Ciclo trigonométrico, rdução d arcos, quaçõs trigonométricas - (UFJF MG) Escrvndo os númros rais x, y, w, z y, x,
INSTITUTO FEDERAL DA BAHIA CAMPUS JEQUIÉ LISTA DE EXERCÍCIOS DE MATEMÁTICA ALUNO: LISTA Ciclo trigonométrico, rdução d arcos, quaçõs trigonométricas - (UFJF MG) Escrvndo os númros rais x, y, w, z y, x,
Ficha de Trabalho Matemática 12ºano Temas: Trigonometria ( Triângulo rectângulo e círculo trigonométrico) Proposta de correcção
 COLÉGIO PAULO VI Ficha d Trabalho Matmática ºano Tmas: Trigonomtria ( Triângulo rctângulo círculo trigonométrico) Proposta d corrcção Rlmbrar qu um radiano é, m qualqur circunfrência, a amplitud do arco
COLÉGIO PAULO VI Ficha d Trabalho Matmática ºano Tmas: Trigonomtria ( Triângulo rctângulo círculo trigonométrico) Proposta d corrcção Rlmbrar qu um radiano é, m qualqur circunfrência, a amplitud do arco
1 a Prova de F-128 Turmas do Noturno Segundo semestre de /10/2004
 1 a Prova d F-18 Turmas do Noturno Sgundo smstr d 004 18/10/004 1) Um carro s dsloca m uma avnida sgundo a quação x(t) = 0t - 5t, ond x é dado m m t m s. a) Calcul a vlocidad instantâna do carro para os
1 a Prova d F-18 Turmas do Noturno Sgundo smstr d 004 18/10/004 1) Um carro s dsloca m uma avnida sgundo a quação x(t) = 0t - 5t, ond x é dado m m t m s. a) Calcul a vlocidad instantâna do carro para os
4.1 Método das Aproximações Sucessivas ou Método de Iteração Linear (MIL)
 4. Método das Aproimaçõs Sucssivas ou Método d Itração Linar MIL O método da itração linar é um procsso itrativo qu aprsnta vantagns dsvantagns m rlação ao método da bisscção. Sja uma função f contínua
4. Método das Aproimaçõs Sucssivas ou Método d Itração Linar MIL O método da itração linar é um procsso itrativo qu aprsnta vantagns dsvantagns m rlação ao método da bisscção. Sja uma função f contínua
COLEÇÃO DARLAN MOUTINHO VOL. 04 RESOLUÇÕES. com. voce
 COLEÇÃO DARLAN MOUTINHO VOL. 04 RESOLUÇÕES RESOLUÇÃO A1 Primiramnt, dividimos a figura B m dois triângulos B1 B2, um altura d 21 m bas d 3 m outro altura bas mdindo 15 m. Mosaico 1: Tmos qu os dois triângulos
COLEÇÃO DARLAN MOUTINHO VOL. 04 RESOLUÇÕES RESOLUÇÃO A1 Primiramnt, dividimos a figura B m dois triângulos B1 B2, um altura d 21 m bas d 3 m outro altura bas mdindo 15 m. Mosaico 1: Tmos qu os dois triângulos

 Matmática A Etnsivo V. 6 Rsolva.) a) Aula. ( )
Matmática A Etnsivo V. 6 Rsolva.) a) Aula. ( )