Boa Prova! arcsen(x 2 +2x) Determine:
|
|
|
- Antônio Penha Aveiro
- 7 Há anos
- Visualizações:
Transcrição
1 Universidade Federal de Campina Grande - UFCG Centro de Ciências e Tecnologia - CCT Unidade Acadêmica de Matemática e Estatística - UAME - Tarde Prova Estágio Data: 5 de setembro de 006. Professor(a): Aluno(a): Nota:. (.0 ptos) Determine dy d, onde. y = tg 5 +. y = Boa Prova! (+) 6 arcsen( +). sec( y) = + y. (.0 ptos) Seja f() = 4 +. Encontre os intervalos onde a função f é crescente ou decrescente.. (.0 ptos) Seja y = f() uma função que satisfaz as propriedades dadas na tabela abaio. y derivadas < y < 0, y > 0 y = 0, y > 0 < < 0 y > 0, y > y > 0, y = 0 0 < < y > 0, y < 0 y = 0, y < 0 < < y < 0, y < 0 0 y < 0, y = 0 < < y < 0, y > 0 y = 0, y > 0 > y > 0, y > 0 Determine:. Os pontos críticos de f;. Os intervalos onde o gráfico da função é côncavo para baio ou côncavo para cima;. Esboce o gráfico de f. 4. (.0 ptos) Dois postes verticais de m e, 5m de altura distam m um do outro. Determine o comprimento do menor cabo que, partindo do topo de um dos postes, toque o solo e termine no topo do outro poste.(veja figura ao lado). 5. (.0 ptos) Calcule as integrais abaio. 5. ( + ) d 5. + d 5. m m sen d.,5 m 5.4 sen( ) cos( ) + sen ( ) d (sugestão: faça u = + sen ( ) )
2 Universidade Federal de Campina Grande - UFCG Centro de Ciências e Tecnologia - CCT Unidade Acadêmica de Matemática e Estatística - UAME - Manhã Prova Estágio Data: 5 de setembro de 006. Professor(a): Aluno(a): Nota:. (.0 ptos) Seja f() = 4 8. Determine:. Os pontos críticos de f; Boa Prova!. Os intervalos onde f é crescente ou decrescente;. Onde o gráfico de f é côncavo para cima e onde é côncavo para baio;.4 Os pontos de infleão de f;.5 O esboço do gráfico de f.. (.0 ptos) Derive as funções abaio. y = sen 5 (cos( )). y = arccos 4 (+). y = tg( ++ ). (.0 ptos) Pretende-se inscrever um retângulo em um triângulo retângulo isósceles cuja hipotenusa tem unidades de comprimento (Veja Figura abaio). Qual a maior área possível para o retângulo? Quais são suas dimensões? y 0 4. (.0 ptos) Calcule as integrais abaio. 5. ( 9 + ) d 5. sec(+ )tg(+ ) d, (sugestão: faça u = + ) 5. sen cos +sen d, (sugestão: faça u = sen 4 ). 5.4 d ( +)
3 Universidade Federal de Campina Grande Centro de Ciências e Tecnologia Departamento de Matemática e Estatística Professor(a): Período 007. Turno: Manhã Aluno(a): Nota: Reposição da ª Prova 0/ 07 / 007 (,5 pt.) ) Verifique se a função f:, definida por diferenciável em =. se f ( ) é se (,5 pt.) ) Determine uma equação para a reta tangente ao gráfico de f() = ² -6-4 que seja paralela a reta y = -77. (4,0 pt.) ) Calcule a derivada da função indicada e simplifique o resultado quando possível. 9 a) ( t) 5t 7. t 8 r b) h ( s) s arcsec s arctg s 4 5 c) g( ) sec 5 cos d) y. sen. y onde y é uma função de. (,5 pt.) 4) Ache uma aproimação por diferenciais para f (,0 ), onde 4 f ( ) 4 5. (,5 pt.) 5) As etremidades de um cocho de,5m de comprimento são triângulos equiláteros cujos lados têm 60 cm de comprimento. Se a água está entrando no cocho à razão de 4 l/min, determine a taa em que o nível da água está subindo quando a profundidade da água é de 0 cm.. Boa prova!
4 Universidade Federal de Campina Grande Centro de Ciências e Tecnologia Departamento de Matemática e Estatística Professor(a): Período: 007. Turno: Tarde Aluno(a): Nota: Reposição da ª Prova 0/ 07 / 007 (,5 pt) ) Use a definição de derivada de uma função, para calcular a derivada de f ( ) = em = 4. (,5 pt) )Encontre a equação da tangente a y em (,). (4,0 pt.) ) Calcule a derivada da função indicada e simplifique, sempre que possível, o resultado a) t ( t) t g b) f ( ) cot g. sec c) h ( ). arc sen d) y y, onde y é função de. (,5 pt.) 4)Um balão esférico está sendo inflado com gás. Por meio de diferenciais, aproime o aumento da área da superfície do balão quando o diâmetro varia de m para,0 m. 5 pt.) 5) Um míssil é lançado verticalmente de um ponto que está a 8 km de uma estação de rastreamento, e à mesma altura desta. Durante os primeiros 0 segundos de vôo, seu ângulo de elevação varia à razão constante de por segundo. Determine a velocidade do míssil quando o ângulo de elevação é 0. Boa prova!
5 UFCG/CAMPUS DE CAMPINA GRANDE/CCT PERÍODO: 07. Departamento de Matemática e Estatística Turno: Manhã Curso: Elétrica/Computação Aluno(a): Nota: ª. Prova 0//07 Não tire o grampo da prova e entregue todas as folhas de papel recebidas. Questão VALOR:,0 PONTOS, 0 Considere a função f ( ), 0. Esta função é diferenciável em 0? E, Em? Justifique de maneira convincente sua resposta. Questão VALOR:,0 PONTOS Determine a equação de uma reta tangente ao gráfico de f ( ) que seja paralela à reta y 4. Questão VALOR:,0 PONTOS Determine y ' em cada item a seguir: a- y 4 cos( ) e c- y 4 sin y b- y ln d- ( y ) y Questão 4 VALOR:,0 PONTOS a) Mostre que a função y ln satisfaz a equação y ' y( y ln ). b) Calcule y( 0) y'(0). Questão 5 VALOR:,0 PONTOS O volume de um balão esférico está aumentando a uma razão constante de m /min. a) Com que rapidez o raio do balão está aumentando quando este for eatamente 8 cm? b) Com que rapidez está aumentando a área superficial deste balão no mesmo instante? O único lugar onde sucesso vem antes do trabalho é no dicionário. Albert Einstein
6 Universidade Federal de Campina Grande - UFCG / CCT / UAME Data: /09/00 Aluno(a): Turno: Tarde Segunda Avaliação 00.. (,0 pts) Use a denição de derivada para calcular a derivada da função no ponto (, ). f() = + 4. (,5 pts) Calcule a derivada das seguintes funções: (a) y = cos(sen) (b) f() = sec( + 7) (c) y = ( + )e (d) f(t) = e 4 t+t (e) y = ln(θe θ ). (,5 pts) Determine a equação da reta tangente à curva quando t = π 4. C : ((t) = sec t, y(t) = tgt) 4. (,5 pts) Determine a equação da reta normal à curva y + = y 4 no ponto (, ). 5. (,0 pts) A posição de uma partícula que se desloca ao longo de uma reta coordenada é dada por s(t) = arctgt, com s em metros e t em segundos. Determine a velocidade e a aceleração da partícula para t = s. 6. (,5 pts)o comprimento l de um retângulo diminui a uma taa de cm/s, enquanto a largura w aumenta a uma taa de cm/s. Encontre as taas de variação para: a) a área; b) o perímetro; c) o comprimento da diagonal do retângulo; quando l = cm e w = 5 cm.
7 UFCG/CCT/UAME PERIODO:07. DISCIPLINA: CALCULO DIF. E INTEGRAL I TURNO: MANHA PROFº: DATA: 4//07 ALUNO(A) NOTA: º ESTÁGIO OBS: Não retire o grampo da prova. Entregue a prova com o mesmo número de folhas recebidas )(Ponto) Verifique se a função f() = 4 5 se se é derivável em =. )(Ponto) Determine, caso eistam, os pontos do gráfico de f() = cos + sen, com 0, em que a tangente é horizontal. )(4Pontos) Obtenha a derivada da função indicada e simplifique, sempre que possível o resultado: 6 a) f ( ) b) g( ) sen 6 4 c) h( ) arctg d) y cos (cos) arccos 4)(Ponto) Ache uma aproimação para f(,0) onde f() = diferenciais , usando 5)(Ponto) Ás 0 horas um carro A está 5Km ao sul do carro B. Se o carro A vai para o leste com velocidade constante de 60Km/h e o carro B vai para o norte com velocidade constante de 40Km/h, determine a razão na qual a distancia entre os carros varia ás 0:0h. 4 6)(Ponto) Verifique se a função f ( ) satisfaz as hipóteses do Teorema do Valor Médio em,4 e, em caso afirmativo, ache todos os números c em,4 tais que f b f a f c b a ( ) ( ) ( )( ). 7)(Ponto) Determine os etremos absolutos da função intervalo,, caso eistam. f ( ) no QUESTÃO OPTATIVA(Ponto) Se y é função de e satisfaz: y 6, mostre que 4 4 y 48 7 y BOA PROVA! FELIZ NATAL!
8 Universidade Federal de Campina Grande - UFCG / CCT / UAME Data: /09/00 Aluno(a): Turno: Manhã Segunda Avaliação 00.. (,0 pts) Use a denição de derivada para calcular a derivada da função no ponto (0, ). f() = +. (,5 pts) Calcule a derivada das seguintes funções: (a) y = sen( cos ) (b) f() = tg( ) (c) y = e + e (d) f() = e 4 + (e) y = ln(te t ). (,5 pts) Determine a equação da reta tangente à curva quando t = π. C : ((t) = t sent, y(t) = cos t) 4. (,5 pts) Determine a equação da reta normal à curva y 4 4y = 4 9 no ponto (, ). 5. (,0 pts) A posição de uma partícula que se desloca ao longo de uma reta coordenada é dada por s(t) = arccotgt, com s em metros e t em segundos. Determine a velocidade e a aceleração da partícula para t = s. 6. (,5 pts) O comprimento l de um retângulo diminui a uma taa de cm/s, enquanto a largura w aumenta a uma taa de cm/s. Encontre as taas de variação para: a) a área; b) o perímetro; c) o comprimento da diagonal do retângulo; quando l = cm e w = 5 cm.
9 Universidade Federal de Campina Grande - UFCG Centro de Ciências e Tecnologia CCT Unidade Acadêmica de Matemática e Estatística - UAME (Computação e Eng. Elétrica) Turno: Manhã Professor(a): Período: 009. Aluno(a): Nota: Reposição da ª Prova 0 de junho de 009 ) (,0 pt) Seja f a função definida por f ( ). a) Verifique se f é derivável em 0 = ; b) Determine a equação da reta normal ao gráfico de f no ponto (,). ) (4,0 pts) Calcule a derivada de primeira ordem das seguintes funções: a) ( ) f ; b) g ( ) log tg c) h( ) ; ; d) ( ) arc sec q. ) (,0 pts) Encontre os dois pontos onde a curva y y 7 cruza o eio e justifique que as tangentes à curva nesses pontos são paralelas. Qual é o coeficiente angular comum dessas retas? 5 ) (,0 pts) Se duas resistências com R e R ohms estão conectadas em paralelo em um circuito elétrico, resultando em uma resistência com R ohms, o valor de R é dado pela equação. R R R Se R diminui a uma taa de ohms/segundo e R aumenta a uma taa de 0,5 ohms/segundo, a que taa R varia quando R = 75 ohms e R = 50 ohms? Boa Prova e um Ótimo mês Junino
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT B33 Limites e Derivadas Prof a. Graça Luzia Dominguez Santos
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT B Limites e Derivadas Prof a Graça Luzia Dominguez Santos LISTA DE EXERCÍCIOS( Questões de Provas a UNIDADE) Derivada
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT B Limites e Derivadas Prof a Graça Luzia Dominguez Santos LISTA DE EXERCÍCIOS( Questões de Provas a UNIDADE) Derivada
MAT 141 (Turma 1) Cálculo Diferencial e Integral I 2017/II 1 a Lista de Derivadas (26/09/2017)
 Universidade Federal de Viçosa Departamento de Matemática MAT 4 (Turma ) Cálculo Diferencial e Integral I 207/II a Lista de Derivadas (26/09/207) ) Calcule f (p), usando definição de derivada. a) f() =
Universidade Federal de Viçosa Departamento de Matemática MAT 4 (Turma ) Cálculo Diferencial e Integral I 207/II a Lista de Derivadas (26/09/207) ) Calcule f (p), usando definição de derivada. a) f() =
Universidade Federal de Viçosa
 Universidade Federal de Viçosa Centro de Ciências Eatas Departamento de Matemática 3 a Lista - MAT 146 - Cálculo I 2017/I 1. Sejam f, g e h funções deriváveis. Determine [f()g()h()] e [ ] f()g(). h() 2.
Universidade Federal de Viçosa Centro de Ciências Eatas Departamento de Matemática 3 a Lista - MAT 146 - Cálculo I 2017/I 1. Sejam f, g e h funções deriváveis. Determine [f()g()h()] e [ ] f()g(). h() 2.
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
7 Derivadas e Diferenciabilidade.
 Eercícios de Cálculo p. Informática, 006-07 1 7 Derivadas e Diferenciabilidade. E 7-1 Para cada uma das funções apresentadas determine a sua derivada formando o quociente f( + h) f() h e tomando o ite
Eercícios de Cálculo p. Informática, 006-07 1 7 Derivadas e Diferenciabilidade. E 7-1 Para cada uma das funções apresentadas determine a sua derivada formando o quociente f( + h) f() h e tomando o ite
1 Definição de Derivada
 Departamento de Computação é Matemática Cálculo I USP- FFCLRP Prof. Rafael A. Rosales 5 de março de 2014 Lista 5 Derivada 1 Definição de Derivada Eercício 1. O que é f (a)? Eplique com suas palavras o
Departamento de Computação é Matemática Cálculo I USP- FFCLRP Prof. Rafael A. Rosales 5 de março de 2014 Lista 5 Derivada 1 Definição de Derivada Eercício 1. O que é f (a)? Eplique com suas palavras o
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
MAT 141 (Turma 1) Cálculo Diferencial e Integral I 2017/II 1 a Lista de Integrais (07/11/2017)
 Universidade Federal de Viçosa Departamento de Matemática MAT 4 (Turma Cálculo Diferencial e Integral I 07/II a Lista de Integrais (07//07 Faça a antidiferenciação. Verifique o resultado, calculando a
Universidade Federal de Viçosa Departamento de Matemática MAT 4 (Turma Cálculo Diferencial e Integral I 07/II a Lista de Integrais (07//07 Faça a antidiferenciação. Verifique o resultado, calculando a
MAT 140 (Cálculo I) 2017/I Lista de Derivadas e Aplicações
 Universidade Federal de Viçosa Departamento de Matemática MAT 40 (Cálculo I) 07/I Lista de Derivadas e Aplicações ) Determine a função derivada de f definida por: a) ( + 4 5) 4 b) ( 4 7 3 ) e c) ( + 4)
Universidade Federal de Viçosa Departamento de Matemática MAT 40 (Cálculo I) 07/I Lista de Derivadas e Aplicações ) Determine a função derivada de f definida por: a) ( + 4 5) 4 b) ( 4 7 3 ) e c) ( + 4)
As listas de exercícios podem ser encontradas nos seguintes endereços: ou na pasta J18, no xerox (sala1036)
 As listas de eercícios podem ser encontradas nos seguintes endereços: www.mat.ufmg.br/calculoi ou na pasta J8, no ero (sala06) TERCEIRA LISTA DE EXERCÍCIOS. Derive: a) y = 6 + b) y = c) d) y = + y = 0
As listas de eercícios podem ser encontradas nos seguintes endereços: www.mat.ufmg.br/calculoi ou na pasta J8, no ero (sala06) TERCEIRA LISTA DE EXERCÍCIOS. Derive: a) y = 6 + b) y = c) d) y = + y = 0
1. Verifique se as seguintes igualdades são válidas, seja por integração ou por. + (a + b)x3 3 + abx2 2 + c. + c. + c
 Universidade Federal de Viçosa Centro de Ciências Eatas Departamento de Matemática a Lista MAT - Cálculo I 7/II. Verifique se as seguintes igualdades são válidas, seja por integração ou por derivação:
Universidade Federal de Viçosa Centro de Ciências Eatas Departamento de Matemática a Lista MAT - Cálculo I 7/II. Verifique se as seguintes igualdades são válidas, seja por integração ou por derivação:
MAT 140 (Cálculo I) 2017/I Lista de Derivadas e Aplicações
 Universidade Federal de Viçosa Departamento de Matemática MAT 140 (Cálculo I) 2017/I Lista de Derivadas e Aplicações 1) Determine a função derivada de f definida por: a) ( 2 + 4 5) 4 b) (2 4 7 3 ) e c)
Universidade Federal de Viçosa Departamento de Matemática MAT 140 (Cálculo I) 2017/I Lista de Derivadas e Aplicações 1) Determine a função derivada de f definida por: a) ( 2 + 4 5) 4 b) (2 4 7 3 ) e c)
Matemática Exercícios
 03/0 DIFERENCIAÇÃO EM R Matemática Eercícios A. Regras de Derivação Calcular a derivada de f( considerando que toma unicamente os valores para os quais a fórmula que define f( tem significado:. f ( 3 5
03/0 DIFERENCIAÇÃO EM R Matemática Eercícios A. Regras de Derivação Calcular a derivada de f( considerando que toma unicamente os valores para os quais a fórmula que define f( tem significado:. f ( 3 5
1. O raio de uma esfera está aumentando a uma taxa de 4 mm/s. Quão rápido o volume da esfera está aumentando quando o diâmetro for 80 mm?
 MAT 001 1 ō Sem. 016 IMC UNIFEI Lista 4: Aplicações da Derivação 1. O raio de uma esfera está aumentando a uma taxa de 4 mm/s. Quão rápido o volume da esfera está aumentando quando o diâmetro for 80 mm?.
MAT 001 1 ō Sem. 016 IMC UNIFEI Lista 4: Aplicações da Derivação 1. O raio de uma esfera está aumentando a uma taxa de 4 mm/s. Quão rápido o volume da esfera está aumentando quando o diâmetro for 80 mm?.
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A
 INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A - 009. A LISTA DE EXERCÍCIOS a Questão:. Para cada uma das funções seguintes, determine as derivadas indicadas: a) f(u) = u, u() =,
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A - 009. A LISTA DE EXERCÍCIOS a Questão:. Para cada uma das funções seguintes, determine as derivadas indicadas: a) f(u) = u, u() =,
1. Calcule a derivada da função dada usando a definição. (c) f(x) = 2x + 1. (a) f(x) = 2. (b) f(x) = 5x. (d) f(x) = 2x 2 + x 1
 Lista de Eercícios de Cálculo I para os cursos de Engenharia - Derivadas 1. Calcule a derivada da função dada usando a definição. (a) f() = (b) f() = 5 (c) f() = + 1 (d) f() = + 1. O limite abaio representa
Lista de Eercícios de Cálculo I para os cursos de Engenharia - Derivadas 1. Calcule a derivada da função dada usando a definição. (a) f() = (b) f() = 5 (c) f() = + 1 (d) f() = + 1. O limite abaio representa
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT A02 CÁLCULO A ª LISTA ( QUESTÕES DE PROVAS )
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT A0 CÁLCULO A 009 ª LISTA ( QUESTÕES DE PROVAS ) Regra da cadeia ( f ( g( h(( t( )))))) f ( g( h(( t( ))))) g ( h(( t(
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT A0 CÁLCULO A 009 ª LISTA ( QUESTÕES DE PROVAS ) Regra da cadeia ( f ( g( h(( t( )))))) f ( g( h(( t( ))))) g ( h(( t(
CÁLCULO DIFERENCIAL 5-1 Para cada uma das funções apresentadas determine a sua derivada formando
 5 a Ficha de eercícios de Cálculo para Informática CÁLCULO DIFERENCIAL 5-1 Para cada uma das funções apresentadas determine a sua derivada formando o quociente f( + h) f() h e tomando o ite quando h tende
5 a Ficha de eercícios de Cálculo para Informática CÁLCULO DIFERENCIAL 5-1 Para cada uma das funções apresentadas determine a sua derivada formando o quociente f( + h) f() h e tomando o ite quando h tende
TRABALHO 1 CURSO DE VERÃO CÁLCULO I NOME DO ACADÊMICO: =, no ponto x = 2?
 TRABALHO CURSO DE VERÃO CÁLCULO I NOME DO ACADÊMICO: Questão 0 Ache a derivada das seguintes funções: 0 y 0 y 5 5 y e) y y Questão 0 Qual é a derivada da função, no ponto? Questão 0 Se, calcule () f Questão
TRABALHO CURSO DE VERÃO CÁLCULO I NOME DO ACADÊMICO: Questão 0 Ache a derivada das seguintes funções: 0 y 0 y 5 5 y e) y y Questão 0 Qual é a derivada da função, no ponto? Questão 0 Se, calcule () f Questão
3x 9. 2)lim x 3. x 4 x 2. 5) lim. 2x 3 x 2 + 7x 3 2 x + 5x 2 4x 3 9) lim sen(sen x) 11)lim 1 cosx. 18) lim. x 1 3. x 1 x 1.
 1 a Lista de Cálculo I - Escola Politécnica - 2003 Limite de Funções 1. Calcule os seguintes limites, caso eistam: 5 1) lim 0 1 2 + 56 4) lim 7 2 11 + 28 7) lim 10) lim + 1 + 1 9 + 1 13) lim tg(3) cossec(6)
1 a Lista de Cálculo I - Escola Politécnica - 2003 Limite de Funções 1. Calcule os seguintes limites, caso eistam: 5 1) lim 0 1 2 + 56 4) lim 7 2 11 + 28 7) lim 10) lim + 1 + 1 9 + 1 13) lim tg(3) cossec(6)
MAT Cálculo I - POLI a Lista de Exercícios
 MAT 453 - Cálculo I - POLI - 003 a Lista de Eercícios. Calcule a derivada indicada em cada caso: a) y se y = ; b) y se y = ( ) d ; c) ; d + ( d) d d 3 + ); e) d500 3 d 500 (3 3 79 + 4).. Calcule dy por
MAT 453 - Cálculo I - POLI - 003 a Lista de Eercícios. Calcule a derivada indicada em cada caso: a) y se y = ; b) y se y = ( ) d ; c) ; d + ( d) d d 3 + ); e) d500 3 d 500 (3 3 79 + 4).. Calcule dy por
c) R 2 e f é decrescente no intervalo 1,. , e f é crescente no intervalo 2, 2
 UFJF ICE Departamento de Matemática CÁLCULO I - LISTA DE EXERCÍCIOS Nº As questões de números a 9 referem-se à função f ( ). - O domínio da função f é o conjunto: a) R b) R c) R R, 0 e) R 0 - A derivada
UFJF ICE Departamento de Matemática CÁLCULO I - LISTA DE EXERCÍCIOS Nº As questões de números a 9 referem-se à função f ( ). - O domínio da função f é o conjunto: a) R b) R c) R R, 0 e) R 0 - A derivada
Lista de Exercícios 3 1
 Universidade Federal de Ouro Preto Departamento de Matemática MTM122 - CÁLCULO DIFERENCIAL E INTEGRAL I 1 Encontre os pontos críticos das funções a seguir: Lista de Eercícios 1 a f = + 7 2 5 b g = 7/ +
Universidade Federal de Ouro Preto Departamento de Matemática MTM122 - CÁLCULO DIFERENCIAL E INTEGRAL I 1 Encontre os pontos críticos das funções a seguir: Lista de Eercícios 1 a f = + 7 2 5 b g = 7/ +
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral I Escola Politécnica) Segunda Lista de Eercícios - Professor: Equipe de Professores EXERCÍCIOS. Calcule
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral I Escola Politécnica) Segunda Lista de Eercícios - Professor: Equipe de Professores EXERCÍCIOS. Calcule
= ; a = -1, b = 3. 1 x ; a = -1, b = 0. M > 0 é um número real fixo. Prove que quaisquer que sejam x, y em I temos f ( x) < x.
 INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA LIMITES E DERIVADAS MAT B a LISTA DE EXERCÍCIOS - 008. - Prof a Graça Luzia Dominguez Santos. Prove que entre duas raízes consecutivas de uma função
INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA LIMITES E DERIVADAS MAT B a LISTA DE EXERCÍCIOS - 008. - Prof a Graça Luzia Dominguez Santos. Prove que entre duas raízes consecutivas de uma função
Derivadas de uma Função de uma Variável
 DEPARTAMENTO DE MATEMÁTICA APLICADA - ICTE Lista CÁLCULO DIFERENCIAL E INTEGRAL I Profa.: LIDIANE SARTINI Derivadas de uma Função de uma Variável 0. Considerando que, caso eista, f (), se f() = f '( f
DEPARTAMENTO DE MATEMÁTICA APLICADA - ICTE Lista CÁLCULO DIFERENCIAL E INTEGRAL I Profa.: LIDIANE SARTINI Derivadas de uma Função de uma Variável 0. Considerando que, caso eista, f (), se f() = f '( f
MAT0146-Cálculo Diferencial e Integral I para Economia
 MAT046-Cálculo Diferencial e Integral I para Economia a Lista de Eercícios I. Limites de Funções. Calcule os seguintes limites, caso eistam: ) lim 4) lim / 7) lim 3 +9 ++4 3 +4+8 4 + 0) lim tg3) cossec6))
MAT046-Cálculo Diferencial e Integral I para Economia a Lista de Eercícios I. Limites de Funções. Calcule os seguintes limites, caso eistam: ) lim 4) lim / 7) lim 3 +9 ++4 3 +4+8 4 + 0) lim tg3) cossec6))
ln (1 + y) (x;y)!(0;0) x 2 + y 2 2) Veri que se as funções dadas são contínuas nos pontos indicados
 Governo do Estado do Rio Grande do Norte Universidade do Estado do Rio Grande do Norte Faculdade de iências Eatas e Naturais epartamento de Matemática e Estatística isciplina álculo iferencial Integral
Governo do Estado do Rio Grande do Norte Universidade do Estado do Rio Grande do Norte Faculdade de iências Eatas e Naturais epartamento de Matemática e Estatística isciplina álculo iferencial Integral
Universidade Federal de Viçosa Departamento de Matemática Centro de Ciências Exatas e Tecnológicas 5ª Lista de Exercícios de MAT140 Cálculo /2
 Universidade Federal de Viçosa Departamento de Matemática Centro de Ciências Eatas e Tecnológicas 5ª Lista de Eercícios de MAT Cálculo / ) Resolva as integrais definidas abaio a) ( + )d c) (5 ) d e) +
Universidade Federal de Viçosa Departamento de Matemática Centro de Ciências Eatas e Tecnológicas 5ª Lista de Eercícios de MAT Cálculo / ) Resolva as integrais definidas abaio a) ( + )d c) (5 ) d e) +
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A Atualizada em A LISTA DE EXERCÍCIOS
 INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A Atualizada em 007. A LISTA DE EXERCÍCIOS 0. Esboce o gráfico de f, determine f ( ), f ( ) e, caso eista, f ( ) : a a+ a, >, e a) f (
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A Atualizada em 007. A LISTA DE EXERCÍCIOS 0. Esboce o gráfico de f, determine f ( ), f ( ) e, caso eista, f ( ) : a a+ a, >, e a) f (
Exercício 1 Dê o valor, caso exista, que a função deveria assumir no ponto dado para. em p = 9
 Exercícios - Limite e Continuidade-1 Exercício 1 Dê o valor, caso exista, que a função deveria assumir no ponto dado para ser contínua: (a) f(x) = x2 16 x 4 (b) f(x) = x3 x x em p = 4 em p = 0 (c) f(x)
Exercícios - Limite e Continuidade-1 Exercício 1 Dê o valor, caso exista, que a função deveria assumir no ponto dado para ser contínua: (a) f(x) = x2 16 x 4 (b) f(x) = x3 x x em p = 4 em p = 0 (c) f(x)
x lim, sendo: 03. Considere as funções do exercício 01. Verifique se f é contínua em x = a. Justifique.
 INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A 008. A LISTA DE EXERCÍCIOS 0. Esboce o gráfico de f, determine f ( ), f ( ) e, caso eista, f ( ) : a a a, >, e a) f ( ) =, = (a = )
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A 008. A LISTA DE EXERCÍCIOS 0. Esboce o gráfico de f, determine f ( ), f ( ) e, caso eista, f ( ) : a a a, >, e a) f ( ) =, = (a = )
2a Lista de Exercícios. f (x), se x a g (x), se x < a. x 3 x, x 0, se x = 0. 1, se x 1 x 2 4 x 4, se x 1
 UFPR - Universidade Federal do Paraná Setor de Ciências Eatas Departamento de Matemática Prof. José Carlos Eidam MA/PROFMAT - Fundamentos de Cálculo a Lista de Eercícios Derivadas. Sejam f e g funções
UFPR - Universidade Federal do Paraná Setor de Ciências Eatas Departamento de Matemática Prof. José Carlos Eidam MA/PROFMAT - Fundamentos de Cálculo a Lista de Eercícios Derivadas. Sejam f e g funções
para: (a) f(x) = 3 (b) f(x) = c, c
 MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DESEMPENHO CÂMPUS PATO BRANCO Atividades Práticas Supervisionadas (APS) de Cálculo Diferencial e Integral Prof a. Dayse Batistus, Dr a.
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DESEMPENHO CÂMPUS PATO BRANCO Atividades Práticas Supervisionadas (APS) de Cálculo Diferencial e Integral Prof a. Dayse Batistus, Dr a.
UNIVERSIDADE FEDERAL DE OURO PRETO INSTITUTO DE CIÊNCIAS EXATAS E BIOLÓGICAS DEPARTAMENTO DE MATEMÁTICA
 UNIVERSIDADE FEDERAL DE OURO PRETO INSTITUTO DE CIÊNCIAS EXATAS E BIOLÓGICAS DEPARTAMENTO DE MATEMÁTICA Quarta lista de Eercícios de Cálculo Diferencial e Integral I - MTM 1 1. Nos eercícios a seguir admita
UNIVERSIDADE FEDERAL DE OURO PRETO INSTITUTO DE CIÊNCIAS EXATAS E BIOLÓGICAS DEPARTAMENTO DE MATEMÁTICA Quarta lista de Eercícios de Cálculo Diferencial e Integral I - MTM 1 1. Nos eercícios a seguir admita
Instituto de Matemática - IM/UFRJ Gabarito da Primeira Prova Unificada de Cálculo I Politécnica e Engenharia Química
 Página de 5 Questão : (3.5 pontos) Calcule: + Instituto de Matemática - IM/UFRJ Politécnica e Engenharia Química 3 2 + (a) 3 + 2 + + ; + (b) ; + (c) 0 +(sen )sen ; (d) f (), onde f() = e sen(3 + +). (a)
Página de 5 Questão : (3.5 pontos) Calcule: + Instituto de Matemática - IM/UFRJ Politécnica e Engenharia Química 3 2 + (a) 3 + 2 + + ; + (b) ; + (c) 0 +(sen )sen ; (d) f (), onde f() = e sen(3 + +). (a)
s: damasceno.
 Matemática II 6. Pro.: Luiz Gonzaga Damasceno E-mails: damasceno@yahoo.com.br damasceno@interjato.com.br damasceno@hotmail.com http://www.damasceno.ino www.damasceno.ino damasceno.ino - Derivadas Considere
Matemática II 6. Pro.: Luiz Gonzaga Damasceno E-mails: damasceno@yahoo.com.br damasceno@interjato.com.br damasceno@hotmail.com http://www.damasceno.ino www.damasceno.ino damasceno.ino - Derivadas Considere
Cálculo Diferencial e Integral 1 Lista de Exercícios Aplicação de Derivadas
 Cálculo Diferencial e Integral 1 Lista de Exercícios Aplicação de Derivadas 1) Esboce o gráfico da função f(x) = x + e responda qual é a taxa de variação média dessa função quando x varia de 0 para 4?
Cálculo Diferencial e Integral 1 Lista de Exercícios Aplicação de Derivadas 1) Esboce o gráfico da função f(x) = x + e responda qual é a taxa de variação média dessa função quando x varia de 0 para 4?
3 o quadrimestre a Lista de Exercícios - Derivadas 1 :
 Funções de Uma Variável 3 o quadrimestre - 00 a Lista de Eercícios - Derivadas : Técnicas de Derivação, Taas Relacionadas e Aplicações à Geometria Analítica. Determine o valor de a para que as funções
Funções de Uma Variável 3 o quadrimestre - 00 a Lista de Eercícios - Derivadas : Técnicas de Derivação, Taas Relacionadas e Aplicações à Geometria Analítica. Determine o valor de a para que as funções
Lista de Férias. 6 Prove a partir da definição de limite que: a) lim. (x + 6) = 9. 1 Encontre uma expressão para a função inversa: b) lim
 Lista de Férias Bases Matemáticas/FUV Encontre uma epressão para a função inversa: + 3 a) 5 2 + e b) e c) 2 + 5 d) ln( + 3) 6 Prove a partir da definição de ite que: a) 3 ( + 6) = 9 b) = c) 2 = 4 2 d)
Lista de Férias Bases Matemáticas/FUV Encontre uma epressão para a função inversa: + 3 a) 5 2 + e b) e c) 2 + 5 d) ln( + 3) 6 Prove a partir da definição de ite que: a) 3 ( + 6) = 9 b) = c) 2 = 4 2 d)
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral I (Escola Politécnica) Segunda Lista de Eercícios - Professor: Equipe de Professores EXERCÍCIOS.
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral I (Escola Politécnica) Segunda Lista de Eercícios - Professor: Equipe de Professores EXERCÍCIOS.
Lista de Exercícios 03: Derivadas e Aplicações
 Universidade Federal de Campina Grande - UFCG Centro de Ciências e Tecnologias Agroalimentar - CCTA Unidade Acadêmica de Ciências e Tecnologia Ambiental - UACTA Disciplina: Cálculo Professor: Paulo Pamplona
Universidade Federal de Campina Grande - UFCG Centro de Ciências e Tecnologias Agroalimentar - CCTA Unidade Acadêmica de Ciências e Tecnologia Ambiental - UACTA Disciplina: Cálculo Professor: Paulo Pamplona
Universidade Federal de Viçosa
 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 4 a Lista - MAT46 - Cálculo I 6/II ) Um fabricante de caixas de papelão de base quadrada deseja fazer caixas abertas
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 4 a Lista - MAT46 - Cálculo I 6/II ) Um fabricante de caixas de papelão de base quadrada deseja fazer caixas abertas
Universidade Federal de Alagoas Instituto de Matemática Curso de Graduação em Matemática. Banco de Questões
 Universidade Federal de Alagoas Instituto de Matemática Curso de Graduação em Matemática Banco de Questões Cálculo 1 Maceió, Brasil 11 de Março de 2010 Sumário 1 2005 3 1.1 1 a Avaliação-21 de fevereiro
Universidade Federal de Alagoas Instituto de Matemática Curso de Graduação em Matemática Banco de Questões Cálculo 1 Maceió, Brasil 11 de Março de 2010 Sumário 1 2005 3 1.1 1 a Avaliação-21 de fevereiro
MAT Lista de exercícios para a 3 a prova
 Universidade de São Paulo Instituto de Matemática e Estatística MAT - Lista de eercícios para a a prova Valentin Ferenczi de maio de 9. Estude a função dada com relação a máimos e mínimos locais e globais.
Universidade de São Paulo Instituto de Matemática e Estatística MAT - Lista de eercícios para a a prova Valentin Ferenczi de maio de 9. Estude a função dada com relação a máimos e mínimos locais e globais.
4.-1 Funções Deriváveis
 4.- Funções Deriváveis 4.A Em cada caso, encontre a derivada da função y = f (), usando a de nição. (a) y = + (b) y = 3 (c) y = 5 (d) y = 3 (e) y = +
4.- Funções Deriváveis 4.A Em cada caso, encontre a derivada da função y = f (), usando a de nição. (a) y = + (b) y = 3 (c) y = 5 (d) y = 3 (e) y = +
Matemática para Engenharia I. Lista Derivadas. 2. Calcule a derivada das funções abaixo nos pontos dados usando a definição:
 Matemática para Engenharia I Lista Derivadas. Usando que ( ) ( ) encontre a equação da reta tangente ao gráfico de f no ponto p(0,y 0 ). a) ( ) ( ) b) ( ), ( ) c) ( ), ( ) d) ( ), ( ( )) e) ( ), ( ) f)
Matemática para Engenharia I Lista Derivadas. Usando que ( ) ( ) encontre a equação da reta tangente ao gráfico de f no ponto p(0,y 0 ). a) ( ) ( ) b) ( ), ( ) c) ( ), ( ) d) ( ), ( ( )) e) ( ), ( ) f)
Para ilustrar o conceito de limite, vamos supor que estejamos interessados em saber o que acontece à
 Limite I) Noção intuitiva de Limite Os limites aparecem em um grande número de situações da vida real: - O zero absoluto, por eemplo, a temperatura T C na qual toda a agitação molecular cessa, é a temperatura
Limite I) Noção intuitiva de Limite Os limites aparecem em um grande número de situações da vida real: - O zero absoluto, por eemplo, a temperatura T C na qual toda a agitação molecular cessa, é a temperatura
FICHA 11 - SOLUÇÕES. b a f(x)g(x)dx b a g(x)dx M,
 Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I - o Sem 07/8 - LEGM, MEC FICHA - SOLUÇÕES a = f/; b = f; c / = f/ Começe por aplicar o Teorema de Weierstrass a f
Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I - o Sem 07/8 - LEGM, MEC FICHA - SOLUÇÕES a = f/; b = f; c / = f/ Começe por aplicar o Teorema de Weierstrass a f
Universidade Federal da Bahia
 Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 00. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 00. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
4.1 Funções Deriváveis
 4. Funções Deriváveis 4.A Em cada caso, encontre a derivada da função y = f (), usando a de nição. (a) y = + (b) y = 3 (c) y = 5 (d) y = 3 (e) y = +
4. Funções Deriváveis 4.A Em cada caso, encontre a derivada da função y = f (), usando a de nição. (a) y = + (b) y = 3 (c) y = 5 (d) y = 3 (e) y = +
DERIVADA. A Reta Tangente
 DERIVADA A Reta Tangente Seja f uma função definida numa vizinança de a. Para definir a reta tangente de uma curva = f() num ponto P(a, f(a)), consideramos um ponto vizino Q(,), em que a e traçamos a S,
DERIVADA A Reta Tangente Seja f uma função definida numa vizinança de a. Para definir a reta tangente de uma curva = f() num ponto P(a, f(a)), consideramos um ponto vizino Q(,), em que a e traçamos a S,
UNIDADE III LISTA DE EXERCÍCIOS
 Universidade Federal da Bahia Instituto de Matemática. - Departamento de Matemática. Disciplina: MATA álculo B UNIDADE III LISTA DE EXERÍIOS Atualizada. Derivada Direcional e Gradiente alcule o gradiente
Universidade Federal da Bahia Instituto de Matemática. - Departamento de Matemática. Disciplina: MATA álculo B UNIDADE III LISTA DE EXERÍIOS Atualizada. Derivada Direcional e Gradiente alcule o gradiente
Se inicialmente, o tanque estava com 100 litros, pode-se afirmar que ao final do dia o mesmo conterá.
 ANÁLISE GRÁFICA QUANDO y. CORRESPONDE A ÁREA DA FIGURA Resposta: Sempre quando o eio y corresponde a uma taa de variação, então a área compreendida entre a curva e o eio do será o produto y. Isto é y =
ANÁLISE GRÁFICA QUANDO y. CORRESPONDE A ÁREA DA FIGURA Resposta: Sempre quando o eio y corresponde a uma taa de variação, então a área compreendida entre a curva e o eio do será o produto y. Isto é y =
Exercícios sobre Trigonometria
 Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Prof Saponga uff Rua Mário Santos Braga s/n 400-40 Niterói, RJ Tels:
Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Prof Saponga uff Rua Mário Santos Braga s/n 400-40 Niterói, RJ Tels:
Estudar mudança no valor de funções na vizinhança de pontos.
 Universidade Federal de Alagoas Faculdade de Arquitetura e Urbanismo Curso de Arquitetura e Urbanismo Disciplina: Fundamentos para a Análise Estrutural Código: AURB006 Turma: A Período Letivo: 007- Professor:
Universidade Federal de Alagoas Faculdade de Arquitetura e Urbanismo Curso de Arquitetura e Urbanismo Disciplina: Fundamentos para a Análise Estrutural Código: AURB006 Turma: A Período Letivo: 007- Professor:
UNIVERSIDADE FEDERAL DE OURO PRETO INSTITUTO DE CIÊNCIAS EXATAS E BIOLÓGICAS DEPARTAMENTO DE MATEMÁTICA
 UNIVERSIDADE FEDERAL DE OURO PRETO INSTITUTO DE CIÊNCIAS EXATAS E BIOLÓGICAS DEPARTAMENTO DE MATEMÁTICA Primeira Lista de Eercícios de Cálculo Diferencial e Integral I - MTM Prof. Júlio César do Espírito
UNIVERSIDADE FEDERAL DE OURO PRETO INSTITUTO DE CIÊNCIAS EXATAS E BIOLÓGICAS DEPARTAMENTO DE MATEMÁTICA Primeira Lista de Eercícios de Cálculo Diferencial e Integral I - MTM Prof. Júlio César do Espírito
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-0 Cálculo Diferencial e Integral I (Instituto de Física) Segunda Lista de Eercícios - Professor: Aleandre Lymberopoulos. Calcule a derivada
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-0 Cálculo Diferencial e Integral I (Instituto de Física) Segunda Lista de Eercícios - Professor: Aleandre Lymberopoulos. Calcule a derivada
2. Uma escada apoiada em uma parede forma, com ela, um ângulo de 30 o. Determine o comprimento da escada, sabendo que a mesma esta a 3 m da parede:
 1. Um ciclista partindo de um ponto A, percorre 21 km para o norte; a seguir, fazendo um ângulo de 90, percorre mais 28 km para leste, chegando ao ponto B. Qual a distância, em linha reta, do ponto B ao
1. Um ciclista partindo de um ponto A, percorre 21 km para o norte; a seguir, fazendo um ângulo de 90, percorre mais 28 km para leste, chegando ao ponto B. Qual a distância, em linha reta, do ponto B ao
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-0 Cálculo Diferencial e Integral I (Instituto de Física Primeira Lista de Eercícios - Professor: Aleandre Lymberopoulos. Calcule, quando
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-0 Cálculo Diferencial e Integral I (Instituto de Física Primeira Lista de Eercícios - Professor: Aleandre Lymberopoulos. Calcule, quando
1 a LISTA DE EXERCÍCIOS DE MAT /02/2011 Professores: Rosane (Coordenadora), Allan e Cristiane. = 2x. , determine os valores de x tais que:
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA 3657-000 - VIÇOSA - MG BRASIL. Resolva as equações: a) 3 7 + b) 5 3 a LISTA DE EXERCÍCIOS DE MAT 4 8/0/0 Professores: Rosane (Coordenadora),
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA 3657-000 - VIÇOSA - MG BRASIL. Resolva as equações: a) 3 7 + b) 5 3 a LISTA DE EXERCÍCIOS DE MAT 4 8/0/0 Professores: Rosane (Coordenadora),
Universidade Federal de Viçosa
 Universidade Federal de Viçosa Ciências Eatas e Tecnológicas Departamento de Matemática MAT 4 - Lista - 07/. Determine o domínio a imagem as raízes e o estudo de sinal das funções a seguir: (a) f() = 4
Universidade Federal de Viçosa Ciências Eatas e Tecnológicas Departamento de Matemática MAT 4 - Lista - 07/. Determine o domínio a imagem as raízes e o estudo de sinal das funções a seguir: (a) f() = 4
MAT Cálculo Diferencial e Integral para Engenharia I
 MAT453 - Cálculo Diferencial e Integral para Engenharia I 1 o Semestre de 011 - a Lista de Eercícios 1. Calcule a área da região compreendida entre os gráficos de f () = 3 + 1 e g() = + 1, com 1 1.. Desenhe
MAT453 - Cálculo Diferencial e Integral para Engenharia I 1 o Semestre de 011 - a Lista de Eercícios 1. Calcule a área da região compreendida entre os gráficos de f () = 3 + 1 e g() = + 1, com 1 1.. Desenhe
MAT Cálculo Diferencial e Integral para Engenharia II 2 a lista de exercícios
 MAT454 - Cálculo Diferencial e Integral para Engenharia II a lista de exercícios - 009 1. Ache as derivadas parciais de primeira ordem das funções: ( y (a) f(x, y) = arctg (b) f(x, y) = ln(1 + cos x) (xy
MAT454 - Cálculo Diferencial e Integral para Engenharia II a lista de exercícios - 009 1. Ache as derivadas parciais de primeira ordem das funções: ( y (a) f(x, y) = arctg (b) f(x, y) = ln(1 + cos x) (xy
MAT111 - Cálculo Diferencial e Integral I - IO Prof. Gláucio Terra
 MAT - Cálculo Diferencial e Integral I - IO - 205 Prof. Gláucio Terra a Lista de Exercícios Limites de Funções. Calcule os seguintes limites, caso existam: ) lim x 3 5 x 4) lim x 8 x 2 + 0x 6 2x 2 4x 6
MAT - Cálculo Diferencial e Integral I - IO - 205 Prof. Gláucio Terra a Lista de Exercícios Limites de Funções. Calcule os seguintes limites, caso existam: ) lim x 3 5 x 4) lim x 8 x 2 + 0x 6 2x 2 4x 6
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Eatas Departamento de Matemática 3 a Lista MAT 141 - Cálculo Diferencial e Integral 016/I Professores: Filipe, Juliana, Bulmer 1. Estude a variação de
1 Universidade Federal de Viçosa Centro de Ciências Eatas Departamento de Matemática 3 a Lista MAT 141 - Cálculo Diferencial e Integral 016/I Professores: Filipe, Juliana, Bulmer 1. Estude a variação de
1ª Avaliação. lim lim lim. Resolvendo o sistema formado pelas equações (1) e (2), teremos c 3 e
 1ª Avaliação 1) Determine os limites abaio: a) lim 4 4 1 1 4 1 1 4 4 4 1 1 1 lim lim lim 4 4 4 4 4 16 4 4 4 b) 4 16 lim 4 4 4 16 lim lim lim lim 4 4 4 8 4 ) Determine os valores das constantes c e k que
1ª Avaliação 1) Determine os limites abaio: a) lim 4 4 1 1 4 1 1 4 4 4 1 1 1 lim lim lim 4 4 4 4 4 16 4 4 4 b) 4 16 lim 4 4 4 16 lim lim lim lim 4 4 4 8 4 ) Determine os valores das constantes c e k que
MAT146 - Cálculo I - FEA, Economia
 MAT46 - Cálculo I - FEA, Economia - 202 a Lista de Exercícios Limites de Funções. Calcule os seguintes limites, caso existam: 5 3x + 9 ) lim 2) lim x 3 x x 3 x + 3 x 2 + 0x 6 4) lim x 8 2x 2 4x 6 x 7)
MAT46 - Cálculo I - FEA, Economia - 202 a Lista de Exercícios Limites de Funções. Calcule os seguintes limites, caso existam: 5 3x + 9 ) lim 2) lim x 3 x x 3 x + 3 x 2 + 0x 6 4) lim x 8 2x 2 4x 6 x 7)
MAT Cálculo Diferencial e Integral para Engenharia II 1 a lista de exercícios
 MAT5 - Cálculo Diferencial e Integral para Engenharia II a lista de eercícios - 0 I - Polinômio de Talor. Utilizando o polinômio de Talor de ordem, calcule um valor aproimado e avalie o erro: (a) 8, (b)
MAT5 - Cálculo Diferencial e Integral para Engenharia II a lista de eercícios - 0 I - Polinômio de Talor. Utilizando o polinômio de Talor de ordem, calcule um valor aproimado e avalie o erro: (a) 8, (b)
MAT0146: Cálculo Diferencial e Integral I para Economia -noturno
 MAT0146: Cálculo Diferencial e Integral I para Economia -noturno P1-6/04/19 - Prova: A prova foi baseada na primeira lista de exercícios. Em particular compare: Questão 1 a) com Problema.6 da Primeira
MAT0146: Cálculo Diferencial e Integral I para Economia -noturno P1-6/04/19 - Prova: A prova foi baseada na primeira lista de exercícios. Em particular compare: Questão 1 a) com Problema.6 da Primeira
Lista 6 Gráficos: Pontos críticos, máximos e mínimos, partes crescentes e decrescentes. L Hôpital. Diferencial. Polinômio de Taylor
 Departamento de Computação é Matemática Cálculo I USP- FFCLRP Prof. Rafael A. Rosales 5 de março de 014 Lista 6 Gráficos: Pontos críticos, máimos e mínimos, partes crescentes e decrescentes. L Hôpital.
Departamento de Computação é Matemática Cálculo I USP- FFCLRP Prof. Rafael A. Rosales 5 de março de 014 Lista 6 Gráficos: Pontos críticos, máimos e mínimos, partes crescentes e decrescentes. L Hôpital.
MAT111 - Cálculo I - IO
 II - Integrais Indefinidas MAT - Cálculo I - IO - 0 a Lista de Eercícios Calcule as integrais indefinidas abaio: 7 + +. d.. tg d. 7. 0.. 6. 9... 8... 7. 0. sen cos d 8. d. + d. +d 7. d (arcsen) 0. e d.
II - Integrais Indefinidas MAT - Cálculo I - IO - 0 a Lista de Eercícios Calcule as integrais indefinidas abaio: 7 + +. d.. tg d. 7. 0.. 6. 9... 8... 7. 0. sen cos d 8. d. + d. +d 7. d (arcsen) 0. e d.
Quadro de Respostas Valor: 110 pontos Alternativa/Questão A B C D E. Rascunho
 UFJF ICE Departamento de Matemática Cálculo I Prova Opcional º Semestre Letivo de 04 9//04 FILA A Aluno (a): Matrícula: Turma: Instruções Gerais: - Preencher o quadro de respostas das questões de múltipla
UFJF ICE Departamento de Matemática Cálculo I Prova Opcional º Semestre Letivo de 04 9//04 FILA A Aluno (a): Matrícula: Turma: Instruções Gerais: - Preencher o quadro de respostas das questões de múltipla
FICHA DE TRABALHO DERIVADAS I PARTE. 1. Uma função f tem derivadas finitas à direita e à esquerda de x = 0. Então:
 FICHA DE TRABALHO DERIVADAS I PARTE. Uma função f tem derivadas finitas à direita e à esquerda de = 0. Então: (A) f tem necessariamente derivada finita em = 0; (B) f não tem com certeza derivada finita
FICHA DE TRABALHO DERIVADAS I PARTE. Uma função f tem derivadas finitas à direita e à esquerda de = 0. Então: (A) f tem necessariamente derivada finita em = 0; (B) f não tem com certeza derivada finita
1. FUNÇÕES REAIS DE VARIÁVEL REAL
 1 1 FUNÇÕES REAIS DE VARIÁVEL REAL 11 Funções trigonométricas inversas 111 As funções arco-seno e arco-cosseno Como as funções seno e cosseno não são injectivas em IR, só poderemos definir as suas funções
1 1 FUNÇÕES REAIS DE VARIÁVEL REAL 11 Funções trigonométricas inversas 111 As funções arco-seno e arco-cosseno Como as funções seno e cosseno não são injectivas em IR, só poderemos definir as suas funções
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas-CCE Departamento de Matemática
 Monitor: Renno Santos Guedes Universidade Federal de Viçosa Centro de Ciências Eatas e Tecnológicas-CCE Departamento de Matemática MAT 40-CÁLCULO Lista de Eercícios. Para a função g(), encontrar os seguintes
Monitor: Renno Santos Guedes Universidade Federal de Viçosa Centro de Ciências Eatas e Tecnológicas-CCE Departamento de Matemática MAT 40-CÁLCULO Lista de Eercícios. Para a função g(), encontrar os seguintes
Rafael A. Rosales 29 de maio de Diferencial 1. 4 l Hôpital 3. 5 Série de Taylor 3 01.
 Departamento de Computação é Matemática Cálculo I USP- FFCLRP Física Médica Rafael A. Rosales 9 de maio de 07 Sumário Diferencial Teorema do Valor Médio 3 Máimos e Mínimos. Gráficos 4 l Hôpital 3 5 Série
Departamento de Computação é Matemática Cálculo I USP- FFCLRP Física Médica Rafael A. Rosales 9 de maio de 07 Sumário Diferencial Teorema do Valor Médio 3 Máimos e Mínimos. Gráficos 4 l Hôpital 3 5 Série
Cálculo diferencial. Motivação - exemplos de aplicações à física
 Cálculo diferencial Motivação - eemplos de aplicações à física Considere-se um ponto móvel sobre um eio orientado, cuja posição em relação à origem é dada, em função do tempo, pela função s. st posição
Cálculo diferencial Motivação - eemplos de aplicações à física Considere-se um ponto móvel sobre um eio orientado, cuja posição em relação à origem é dada, em função do tempo, pela função s. st posição
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 Universidade Federal de Viçosa Centro de Ciências Eatas e Tecnológicas Departamento de Matemática MAT 040 Estudo Dirigido de Cálculo I 07/II Encontro 5 - /09/07: Eercício : Seja f a função cujo gráfico
Universidade Federal de Viçosa Centro de Ciências Eatas e Tecnológicas Departamento de Matemática MAT 040 Estudo Dirigido de Cálculo I 07/II Encontro 5 - /09/07: Eercício : Seja f a função cujo gráfico
Cálculo I - Curso de Matemática - Matutino - 6MAT005
 Cálculo I - Curso de Matemática - Matutino - 6MAT005 Prof. Ulysses Sodré - Londrina-PR, 17 de Abril de 008 - provas005.te TOME CUIDADO COM OS GRÁFICOS E DETALHES DA SUBSTITUIÇÃO UTILIZADA.....................................................................................................
Cálculo I - Curso de Matemática - Matutino - 6MAT005 Prof. Ulysses Sodré - Londrina-PR, 17 de Abril de 008 - provas005.te TOME CUIDADO COM OS GRÁFICOS E DETALHES DA SUBSTITUIÇÃO UTILIZADA.....................................................................................................
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral para Engenharia I Segunda Lista de Eercícios - Professor: Equipe da Disciplina. Calcule a derivada
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2453 Cálculo Diferencial e Integral para Engenharia I Segunda Lista de Eercícios - Professor: Equipe da Disciplina. Calcule a derivada
Universidade Federal da Bahia
 Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA3 - CÁLCULO B UNIDADE II - LISTA DE EXERCÍCIOS Atualiada 13.1 Coordenadas Polares [1] Dados os pontos P 1 (3, 5π 3 ), P ( 3, 33 ),
Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA3 - CÁLCULO B UNIDADE II - LISTA DE EXERCÍCIOS Atualiada 13.1 Coordenadas Polares [1] Dados os pontos P 1 (3, 5π 3 ), P ( 3, 33 ),
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
MAT Cálculo para Ciências Biológicas - Farmácia Prof. Gláucio Terra. 3 a Lista de Exercícios
 MAT0143 - Cálculo para Ciências Biológicas - Farmácia - 006 Prof. Gláucio Terra 3 a Lista de Eercícios 1-) Dois corredores iniciam uma corrida ao mesmo tempo e terminam empatados. Prove que em algum momento
MAT0143 - Cálculo para Ciências Biológicas - Farmácia - 006 Prof. Gláucio Terra 3 a Lista de Eercícios 1-) Dois corredores iniciam uma corrida ao mesmo tempo e terminam empatados. Prove que em algum momento
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ. 1. Use o gráfico de y = f(x) na figura em anexo para estimar o valor de f ( 2), f (1) e f (2).
 UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ 3 a Lista de Exercícios de Cálculo Diferencial e Integral I: Derivada Prof. Wellington D. Previero 1. Use o gráfico de y = f(x) na figura em anexo para estimar
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ 3 a Lista de Exercícios de Cálculo Diferencial e Integral I: Derivada Prof. Wellington D. Previero 1. Use o gráfico de y = f(x) na figura em anexo para estimar
2 o semestre de Calcule os seguintes limites, caso existam. Se não existirem, justifique por quê:
 MAT2454 - Cálculo II - POLI - 2 a Lista de Eercícios 2 o semestre de 2004. Calcule os seguintes ites, caso eistam. Se não eistirem, justifique por quê: (a) (b) (c) (d) (e) y 2 + y 2 (f) 2 y cos( 2 + y
MAT2454 - Cálculo II - POLI - 2 a Lista de Eercícios 2 o semestre de 2004. Calcule os seguintes ites, caso eistam. Se não eistirem, justifique por quê: (a) (b) (c) (d) (e) y 2 + y 2 (f) 2 y cos( 2 + y
Derivada - Parte 3 - Aplicações
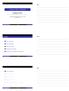 Derivada - Parte 3 - Aplicações Wellington D. Previero previero@utfpr.edu.br http://paginapessoal.utfpr.edu.br/previero Universidade Tecnológica Federal do Paraná - UTFPR Câmpus Londrina Wellington D.
Derivada - Parte 3 - Aplicações Wellington D. Previero previero@utfpr.edu.br http://paginapessoal.utfpr.edu.br/previero Universidade Tecnológica Federal do Paraná - UTFPR Câmpus Londrina Wellington D.
LISTA DE EXERCÍCIOS Valor: 0 a 1,5 Entrega em 28/novembro/2018 INTEGRAÇÃO DE FUNÇÃO REAL DE UMA VARIÁVEL REAL
 Ministério da Educação UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Câmpus Curitiba Diretoria de Graduação e Educação Profissional Departamento Acadêmico de Matemática Disciplina: Cálculo Diferencial e Integral
Ministério da Educação UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Câmpus Curitiba Diretoria de Graduação e Educação Profissional Departamento Acadêmico de Matemática Disciplina: Cálculo Diferencial e Integral
MAT Cálculo Diferencial e Integral para Engenharia II 2 a lista de exercícios
 MAT454 - Cálculo Diferencial e Integral para Engenharia II a lista de eercícios - 011 1. Ache as derivadas parciais de primeira ordem das funções: ( y (a) f(,y) = arctg (b) f(,y) = ln(1+cos ) (y 3 )).
MAT454 - Cálculo Diferencial e Integral para Engenharia II a lista de eercícios - 011 1. Ache as derivadas parciais de primeira ordem das funções: ( y (a) f(,y) = arctg (b) f(,y) = ln(1+cos ) (y 3 )).
Cálculo Diferencial e Integral I 1 o Sem. 2016/17 - LEAN, MEMat, MEQ FICHA 11 - SOLUÇÕES
 Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I o Sem 06/7 - LEAN, MEMat, MEQ FICHA - SOLUÇÕES Teorema Fundamental do Cálculo Regra de Barrow Integração por partes
Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I o Sem 06/7 - LEAN, MEMat, MEQ FICHA - SOLUÇÕES Teorema Fundamental do Cálculo Regra de Barrow Integração por partes
v m = = v(c) = s (c).
 Capítulo 17 Teorema do Valor Médio 17.1 Introdução Vimos no Cap. 16 como podemos utilizar a derivada para traçar gráficos de funções. Muito embora o apelo gráfico apresentado naquele capítulo relacionando
Capítulo 17 Teorema do Valor Médio 17.1 Introdução Vimos no Cap. 16 como podemos utilizar a derivada para traçar gráficos de funções. Muito embora o apelo gráfico apresentado naquele capítulo relacionando
Universidade Federal da Bahia
 Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 0. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 0. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
MAT Cálculo II - FEA, Economia Calcule os seguintes limites, caso existam. Se não existirem, explique por quê: xy. (i) lim.
 MAT0147 - Cálculo II - FEA, Economia - 2011 Prof. Gláucio Terra 2 a Lista de Exercícios 1. Calcule os seguintes limites, caso existam. Se não existirem, explique por quê: xy x 2 y (a) lim (f) lim (x,y)
MAT0147 - Cálculo II - FEA, Economia - 2011 Prof. Gláucio Terra 2 a Lista de Exercícios 1. Calcule os seguintes limites, caso existam. Se não existirem, explique por quê: xy x 2 y (a) lim (f) lim (x,y)
1ª Avaliação. A substituição de x por 9 leva a uma indeterminação do tipo 0/0. ( 3) ( x ) ( ) ( ) ( ) ( ) lim = lim = lim = lim. = x b x b.
 ª Avaliação ) Encontre lim 9 9. A substituição e por 9 leva a uma ineterminação o tipo 0/0. ( ) + 9 lim lim lim lim 9 9 9 9 9 9 + 9 + 9 + lim 9 ( 9 ) 9 lim + + 9 + 6 9 ( + ) se 0 < < b ) Dao f, etermine
ª Avaliação ) Encontre lim 9 9. A substituição e por 9 leva a uma ineterminação o tipo 0/0. ( ) + 9 lim lim lim lim 9 9 9 9 9 9 + 9 + 9 + lim 9 ( 9 ) 9 lim + + 9 + 6 9 ( + ) se 0 < < b ) Dao f, etermine
MAT Cálculo Diferencial e Integral para Engenharia II 2 a Lista de Exercícios
 MAT2454 - Cálculo Diferencial e Integral para Engenharia II 2 a Lista de Exercícios - 2012 1. Ache as derivadas parciais de primeira ordem das funções: ( y (a) f(x, y) = arctg (b) f(x, y) = ln(1+cos x)
MAT2454 - Cálculo Diferencial e Integral para Engenharia II 2 a Lista de Exercícios - 2012 1. Ache as derivadas parciais de primeira ordem das funções: ( y (a) f(x, y) = arctg (b) f(x, y) = ln(1+cos x)
Gabarito Primeira Prova Unificada de Cálculo /2. Engenharia e Engenharia Química. ), (1c) lim 12 x 3 x
 MUniversidade Federal do Rio de Janeiro INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Gabarito Primeira Prova Unificada de Cálculo - 0/ a Questão: Calcule: (a Engenharia e Engenharia Química 4 (,
MUniversidade Federal do Rio de Janeiro INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Gabarito Primeira Prova Unificada de Cálculo - 0/ a Questão: Calcule: (a Engenharia e Engenharia Química 4 (,
x 3 x3 dx = 1 + x2 u = 1 + x 2 5u 1 (u + 1)(u 1) du = A x ln xdx = x2 2 (ln x)2 x2 x2
 Questão -A. (, pontos) Calcule a) arctg d = arctg() 1 d = 1 + arctg() 1 u 1 6 u du = u = arctg() du = 1 dv = d v = 1+ d u = 1 + du = d = arctg() 1 1 + [u ln u ] + k = arctg() + ln(1 + ) + k. 6 6 6 b) 5e
Questão -A. (, pontos) Calcule a) arctg d = arctg() 1 d = 1 + arctg() 1 u 1 6 u du = u = arctg() du = 1 dv = d v = 1+ d u = 1 + du = d = arctg() 1 1 + [u ln u ] + k = arctg() + ln(1 + ) + k. 6 6 6 b) 5e
Cálculo I - Lista 7: Integrais II
 Faculdade de Zootecnia e Engenharia de Alimentos Universidade de São Paulo - Prof. Responsável: Andrés Vercik. Use o teorema fundamental do calculo para achar a derivada da função. g( ) = + tdt g ( ) =
Faculdade de Zootecnia e Engenharia de Alimentos Universidade de São Paulo - Prof. Responsável: Andrés Vercik. Use o teorema fundamental do calculo para achar a derivada da função. g( ) = + tdt g ( ) =
MAT Cálculo Diferencial e Integral para Engenharia II 1 a lista de exercícios
 MAT454 - Cálculo Diferencial e Integral para Engenharia II 1 a lista de exercícios - 008 POLINÔMIO DE TAYLOR 1. Utilizando o polinômio de Taylor de ordem, calcule um valor aproximado e avalie o erro: a)
MAT454 - Cálculo Diferencial e Integral para Engenharia II 1 a lista de exercícios - 008 POLINÔMIO DE TAYLOR 1. Utilizando o polinômio de Taylor de ordem, calcule um valor aproximado e avalie o erro: a)
