ActivALEA. ative e atualize a sua literacia
|
|
|
- Jerónimo Canela Paixão
- 7 Há anos
- Visualizações:
Transcrição
1 ActivALEA ative e atualize a sua literacia N.º 26 A FREQUÊNCIIA RELATIIVA PARA ESTIIMAR A PROBABIILIIDADE Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL memartins@fc.ul.pt Emília Oliveira Escola Secundária de Tomaz Pelayo ecmo.estp@gmail.com IINTRODUÇÃO O termo Probabilidade é utilizado diariamente de forma mais ou menos intuitiva, pois, nos mais variados aspetos da nossa vida, está presente a Incerteza. Nesta ActivALEA pretende-se mostrar como se pode estimar a probabilidade de um acontecimento se realizar, utilizando a frequência relativa. QUAL A PROBABILIDADE DE O Manuel frequenta o 9.º ano de escolaridade da escola básica 2,3 da Minha Terra e gosta muito da disciplina de Matemática. É mesmo a sua disciplina preferida! No entanto, nem todos os colegas têm o mesmo gosto. O Manuel gostaria de saber qual a probabilidade de, escolhido um colega da escola ao acaso, ele também preferir a Matemática. Como ajudar o Manuel a resolver esta situação?. 1/5
2 1. Introdução Antes de respondermos à questão colocada pelo Manuel, vejamos outras situações mais vulgares em que usamos o termo probabilidade. Lançando uma moeda de um euro ao ar, a probabilidade de a face Nacional ficar voltada para cima é ½. Significa que, lançando várias vezes a moeda ao ar, esperamos obter a face Nacional em 50% das vezes! Esta situação de lançar a moeda é utilizada com frequência quando temos de tomar uma decisão relativamente a duas alternativas A e B. Se não tivermos a mínima ideia sobre qual a alternativa escolher... lançamos a moeda e, se sair a face Nacional, escolhemos A; caso contrário, escolhemos B! Se em vez de uma moeda se lançar um dado de 4 faces (tetraedro) numeradas de 1 a 4, qual a probabilidade de sair a face com o número 3 quando se lança o dado? Se o dado tem 4 faces e se, à partida, não há nenhuma razão para qualquer uma das faces ser preferida, relativamente às outras, então a probabilidade de sair a face com o número 3 é ¼, ou seja, se lançarmos o dado muitas vezes espera-se que saia a face com o número 3 em 25% das vezes, pois há 4 faces todas com igual possibilidade de sair, como dissemos anteriormente. Uma situação em que este dado poderia ser útil é, por exemplo, numa questão com quatro respostas possíveis, numeradas de 1 a 4, das quais só uma é que está certa. Respondendo ao acaso, para decidir qual a resposta a escolher, poderíamos lançar o dado e, de acordo com o número saído, decidíamos qual a resposta. A probabilidade de responder corretamente seria ¼. Nos exemplos anteriores foi fácil atribuir um valor à probabilidade de sair a face Nacional ou sair a face 3, respetivamente no lançamento da moeda ou do dado de 4 faces. Mas nem sempre as situações são tão simples. Voltemos então à questão colocada inicialmente e, só para simplificar, suponhamos que cada aluno tem apenas 6 disciplinas: Língua Portuguesa (LP), Língua Estrangeira (LE), História (H), Geografia (G), Matemática (M) e Ciências Naturais (CN). O Manuel pretende averiguar a probabilidade de a Matemática ser a disciplina preferida de um colega, escolhido ao acaso. Será que, como no exemplo anterior, se poderia pegar num dado de 6 faces, escrever o nome de cada disciplina em cada uma das faces e, seguidamente, em vez de se perguntar ao aluno qual a sua disciplina preferida, lançar-se o dado e considerar-se como disciplina preferida a que estiver escrita na face que fica virada para cima? Desta forma, a probabilidade da disciplina preferida ser a Matemática (ou qualquer outra das 6 disciplinas) seria 1/6. Será que este procedimento está correto? NÃO! Só estaria correto se o aluno respondesse ao acaso, indicando uma qualquer das 6 disciplinas! Mas, na realidade, as coisas não se passam assim... As disciplinas não estão todas em igualdade de circunstâncias, pois cada aluno tem alguma ou algumas disciplinas preferidas. Vamos partir do princípio de que cada aluno tem apenas uma disciplina preferida. Então, como proceder? 2/5
3 2. A frequência relativa para estimar a probabilidade Uma vez que o procedimento anterior não está correto, uma solução será averiguar junto de alguns alunos qual a sua disciplina preferida e depois estimar a probabilidade de a disciplina favorita ser a Matemática, através da frequência relativa ou percentagem de respostas que a indicam como preferida. Por exemplo: se, numa amostra de 15 alunos, 6 deles disserem que preferem a Matemática, a frequência relativa atribuída à Matemática como disciplina preferida é de 6/15= 0,4, ou seja, 40%. Este valor obtido para a frequência relativa é considerado uma estimativa para a probabilidade de um aluno, escolhido ao acaso, preferir a Matemática. De um modo geral, estimamos a probabilidade de um determinado acontecimento se realizar pela frequência relativa com que esse acontecimento se verifica numa série de repetições da experiência, que conduza a que o acontecimento se possa realizar ou não. Na situação anterior, a realização da experiência que conduzia a que o acontecimento se realizasse ou não consistia em perguntar a um aluno escolhido ao acaso qual a disciplina favorita. O acontecimento realizava-se sempre que a resposta fosse Matemática. Esta experiência diz-se aleatória, pois, antes de fazermos a pergunta, não sabemos a resposta, embora saibamos que será uma de 6 possíveis. As respostas dos alunos inquiridos constituem a amostra utilizada para estimar a probabilidade do acontecimento a disciplina preferida é a Matemática. Ao número de respostas dadas, igual ao número de alunos inquiridos, chamamos dimensão da amostra. Se dissermos que temos um sucesso sempre que o acontecimento se realiza, então uma estimativa para a probabilidade do acontecimento se realizar é dada pela frequência relativa A estimativa será tanto melhor quanto maior for a dimensão da amostra. No caso presente, quanto mais alunos forem inquiridos, melhor será a estimativa para a probabilidade da disciplina preferida ser a Matemática. 3. Como ajudar o Manuel? Para ajudar o Manuel, o professor de Matemática decidiu planificar na turma a recolha da informação necessária para conseguir dar uma resposta à questão colocada pelo Manuel. Assim, como na escola havia 15 turmas do 9.º ano, sem contar com a turma do Manuel, o professor organizou 15 grupos (de 1 ou 2 alunos), em que cada grupo iria perguntar a 10 alunos escolhidos ao acaso, de cada uma das 15 turmas, qual a sua disciplina favorita. Para facilitar a recolha de informação, cada grupo tinha uma folha com 10 quadrados tantos 3/5
4 quantos o número de alunos a inquirir - e em cada quadrado escrevia 1 ou 0, conforme a disciplina preferida fosse a Matemática ou outra qualquer: 1.º 2.º 3.º 4.º 5.º 6.º 7.º 8.º 9.º 10.º Total Depois de todos terem feito a recolha da informação necessária, na aula iriam resumir os dados recolhidos numa tabela que o professor tinha construído para o efeito (na tabela, representa-se por sucesso a resposta Matemática ): Grupo Dim. Amostra N.º sucessos Dim amostra acumulada N.º sucessos acumulados Freq. rel. (N.º sucessos acum./dim. amostra acum) , , , , , , , , , , , , , , ,33 Se anteriormente se disse que a frequência relativa com que o acontecimento se realiza nos dá uma estimativa para a probabilidade do acontecimento se realizar, então neste momento temos 15 estimativas e não sabemos qual considerar! Sabemos sim..., pois também se disse que, quanto maior for a dimensão da amostra, melhor será a estimativa da probabilidade. Assim, a estimativa que vamos considerar para a probabilidade de um colega do Manuel preferir a Matemática é, aproximadamente, 33%. Para melhor visualizar a evolução da frequência relativa, à medida que a dimensão da amostra aumenta, podemos construir um gráfico de linhas como o que se apresenta a seguir: 4/5
5 4. Conclusão Do que se disse anteriormente, é importante fixar o seguinte: o procedimento utilizado não permite dizer que 33% é a probabilidade de um colega do Manuel, escolhido ao acaso, preferir a Matemática. O que se obteve foi um valor aproximado para essa probabilidade. Mas, então, nunca se consegue obter um valor que possamos dizer que é a probabilidade do acontecimento se realizar? Consegue-se, com algum esforço... Neste caso que estamos a analisar, teria de se perguntar a todos os colegas do Manuel qual a sua disciplina preferida e no final calcular a frequência relativa Admitindo que o total de alunos era 560 e que o número de sucessos era 196 (respostas indicando a Matemática como preferida), então a probabilidade de um aluno da escola, escolhido ao acaso, preferir a Matemática seria 0,35 (196/560) ou 35%. A frequência relativa, afinal, utiliza-se com mais frequência do que se pensa! Como, de um modo geral, a população de onde se recolhe a amostra para obter dados que nos permitam estimar a probabilidade de certo acontecimento se realizar tem dimensão grande, contentamo-nos com uma estimativa dessa probabilidade. O que temos de ter presente é que, quanto maior for a dimensão da amostra, melhor será a estimativa. Este procedimento que acabámos de descrever, em que se recolhe uma amostra e se utiliza a frequência relativa para estimar probabilidades, é o processo utilizado pelas empresas que fazem sondagens. 5/5
COMO ESTIMAR A PROBABILIDADE DE UM ACONTECIMENTO POR SIMULAÇÃO. Como estimar a probabilidade de um acontecimento por simulação
 COMO ESTIMAR A PROBABILIDADE DE UM ACONTECIMENTO POR SIMULAÇÃO Maria Eugénia Graça Martins memartins@fc.ul.pt Pretendemos com este pequeno texto dar a conhecer de uma forma simples e introdutória um processo
COMO ESTIMAR A PROBABILIDADE DE UM ACONTECIMENTO POR SIMULAÇÃO Maria Eugénia Graça Martins memartins@fc.ul.pt Pretendemos com este pequeno texto dar a conhecer de uma forma simples e introdutória um processo
ActivALEA. ative e atualize a sua literacia
 ActivALEA ative e atualize a sua literacia N.º 30 ESTIMAR A PERCENTAGEM DE... Por: Maria Eugénia Graça Martins Faculdade de Ciências da Universidade de Lisboa memartins@fc.ul.pt Emília Oliveira Agrupamento
ActivALEA ative e atualize a sua literacia N.º 30 ESTIMAR A PERCENTAGEM DE... Por: Maria Eugénia Graça Martins Faculdade de Ciências da Universidade de Lisboa memartins@fc.ul.pt Emília Oliveira Agrupamento
3º Ano do Ensino Médio. Aula nº06
 Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº06 Assunto: Noções de Estatística 1. Conceitos básicos Definição: A estatística é a ciência que recolhe, organiza, classifica, apresenta
Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº06 Assunto: Noções de Estatística 1. Conceitos básicos Definição: A estatística é a ciência que recolhe, organiza, classifica, apresenta
Proposta de teste de avaliação
 Proposta de teste de avaliação Matemática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número
Proposta de teste de avaliação Matemática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número
Introdução à Inferência Estatística
 Introdução à Inferência Estatística Prof. Cícero Quarto www.cicerocq.com Slides produzidos a partir de suas anotações de aula do curso de Especialização em Estatística, Turma 2018/UEMA, assim como, aprofundados
Introdução à Inferência Estatística Prof. Cícero Quarto www.cicerocq.com Slides produzidos a partir de suas anotações de aula do curso de Especialização em Estatística, Turma 2018/UEMA, assim como, aprofundados
Ficha de Trabalho nº 11 Matemática 7º ano Maio / 2011 INTRODUÇÃO AO ESTUDO DA ESTATÍSTICA
 Ficha de Trabalho nº 11 Matemática 7º ano Maio / 2011 INTRODUÇÃO AO ESTUDO DA ESTATÍSTICA Recorda: A Estatística é um ramo da Matemática que nos ajuda a recolher, organizar e interpretar dados para tirar
Ficha de Trabalho nº 11 Matemática 7º ano Maio / 2011 INTRODUÇÃO AO ESTUDO DA ESTATÍSTICA Recorda: A Estatística é um ramo da Matemática que nos ajuda a recolher, organizar e interpretar dados para tirar
INICIADOS - 2ª Sessão ClubeMath 7-11-2009
 INICIADOS - 2ª Sessão ClubeMath 7-11-2009 Adivinhar o dia de aniversário de outra pessoa e o mês Temos uns cartões mágicos, que vão permitir adivinhar o dia de aniversário de qualquer pessoa e outros que
INICIADOS - 2ª Sessão ClubeMath 7-11-2009 Adivinhar o dia de aniversário de outra pessoa e o mês Temos uns cartões mágicos, que vão permitir adivinhar o dia de aniversário de qualquer pessoa e outros que
Disciplinar na Adolescência: Onde está o manual de instruções?
 Disciplinar na Adolescência: Onde está o manual de instruções? Disciplinar na Adolescência: Onde está o manual de instruções? Na adolescência (autonomia, responsabilidade, relação pais filhos, regras e
Disciplinar na Adolescência: Onde está o manual de instruções? Disciplinar na Adolescência: Onde está o manual de instruções? Na adolescência (autonomia, responsabilidade, relação pais filhos, regras e
DISCIPLINA SÉRIE CAMPO CONCEITO
 Reforço escolar M ate mática Qual é a sua chance? Dinâmica 6 3ª Série 1º Bimestre DISCIPLINA SÉRIE CAMPO CONCEITO Matemática 3ª do Ensino Médio Numérico Aritmético Introdução à probabilidade Primeira Etapa
Reforço escolar M ate mática Qual é a sua chance? Dinâmica 6 3ª Série 1º Bimestre DISCIPLINA SÉRIE CAMPO CONCEITO Matemática 3ª do Ensino Médio Numérico Aritmético Introdução à probabilidade Primeira Etapa
AMEI Escolar Matemática 9º Ano Probabilidades e Estatística
 AMEI Escolar Matemática 9º Ano Probabilidades e Estatística A linguagem das probabilidades As experiências podem ser consideradas: - aleatórias ou casuais: quando é impossível calcular o resultado à partida;
AMEI Escolar Matemática 9º Ano Probabilidades e Estatística A linguagem das probabilidades As experiências podem ser consideradas: - aleatórias ou casuais: quando é impossível calcular o resultado à partida;
Testes de Hipóteses Estatísticas
 Capítulo 5 Slide 1 Testes de Hipóteses Estatísticas Resenha Hipótese nula e hipótese alternativa Erros de 1ª e 2ª espécie; potência do teste Teste a uma proporção; testes ao valor médio de uma v.a.: σ
Capítulo 5 Slide 1 Testes de Hipóteses Estatísticas Resenha Hipótese nula e hipótese alternativa Erros de 1ª e 2ª espécie; potência do teste Teste a uma proporção; testes ao valor médio de uma v.a.: σ
Probabilidade. Evento (E) é o acontecimento que deve ser analisado.
 Probabilidade Definição: Probabilidade é uma razão(divisão) entre a quantidade de eventos e a quantidade de amostras. Amostra ou espaço amostral é o conjunto formado por todos os elementos que estão incluídos
Probabilidade Definição: Probabilidade é uma razão(divisão) entre a quantidade de eventos e a quantidade de amostras. Amostra ou espaço amostral é o conjunto formado por todos os elementos que estão incluídos
Probabilidade e Estatística
 Aula 3 Professora: Rosa M. M. Leão Probabilidade e Estatística Conteúdo: 1.1 Por que estudar? 1.2 O que é? 1.3 População e Amostra 1.4 Um exemplo 1.5 Teoria da Probabilidade 1.6 Análise Combinatória 3
Aula 3 Professora: Rosa M. M. Leão Probabilidade e Estatística Conteúdo: 1.1 Por que estudar? 1.2 O que é? 1.3 População e Amostra 1.4 Um exemplo 1.5 Teoria da Probabilidade 1.6 Análise Combinatória 3
Conteúdo: Aula 2. Probabilidade e Estatística. Professora: Rosa M. M. Leão
 Aula 2 Professora: Rosa M. M. Leão Probabilidade e Estatística Conteúdo: 1.1 Por que estudar? 1.2 O que é? 1.3 População e Amostra 1.4 Um exemplo 1.5 Teoria da Probabilidade 1.6 Análise Combinatória 3
Aula 2 Professora: Rosa M. M. Leão Probabilidade e Estatística Conteúdo: 1.1 Por que estudar? 1.2 O que é? 1.3 População e Amostra 1.4 Um exemplo 1.5 Teoria da Probabilidade 1.6 Análise Combinatória 3
22 de Outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
ESCOLA SECUNDÁRIA DR. JOSÉ AFONSO
 ESCOLA SECUDÁRIA DR. JOSÉ AFOSO úcleo Gerador: Saberes Fundamentais Sociedade, Tecnologia e Ciência EFA_EF_SE1 Ano Lectivo 010/11 Ficha de Trabalho º 1 - Estatística Unidade de Competência 7 - Identificar,
ESCOLA SECUDÁRIA DR. JOSÉ AFOSO úcleo Gerador: Saberes Fundamentais Sociedade, Tecnologia e Ciência EFA_EF_SE1 Ano Lectivo 010/11 Ficha de Trabalho º 1 - Estatística Unidade de Competência 7 - Identificar,
Conceitos básicos: Variável Aleatória
 : Variável Aleatória Variável aleatória (v.a.) valor numérico que é resultado de uma eperiência aleatória. Podemos ter variáveis aleatórias contínuas ou discretas. Eemplo 1: Suponha que lança duas moedas
: Variável Aleatória Variável aleatória (v.a.) valor numérico que é resultado de uma eperiência aleatória. Podemos ter variáveis aleatórias contínuas ou discretas. Eemplo 1: Suponha que lança duas moedas
15.053 26 de fevereiro de 2002
 15.053 26 de fevereiro de 2002 Análise de Sensibilidade apresentado como Perguntas Freqüentes Pontos ilustrados em um exemplo contínuo de fabricação de garrafas. Se o tempo permitir, também consideraremos
15.053 26 de fevereiro de 2002 Análise de Sensibilidade apresentado como Perguntas Freqüentes Pontos ilustrados em um exemplo contínuo de fabricação de garrafas. Se o tempo permitir, também consideraremos
ActivALEA. active e actualize a sua literacia
 ActivALEA active e actualize a sua literacia N.º 8 PROBABIILIIDADE: PROBLEMAS E SIIMULAÇÕES A probabilidade está presente sempre que estivermos perante um fenómeno aleatório, isto é, um fenómeno para o
ActivALEA active e actualize a sua literacia N.º 8 PROBABIILIIDADE: PROBLEMAS E SIIMULAÇÕES A probabilidade está presente sempre que estivermos perante um fenómeno aleatório, isto é, um fenómeno para o
Amostragem e distribuições por amostragem
 Amostragem e distribuições por amostragem Carla Henriques e Nuno Bastos Departamento de Matemática Escola Superior de Tecnologia de Viseu Contabilidade e Administração População, amostra e inferência estatística
Amostragem e distribuições por amostragem Carla Henriques e Nuno Bastos Departamento de Matemática Escola Superior de Tecnologia de Viseu Contabilidade e Administração População, amostra e inferência estatística
I-OBJETIVO DO JOGO ENQUANTO ATIVIDADE DE ENSINO
 6 I-OBJETIVO DO JOGO ENQUANTO ATIVIDADE DE ENSINO Resolver problemas envolvendo as operações: adição subtração e multiplicação; Desenvolver a habilidade de cálculo mental. II-MATERIAL 1. Fichas com a figura
6 I-OBJETIVO DO JOGO ENQUANTO ATIVIDADE DE ENSINO Resolver problemas envolvendo as operações: adição subtração e multiplicação; Desenvolver a habilidade de cálculo mental. II-MATERIAL 1. Fichas com a figura
Probabilidade Condicional
 18 Probabilidade Condicional Sumário 18.1 Introdução....................... 2 18.2 Probabilidade Condicional............... 2 1 Unidade 18 Introdução 18.1 Introdução Nessa unidade, é apresentada mais uma
18 Probabilidade Condicional Sumário 18.1 Introdução....................... 2 18.2 Probabilidade Condicional............... 2 1 Unidade 18 Introdução 18.1 Introdução Nessa unidade, é apresentada mais uma
ESCOLA SECUNDÁRIA DA RAMADA. Teste de Matemática A. 28 de outubro de º E. Grupo I
 ESCOLA SECUNDÁRIA DA RAMADA Teste de Matemática A 28 de outubro de 206 2º E Versão Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas, são indicadas quatro alternativas,
ESCOLA SECUNDÁRIA DA RAMADA Teste de Matemática A 28 de outubro de 206 2º E Versão Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas, são indicadas quatro alternativas,
DEPARTAMENTO DE MATEMÁTICA
 FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Campus de Lhanguene, Av. de Moçambique, km 1, Tel: +258 21401078, Fax: +258 21401082, Maputo Cursos de Licenciatura em Ensino de Matemática
FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Campus de Lhanguene, Av. de Moçambique, km 1, Tel: +258 21401078, Fax: +258 21401082, Maputo Cursos de Licenciatura em Ensino de Matemática
Probabilidade. Luiz Carlos Terra
 Luiz Carlos Terra Nesta aula, você conhecerá os conceitos básicos de probabilidade que é a base de toda inferência estatística, ou seja, a estimativa de parâmetros populacionais com base em dados amostrais.
Luiz Carlos Terra Nesta aula, você conhecerá os conceitos básicos de probabilidade que é a base de toda inferência estatística, ou seja, a estimativa de parâmetros populacionais com base em dados amostrais.
ORGANIZAÇÃO E TRATAMENTO DE DADOS
 ORGANIZAÇÃO E TRATAMENTO DE DADOS Principles and Standards for School Mathematics (2000) Este documento reforça a ênfase dada no anterior documento, da importância e da adequabilidade, às crianças mais
ORGANIZAÇÃO E TRATAMENTO DE DADOS Principles and Standards for School Mathematics (2000) Este documento reforça a ênfase dada no anterior documento, da importância e da adequabilidade, às crianças mais
TRABALHO DE PESQUISA PASSO A PASSO
 3011 Ano Letivo 20-2016 TRABALHO DE PESQUISA PASSO A PASSO Uma ajuda a alunos e professores para o tratamento da informação 5º, 6º, 7º e 8º e 9º Anos de escolaridade Amélia Macedo & Bernardete Esteves
3011 Ano Letivo 20-2016 TRABALHO DE PESQUISA PASSO A PASSO Uma ajuda a alunos e professores para o tratamento da informação 5º, 6º, 7º e 8º e 9º Anos de escolaridade Amélia Macedo & Bernardete Esteves
Testes de Hipóteses. Henrique Dantas Neder
 Testes de Hipóteses Henrique Dantas Neder Vimos no capítulo anterior como construir intervalos de conança para parâmetros da população. Um outro procedimento muito utilizado em inferência é o estabelecimento
Testes de Hipóteses Henrique Dantas Neder Vimos no capítulo anterior como construir intervalos de conança para parâmetros da população. Um outro procedimento muito utilizado em inferência é o estabelecimento
I - Certezas e incertezas
 I - Certezas e incertezas Pedir aos alunos que identifiquem os acontecimentos abaixo descritos que podem ser classificados como certos, possíveis e impossíveis. O Inverno vem a seguir ao Outono. Amanhã
I - Certezas e incertezas Pedir aos alunos que identifiquem os acontecimentos abaixo descritos que podem ser classificados como certos, possíveis e impossíveis. O Inverno vem a seguir ao Outono. Amanhã
Escola Secundária/2,3 da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 2011/12 Distribuição de probabilidades 12.º Ano
 Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
4. Seja A o acontecimento associado a uma experiência aleatória em que o espaço amostral é Quais as igualdades necessariamente falsas?
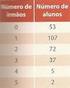
 mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais
 MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Uma pessoa lança um dado cúbico, com as faces numeradas de 1 a 6, e regista o número da face que ficou
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Uma pessoa lança um dado cúbico, com as faces numeradas de 1 a 6, e regista o número da face que ficou
Registo Escrito de Avaliação
 CENTRO DE FORMAÇÃO DO SINDICATO DOS PROFESSORES DA MADEIRA Registo Escrito de Avaliação ESTRATÉGIAS DE INTERVENÇÃO E RECUPERAÇÃO PARA ALUNOS COM DIFICULDADES EM CONTEXTO ESCOLAR: DIFICULDADES COMPORTAMENTAIS
CENTRO DE FORMAÇÃO DO SINDICATO DOS PROFESSORES DA MADEIRA Registo Escrito de Avaliação ESTRATÉGIAS DE INTERVENÇÃO E RECUPERAÇÃO PARA ALUNOS COM DIFICULDADES EM CONTEXTO ESCOLAR: DIFICULDADES COMPORTAMENTAIS
Caderno 2: 55 minutos. Tolerância: 20 minutos. (não é permitido o uso de calculadora)
 Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/1.ª Fase Caderno 2: 6 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/1.ª Fase Caderno 2: 6 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
Prova Escrita de Matemática Aplicada às Ciências Sociais
 EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 139/2012, de 5 de julho Prova Escrita de Matemática Aplicada às Ciências Sociais 10.º e 11.º Anos de Escolaridade Prova 835/1.ª Fase 12 Páginas Braille
EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 139/2012, de 5 de julho Prova Escrita de Matemática Aplicada às Ciências Sociais 10.º e 11.º Anos de Escolaridade Prova 835/1.ª Fase 12 Páginas Braille
Prova Escrita de Matemática Aplicada às Ciências Sociais
 EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 139/2012, de 5 de julho Prova Escrita de Matemática Aplicada às Ciências Sociais 10.º e 11.º Anos de Escolaridade Prova 835/1.ª Fase 13 Páginas Entrelinha
EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 139/2012, de 5 de julho Prova Escrita de Matemática Aplicada às Ciências Sociais 10.º e 11.º Anos de Escolaridade Prova 835/1.ª Fase 13 Páginas Entrelinha
24 de outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
AV2 - MA 12-2011 UMA SOLUÇÃO
 Questão 1. Considere os caminhos no plano iniciados no ponto (0, 0) com deslocamentos paralelos aos eixos coordenados, sempre de uma unidade e no sentido positivo dos eixos x e y (não se descarta a possibilidade
Questão 1. Considere os caminhos no plano iniciados no ponto (0, 0) com deslocamentos paralelos aos eixos coordenados, sempre de uma unidade e no sentido positivo dos eixos x e y (não se descarta a possibilidade
ESPANHOL INIC. Ano Letivo 2013/2014 INFORMAÇÃO - PROVA DE EQUIVALÊNCIA À FREQUÊNCIA. 11º Ano de Escolaridade
 Ano Letivo 2013/2014 INFORMAÇÃO - PROVA DE EQUIVALÊNCIA À FREQUÊNCIA ESPANHOL INIC. 11º Ano de Escolaridade Prova 375 2014 Decreto-Lei nº 139/2012, de 5 de julho 1. Objeto de avaliação A prova a que esta
Ano Letivo 2013/2014 INFORMAÇÃO - PROVA DE EQUIVALÊNCIA À FREQUÊNCIA ESPANHOL INIC. 11º Ano de Escolaridade Prova 375 2014 Decreto-Lei nº 139/2012, de 5 de julho 1. Objeto de avaliação A prova a que esta
BIO-103 Biologia evolutiva
 BIO-103 Biologia evolutiva Excerto da apostila de Genética de populações para as disciplinas BIO-305 e BIO-212 (1986-2006), vários autores. EQUILÍBRIO DE HARDY-WEINBERG Um dos aspectos importantes do estudo
BIO-103 Biologia evolutiva Excerto da apostila de Genética de populações para as disciplinas BIO-305 e BIO-212 (1986-2006), vários autores. EQUILÍBRIO DE HARDY-WEINBERG Um dos aspectos importantes do estudo
Introdução à Probabilidade e à Estatística II
 Introdução à Probabilidade e à Estatística II Introdução à Inferência Estatística Capítulo 10, Estatística Básica (Bussab&Morettin, 7a Edição) Lígia Henriques-Rodrigues MAE0229 1º semestre 2018 1 / 36
Introdução à Probabilidade e à Estatística II Introdução à Inferência Estatística Capítulo 10, Estatística Básica (Bussab&Morettin, 7a Edição) Lígia Henriques-Rodrigues MAE0229 1º semestre 2018 1 / 36
Introdução à Inferência Estatística
 Introdução à Inferência Estatística Capítulo 10, Estatística Básica (Bussab&Morettin, 7a Edição) 2a AULA 02/03/2015 MAE229 - Ano letivo 2015 Lígia Henriques-Rodrigues 2a aula (02/03/2015) MAE229 1 / 16
Introdução à Inferência Estatística Capítulo 10, Estatística Básica (Bussab&Morettin, 7a Edição) 2a AULA 02/03/2015 MAE229 - Ano letivo 2015 Lígia Henriques-Rodrigues 2a aula (02/03/2015) MAE229 1 / 16
RELATÓRIO DE AVALIAÇÃO DEPARTAMENTO DE EDUCAÇÃO PRÉ ESCOLAR. Ano Letivo 2014/2015-1.º Período
 Direção-Geral dos Estabelecimentos Escolares Direção de Serviços da Região Centro RELATÓRIO DE AVALIAÇÃO DEPARTAMENTO DE EDUCAÇÃO PRÉ ESCOLAR Ano Letivo 04/05 -.º Período A Coordenadora Francisca Oliveira
Direção-Geral dos Estabelecimentos Escolares Direção de Serviços da Região Centro RELATÓRIO DE AVALIAÇÃO DEPARTAMENTO DE EDUCAÇÃO PRÉ ESCOLAR Ano Letivo 04/05 -.º Período A Coordenadora Francisca Oliveira
2. Se A e B são acontecimentos incompatíveis, a sua interseção é o conjunto vazio, pelo que
 reparar o Exame 0 06 Matemática ágina 6. nalisemos cada opção: : e não são contrários pois a sua união não é o espaço amostral. Há, ainda, bolas pretas. : e não são contrários pois a sua união não é o
reparar o Exame 0 06 Matemática ágina 6. nalisemos cada opção: : e não são contrários pois a sua união não é o espaço amostral. Há, ainda, bolas pretas. : e não são contrários pois a sua união não é o
O JOGO COMO METODOLOGIA DO ENSINO DE MATEMÁTICA (MULTIPLICAÇÃO - TABUADA)
 O JOGO COMO METODOLOGIA DO ENSINO DE MATEMÁTICA (MULTIPLICAÇÃO - TABUADA) 3º ANO Adriana da Silva Santi Coordenação Pedagógica de Matemática Piraquara Março/2015 1 JOGOS PARA O ENSINO DA MULTIPLICAÇÃO
O JOGO COMO METODOLOGIA DO ENSINO DE MATEMÁTICA (MULTIPLICAÇÃO - TABUADA) 3º ANO Adriana da Silva Santi Coordenação Pedagógica de Matemática Piraquara Março/2015 1 JOGOS PARA O ENSINO DA MULTIPLICAÇÃO
1 a a. Para a soma dos números saídos ser 0, tem que sair 0 em ambos os dados
 Página Preparar o Exame 0 0 Matemática A. O valor médio da variável aleatória X é dado por a a a a 0 a a a. Então, a a Resposta: B. O é um dos resultados possíveis para X,(X = {0,,, }) pelo que a opção
Página Preparar o Exame 0 0 Matemática A. O valor médio da variável aleatória X é dado por a a a a 0 a a a. Então, a a Resposta: B. O é um dos resultados possíveis para X,(X = {0,,, }) pelo que a opção
TESTE GLOBAL PROBABILIDADES 12.º ANO
 TESTE GLOBAL PROBABILIDADES 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / DATA: / / DURAÇÃO DO TESTE: 90 MINUTOS VERSÃO 2 Na tua folha de respostas, indica de forma legível a versão do teste. FORMULÁRIO Probabilidades
TESTE GLOBAL PROBABILIDADES 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / DATA: / / DURAÇÃO DO TESTE: 90 MINUTOS VERSÃO 2 Na tua folha de respostas, indica de forma legível a versão do teste. FORMULÁRIO Probabilidades
PROBABILIDADE E ESTATÍSTICA UNIDADE V - INTRODUÇÃO À TEORIA DAS PROBABILIDADES
 PROBABILIDADE E ESTATÍSTICA UNIDADE V - INTRODUÇÃO À TEORIA DAS PROBABILIDADES 0 1 INTRODUÇÃO A teoria das probabilidades é utilizada para determinar as chances de um experimento aleatório acontecer. 1.1
PROBABILIDADE E ESTATÍSTICA UNIDADE V - INTRODUÇÃO À TEORIA DAS PROBABILIDADES 0 1 INTRODUÇÃO A teoria das probabilidades é utilizada para determinar as chances de um experimento aleatório acontecer. 1.1
Tema Custo Fixo, Lucro e Margem de Contribuição
 Tema Custo Fixo, Lucro e Margem de Contribuição Projeto Curso Disciplina Tema Professor(a) Pós-Graduação Engenharia da Produção Custos Industriais Custo Fixo, Lucro e Margem de Contribuição Luizete Fabris
Tema Custo Fixo, Lucro e Margem de Contribuição Projeto Curso Disciplina Tema Professor(a) Pós-Graduação Engenharia da Produção Custos Industriais Custo Fixo, Lucro e Margem de Contribuição Luizete Fabris
Microeconomia II. Cursos de Economia e de Matemática Aplicada à Economia e Gestão
 Microeconomia II Cursos de Economia e de Matemática Aplicada à Economia e Gestão AULA 3.1 Introdução à Teoria das Probabilidades e da Preferência pelo Risco Isabel Mendes 2007-2008 18-03-2008 Isabel Mendes/MICRO
Microeconomia II Cursos de Economia e de Matemática Aplicada à Economia e Gestão AULA 3.1 Introdução à Teoria das Probabilidades e da Preferência pelo Risco Isabel Mendes 2007-2008 18-03-2008 Isabel Mendes/MICRO
MATEMÁTICA A - 12o Ano Probabilidades - Distribuições de probabilidades
 MATEMÁTICA A - o Ano Probabilidades - Distribuições de probabilidades Exercícios de exames e testes intermédios. A tabela de distribuição de probabilidades de uma variável aleatória X é a seguinte. x i
MATEMÁTICA A - o Ano Probabilidades - Distribuições de probabilidades Exercícios de exames e testes intermédios. A tabela de distribuição de probabilidades de uma variável aleatória X é a seguinte. x i
Noção de fenómeno aleatório e de experiência aleatória
 Muitas vezes deparamo-nos com situações de incerteza, fenómenos aleatórios, em que não se pode prever o resultado. Pelo contrário, nos fenómenos deterministas conseguimos dizer antecipadamente o que vai
Muitas vezes deparamo-nos com situações de incerteza, fenómenos aleatórios, em que não se pode prever o resultado. Pelo contrário, nos fenómenos deterministas conseguimos dizer antecipadamente o que vai
ActivALEA. active e actualize a sua literacia
 ActivALEA active e actualize a sua literacia N.º 7 - DIAGRAMA DE BARRAS O processo de organizar a informação, quer os dados sejam qualitativos ou quantitativos, consiste em, de um modo geral, começar por
ActivALEA active e actualize a sua literacia N.º 7 - DIAGRAMA DE BARRAS O processo de organizar a informação, quer os dados sejam qualitativos ou quantitativos, consiste em, de um modo geral, começar por
A POTENCIAÇÃO EM Q 0. Aladin e a lamparina mágica
 A POTENCIAÇÃO EM Q 0 Carlos Magalhães Costa Aladin e a lamparina mágica Para o 6º Ano de Escolaridade POTÊNCIAS: CÁLCULO, LEITURA E ESCRITA Aladin tinha um amigo secreto, um génio. Quando precisava dele
A POTENCIAÇÃO EM Q 0 Carlos Magalhães Costa Aladin e a lamparina mágica Para o 6º Ano de Escolaridade POTÊNCIAS: CÁLCULO, LEITURA E ESCRITA Aladin tinha um amigo secreto, um génio. Quando precisava dele
DESAFIO FINAL TODOS OS NÍVEIS
 DESAFIO FINAL TODOS OS NÍVEIS 01. (Nível 1) No planeta Zilotaskabatu, as unidades de medidas são bem diferentes das que conhecemos na Terra. A medida padrão de comprimento é o Zimetro e um de seus submúltiplos
DESAFIO FINAL TODOS OS NÍVEIS 01. (Nível 1) No planeta Zilotaskabatu, as unidades de medidas são bem diferentes das que conhecemos na Terra. A medida padrão de comprimento é o Zimetro e um de seus submúltiplos
EXAME DE MACS 2º FASE 2014/2015 = 193
 EXAME DE MACS 2º FASE 2014/2015 1. Divisor Padrão: 00+560+80+240 200 = 190 = 19 200 20 Filiais A B C D Quota Padrão 1,088 58,01 86,010 24,870 L 1 58 86 24 L(L + 1) 1,496 58,498 86,499 24,495 Quota Padrão
EXAME DE MACS 2º FASE 2014/2015 1. Divisor Padrão: 00+560+80+240 200 = 190 = 19 200 20 Filiais A B C D Quota Padrão 1,088 58,01 86,010 24,870 L 1 58 86 24 L(L + 1) 1,496 58,498 86,499 24,495 Quota Padrão
PROFMAT Exame de Qualificação Gabarito
 PROFMAT Exame de Qualificação 2012-1 Gabarito 1. (10pts) Um corpo está contido num ambiente de temperatura constante. Decorrido o tempo (em minutos), seja a diferença entre a temperatura do corpo e do
PROFMAT Exame de Qualificação 2012-1 Gabarito 1. (10pts) Um corpo está contido num ambiente de temperatura constante. Decorrido o tempo (em minutos), seja a diferença entre a temperatura do corpo e do
Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha. Integrais Triplas
 Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo erra Cunha Integrais riplas Nas primeiras aulas discutimos integrais duplas em vária regiões. Seja motivado pelas aplicações, seja apenas pelo
Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo erra Cunha Integrais riplas Nas primeiras aulas discutimos integrais duplas em vária regiões. Seja motivado pelas aplicações, seja apenas pelo
Tema do Trabalho: Acessibilidade dos Alunos aos Meios de Comunicação Realizado por: Hélder Carneiro, Hélder Silva, Carlos Ferreira, António Marques
 Tema do Trabalho: Acessibilidade dos Alunos aos Meios de Comunicação Realizado por: Hélder Carneiro, Hélder Silva, Carlos Ferreira, António Marques População e amostra Este inquérito foi realizado na Escola
Tema do Trabalho: Acessibilidade dos Alunos aos Meios de Comunicação Realizado por: Hélder Carneiro, Hélder Silva, Carlos Ferreira, António Marques População e amostra Este inquérito foi realizado na Escola
Os problemas de decisão e a Teoria da Decisão
 Os problemas de decisão e a Teoria da Decisão p. 1/23 Para que um problema seja caracterizado, é preciso que o tomador de decisão tenha, diante de si, mais de uma alternativa. A Teoria da Decisão é um
Os problemas de decisão e a Teoria da Decisão p. 1/23 Para que um problema seja caracterizado, é preciso que o tomador de decisão tenha, diante de si, mais de uma alternativa. A Teoria da Decisão é um
5 de dezembro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 5 de dezembro de 0 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 5 de dezembro de 0 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Solução. Este problema pode ser resolvido de modo análogo ao problema anterior.
 page 11 1.2 Sistema posicional de numeração 11 Solução. Este problema pode ser resolvido de modo análogo ao problema anterior. Exercício 15: Em um conjunto de 101 moedas, há 50 falsas e as demais são verdadeiras.
page 11 1.2 Sistema posicional de numeração 11 Solução. Este problema pode ser resolvido de modo análogo ao problema anterior. Exercício 15: Em um conjunto de 101 moedas, há 50 falsas e as demais são verdadeiras.
SULIMAR GOMES SILVA INTRODUÇÃO À PROBABILIDADE
 SULIMAR GOMES SILVA INTRODUÇÃO À PROBABILIDADE Trabalho apresentado ao curso de Formação Continuada da Fundação CECIERJ - Consórcio CEDERJ. Orientadora: Danubia de Araujo Machado (Tutora) Grupo 2 Série:
SULIMAR GOMES SILVA INTRODUÇÃO À PROBABILIDADE Trabalho apresentado ao curso de Formação Continuada da Fundação CECIERJ - Consórcio CEDERJ. Orientadora: Danubia de Araujo Machado (Tutora) Grupo 2 Série:
Prova Escrita de Matemática
 ESCOLA SECUNDÁRIA DE LOUSADA Prova Escrita de Matemática.º Ciclo do ensino Básico ; 7ºAno de escolaridade Duração da Prova: 90 minutos Versão 01 A PREENCHER PELO ALUNO Nome completo do aluno Nª Turma:
ESCOLA SECUNDÁRIA DE LOUSADA Prova Escrita de Matemática.º Ciclo do ensino Básico ; 7ºAno de escolaridade Duração da Prova: 90 minutos Versão 01 A PREENCHER PELO ALUNO Nome completo do aluno Nª Turma:
UM JOGO BINOMIAL 1. INTRODUÇÃO
 1. INTRODUÇÃO UM JOGO BINOMIAL São muitos os casos de aplicação, no cotidiano de cada um de nós, dos conceitos de probabilidade. Afinal, o mundo é probabilístico, não determinístico; a natureza acontece
1. INTRODUÇÃO UM JOGO BINOMIAL São muitos os casos de aplicação, no cotidiano de cada um de nós, dos conceitos de probabilidade. Afinal, o mundo é probabilístico, não determinístico; a natureza acontece
Distribuições Amostrais
 Estatística II Antonio Roque Aula Distribuições Amostrais O problema central da inferência estatística é como fazer afirmações sobre os parâmetros de uma população a partir de estatísticas obtidas de amostras
Estatística II Antonio Roque Aula Distribuições Amostrais O problema central da inferência estatística é como fazer afirmações sobre os parâmetros de uma população a partir de estatísticas obtidas de amostras
ActivALEA. active e actualize a sua literacia. TAREFA Forma da distribuição de algumas variáveis tendo em conta a. TÓPICO - Representações gráficas.
 ActivALEA active e actualize a sua literacia N..ºº 23 FORMA DA DIISTRIIBUIIÇÃO DE ALGUMAS VARIIÁVEIIS Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL memartins@fc.ul.pt
ActivALEA active e actualize a sua literacia N..ºº 23 FORMA DA DIISTRIIBUIIÇÃO DE ALGUMAS VARIIÁVEIIS Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL memartins@fc.ul.pt
22 de Outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Distribuições por Amostragem
 Distribuições por Amostragem Departamento de Matemática Escola Superior de Tecnologia de Viseu (DepMAT ESTV) Distribuições por Amostragem 2007/2008 1 / 27 Introdução: População, amostra e inferência estatística
Distribuições por Amostragem Departamento de Matemática Escola Superior de Tecnologia de Viseu (DepMAT ESTV) Distribuições por Amostragem 2007/2008 1 / 27 Introdução: População, amostra e inferência estatística
ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO
 ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO Teste 1 Matemática 9.º C Nome: n.º Data: 14/10/2016 Classificação: Professor: Instruções gerais Não é permitido o uso de corretor. É permitido a utilização
ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO Teste 1 Matemática 9.º C Nome: n.º Data: 14/10/2016 Classificação: Professor: Instruções gerais Não é permitido o uso de corretor. É permitido a utilização
GRADUAÇÃO TECNOLÓGICA EM GESTÃO DA PRODUÇÃO INDUSTRIAL GERENCIAMENTO ESTATÍSTICO DOS PROCESSOS PRODUTIVOS (tópicos da aula 3)
 1 GRADUAÇÃO TECNOLÓGICA EM GESTÃO DA PRODUÇÃO INDUSTRIAL GERENCIAMENTO ESTATÍSTICO DOS PROCESSOS PRODUTIVOS (tópicos da aula 3) ANÁLISE DO PROCESSO Só é possivel monitorar um processo após conhecê-lo bem.
1 GRADUAÇÃO TECNOLÓGICA EM GESTÃO DA PRODUÇÃO INDUSTRIAL GERENCIAMENTO ESTATÍSTICO DOS PROCESSOS PRODUTIVOS (tópicos da aula 3) ANÁLISE DO PROCESSO Só é possivel monitorar um processo após conhecê-lo bem.
Material Teórico - Módulo Probabilidade Condicional. Probabilidade Condicional - Parte 1. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Probabilidade Condicional Probabilidade Condicional - Parte 1 Segundo Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Probabilidade
Material Teórico - Módulo Probabilidade Condicional Probabilidade Condicional - Parte 1 Segundo Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Probabilidade
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Propostas de resolução
 MATEMÁTICA A - 1o Ano Probabilidades - Noções gerais Propostas de resolução Exercícios de exames e testes intermédios 1. Organizando todos os resultados possíveis para os dois números possíveis de observar,
MATEMÁTICA A - 1o Ano Probabilidades - Noções gerais Propostas de resolução Exercícios de exames e testes intermédios 1. Organizando todos os resultados possíveis para os dois números possíveis de observar,
ÁREA DO PROFESSOR (TUTOR)
 ÁREA DO PROFESSOR (TUTOR) O MOODLE (Modular Object Oriented Dynamic Learning Environment) é um Ambiente Virtual de Ensino-Aprendizagem (AVEA) de código aberto, livre e gratuito que se mantém em desenvolvimento
ÁREA DO PROFESSOR (TUTOR) O MOODLE (Modular Object Oriented Dynamic Learning Environment) é um Ambiente Virtual de Ensino-Aprendizagem (AVEA) de código aberto, livre e gratuito que se mantém em desenvolvimento
Objetivos. Expressar o vértice da parábola em termos do discriminante e dos
 MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades
 Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades Nome: Data: / / 1. Das seguintes experiências diz, justificando, quais são as aleatórias: 1.1. Deitar um berlinde num copo de água
Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades Nome: Data: / / 1. Das seguintes experiências diz, justificando, quais são as aleatórias: 1.1. Deitar um berlinde num copo de água
Prof. Eugênio Carlos Stieler
 CAPITALIZAÇÃO COMPOSTA CAPITALIZAÇÁO COMPOSTA: MONTANTE E VALOR ATUAL PARA PAGAMENTO ÚNICO Capitalização composta é aquela em que a taxa de juros incide sobre o capital inicial, acrescido dos juros acumulados
CAPITALIZAÇÃO COMPOSTA CAPITALIZAÇÁO COMPOSTA: MONTANTE E VALOR ATUAL PARA PAGAMENTO ÚNICO Capitalização composta é aquela em que a taxa de juros incide sobre o capital inicial, acrescido dos juros acumulados
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE Prof. Aurimenes A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios.
PROBABILIDADE Prof. Aurimenes A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios.
Análise Combinatória e Probabilidade
 Análise Combinatória e Probabilidade E aí, beleza!? Vamos juntos dar uma olhada em algumas dicas importantes de análise combinatória e probabilidade? Análise Combinatória Considere a seguinte situação:
Análise Combinatória e Probabilidade E aí, beleza!? Vamos juntos dar uma olhada em algumas dicas importantes de análise combinatória e probabilidade? Análise Combinatória Considere a seguinte situação:
47 = 1349 (ou multiplicando por 100 para converter para porcentagem: 3,5%).
 Probabilidade Elementar Probabilidade e Estatística I Antonio Roque Aula 9 Fundamentos A tabela a seguir apresenta freqüências associadas a classes de níveis de colesterol no soro de uma amostra de homens
Probabilidade Elementar Probabilidade e Estatística I Antonio Roque Aula 9 Fundamentos A tabela a seguir apresenta freqüências associadas a classes de níveis de colesterol no soro de uma amostra de homens
Adição de probabilidades. O número de elementos da união dos conjuntos A e B n(aub) = n(a B) Dividindo os dois membros por n(e):
 Adição de probabilidades O número de elementos da união dos conjuntos A e B n(aub) = n(a B) Dividindo os dois membros por n(e): Dois eventos A e B são ditos mutuamente exclusivos se, e somente se, A B
Adição de probabilidades O número de elementos da união dos conjuntos A e B n(aub) = n(a B) Dividindo os dois membros por n(e): Dois eventos A e B são ditos mutuamente exclusivos se, e somente se, A B
TESTES SOCIOMÉTRICOS
 TESTES SOCIOMÉTRICOS Docente: Mestre Mª João Marques da Silva Picão Oliveira TESTES SOCIOMÉTRICOS * O Teste Sociométrico ajuda-nos a avaliar o grau de integração duma criança/jovem no grupo; a descobrir
TESTES SOCIOMÉTRICOS Docente: Mestre Mª João Marques da Silva Picão Oliveira TESTES SOCIOMÉTRICOS * O Teste Sociométrico ajuda-nos a avaliar o grau de integração duma criança/jovem no grupo; a descobrir
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 3
 FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
Introdução à Privacidade
 Introdução à Privacidade Os participantes vão explorar o sentido individual de privacidade e o impacto que esta tem nas suas vidas. Os participantes vão decidir que tipo de informações preferem manter
Introdução à Privacidade Os participantes vão explorar o sentido individual de privacidade e o impacto que esta tem nas suas vidas. Os participantes vão decidir que tipo de informações preferem manter
Se A =, o evento é impossível, por exemplo, obter 7 no lançamento de um dado.
 PROBABILIDADE Espaço amostral Espaço amostral é o conjunto universo U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(u). Exemplos: No
PROBABILIDADE Espaço amostral Espaço amostral é o conjunto universo U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(u). Exemplos: No
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 1
 FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 1 Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 1 Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais
 MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Considere um dado cúbico, com as faces numeradas de 1 a 6, e um saco que contém cinco bolas, indistinguíveis
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Considere um dado cúbico, com as faces numeradas de 1 a 6, e um saco que contém cinco bolas, indistinguíveis
Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema I Probabilidades e Combinatória
 Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema I Probabilidades e Combinatória Tarefa nº 1 1. Verdadeiro ou Falso? 1.1. É pouco provável tirar um rei ao acaso de um baralho de 52
Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema I Probabilidades e Combinatória Tarefa nº 1 1. Verdadeiro ou Falso? 1.1. É pouco provável tirar um rei ao acaso de um baralho de 52
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
Agrupamento de Escolas de Diogo Cão, Vila Real
 Agrupamento de Escolas de Diogo Cão, Vila Real 2015/2016 MATEMÁTICA FICHA DE TRABALHO 7 3º PERÍODO MAIO Nome: Nº Turma: 9º Data: CIRCUNFERÊNCIA 1. Relativamente à fig. 1 indica: 1.1 duas cordas; 1.2 a
Agrupamento de Escolas de Diogo Cão, Vila Real 2015/2016 MATEMÁTICA FICHA DE TRABALHO 7 3º PERÍODO MAIO Nome: Nº Turma: 9º Data: CIRCUNFERÊNCIA 1. Relativamente à fig. 1 indica: 1.1 duas cordas; 1.2 a
Probabilidade e Estatística I Antonio Roque Aula 2. Tabelas e Diagramas de Freqüência
 Tabelas e Diagramas de Freqüência Probabilidade e Estatística I Antonio Roque Aula 2 O primeiro passo na análise e interpretação dos dados de uma amostra consiste na descrição (apresentação) dos dados
Tabelas e Diagramas de Freqüência Probabilidade e Estatística I Antonio Roque Aula 2 O primeiro passo na análise e interpretação dos dados de uma amostra consiste na descrição (apresentação) dos dados
A 'BC' e, com uma régua, obteve estas medidas:
 1 Um estudante tinha de calcular a área do triângulo ABC, mas um pedaço da folha do caderno rasgou-se. Ele, então, traçou o segmento A 'C' paralelo a AC, a altura C' H do triângulo A 'BC' e, com uma régua,
1 Um estudante tinha de calcular a área do triângulo ABC, mas um pedaço da folha do caderno rasgou-se. Ele, então, traçou o segmento A 'C' paralelo a AC, a altura C' H do triângulo A 'BC' e, com uma régua,
Distribuição Normal de Probabilidade
 Distribuição Normal de Probabilidade 1 Aspectos Gerais 2 A Distribuição Normal Padronizada 3 Determinação de Probabilidades 4 Cálculo de Valores 5 Teorema Central do Limite 1 1 Aspectos Gerais Variável
Distribuição Normal de Probabilidade 1 Aspectos Gerais 2 A Distribuição Normal Padronizada 3 Determinação de Probabilidades 4 Cálculo de Valores 5 Teorema Central do Limite 1 1 Aspectos Gerais Variável
ORAGANIZAÇÃO, REPRESENTAÇÃO E INTERPRETAÇÃO DE DADOS
 Prof. Patricia Caldana ORAGANIZAÇÃO, REPRESENTAÇÃO E INTERPRETAÇÃO DE DADOS Estatística é uma ciência exata que visa fornecer subsídios ao analista para coletar, organizar, resumir, analisar e apresentar
Prof. Patricia Caldana ORAGANIZAÇÃO, REPRESENTAÇÃO E INTERPRETAÇÃO DE DADOS Estatística é uma ciência exata que visa fornecer subsídios ao analista para coletar, organizar, resumir, analisar e apresentar
Treinamento sobre Progress Report.
 Treinamento sobre Progress Report. Objetivo O foco aqui é trabalhar o desenvolvimento pessoal de cada aluno. O instrutor irá analisar cada um e pensar em suas dificuldades e barreiras de aprendizado e,
Treinamento sobre Progress Report. Objetivo O foco aqui é trabalhar o desenvolvimento pessoal de cada aluno. O instrutor irá analisar cada um e pensar em suas dificuldades e barreiras de aprendizado e,
Tema do trabalho: Aspectos familiares e férias dos alunos Realizado por: António Freire, João Silva, João Fernandes e Norberto Feitas
 Tema do trabalho: Aspectos familiares e férias dos alunos Realizado por: António Freire, João Silva, João Fernandes e Norberto Feitas Variáveis estudadas: n.º de pessoas do agregado familiar, habilitações
Tema do trabalho: Aspectos familiares e férias dos alunos Realizado por: António Freire, João Silva, João Fernandes e Norberto Feitas Variáveis estudadas: n.º de pessoas do agregado familiar, habilitações
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
1- INTRODUÇÃO 2. CONCEITOS BÁSICOS
 1 1- INTRODUÇÃO O termo probabilidade é usado de modo muito amplo na conversação diária para sugerir um certo grau de incerteza sobre o que ocorreu no passado, o que ocorrerá no futuro ou o que está ocorrendo
1 1- INTRODUÇÃO O termo probabilidade é usado de modo muito amplo na conversação diária para sugerir um certo grau de incerteza sobre o que ocorreu no passado, o que ocorrerá no futuro ou o que está ocorrendo
Avaliação de Empresas Profa. Patricia Maria Bortolon
 Avaliação de Empresas RISCO E RETORNO Aula 2 Retorno Total É a variação total da riqueza proporcionada por um ativo ao seu detentor. Fonte: Notas de Aula do Prof. Claudio Cunha Retorno Total Exemplo 1
Avaliação de Empresas RISCO E RETORNO Aula 2 Retorno Total É a variação total da riqueza proporcionada por um ativo ao seu detentor. Fonte: Notas de Aula do Prof. Claudio Cunha Retorno Total Exemplo 1
Teste de Avaliação Escrita
 Teste de Avaliação Escrita Duração: 9 minutos 8 de outubro de Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo /4 Matemática 9.º B Nome: N.º Classificação: Fraco (% 9%) Insuficiente (% 49%) Suficiente
Teste de Avaliação Escrita Duração: 9 minutos 8 de outubro de Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo /4 Matemática 9.º B Nome: N.º Classificação: Fraco (% 9%) Insuficiente (% 49%) Suficiente
