Sistemas Lineares. Prof. Alexandre Trofino
|
|
|
- Luiz Fernando Tuschinski Brezinski
- 8 Há anos
- Visualizações:
Transcrição
1 Sistemas Lineares Prof. Alexandre Trofino Departamento de Automação e Sistemas Centro Tecnológico Universidade Federal de Santa Catarina cep 884-9, Florianópolis-SC trofino@lcmi.ufsc.br Internet: trofino Esta apostila bem como as experiências de laboratório no site são de responsabilidade do professor Alexandre Trofino. Este material pode ser livremente utilizado para fins didáticos, respeitando-se os direitos autorais. Fica proibido o uso para fins comerciais. Todos os resultados de cálculos e simulações foram obtidos com o pacote scilab que é distribuído gratuitamente no site
2 2
3 Conteúdo Introdução Geral 5. Termos usuais em controle Sistemas de Malha Aberta Sistemas de Malha Fechada Sinais de Tempo Contínuo e Discreto Definição de Sistemas Lineares Transformada de Laplace 9 2. Introdução e Noções de Funções Complexas Definição e Região de Convergência Propriedades Operação Linear Função Transladada em Atraso Funções Porta-deslocada e Impulso Multiplicação de f(t) por e αt Mudança na Escala de Tempo Teorema da Diferenciação Real Teorema do Valor Final Teorema do Valor Inicial Teorema da Integração Real Teorema da Diferenciação Complexa
4 Conteúdo Integral de Convolução Transformada Inversa Frações parciais para pólos distintos Frações Parciais para pólos repetidos Frações Parciais para casos especiais Sinais com energia limitada Resolução de Equações Diferenciais Respostas de Estado Zero e Entrada Zero Função de Transferência e Estabilidade Diagrama de Blocos Sistemas Realimentados Estabilidade de Conexões Sistemas Realimentados em presença de distúrbios Problemas complementares Resposta ao Degrau Introdução Análise de Sistemas de Primeira Ordem Análise de Sistemas de Segunda Ordem Caso sem amortecimento (ξ = ) Caso Subamortecido ( < ξ < ) Caso Superamortecido (ξ ) Caso instável (ξ < ) Índices de desempenho Servomecanismo para controle de posição Problemas complementares Resposta em frequência 77
5 Conteúdo Resposta Senoidal em Regime Permanente Gráficos Logarítmicos Construção do Diagrama de Bode Sistemas de Fase Mínima e Não-Mínima Gráficos de Nyquist (ou polares) Problemas Complementares Sinais e a Transformada de Fourier 5. Conexões entre Fourier e Laplace Energia de sinais Cálculo de algumas transformadas Sinal Exponencial Unilateral (t ) Sinal Porta Sinal Impulso: Funções Constante, Sinal e Degrau Sinais Senoidais Exponencial Eterna e jω t Funções Periódicas Propriedades da transformada Linearidade Simetria Escalonamento Deslocamento em Frequência e Modulação Deslocamento no Tempo Diferenciação e Integração no Tempo Diferenciação em Frequência Convolução
6 Conteúdo Amostragem Problemas complementares Sistemas Discretos e Amostrados Introdução Conversão A/D Conversão D/A e Sample-and-Hold Sinais e Sistemas de Tempo Discreto Transformada Z Definição e exemplos Relação com a transformada de Laplace Propriedades da Transformada Z Linearidade Teorema do Valor Inicial Teorema do Valor Final Obtenção de F (z) a partir de F (s) Convolução Discreta Transformada Z Inversa Método da divisão polinomial Método das frações parciais de X(z)/z Solução de Equações recursivas Função de Transferência Discreta e Estabilidade Respostas de Estado Zero e Entrada Zero Resposta ao Pulso e Estabilidade Sistemas Amostrados Sistemas Realimentados Escolha do Período de Amostragem
7 Conteúdo Resposta em Frequência Problemas Complementares
8 Conteúdo 8
9 Lista de Figuras. Sistema de malha aberta Sistema de controle de malha fechada Sistema realimentado de controle por computador Servomotor para posicionamento de uma antena Variável de tempo contínuo (sinal analógico) Variável de tempo discreto (sequência) Circuito RLC série Transformada direta e inversa de Laplace Representação gráfica de uma função complexa Relação entre f(t) e sua transformada de Laplace Função deslocada em atraso Função Porta de área unitária Derivada de funções descontínuas Função dente de serra e sua derivada Função onda quadrada Relação entre f(t) e sua transformada F (s) Diagrama de simulação analógica Respostas x(t) do diagrama de simulação analógica Respostas de Estado Zero e Entrada Zero Circuito RLC série
10 Lista de Figuras Diagrama entrada/saída de um circuito Diagrama de blocos simplificado Diagrama de blocos detalhado Sistema realimentado Sistema realimentado simplificado Diagrama de blocos de um circuito RLC-série Conexão de dois sistemas em paralelo Conexão de dois sistemas em realimentação Sistema realimentado perturbado Diagrama para referência nula Diagrama para distúrbio nulo Sistema para controle de posição Curvas típicas da resposta ao degrau Diagrama de bloco entrada/saída Circuito RC Sistema de primeira ordem padrão Resposta ao degrau de um sistema de primeira ordem padrão Sistema de segunda ordem padrão Índices de desempenho para resposta ao degrau Resposta ao degrau do sistema Diagrama funcional do sistema de posicionamento Diagrama de blocos do comparador e potenciômetro Diagrama de blocos com adição do amplificador Motor DC controlado pela armadura (rotor) Diagrama de blocos com adição do motor DC Diagrama de blocos com adição da engrenagem
11 Lista de Figuras Sistema mecânico da plataforma e antena Diagrama completo do sistema de posicionamento Diagrama simplificado de posicionamento da antena Diagrama de posicionamento na forma padrão Resposta ao degrau do sistema de controle Diagrama funcional para realimentação de velocidade Sistema de controle com realimentação de velocidade Resposta ao degrau do sistema de controle Sistema com realimentação de velocidade e posição Sistema de controle de velocidade Resposta ao degrau unitário Resposta temporal para sen(ω t) com ω = {, 2; 2; 2; } rd/s Resposta de regime ao seno Resposta de regime ao cosseno Circuito RC Resposta em frequência (Bode) do circuito RC Circuito RLC Resposta em frequência (Bode) do circuito RLC Resposta em frequência (Nyquist) do circuito RLC Resposta em frequência (Black) do circuito RLC Resposta em frequência com G(s) instável Diagrama de Bode dos termos 2 e s Diagrama de Bode do termo 4s Diagrama de Bode de G(s) = 2 s(4s) Diagrama de Bode dos termos s e s Diagrama de Bode do termo T s e assíntotas
12 Lista de Figuras Diagrama de Bode do termo ω 2 n s 2 2ξω n sω 2 n e assíntotas Diagrama de Bode do termo G (s) =.(.s) s e assíntotas Diagrama de Bode do termo G 2 (s) = G (s) s 4.9 Diagrama de Bode do termo G(s) = G 2 (s) 4 s 2 2 s e assíntotas e assíntotas Circuito de fase não mínima (r 2 > r ) Caso (a): Sistema de fase não mínima (r 2 > r ) Caso (b): Sistema de fase mínima (r 2 < r ) Diagrama de Nyquist de G (2πf), G 2 (2πf), G 3 (2πf), G 4 (2πf) Diagrama de Nyquist de H (2πf), H 2 (2πf), H 3 (2πf), H 4 (2πf) Diagrama de Bode de um sistema linear invariante Resposta em frequência de um sistema linear invariante Operador Transformada de Fourier e seu inverso Sinal Porta de largura τ Função Sa(x) = sen(x) x Função Sinal Função onda quadrada de período 2π Aproximação de sinais pela série trigonométrica de Fourier Trem de impulsos e sua transformada Transformada de Fourier do sinal porta de largura unitária G (t) Transformada de Fourier do sinal cos(t)g (t) Demodulação de um sinal Sinal linear por trechos Derivada do sinal linear por trechos Derivada segunda do sinal linear por trechos Filtro de primeira ordem com F (s) = s Transmissão e recuperação de sinais
13 Lista de Figuras Espectro do sinal antes e após amostragem: Caso ω a > 2 ω Filtro ideal para recuperação do sinal: Caso ω a > 2 ω Espectro do sinal antes e após amostragem: Caso ω a < 2 ω Espectro do sinal f(t) = cos(πt) sen(πt) Sistema de amostragem e recuperação de sinais Espectro dos sinais x(t), r(t) Espectro do sinal amostrado Sistema com modulação e discretização Representação de um sinal de tensão analógico não negativo em código binário de 4 bits Esquema simplificado de um circuito sample-and-hold e seu diagrama de blocos (a) Diagrama de blocos de um conversor A/D com sample-and-hold e (b) funcionamento do sistema (a) Conversor D/A com S/H e (b) Sinais de entrada e saída Amostrador ideal: produto por um trem de impulsos Segurador de ordem zero: a saída é constante por trechos Sample-and-Hold visto como um amostrador ideal em cascata com um segurador de ordem zero Circuito RC: resposta livre Valor da corrente no capacitor nos instantes t = kt Circuito RC com entrada constante por trechos Representação de um sistema discreto Sistema controlado por computador Região de convergência das transformadas do degrau unitário Relação biunívoca entre a sequência x(kt ) e sua transformada Z Relação entre localização pólos e evolução temporal Relação entre localização pólos e evolução temporal
14 Lista de Figuras Relação entre localização pólos e evolução temporal Obtenção de F (z) a partir de F (s) Sequências convergentes e a localização dos pólos no plano z Sistema discreto genérico Sistema amostrado e seu discreto equivalente Resumo dos resultados de conversão de Laplace para Z Sistema amostrado com conversor D/A e S/H Circuito com entrada constante por trechos (a) Dois sistemas amostrados em cascata; (b) Dois sistemas contínuos em cascata Sistema de controle digital e seu modelo discreto Sistema de controle digital com medidor analógico (a) e digital (b) Controle digital de posição angular através de um motor DC Sistema discreto estável Resposta frequencial de um sistema discreto Circuito RLC com entrada constante por trechos Sistema de controle de velocidade Caracterização entrada/saída dos sistemas Entrada: tensão x(t) ; saída: tensão v(t) ; R= Ω, C= F Sistema de controle
15 Capítulo Introdução Geral. Termos usuais em controle Planta Equipamento (ou parte dele) destinado à realizar uma dada operação. (Objeto físico a ser controlado: caldeira, motor, reator químico,...). Processo Fenômenos (naturais ou criados artificialmente) que evoluem progressivamente segundo dinâmicas que lhe são próprias. (Fenômeno a ser controlado: processos químicos, econômicos, biológicos,...). Sistema Equipamento ou fenômeno físico. Distúrbio Sinal indesejado (interno ou externo). Controle Realimentado Operação que visa corrigir (automaticamente ou manualmente) certas variáveis (grandezas físicas) de um sistema. Diminui o efeito de fenômenos indesejáveis. Servomecanismo É um sistema de controle realimentado para controle automático de posição, velocidade ou aceleração. Muito frequente na indústria. Sistemas Reguladores Automáticos Sistema de controle cujo principal objetivo é manter constante algumas variáveis do mesmo. (Controle de nível constante, posição constante, velocidade, aceleração,...). Exemplos: robos, elevadores, estufas,....2 Sistemas de Malha Aberta Sistemas onde a variável a ser controlada (saída) não interfere na ação de controle (variável de entrada) são conhecidos como Sistemas de malha aberta. A saída é sensível à fenômenos indesejáveis sobre o processo (perturbações, variações nos parâmetros,...). Possui pouca performance na prática quando existem perturbações. No entanto possui custo menor em geral.
16 .3. Sistemas de Malha Fechada 6 Perturbações Entrada SISTEMA Saída Figura.: Sistema de malha aberta.3 Sistemas de Malha Fechada Sistemas onde a variável de controle (Entrada) depende (Direta ou indiretamente) da variável a ser controlada (Saída) recebem o nome de sistemas de malha fechada. Nesse caso possíveis distorções na variável controlada provocadas por distúrbios no sistema são automaticamente (on line) corrigidas. perturbação Ref. Comparador Controlador Atuador SISTEMA Variável Observada sinal de medição Medidor ruído de medição Figura.2: Sistema de controle de malha fechada Controlador Ref. Comparador A/D Computador D/A Atuador SISTEMA Saída Medidor Figura.3: Sistema realimentado de controle por computador Exemplo. Considere o servomecanismo para controle de posição da antena indicado na Figura.4. Comparando com o diagrama da figura.2 podemos identificar os seguintes elementos: Sistema: Antena plataforma engrenagens Perturbações: Grandezas externas que atuam de forma indesejada no sistema. exemplo, ventos que provocam torques de perturbação na posição da antena. Por Variável observada: Posição angular da antena
17 .4. Sinais de Tempo Contínuo e Discreto 7 potenciômetro referência r(t) V r (t) erro amplificador de potência comparador V c(t) e(t) E a (t) posição da antena c(t) potenciômetro engrenagem motor DC Figura.4: Servomotor para posicionamento de uma antena Variável medida: Sinal de medição gerado pelo potenciômetro. Note que a variável medida pode ser diferente da variável observada quando existem ruídos de medição. Medidor: Potenciômetro Referência: Valor desejado da grandeza observada Comparador: somador de tensões Controlador: Nesse exemplo o controlador é um elemento unitário entre o comparador e o amplificador. Em geral, o controlador é um filtro que manipula o sinal de erro antes do amplificador de potência. Em sistemas mais complexos o controlador pode ser um algorítimo implementado num computador. Atuador: Amplificador de Potência motor.4 Sinais de Tempo Contínuo e Discreto TEMPO CONTÍNUO: t é uma variável contínua. Nesse caso um sinal f(t) será um sinal analógico, isto é, um sinal de tempo contínuo. f(t) Ref. t Figura.5: Variável de tempo contínuo (sinal analógico) TEMPO DISCRETO: t é uma variável discreta que assume valores apenas em instantes discretos do tempo. Por exemplo, t = kt onde k é uma variável k =,, 2,... e T é uma constante. Nesse caso um sinal f(kt ) será uma sequência, isto é, um sinal de tempo discreto.
18 .5. Definição de Sistemas Lineares 8 Ref. f(kt) t = kt Figura.6: Variável de tempo discreto (sequência).5 Definição de Sistemas Lineares SISTEMAS LINEARES: São fenômenos ou dispositivos cujo comportamento dinâmico pode ser descrito por equações diferenciais (ou recursivas) lineares. SISTEMAS LINEARES INVARIANTES NO TEMPO: São sistemas lineares descritos por equações diferenciais (ou recursivas) com coeficientes constantes.
19 Capítulo 2 Transformada de Laplace 2. Introdução e Noções de Funções Complexas O comportamento da maioria dos sistemas físicos pode ser representado através de equações diferenciais. Neste curso vamos nos restringir à sistemas que podem ser representados por equações diferenciais ordinárias, lineares, à parâmetros invariantes no tempo. R L V(t) C V c(t) - Figura 2.: Circuito RLC série - Exemplo 2. Condidere o circuito da figura 2.. A relação de causa-efeito da tensão v(t) (Entrada) sobre a tensão v C (t) (Saída) no capacitor é um sistema descrito pela equação diferencial seguinte: v(t) = RC v C (t) LC v C (t) v C (t), Equação diferencial ordinária linear Parâmetros invariantes no tempo dv(t) dt = v(t) Sistemas mais complicados são muitas vezes modelados por equações diferenciais não lineares e muito frequentemente os parâmetros variam com o tempo. No entanto, o comportamento desses sistemas pode ser aproximado por equações diferenciais lineares invariantes no tempo, nas vizinhanças de um ponto de operação. As técnicas para a
20 2.. Introdução e Noções de Funções Complexas 2 obtenção desses modelos lineares invariantes no tempo consistem em expandir os termos não lineares pela Série de Taylor e aproximá-los pela parte linear da série. Por exemplo, para a função y(t) = sen(t) obteríamos uma aproximação linear nas vizinhanças da origem que é dada por y lin (t) = t e é fácil de verificar que a função y(t) = sen(t) se comporta aproximadamente como y lin (t) = t para pequenos valores da variável t. A Transformada de Laplace é uma técnica extremamente útil na solução de equações diferenciais lineares invariantes no tempo. É através da Transformada de Laplace que se obtém a noção de Função de Transferência de um sistema. A Transformada de Laplace transforma um função da variável tempo, digamos f(t), numa outra função F (s) onde s = σ jω é uma variável complexa. Em determinadas condições, as funções f(t) e sua transformada F (s) estão relacionadas de forma bi-unívoca: Transf. Direta f(t) LAPLACE F(s) Transf. Inversa Figura 2.2: Transformada direta e inversa de Laplace PROPRIEDADES DE FUNÇÕES COMPLEXAS: Neste curso vamos nos restringir, com poucas excessões, à funções complexas racionais. Definição 2. (Função Racional) Uma função G(s) da variável complexa s = σjω é racional se G(s) pode ser expressa como a divisão de dois polinômios da variável complexa s. A figura abaixo ilustra uma função complexa G(s) em termos de suas coordenadas retangular e polar. onde G(s) = G 2 x G 2 y e G(s) = tan G y /G x. Im[G(s)] G y G(s) = G x jg y = G(s) e j G(s) G x Re[G(s)] Figura 2.3: Representação gráfica de uma função complexa Complexo conjugado: A conjugação complexa é uma operação que consiste em trocar o sinal da parte imaginária, se o número estiver representado nas coordenadas retangulares, ou de forma equivalente, trocar o sinal da fase, se o número estiver representado
21 2.. Introdução e Noções de Funções Complexas 2 nas coordenadas polares. Representaremos o complexo conjugado do número complexo G(s), indicado na figura 2.3, por G(s) = G x jg y = G(s) e j G(s). Duas propriedades importantes da conjugação complexa são indicadas a seguir. A, B são dois números complexos então AB = A B e A B = A B. Se Definição 2.2 (Pólos e Zeros) Seja G(s) = N(s) onde N(s) e D(s) são dois polinômios D(s) com coeficientes reais. Define-se pólos e zeros de G(s) como sendo os valores de s tais que: - Zeros de G(s): s tal que N(s) = - Pólos de G(s): s tal que D(s) = Exemplo 2.2 A transformada de Laplace da função g(t) =, 5, 5e 2t, função complexa G(s) = s que possui os seguintes pólos e zeros: s(s 2) t é a - Zeros de G(s): s = - Pólos de G(s): s =, s = 2 Note que cada pólo da função G(s) está associado à uma exponencial da função g(t). Na realidade os pólos são os expoentes das exponenciais. O número complexo: e jθ = cosθ jsenθ possui módulo unitário e fase θ, como indicado a seguir. e jθ = cos 2 θ sen 2 θ = e jθ senθ = tan cosθ = θ Definição 2.3 (Função Analítica) Uma função G(s) é analítica numa região se G(s) e todas as suas derivadas existem nessa região. Exemplo 2.3 A função G(s) = s é analítica fora do ponto s = (Pólo de G(s)). As operações de derivada e integral envolvendo funções complexas analíticas se fazem de maneira habitual, isto é, as regras usuais de derivada e integral se aplicam diretamente.
22 2.2. Definição e Região de Convergência Definição e Região de Convergência Para uma função f(t) com t, define-se Transformada de Laplace de f(t) como sendo a função complexa F (s) obtida através da integral: F (s) = L[f(t)] = f(t)e st dt (2.) onde s = σ jω é a variável complexa introduzida pela transformada. Sob certas condições (que veremos a seguir) podemos também definir a Transformada Inversa de Laplace da seguinte forma: f(t) = L [F (s)] = 2πj cj c j F (s)e st ds (2.2) onde t e c é um número real associado à região do plano s = σ jω onde a função F (s) está definida. Esta região é chamada região de convergência da Transformada de Laplace. Dentro dessa região as funções f(t) para t e F (s) estão ligadas de maneira biunívoca, como ilustra a figura a seguir. Trans. Direta f(t) t F (s) Re[s] > c Tranf. Inversa Figura 2.4: Relação entre f(t) e sua transformada de Laplace Exemplo 2.4 Seja f(t) = e 2t, para t. F (s) = L[f(t)] = Note que s = σ jω e Assim, e 2t e st dt = s 2 e (s 2)t = s 2 [ lim t e (s 2)t lim t e (s 2)t ] = s 2 s 2 lim t e (s 2)t lim t e (s 2)t = e jωt = cosωt jsenωt =. ± para Re[s] = σ < 2 indefinido para Re[s] = σ = 2 para Re[s] = σ > 2.
23 2.2. Definição e Região de Convergência 23 Logo, a Transformada de Laplace da função e 2t, t só está definida na região do plano complexo definida por Re[s] > 2 e nessa região obtemos: F (s) = L[e 2t ] = s 2 A região do plano complexo onde a Integral de Laplace está definida e é finita recebe o nome de região de convergência da Transformada de Laplace. Mostra-se que ao escolhermos um contorno para a integral: 2πj cj c j F (s)e st ds de tal forma que c > 2 (contorno dentro da região de convergência) então o resultado da integral acima é e 2t para t. Existem funções, como por exemplo e t2, t, para as quais a Transformada de Laplace não existe, isto é, não existe região de convergência da Integral de Laplace. No entanto, todos os sinais de interesse prático são transformáveis por Laplace. A região de convergência da Transformada de Laplace é um formalismo matemático que normalmente é omitido no cálculo da transformada. No entanto é importante lembrar que qualquer que seja a região de convergência, as funções f(t) para t e F (s) para Re[s] > c estão relacionados de maneira biunívoca. Os casos em que f(t) para t < são de interesse marginal no cálculo da Transformada de Laplace e não serão considerados nesse curso. Uma vez obtida a transformada de Laplace F (s) podemos deduzir sua região de convergência. Ela é dada pela região do plano complexo à direita do pólo mais à direita da função F (s). Exemplo 2.5 (Exponencial real) f(t) = e at, t F (s) = L[e at ] = e at e st dt = s a e (s a)t = s a Exemplo 2.6 (Degrau Unitário) Função Degrau Unitário u(t) = L[u(t)] = (Região de Convergência Re[s] > ) e st dt = s e st = s. {, t <, t {, t < Exemplo 2.7 (Rampa) Função Rampa f(t) = At, t, A constante L[f(t)] = A ( udv = uv vdu) te st dt = At e st s Ae st s dt = A s e st dt = A s 2.
24 2.3. Propriedades 24 {, t < Exemplo 2.8 (Senóide) Função Senoidal f(t) = sen(ω t), t, ω cte L[f(t)] = sen(ω t)e st dt = = [ ] 2j s jω s jω e jωt e jω t e st dt 2j = ω s 2 ω 2 RESUMO u(t) : Pólo simples na origem. Função Constante no tempo. s tu(t) s 2 : Pólo duplo na origem. Função cresce linearmente no tempo. e αt u(t) : Pólo em s = α. Cresce exponencialmente no tempo se pólo for positivo sα (α < ). Decresce exponecialmente no tempo se pólo for negativo (α > ). Valor constante no tempo se o pólo for na origem. sen(ω t)u(t) ω : Pólos complexos conjugados sobre o eixo imaginário (s = ±jω s 2 ω 2 ). Função oscila no tempo sem amortecimento. 2.3 Propriedades A Transformada de Laplace possui várias propriedades que, em geral, simplificam o cálculo da transformada se comparado com a aplicação direta da definição (2.). Todas as propriedades apresentadas nessa seção estão provadas em []. Por conveniência repetiremos algumas das provas a título de exercício Operação Linear Sejam f (t) e f 2 (t) duas funções e α e α 2 duas constantes. Então: L[α f (t) α 2 f 2 (t)] = α L[f (t)] α 2 L[f 2 (t)] Prova: Utilizando a definição (2.) temos: L[α f (t) α 2 f 2 (t)] = (α f (t) α 2 f 2 (t))e st dt = α f (t)e st dt α 2 f 2 (t)e st dt = α L[f (t)] α 2 L[f 2 (t)]
25 2.3. Propriedades Função Transladada em Atraso Seja f(t) uma função, u(t) o degrau unitário e α uma constante. Então: L[f(t α)u(t α)] = e αs L[f(t)] f(t) f(t α)u(t α) t α t Figura 2.5: Função deslocada em atraso Prova: Aplicando a definição temos: L[f(t α)u(t α)] = f(t α)u(t α)e st dt Definindo τ = t α podemos rescrever a integral acima como L[f(t α)u(t α)] = α f(τ)u(τ)e s(τα) dτ = e sα f(τ)u(τ)e sτ dτ como f(τ)u(τ) = para α τ < temos: = e sα f(τ)u(τ)e sτ dτ α = e sα f(τ)e sτ dτ = e sα L[f(t)] Funções Porta-deslocada e Impulso As funções Porta-deslocada e Impulso possuem propriedades importantes no contexto da Transformada de Laplace. Função Porta-deslocada: Usaremos a notação f p (t) para representar a função portadeslocada de área unitária. { f p (t) = t, < t < t, > t > t sendo t O uma constante
5 Transformadas de Laplace
 5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial. Transformada de Laplace
 Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio do Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Transformada de Laplace. Parte 3
 Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
² Servomecanismo: Sistema de controle realimentado para controle automático de posição, velocidade ou aceleração. Muito empregado na indústria.
 1. Introdução 1.1. De nições Básicas ² Sistema: Interconexão de dispositivos e elementos para cumprir um objetivo desejado. ² Processo: Um sistema ou dispositivo a ser controlado. ² Sistema de controle:
1. Introdução 1.1. De nições Básicas ² Sistema: Interconexão de dispositivos e elementos para cumprir um objetivo desejado. ² Processo: Um sistema ou dispositivo a ser controlado. ² Sistema de controle:
11/07/2012. Professor Leonardo Gonsioroski FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA.
 FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
EXERCÍCIOS RESOLVIDOS
 ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace
 Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Resposta Transitória de Circuitos com Elementos Armazenadores de Energia
 ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
Caracterização temporal de circuitos: análise de transientes e regime permanente. Condições iniciais e finais e resolução de exercícios.
 Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Estabilidade. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
ANÁLISE LINEAR DE SISTEMAS
 ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
Universidade Federal do Rio de Janeiro. Princípios de Instrumentação Biomédica. Módulo 4
 Universidade Federal do Rio de Janeiro Princípios de Instrumentação Biomédica Módulo 4 Faraday Lenz Henry Weber Maxwell Oersted Conteúdo 4 - Capacitores e Indutores...1 4.1 - Capacitores...1 4.2 - Capacitor
Universidade Federal do Rio de Janeiro Princípios de Instrumentação Biomédica Módulo 4 Faraday Lenz Henry Weber Maxwell Oersted Conteúdo 4 - Capacitores e Indutores...1 4.1 - Capacitores...1 4.2 - Capacitor
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
Circuitos Elétricos III
 Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 2 Equivalente
Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 2 Equivalente
INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES
 1 INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES 1.1 - Instrumentação Importância Medições experimentais ou de laboratório. Medições em produtos comerciais com outra finalidade principal. 1.2 - Transdutores
1 INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES 1.1 - Instrumentação Importância Medições experimentais ou de laboratório. Medições em produtos comerciais com outra finalidade principal. 1.2 - Transdutores
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS
 REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92)
 ADL22 4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92) A transformada de Laplace fornece: (4.93) (4.94) A fim de separar X(s), substitua sx(s)
ADL22 4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92) A transformada de Laplace fornece: (4.93) (4.94) A fim de separar X(s), substitua sx(s)
Transformada z. ADL 25 Cap 13. A Transformada z Inversa
 ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação
 Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
Análise de Circuitos Elétricos III
 Análise de Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais Introdução à Transformada de Laplace A Transformada
Análise de Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais Introdução à Transformada de Laplace A Transformada
Análise e Processamento de Bio-Sinais. Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas. Licenciatura em Engenharia Física
 Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Transformada de Laplace
 Capítulo 8 Transformada de Laplace A transformada de Laplace permitirá que obtenhamos a solução de uma equação diferencial ordinária de coeficientes constantes através da resolução de uma equação algébrica.
Capítulo 8 Transformada de Laplace A transformada de Laplace permitirá que obtenhamos a solução de uma equação diferencial ordinária de coeficientes constantes através da resolução de uma equação algébrica.
Modelagem de Sistemas Dinâmicos. Eduardo Camponogara
 Equações Diferenciais Ordinárias Modelagem de Sistemas Dinâmicos Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle
Equações Diferenciais Ordinárias Modelagem de Sistemas Dinâmicos Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle
SISTEMAS DE CONTROLE II
 SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
PARTE 2 FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL
 PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
9. Derivadas de ordem superior
 9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 3
 Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Sistemas de Controle Digital
 ADL 24 Cap 13 Sistemas de Controle Digital Vantagens dos Computadores Digitais O uso de computadores digitais na malha leva às seguintes vantagens sobre os sistemas analógicos: (1) custo, (2) flexibilidade
ADL 24 Cap 13 Sistemas de Controle Digital Vantagens dos Computadores Digitais O uso de computadores digitais na malha leva às seguintes vantagens sobre os sistemas analógicos: (1) custo, (2) flexibilidade
Tutorial de Eletrônica Aplicações com 555 v2010.05
 Tutorial de Eletrônica Aplicações com 555 v2010.05 Linha de Equipamentos MEC Desenvolvidos por: Maxwell Bohr Instrumentação Eletrônica Ltda. Rua Porto Alegre, 212 Londrina PR Brasil http://www.maxwellbohr.com.br
Tutorial de Eletrônica Aplicações com 555 v2010.05 Linha de Equipamentos MEC Desenvolvidos por: Maxwell Bohr Instrumentação Eletrônica Ltda. Rua Porto Alegre, 212 Londrina PR Brasil http://www.maxwellbohr.com.br
AULA #12. Estabilidade de Sistemas de Controle por
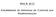 AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
2 A Derivada. 2.1 Velocidade Média e Velocidade Instantânea
 2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
Período : exp( j α) α/2π = N/K (irredutível) em que se N,K Z então K é o período.
 Período : exp( j α) α/2π = N/K (irredutível) em que se N,K Z então K é o período. sin(t) = sin (t + T), ou exp(t) = exp(t+t) em que T é o período. [sin(a) e/ou cos(a) ]+[ sin(b) e/ou cos(b)] = o periodo
Período : exp( j α) α/2π = N/K (irredutível) em que se N,K Z então K é o período. sin(t) = sin (t + T), ou exp(t) = exp(t+t) em que T é o período. [sin(a) e/ou cos(a) ]+[ sin(b) e/ou cos(b)] = o periodo
x0 = 1 x n = 3x n 1 x k x k 1 Quantas são as sequências com n letras, cada uma igual a a, b ou c, de modo que não há duas letras a seguidas?
 Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Desempenho de Sistemas de Controle Realimentados
 Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
Aula 3 OS TRANSITÒRIOS DAS REDES ELÉTRICAS
 Aula 3 OS TRANSITÒRIOS DAS REDES ELÉTRICAS Prof. José Roberto Marques (direitos reservados) A ENERGIA DAS REDES ELÉTRICAS A transformação da energia de um sistema de uma forma para outra, dificilmente
Aula 3 OS TRANSITÒRIOS DAS REDES ELÉTRICAS Prof. José Roberto Marques (direitos reservados) A ENERGIA DAS REDES ELÉTRICAS A transformação da energia de um sistema de uma forma para outra, dificilmente
2.3- DIAGRAMAS DE BLOCOS E DE FLUXO DE SINAL. FÓRMULA DE MASON DIAGRAMA DE BLOCOS DB
 2.3 DIRMS DE BLOOS E DE FLUXO DE SINL. FÓRMUL DE MSON DIRM DE BLOOS DB Os sistemas de controle, geralmente, são constituídos por vários componentes ou partes interligadas. Para mostrar estas interconexões
2.3 DIRMS DE BLOOS E DE FLUXO DE SINL. FÓRMUL DE MSON DIRM DE BLOOS DB Os sistemas de controle, geralmente, são constituídos por vários componentes ou partes interligadas. Para mostrar estas interconexões
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aula 2 Ref. Butkov, cap. 8, seção 8.2
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 2 Ref. Butkov, cap. 8, seção 8.2 O Método de Separação de Variáveis A ideia central desse método é supor que a solução
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 2 Ref. Butkov, cap. 8, seção 8.2 O Método de Separação de Variáveis A ideia central desse método é supor que a solução
Técnico em Eletrotécnica
 Técnico em Eletrotécnica Caderno de Questões Prova Objetiva 2015 01 Em uma corrente elétrica, o deslocamento dos elétrons para produzir a corrente se deve ao seguinte fator: a) fluxo dos elétrons b) forças
Técnico em Eletrotécnica Caderno de Questões Prova Objetiva 2015 01 Em uma corrente elétrica, o deslocamento dos elétrons para produzir a corrente se deve ao seguinte fator: a) fluxo dos elétrons b) forças
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 1
 597 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Movimentos Periódicos Para estudar movimentos oscilatórios periódicos é conveniente ter algum modelo físico em mente. Por exemplo, um
597 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Movimentos Periódicos Para estudar movimentos oscilatórios periódicos é conveniente ter algum modelo físico em mente. Por exemplo, um
Eletrônica Industrial Apostila sobre Modulação PWM página 1 de 6 INTRODUÇÃO
 Eletrônica Industrial Apostila sobre Modulação PWM página 1 de 6 Curso Técnico em Eletrônica Eletrônica Industrial Apostila sobre Modulação PWM Prof. Ariovaldo Ghirardello INTRODUÇÃO Os controles de potência,
Eletrônica Industrial Apostila sobre Modulação PWM página 1 de 6 Curso Técnico em Eletrônica Eletrônica Industrial Apostila sobre Modulação PWM Prof. Ariovaldo Ghirardello INTRODUÇÃO Os controles de potência,
Circuitos Osciladores
 Circuitos Osciladores Em virtude da realimentação do sinal, a estabilidade do circuito deve ser analisada pois quando a freqüência aumenta, o deslocamento de fase varia e como parte deste sinal é adicionado
Circuitos Osciladores Em virtude da realimentação do sinal, a estabilidade do circuito deve ser analisada pois quando a freqüência aumenta, o deslocamento de fase varia e como parte deste sinal é adicionado
Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros
 Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
RECEPTOR AM DSB. Transmissor. Circuito Receptor AM DSB - Profº Vitorino 1
 RECEPTOR AM DSB Transmissor Circuito Receptor AM DSB - Profº Vitorino 1 O receptor super-heteródino O circuito demodulador que vimos anteriormente é apenas parte de um circuito mais sofisticado capaz de
RECEPTOR AM DSB Transmissor Circuito Receptor AM DSB - Profº Vitorino 1 O receptor super-heteródino O circuito demodulador que vimos anteriormente é apenas parte de um circuito mais sofisticado capaz de
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE
 INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
Fundamentos de Telecomunicações
 Fundamentos de Telecomunicações Translação de Frequências A utilização eficaz de um canal de transmissão pode requerer por vezes a utilização de uma banda de frequências diferente da frequência original
Fundamentos de Telecomunicações Translação de Frequências A utilização eficaz de um canal de transmissão pode requerer por vezes a utilização de uma banda de frequências diferente da frequência original
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS
 ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS 01 - Questão Esta questão deve ser corrigida? SIM NÃO Um transformador de isolação monofásico, com relação de espiras N
ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS 01 - Questão Esta questão deve ser corrigida? SIM NÃO Um transformador de isolação monofásico, com relação de espiras N
Universidade Federal do Rio de Janeiro. Circuitos Elétricos I EEL420. Módulo 2
 Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL420 Módulo 2 Thévenin Norton Helmholtz Mayer Ohm Galvani Conteúdo 2 Elementos básicos de circuito e suas associações...1 2.1 Resistores lineares
Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL420 Módulo 2 Thévenin Norton Helmholtz Mayer Ohm Galvani Conteúdo 2 Elementos básicos de circuito e suas associações...1 2.1 Resistores lineares
Filtros de sinais. Conhecendo os filtros de sinais.
 Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Processos em Engenharia: Introdução a Servomecanismos
 Processos em Engenharia: Introdução a Servomecanismos Prof. Daniel Coutinho coutinho@das.ufsc.br Departamento de Automação e Sistemas DAS Universidade Federal de Santa Catarina UFSC DAS 5101 - Aula 7 p.1/47
Processos em Engenharia: Introdução a Servomecanismos Prof. Daniel Coutinho coutinho@das.ufsc.br Departamento de Automação e Sistemas DAS Universidade Federal de Santa Catarina UFSC DAS 5101 - Aula 7 p.1/47
CIRCUITOS ELÉTRICOS RESOLUÇÃO DE CIRCUITOS TRANSITÓRIOS NO DOMÍNIO DA FREQÜÊNCIA
 1 CIRCUITOS ELÉTRICOS RESOLUÇÃO DE CIRCUITOS TRANSITÓRIOS NO DOMÍNIO DA FREQÜÊNCIA Simulação de chaves utilizando a função degrau a) Fonte de tensão que entra em operação em t = 0 Substituindo a chave
1 CIRCUITOS ELÉTRICOS RESOLUÇÃO DE CIRCUITOS TRANSITÓRIOS NO DOMÍNIO DA FREQÜÊNCIA Simulação de chaves utilizando a função degrau a) Fonte de tensão que entra em operação em t = 0 Substituindo a chave
Somatórias e produtórias
 Capítulo 8 Somatórias e produtórias 8. Introdução Muitas quantidades importantes em matemática são definidas como a soma de uma quantidade variável de parcelas também variáveis, por exemplo a soma + +
Capítulo 8 Somatórias e produtórias 8. Introdução Muitas quantidades importantes em matemática são definidas como a soma de uma quantidade variável de parcelas também variáveis, por exemplo a soma + +
Laboratório de Conversão Eletromecânica de Energia B
 Laboratório de Conversão Eletromecânica de Energia B Prof a. Katia C. de Almeida 1 Obtenção Experimental dos Parâmetros do Circuito Equivalente do Motor de Indução Monofásico 1.1 Introdução 1.1.1 Motores
Laboratório de Conversão Eletromecânica de Energia B Prof a. Katia C. de Almeida 1 Obtenção Experimental dos Parâmetros do Circuito Equivalente do Motor de Indução Monofásico 1.1 Introdução 1.1.1 Motores
Amostrador PAM A/D PCM D/A PAM Filtro. Figura 1 Digrama de Blocos PCM
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA ELÉTRICA SISTEMAS DE TELECOMUNICAÇÕES I AULA PRÁTICA MODULAÇÃO POR AMPLITUDE DE PULSOS 1. Introdução Como o sinal
UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA ELÉTRICA SISTEMAS DE TELECOMUNICAÇÕES I AULA PRÁTICA MODULAÇÃO POR AMPLITUDE DE PULSOS 1. Introdução Como o sinal
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Laboratório de Circuitos Elétricos II
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ ESCOLA POLITÉCNICA CURSO DE ENGENHARIA DE COMPUTAÇÃO DISCIPLINA DE CIRCUITOS ELÉTRICOS II NOME DO ALUNO: Laboratório de Circuitos Elétricos II Prof. Alessandro
PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ ESCOLA POLITÉCNICA CURSO DE ENGENHARIA DE COMPUTAÇÃO DISCIPLINA DE CIRCUITOS ELÉTRICOS II NOME DO ALUNO: Laboratório de Circuitos Elétricos II Prof. Alessandro
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
 Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
94 (8,97%) 69 (6,58%) 104 (9,92%) 101 (9,64%) 22 (2,10%) 36 (3,44%) 115 (10,97%) 77 (7,35%) 39 (3,72%) 78 (7,44%) 103 (9,83%)
 Distribuição das 1.048 Questões do I T A 94 (8,97%) 104 (9,92%) 69 (6,58%) Equações Irracionais 09 (0,86%) Equações Exponenciais 23 (2, 101 (9,64%) Geo. Espacial Geo. Analítica Funções Conjuntos 31 (2,96%)
Distribuição das 1.048 Questões do I T A 94 (8,97%) 104 (9,92%) 69 (6,58%) Equações Irracionais 09 (0,86%) Equações Exponenciais 23 (2, 101 (9,64%) Geo. Espacial Geo. Analítica Funções Conjuntos 31 (2,96%)
Capítulo 4 Resposta em frequência
 Capítulo 4 Resposta em frequência 4.1 Noção do domínio da frequência 4.2 Séries de Fourier e propriedades 4.3 Resposta em frequência dos SLITs 1 Capítulo 4 Resposta em frequência 4.1 Noção do domínio da
Capítulo 4 Resposta em frequência 4.1 Noção do domínio da frequência 4.2 Séries de Fourier e propriedades 4.3 Resposta em frequência dos SLITs 1 Capítulo 4 Resposta em frequência 4.1 Noção do domínio da
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2
 3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
UNIVERSIDADE FEDERAL DE SANTA MARIA - UFSM CENTRO DE TECNOLOGIA - CT DEPARTAMENTO DE ELETRÔNICA E COMPUTAÇÃO - DELC PROJETO REENGE - ENG.
 UNIVERSIDADE FEDERAL DE SANTA MARIA - UFSM CENTRO DE TECNOLOGIA - CT DEPARTAMENTO DE ELETRÔNICA E COMPUTAÇÃO - DELC PROJETO REENGE - ENG. ELÉTRICA CADERNO DIDÁTICO DE SISTEMAS DE CONTROLE 1 ELABORAÇÃO:
UNIVERSIDADE FEDERAL DE SANTA MARIA - UFSM CENTRO DE TECNOLOGIA - CT DEPARTAMENTO DE ELETRÔNICA E COMPUTAÇÃO - DELC PROJETO REENGE - ENG. ELÉTRICA CADERNO DIDÁTICO DE SISTEMAS DE CONTROLE 1 ELABORAÇÃO:
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Circuitos Elétricos Análise de Potência em CA
 Introdução Circuitos Elétricos Análise de Potência em CA Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Potência é a quantidade de maior importância em
Introdução Circuitos Elétricos Análise de Potência em CA Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Potência é a quantidade de maior importância em
Circuitos Elétricos Senoides e Fasores
 Circuitos Elétricos Senoides e Fasores Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Introdução Corrente contínua x corrente alternada. Ver War of Currentes
Circuitos Elétricos Senoides e Fasores Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Introdução Corrente contínua x corrente alternada. Ver War of Currentes
Circuitos de 2 ª ordem: RLC. Parte 1
 Circuitos de 2 ª ordem: RLC Parte 1 Resposta natural de um circuito RLC paralelo Veja circuito RLC paralelo abaixo: A tensão é a mesma e aplicando a soma de correntes que saem do nó superior temos: v R
Circuitos de 2 ª ordem: RLC Parte 1 Resposta natural de um circuito RLC paralelo Veja circuito RLC paralelo abaixo: A tensão é a mesma e aplicando a soma de correntes que saem do nó superior temos: v R
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias
 Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
As fases na resolução de um problema real podem, de modo geral, ser colocadas na seguinte ordem:
 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Introdução O Cálculo Numérico
1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Introdução O Cálculo Numérico
por séries de potências
 Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Figura 2.1: Carro-mola
 Capítulo 2 EDO de Segunda Ordem com Coeficientes Constantes 2.1 Introdução - O Problema Carro-Mola Considere um carro de massa m preso a uma parede por uma mola e imerso em um fluido. Colocase o carro
Capítulo 2 EDO de Segunda Ordem com Coeficientes Constantes 2.1 Introdução - O Problema Carro-Mola Considere um carro de massa m preso a uma parede por uma mola e imerso em um fluido. Colocase o carro
Cálculo Numérico Aula 1: Computação numérica. Tipos de Erros. Aritmética de ponto flutuante
 Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA SÉRIE DE EXERCÍCIO #A22 (1) O circuito a seguir amplifica a diferença de
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA SÉRIE DE EXERCÍCIO #A22 (1) O circuito a seguir amplifica a diferença de
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos. Prof. Cassiano Rech cassiano@ieee.org
 Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Matemática para Engenharia
 Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Circuitos Elétricos III
 Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 1 A resistência
Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 1 A resistência
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Aula 13 Análise no domínio da frequência
 Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
Circuitos Elétricos Circuitos de Segunda Ordem Parte 1
 Circuitos Elétricos Circuitos de Segunda Ordem Parte 1 Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Introdução Circuitos que contem dois elementos armazenadores
Circuitos Elétricos Circuitos de Segunda Ordem Parte 1 Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Introdução Circuitos que contem dois elementos armazenadores
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Só Matemática O seu portal matemático http://www.somatematica.com.br FUNÇÕES
 FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
Sistema de excitação
 Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
Associação de resistores
 Associação de resistores É comum nos circuitos elétricos a existência de vários resistores, que encontram-se associados. Os objetivos de uma associação de resistores podem ser: a necessidade de dividir
Associação de resistores É comum nos circuitos elétricos a existência de vários resistores, que encontram-se associados. Os objetivos de uma associação de resistores podem ser: a necessidade de dividir
ACIONAMENTOS ELETRÔNICOS (INVERSOR DE FREQUÊNCIA)
 ACIONAMENTOS ELETRÔNICOS (INVERSOR DE FREQUÊNCIA) 1. Introdução 1.1 Inversor de Frequência A necessidade de aumento de produção e diminuição de custos faz surgir uma grande infinidade de equipamentos desenvolvidos
ACIONAMENTOS ELETRÔNICOS (INVERSOR DE FREQUÊNCIA) 1. Introdução 1.1 Inversor de Frequência A necessidade de aumento de produção e diminuição de custos faz surgir uma grande infinidade de equipamentos desenvolvidos
Estabilidade no Domínio da Freqüência
 Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
1 Descrição do Trabalho
 Departamento de Informática - UFES 1 o Trabalho Computacional de Algoritmos Numéricos - 13/2 Métodos de Runge-Kutta e Diferenças Finitas Prof. Andréa Maria Pedrosa Valli Data de entrega: Dia 23 de janeiro
Departamento de Informática - UFES 1 o Trabalho Computacional de Algoritmos Numéricos - 13/2 Métodos de Runge-Kutta e Diferenças Finitas Prof. Andréa Maria Pedrosa Valli Data de entrega: Dia 23 de janeiro
2. Representação Numérica
 2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
a 1 x 1 +... + a n x n = b,
 Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
Aula 3. Carlos Amaral Fonte: Cristiano Quevedo Andrea
 Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
1 Problemas de transmissão
 1 Problemas de transmissão O sinal recebido pelo receptor pode diferir do sinal transmitido. No caso analógico há degradação da qualidade do sinal. No caso digital ocorrem erros de bit. Essas diferenças
1 Problemas de transmissão O sinal recebido pelo receptor pode diferir do sinal transmitido. No caso analógico há degradação da qualidade do sinal. No caso digital ocorrem erros de bit. Essas diferenças
1. CONTROLE DE PROCESSO
 1. CONTROLE DE PROCESSO PROCESSO: operação ou desenvolvimento que evolui progressivamente em direção a um resultado ou meta. Qualquer operação a ser controlada, tais como, processos químicos, biológicos,
1. CONTROLE DE PROCESSO PROCESSO: operação ou desenvolvimento que evolui progressivamente em direção a um resultado ou meta. Qualquer operação a ser controlada, tais como, processos químicos, biológicos,
Conforme explicado em 2.4.3, o sinal de voz x(n) às vezes é alterado com a adição de ruído r(n), resultando num sinal corrompido y(n).
 4 Wavelet Denoising O capítulo 3 abordou a questão do ruído durante a extração dos atributos as técnicas do SSCH e do PNCC, por exemplo, extraem com mais robustez a informação da voz a partir de um sinal
4 Wavelet Denoising O capítulo 3 abordou a questão do ruído durante a extração dos atributos as técnicas do SSCH e do PNCC, por exemplo, extraem com mais robustez a informação da voz a partir de um sinal
Conjuntos numéricos. Notasdeaula. Fonte: Leithold 1 e Cálculo A - Flemming. Dr. Régis Quadros
 Conjuntos numéricos Notasdeaula Fonte: Leithold 1 e Cálculo A - Flemming Dr. Régis Quadros Conjuntos numéricos Os primeiros conjuntos numéricos conhecidos pela humanidade são os chamados inteiros positivos
Conjuntos numéricos Notasdeaula Fonte: Leithold 1 e Cálculo A - Flemming Dr. Régis Quadros Conjuntos numéricos Os primeiros conjuntos numéricos conhecidos pela humanidade são os chamados inteiros positivos
Exercícios resolvidos P2
 Exercícios resolvidos P Questão 1 Dena as funções seno hiperbólico e cosseno hiperbólico, respectivamente, por sinh(t) = et e t e cosh(t) = et + e t. (1) 1. Verique que estas funções satisfazem a seguinte
Exercícios resolvidos P Questão 1 Dena as funções seno hiperbólico e cosseno hiperbólico, respectivamente, por sinh(t) = et e t e cosh(t) = et + e t. (1) 1. Verique que estas funções satisfazem a seguinte
Aplicações com OpAmp. 1) Amplificadores básicos. Amplificador Inversor
 225 Aplicações com OpAmp A quantidade de circuitos que podem ser implementados com opamps é ilimitada. Selecionamos aqueles circuitos mais comuns na prática e agrupamos por categorias. A A seguir passaremos
225 Aplicações com OpAmp A quantidade de circuitos que podem ser implementados com opamps é ilimitada. Selecionamos aqueles circuitos mais comuns na prática e agrupamos por categorias. A A seguir passaremos
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções
 Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
