Universidade Federal de Santa Catarina
|
|
|
- Ronaldo Castro Leveck
- 8 Há anos
- Visualizações:
Transcrição
1 Universidade Federal de Santa Catarina Programa de Pós-Graduação em Engenharia de Produção APLICAÇÃO DOS FRACTAIS AO MERCADO DE CAPITAIS UTILIZANDO-SE AS ELLIOTT WAVES Dissertação de Mestrado André Daniel Hayashi Florianópolis 2002
2 André Daniel Hayashi APLICAÇÃO DOS FRACTAIS AO MERCADO DE CAPITAIS UTILIZANDO-SE AS ELLIOTT WAVES Dissertação apresentada ao Programa de Pós- Graduação em Engenharia de Produção da Universidade Federal de Santa Catarina como requisito parcial para obtenção do título de Mestre em Engenharia de Produção, Área de concentração Mídia em Conhecimento - ênfase em Tecnologia Educacional. Orientadora: Profª Christianne Coelho de Souza Reinisch Coelho, Drª Florianópolis, abril de 2002
3 ii André Daniel Hayashi APLICAÇÃO DOS FRACTAIS AO MERCADO DE CAPITAIS UTILIZANDO-SE AS ELLIOTT WAVES Esta dissertação foi julgada e aprovada para a obtenção do título de Mestre em Engenharia de Produção no Programa de Pós-Graduação em Engenharia de Produção - Área de Concentração: Mídia e Conhecimento - ênfase em Tecnologia Educacional da Universidade Federal de Santa Catarina. Florianópolis, 11 de abril de Prof. Ricardo Miranda Barcia, Ph.D. Coordenador do Curso de Pós-Graduação em Engenharia de Produção Banca examinadora: Profª Christianne Coelho de Souza Reinisch Coelho, Drª Orientadora Prof. Francisco Antônio Pereira Fialho, Dr. Prof. Luis Alberto Palma e Almeida Pinheiro, Ms. Prof. Luis Alberto Gomes, Dr. Prof. Luiz Fernando Gonçalves de Figueiredo, Dr.
4 iii Para Alexandra e Luis Henrique, pelo amor incondicional. Para Luis Pinheiro, um guia nos mercados financeiros, um segundo pai nas horas vagas. Para Germano Probst, pessoa mais iluminada e carismática da família, exemplo de humildade e sabedoria, sempre ao nosso lado nas decisões mais difíceis.
5 iv SUMÁRIO RESUMO... vi ABSTRACT... vii LISTA DE FIGURAS... viii 1 INTRODUÇÃO Objetivos Metodologia Hipóteses Justificativa BASE TEÓRICA Teorias do Caos e da Complexidade Termos Científicos de Relevância Do Caos aos Fractais Teoria dos Fractais Estrutura Fina Auto Similaridade Simplicidade da Lei de Formação Dimensão Fractal Elliott Waves Mercados de Capitais Bolsas de Valores Bolsas de Mercadorias e Futuros Forças que Atuam nos Mercados O Comportamento dos Preços Evolução Econômica e a Complexidade CONHECIMENTOS APLICADOS Aplicação dos Fractais nos Mercados Financeiros O Princípio das Ondas Elliott O modelo das Cinco Ondas Os Padrões de Onda O Ciclo Completo... 71
6 v Escalas da Onda Exemplo de Construção Fractal Análise Detalhada das Estruturas ou Padrões de Ondas Elliott O Padrão Impulso Padrões Corretivos Combinações entre Correções Regras Lógicas Pós-construção Previsões mais Detalhadas Estado da Arte CONCLUSÕES SUGESTÕES PARA FUTUROS TRABALHOS REFERÊNCIAS ANEXO 1 - ÍNDICE DA DOW JONES COM OS RESPECTIVOS INDICADORES TÉCNICOS
7 vi RESUMO HAYASHI, André D. Aplicação dos fractais ao mercado de capitais utilizando-se as Elliott Waves. Florianópolis, f. Dissertação (Mestrado em Engenharia de Produção) - Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal de Santa Catarina. Esta pesquisa apresenta o método Elliott Waves de previsão dos próximos movimentos de preços no mercado financeiro sob o enfoque da teoria do caos e da complexidade, novas áreas da ciência que procuram entender o que a física newtoniana ainda não conseguiu explicar: o comportamento dos sistemas complexos. A possibilidade de conexão entre os mercados de capitais e as teorias do caos e da complexidade foi motivada pela descoberta do comportamento fractal das séries temporais de preços por Benoit Mandelbrot (1997) e pelos registros de repetições quase perfeitas de padrões fractais nos gráficos históricos de ações e mercadorias referentes à bolsa de valores Nova York e à bolsa de mercadorias de Chicago, feitos por Ralph Nelson Elliott e relatados por Robert Prechter (2000) e Glenn Neely (1990). Como alternativa à tradicional Hipótese dos Mercados Eficientes (HME), que está para a Economia assim como a mecânica de Newton está para a Física, a modelagem matemática através dos fractais produz resultados que acompanham as mudanças reais nos preços de uma maneira mais precisa e explicam o comportamento do mercado nos momentos de maior volatilidade. Enquanto os fractais Elliott baseiam-se em dados históricos para se prever acontecimentos futuros, a HME tem como uma de suas premissas a inexistência de memória nos mercados, ou seja, os preços variam aleatoriamente (distribuição de Gauss) e unicamente em função dos novos eventos econômicos, já que os eventos passados já foram totalmente assimilados pelo mercado e descontados nos preços atuais. A HME não corresponde à realidade dos mercados financeiros, o que foi comprovado por esta dissertação. Palavras-chave: mercado de capitais; elliott waves; fractais; complexidade.
8 vii ABSTRACT HAYASHI, André D. Aplicação dos fractais ao mercado de capitais utilizando-se as Elliott Waves. Florianópolis, f. Dissertação (Mestrado em Engenharia de Produção) - Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal de Santa Catarina. This research presents the Elliott Waves principle for financial markets forecasting, under the view of chaos and complexity theories, new scientific fields that try to understand what newtonian physics still can not explain: the complex systems behavior. The possibility of connection between the financial markets and chaos and complexity theories was motivated by Benoit Mandelbrot (1997), the fractal behavior discoverer in the price movements, and by Ralph Nelson Elliott, Robert Prechter (2000) and Glenn Neely (1990), for the record of almost perfect fractal patterns recurrence in stock and commodities charts of NYSE and CBOT. Unlike the Efficient Market Hypothesis (EMH), that is the economic version of the newtonian mechanics, the mathematical modeling with fractals produces results that follow the real price changes more precisely and explain the market behavior in the moments of critical volatility. While Elliott fractals are based on historical data to predict future events, EMH is based on the absence of memory in the markets, i.e., the prices move at random (random walk, Gaussian curve), only as a function of new economics events, and the past events had already been incorporated by the market and discounted on the actual prices. The EMH does not correspond with the market reality, what was confirmed by this dissertation. Key-words: financial markets; elliott Waves; fractals; complexity.
9 viii LISTA DE FIGURAS 1 DIAGRAMA DE FEIGENBAUM E CONJUNTO DE MANDELBROT UMA SIMULAÇÃO DO EXPERIMENTO DE LORENZ CARACTERIZANDO O AUMENTO EM CASCATA DO ERRO COM O PASSAR DO TEMPO RODA D ÁGUA LORENZIANA PRIMEIRAS ÓRBITAS NO ESPAÇO DE FASE DO SISTEMA DE LORENZ ATRATOR ESTRANHO DE LORENZ A CURVA DE KOCH FLOCO DE NEVE DE KOCH AUTO SIMILARIDADE NA COUVE-FLOR SAZONALIDADE DE RAÇAO DE SOJA DISTRIBUIÇÃO NORMAL E LEPTOCÚRTICA CURVA DA RENDA EM FUNÇÃO DO PERCENTUAL DE FAMÍLIAS TRÊS SÉRIES TEMPORAIS DO ÍNDICE S&P GERADOR DE 3 ONDAS OPERAÇÃO UNIFRACTAL PARA MULTIFRACTAL AUMENTO DA VOLATILIDADE DESENHO ANIMADO DE MOVIMENTO BROWNIANO APÓS VÁRIAS INTERPOLAÇÕES DESENHO ANIMADO DO MOVIMENTO BROWNIANO PRODUZIDO DE MANEIRA MULTIFRACTAL O MODELO BÁSICO O CICLO COMPLETO EXEMPLO DE CICLO COMPLETO DE ESCALA INTERMEDIATE CICLO COMPLETO DE ESCALA CYCLE DIVISÃO DO DNA NA RAZÃO ÁUREA EXTENSÕES ÍNDICE DOW JONES DE BULL MARKET TRUNCATION REGRA DA SOBREPOSIÇÃO NUM IMPULSO TENDÊNCIA REGRA DA SOBREPOSIÇÃO NUM IMPULSO TERMINAL REQUISITOS DE UMA ESTRUTURA FLAT... 85
10 ix 29 LIMITES DO ZIGZAG TRIÂNGULOS COMBINAÇÃO ENTRE ZIGZAG E FLAT COMBINAÇÃO DUPLO TRÊS PREVISÃO DO ÍNDICE DOW JONES POR GLENN NEELY CONFIRMAÇÃO DO TÉRMINO DE UM IMPULSO CONFIRMAÇÃO DO TÉRMINO DE UM ZIGZAG OU FLAT CONFIRMAÇÃO DE TÉRMINO DE UM FLAT CONFIRMAÇÃO DE UM TRIÂNGULO CONVERGENTE VARIAÇÕES DE CORREÇÕES ELLIOTT WAVE ANALYZER II SOFTWARE COMPROVANTE DO RECEBIMENTO DA CARTA COM PROPOSTA DE SERVIÇO FLASH!
11 1 1 INTRODUÇÃO A teoria da complexidade, que assume o desafio de abordar de uma maneira muito mais realista os processos dinâmicos complexos, vem fascinando cientistas das mais diversas áreas do conhecimento. Matemática, física, química, biologia, computação, economia, psicologia e antropologia podem ser consideradas as principais, que de maneira transdisciplinar tornam possível a emergência de novas ciências, dentre elas a teoria do caos. Esta transdisciplinaridade possibilitou o aparecimento de novas ferramentas e termos científicos de relevância na atualidade, como dimensão fractal, atratores, efeito borboleta, entre outros. Fractais são estruturas matemáticas, que se repetem infinitamente quando vistas numa escala cada vez menor. Na década de 1980, Benoit Mandelbrot provou a existência dos fractais em seu livro "The Fractal Geometry of Nature". Mandelbrot reconheceu a estrutura fractal em numerosos objetos e formas da natureza. Mais recentemente, Mandelbrot descobriu a possibilidade de modelar o mercado financeiro através dos fractais. O princípio das ondas Elliott, foi descoberto no final da década de 1920, por Ralph Nelson Elliott. Tal princípio diz que o comportamento social avança e recua em padrões reconhecíveis. Utilizando o mercado de ações como a sua principal ferramenta de pesquisa, Elliott descobriu que o caminho das mudanças nos preços das ações revela um esquema estrutural comparável à simples harmonia encontrada na natureza. Em outras palavras, Elliott reconheceu que o mercado financeiro movese em ondas. Isto é, move se em padrões ou ciclos aproximadamente repetitivos, que refletem as ações e emoções humanas causadas por influências externas ou pela psicologia das massas. O fluxo e refluxo do pensamento coletivo segue o mesmo padrão de repetição das ondas do mercado financeiro. Em parte, Elliott baseou seu trabalho na teoria Dow, que também define o movimento de preços em termos de ondas, mas foi além, descobrindo a natureza fractal dos mercados. Elliott analisou os mercados com maior profundidade, identificando as características específicas de cada padrão de onda e fazendo
12 2 previsões detalhadas dos próximos movimentos da bolsa de valores baseadas nos padrões que ele havia previamente encontrado. Elliott isolou padrões de movimentos, ou ondas, que aparecem nos valores dos preços das ações e que são repetitivos em forma, mas não necessariamente repetitivos no tempo e em amplitude. Ele nomeou, definiu e ilustrou estas ondas. Então, descreveu como estas estruturas se juntam para formar versões maiores dos mesmos padrões, como estes por sua vez se ligam para formar novos modelos, semelhantes aos anteriores só que de maior tamanho, e assim por diante. Isto é o que caracteriza a natureza fractal do princípio de Elliott. Nos anos 70, o princípio da onda ganhou popularidade através do trabalho de Frost e Prechter. Eles publicaram o livro "Elliott wave principle, key to stock market profits" (1978) que se tornou um clássico sobre as ondas Elliott, no qual eles previram, no meio da crise dos anos 70, a grande elevação nas cotações em bolsa nos anos 80. Não só previram corretamente a alta nos mercados, mas Prechter também previu a queda em O estudo das ondas Elliott ganhou profundidade e objetividade com o livro "Mastering the Elliott Wave", resultado de um exaustivo trabalho de dez anos desenvolvido por Glenn Neely (1990), um experiente analista dos mercados financeiros que catalogou de maneira muito criteriosa e detalhada as características de cada onda e estudou mais a fundo o aparecimento de aglomerados de ondas mais complexos. Em seu tempo, Elliott demorou anos para detectar os padrões que ele mesmo cunhou no mercado de ações. Paralelamente, baseou também suas previsões de mercado na série matemática dos números de Fibonacci. Todo o seu conhecimento foi publicado em vários livros, que deram os fundamentos para pessoas como Frost, Prechter, Neely e outros analistas produzissem programas em computador para previsões dos próximos movimentos do mercado não só de ações, mas de qualquer mercado de capitais.
13 3 É importante destacar que as previsões fornecidas pelos programas de computador não são pontuais, isto é, estão sempre agregadas a uma probabilidade de erro. A preocupação de alguns analistas que elaboram os modelos matemáticos que determinam cada programa é de que se aproximem cada vez mais da perfeição, ou seja, 100% de acerto dos próximos movimentos de qualquer bolsa de valores. Esta dissertação alertará estes analisas que tal façanha é impossível e que a riqueza de possibilidades de mudança no mercado financeiro é a mesma de qualquer sistema complexo da natureza. E as teorias do caos e da complexidade são as mais realistas no estudo dos sistemas da natureza, onde há permissão para o erro e encontram-se sinais para iminentes mudanças. Pergunta de pesquisa De que forma as Elliott Waves podem ajudar uma equipe de analistas técnicos a prever os próximos movimentos do mercado financeiro? 1.1 Objetivos O objetivo da dissertação é mostrar que as teorias do caos e da complexidade são úteis no estudo do comportamento dos preços de ativos nos mercados de capitais. Especificamente, pretende-se mostrar como os fractais e a teoria das Elliott Waves podem auxiliar uma equipe de analistas na previsão de alta ou queda nos mercados financeiros. É importante deixar claro que as bolsas de valores ou de mercadorias não existem apenas por motivos especulativos. As bolsas de valores são necessárias para que as empresas que vendem ações possam captar recursos e investir em novos projetos e empreendimentos. Ou seja, são imprescindíveis para o crescimento econômico e geração de novos empregos. Os especuladores compram as ações com o intuito que elas valorizem, mas sem eles não haveria liquidez no mercado acionário. As bolsas de mercadorias e futuros existem para proteger os produtores e exportadores (hedgers) da oscilação nos preços de suas mercadorias. O risco da oscilação dos
14 4 preços é repassado aos especuladores. Até mesmo um simples produtor rural do interior do Estado do Paraná pode se proteger da queda no preço dos grãos, contratando uma cooperativa ou uma corretora que fará em nome do produtor uma operação de hedging junto à bolsa de mercadorias de Chicago. Neste contexto, os métodos de previsão dos próximos acontecimentos nas bolsas possibilitam que hedgers e especuladores, aconselhados por analistas, assumam posições melhores no mercado financeiro, evitando-se prejuízos sucessivos e queda na liquidez. A liquidez é fundamental para que os mercados exerçam eficazmente as suas principais funções, quais sejam, o crédito às empresas e a proteção à variação dos preços. 1.2 Metodologia maneira: Os trabalhos referentes a esta dissertação podem ser divididos da seguinte ƒ Revisão bibliográfica sobre a teoria do caos, a teoria da complexidade e a geometria dos fractais. ƒ Pesquisa sobre os trabalhos interdisciplinares de Benoit Mandelbrot, Brain Arthur e Edgar Peters que relacionam as teorias previamente pesquisadas com o mercado financeiro. ƒ ƒ Fazer a conexão entre o trabalho de Mandelbrot e as Elliott Waves Aprendizado do método de previsão das ondas Elliott, baseando-se nos trabalhos de Robert Prechter e Glenn Neely, com o intuito de se responder à pergunta de pesquisa. 1.3 Hipóteses Os preços das ações e commodities não se comportam segundo a Hipótese dos Mercados Eficientes (HME), versão econômica das leis de Newton, segundo a qual: a) os investidores reagem à informação assim que é recebida, não esperando que ela se torne uma tendência baseada numa série cumulativa de eventos. A HME não leva em conta a história dos eventos passados para
15 5 se projetar os preços futuros, pois num mercado eficiente, todo histórico de fatos já foi assimilado pelo mercado, e apenas fatos novos inesperados podem modificar o rumo dos preços. Não há memória nos mercados eficientes, ou seja, os preços são independentes, levando matemáticos do ramo da estatística a modelá-los como passeios aleatórios (random walk), de aspecto parecido ao movimento browniano da física, onde a distribuição de probabilidade dos preços, segundo Adolphe Quetelet (1900), citado por Gleiser (2002), corresponde à curva normal de Gauss. b) o agente homo sapiens não tem identidade própria, reduzindo-se a homo economicus: decisor racional que busca defender seus interesses, utilizandose de sua capacidade ilimitada de cálculo e de plena informação. Esta hipótese pressupõe que todos têm a mesma capacidade matemática e o mesmo acesso a notícias, ou seja, os investidores são homogêneos. Esta dissertação baseia-se na hipótese de que o mercado financeiro possui memória, é um sistema complexo adaptativo que, para garantir sua sobrevivência, situa-se na margem entre a ordem e o acaso. Os investidores reagem à informação de forma diferenciada, agindo precipitadamente ou se adaptando à opinião de outros. Quando, a partir de dados passados e constante aprendizagem, forma-se uma mesma opinião (ordem) por parte de uma maioria, tendências de queda ou subida podem impulsionar o mercado para baixo ou para cima respectivamente, não apenas por motivos inesperados (acaso). O resultado disso é que o passeio aleatório referido anteriormente se transforma num passeio aleatório com tendência (enviezado), ou movimento browniano fraccional (Mandelbrot, 1997). Existe uma certa ordem por traz da aparente desordem nos mercados de capitais. O princípio das Elliott Waves está de acordo com esta última hipótese, baseada nos trabalhos científicos de Stuart Kauffman, Brian Arthur, Benoit Mandelbrot, Edgar Peters, e também nos trabalhos de cunho mais empírico de Ralph Nelson Elliott, Robert R Prechter, e Glenn Neely, com lastro de décadas de experiência e registro de dados nos mercados financeiros.
16 6 1.4 Justificativa O estudo dos sistemas dinâmicos não lineares e da teoria da complexidade é o estudo da turbulência. Mais precisamente, é o estudo da transição da estabilidade para a instabilidade. Esta transição está toda em nossa volta. Aparece na corrente da fumaça do cigarro que quebra em redemoinhos de fumaça e dissipa pelo ar. Ocorre quando coloca-se creme no café ou quando ferve-se água. Ainda, este evento de transição de um estado estável para um estado de turbulência não pode ser modelado pela tradicional física newtoniana. A física newtoniana pode prever onde o planeta Marte estará daqui a três séculos, mas não consegue prever as condições exatas do clima de amanhã. Por considerar que todos os sistemas físicos podem ser estudados como a soma linear de suas partes, reduzindo-se o problema total ao estudo mais simplificado de seus componentes, como engrenagens mecânicas de um relógio, a física de Newton também é conhecida por teoria mecanicista ou reducionista, e baseia-se em três princípios: para cada causa, existe um efeito direto. a) Todos os sistemas procuram um equilíbrio onde o sistema está em repouso. b) A natureza é ordenada. Newton deixou um enorme conhecimento. Sua física e o cálculo que ele desenvolveu para prová-la permanecem como algumas das máximas realizações da humanidade. Através da matemática, pode-se entender e prever como agirão corpos em movimento. Há limites entretanto. A física de Newton pode explicar como dois corpos interagem, mas não pode prever a interação, por exemplo, entre três corpos. O problema dos três corpos ocupou cientistas na maior parte do século 19. Neste mesmo século, Henri Poincaré descobriu que o problema não poderia ser resolvido
17 7 para uma única solução, devido às não linearidades inerentes ao sistema. Poincaré, citado por Edgar E. Peters (1996, p.137) explicou porque estas não linearidades eram importantes: Uma pequena causa que nos passa desapercebida, determina um considerável efeito que não perdemos de vista, e então dizemos que o efeito é devido ao acaso [...]. Pode acontecer de pequenas diferenças nas condições iniciais produzirem grandes diferenças no final do fenômeno. Um pequeno erro no início produzirá um enorme erro posteriormente. Previsão torna-se impossível [...]. Este efeito é agora conhecido como sensível dependência das condições iniciais, ou efeito borboleta, e se tornou uma importante característica dos sistemas dinâmicos. Um sistema dinâmico é inerentemente imprevisível no longo prazo. Previsões com 100% de exatidão calculadas a partir das equações lineares newtonianas é o paradigma questionado pelas teorias do caos e da complexidade. Acompanhando os ideais do Instituto de Santa Fé ( muitos grupos científicos até mesmo empresas financeiras estão desenvolvendo uma cultura transdisciplinar, que apoiada na estatística, na computação, na economia e na psicologia, pode produzir novos conceitos e ferramentas para o estudo dos sistemas dinâmicos complexos, ou seja, a grande maioria dos sistemas presentes na natureza e nas relações humanas. Inclui-se neste contexto o mercado de capitais, onde a tradicional Hipótese dos Mercados Eficientes (HME) é uma abordagem linear insuficiente para explicar a complexidade dos movimentos dos preços e tendências na economia mundial e local. Em outras palavras, a HME está para os mercados financeiros assim como a teoria newtoniana está para os sistemas complexos. O economista Ilan Gleiser (2002, p.211) escreve sobre a ineficiência da HME em seu livro "Caos e complexidade": Desde a origem de Wall Street até agora, os investidores vêm tentando decifrar os segredos do movimento das ações. Quais são os melhores investimentos? Quais ativos vão subir e quais vão cair? É possível controlar o risco? O comportamento dos
18 8 preços no passado influi no comportamento futuro? A maioria dos modelos criados para responder a essas perguntas tem essência linear e ainda hoje são os mais usados, mas apesar disso, não conseguem representar fielmente o que acontece nos mercados financeiros e apresentam falhas. Por isso a importância da incorporação da nova Teoria do Caos/Complexidade na ciência econômica e nas finanças. Ela representa o mercado com mais precisão e vem revolucionar o paradigma atual: a Hipótese de Mercado Eficiente, segundo a qual os investidores reagem à informação assim que é recebida, não esperando que ela se torne uma tendência baseada numa série cumulativa de eventos. A HME não leva em consideração a história, uma vez que, em um mercado eficiente, toda a informação já está descontada nos preços correntes dos ativos.[...] O modelo de mercado eficiente reduz o agente [homo sapiens] ao homo economicus: decisor racional que busca defender seus interesses, utilizando-se de sua capacidade ilimitada de cálculo e de plena informação. Esta hipótese pressupõe que todos têm a mesma capacidade matemática e o mesmo acesso a notícias. Todos os investidores são homogêneos. Justifica-se portanto a utilização de novas ferramentas que levam em conta os novos conceitos do caos e da complexidade para o estudo dos mercados de capitais. Neste trabalho será feita especificamente uma análise da eficácia da aplicação do princípio das ondas Elliott na previsão de quedas e subidas de preços futuros. Este princípio não se encaixa na HME e encontra fundamentos no caos/complexidade porque: a) Utiliza eventos passados - padrões históricos de preços registrados por Ralph Elliott desde o início do funcionamento das bolsas de valores e mercadorias para se prever eventos futuros. b) Baseia-se na emergência de uma "psicologia das massas". Raciocinandose de uma maneira fractal, onde características semelhantes ocorrem em várias escalas, pode-se constatar que: assim como o cérebro humano é um sistema complexo formado por vários agentes de identidade única, que por auto-organização relacionam-se e contribuem não linearmente para a emergência de memória, consciência e aprendizado, o mercado financeiro é um sistema complexo, onde cada investidor é um ser humano único, que
19 9 não reage linearmente as notícias, pois relaciona-se com outros investidores, e dependendo do nível de adaptação, aprendizado e experiência sobre notícias passadas que possua, pode tomar uma decisão precipitada ou esperar e seguir a maioria, realimentando positivamente esta maioria até que uma "massa pensante" tenha uma mesma opinião, emergindo uma tendência de subida ou descida dos preços do mercado.
20 10 2 BASE TEÓRICA 2.1 Teorias do Caos e da Complexidade O mercado de capitais é regido pelas decisões humanas, que por sua vez são influenciadas por variáveis internas e externas. Dentre as variáveis internas pode-se citar o medo, a insegurança, a velocidade com que os investidores decidem comprar ou vender contratos. No caso das variáveis externas, pode-se citar a taxa de juros, as taxas de câmbio, até mesmo fatores naturais como o clima, já que muitas commodities, como milho e soja, sofrem alteração de preço após uma tempestade ou estiagem. Em decorrência do elevado número de graus de liberdade, ou seja, de muitas variáveis em questão, pode-se dizer que os mercados de capitais são sistemas complexos e que para estudá-los é necessário interdisciplinaridade. A ciências do caos e da complexidade, além de embasarem-se em várias disciplinas, criaram novos termos e possibilidades, atingindo um nível transdiciplinar de entendimento dos vários processos naturais aparentemente dominados pela total desordem. Um dos objetivos desta seção é dar clareza a alguns termos científicos utilizados no estudo dos sistemas dinâmicos complexos. Serão escolhidos apenas aqueles termos que têm relevância para esta dissertação. O segundo e último objetivo será a composição de um resumo dos acontecimentos relativos à ciência do caos que possuem maior peso no embasamento teórico deste trabalho, até atingir-se o conceito considerado de maior importância para que economistas encontrem ordem na desordem dos fluxos econômicos, o atrator estranho Termos Científicos de Relevância Este item tem o objetivo de auxiliar na leitura e interpretação do restante desta dissertação, através da conceituação de termos científicos de fundamental importância para a visualização do comportamento dos sistemas dinâmicos complexos.
21 11 Segundo Ilan Gleiser (2002, p.55), caos e complexidade são fenômenos interconectados porém distintos. Existe um certo debate em relação ao significado técnico e campo de influência dos dois fenômenos. Alguns argumentam que caos é uma teoria geral que engloba o estudo de sistemas complexos. Outros argumentam exatamente o oposto, ou seja, que a teoria do caos é uma aplicação específica de uma teoria maior que estuda os sistemas dinâmicos, a ciência da complexidade. Outros não vêm nenhuma diferença entre os dois. A definição mais aceita é a de que os dois fenômenos são complementares. A teoria da complexidade é o estudo de como um sistema de equações muito complicadas pode gerar padrões de comportamento bastante simples e ordenados para certos valores dos parâmetros destas equações. Já a teoria do caos estuda como equações não lineares simples geram comportamento complicado. Fenômenos complexos ocorrem precisamente no ponto crítico de transição da ordem para o caos. Um sistema em estado complexo está no limiar do caos (the edge of chaos), na borda entre um comportamento periódico previsível e o comportamento caótico, que pode ser determinístico ou não, dependendo do sistema. Para Edward N. Lorenz (1993, p.7), uma seqüência de eventos é determinística quando tem-se certeza de qual é o próximo evento desta seqüência; isto é, sua evolução é governada por leis precisas. Seqüência aleatória ou randômica é caracterizada pela ausência de determinismo. A teoria do caos determinístico é um conceito relativamente novo em ciência. A palavra caos, segundo o dicionário da língua portuguesa de Aurélio Buarque de Hollanda Ferreira, significa um vazio obscuro e ilimitado que antecede e teria propiciado a geração do mundo, o caos primordial que o livro de Gênesis se refere. Em uma segunda definição seria uma grande confusão ou desordem. O termo caos determinístico é aparentemente paradoxal. Como algo pode ser caótico e determinístico ao mesmo tempo? De forma simples, é a idéia de que se pode obter resultados aparentemente aleatórios a partir de simples equações matemáticas. Mas
22 12 na teoria do caos também se encontra o oposto: é possível achar ordem onde aparentemente só há aleatoriedade, dando margem para que muitos a confundam com a teoria da complexidade. Mas enquanto a teoria do caos encontra ordem na aparente desordem total nas ondas temporais de Lorenz, nos atratores estranhos, nos diagramas de estado final de Feigenbaum (figura 1, desenho superior), no conjunto de Mandelbrot (figura 1, desenho inferior) e em outros resultados matemáticos que vem surgindo, a teoria da complexidade estuda a emergência de estados ordenados a partir da auto-organização, adaptabilidade, aprendizado, entropia e realimentação positiva dos agentes constituintes do sistema complexo. FIGURA 1 - DIAGRAMA DE FEIGENBAUM E CONJUNTO DE MANDELBROT FONTE: PEITGEN, et al. (1992) Lorenz (1993) afirma também que a palavra caos não possui ainda uma definição final, e recentemente vem tomando o lugar de outras palavras adquirindo vários
23 13 significados técnicos relacionados mas distintos. Sua definição para sistemas caóticos: são sistemas determinísticos - ou quase determinísticos devido à presença de uma leve quantidade de aleatoriedade - mas que não parecem ser determinísticos, ou seja, aparentemente são puramente randômicos. Como exemplos de fenômenos supostamente caóticos pode-se citar o movimento de queda das folhas de uma árvore, a evolução populacional de uma espécie, as flutuações do clima terrestre, o funcionamento do cérebro, as flutuações dos preços das ações na bolsa de valores. No contexto da teoria do caos, tais sistemas são estudados da maneira mais realista possível, estando sujeitos a possíveis modificações causadas por eventos aleatórios externos. Esses sistemas possuem portanto uma leve aleatoriedade devido a eventos exteriores que surgem ao acaso, entretanto, a maior parte da aparente randomicidade do sistema não é produto da verdadeira aleatoriedade exterior. Isto é, processos do mundo real que aparentemente se comportam randomicamente talvez a folha em queda ou as flutuações da bolsa poderiam ser classificados de caóticos, já que eles continuariam a parecer randômicos mesmo que a verdadeira aleatoriedade a passagem de uma pessoa perto da folha em queda ou um ataque terrorista à bolsa de valores pudesse de alguma maneira ser eliminada. A aleatoriedade aparente nos sistemas determinísticos caóticos ocorre devido ao acúmulo não linear de erros de arredondamento, fato que será explicado com mais detalhes no item deste trabalho. Para Gleiser (2002, p.23), a teoria do caos é o estudo de comportamentos instáveis e aperiódicos em sistemas dinâmicos determinísticos não lineares. Aborda-se agora o conceito de sistemas dinâmicos. Uma definição matemática de sistemas dinâmicos é dada por Elizabeth Karas e Celso P. Cerra (1997, p.77): Sendo C o conjunto dos números complexos, seja f de C em C uma função contínua da variável complexa z. Vamos instituir um processo que produza uma sequência de
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
6 Construção de Cenários
 6 Construção de Cenários Neste capítulo será mostrada a metodologia utilizada para mensuração dos parâmetros estocásticos (ou incertos) e construção dos cenários com respectivas probabilidades de ocorrência.
6 Construção de Cenários Neste capítulo será mostrada a metodologia utilizada para mensuração dos parâmetros estocásticos (ou incertos) e construção dos cenários com respectivas probabilidades de ocorrência.
O céu. Aquela semana tinha sido uma trabalheira! www.interaulaclube.com.br
 A U A UL LA O céu Atenção Aquela semana tinha sido uma trabalheira! Na gráfica em que Júlio ganhava a vida como encadernador, as coisas iam bem e nunca faltava serviço. Ele gostava do trabalho, mas ficava
A U A UL LA O céu Atenção Aquela semana tinha sido uma trabalheira! Na gráfica em que Júlio ganhava a vida como encadernador, as coisas iam bem e nunca faltava serviço. Ele gostava do trabalho, mas ficava
UNIVERSIDADE DE SÃO PAULO E S C O L A D E A R T E S, C I Ê N C I A S E H U M A N I D A D E
 UNIVERSIDADE DE SÃO PAULO E S C O L A D E A R T E S, C I Ê N C I A S E H U M A N I D A D E Trabalho proposto pela disciplina de Orientado por Professor Dr. Fernando Coelho Mário Januário Filho 5365372
UNIVERSIDADE DE SÃO PAULO E S C O L A D E A R T E S, C I Ê N C I A S E H U M A N I D A D E Trabalho proposto pela disciplina de Orientado por Professor Dr. Fernando Coelho Mário Januário Filho 5365372
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
1. Introdução. 1.1 Introdução
 1. Introdução 1.1 Introdução O interesse crescente dos físicos na análise do comportamento do mercado financeiro, e em particular na análise das séries temporais econômicas deu origem a uma nova área de
1. Introdução 1.1 Introdução O interesse crescente dos físicos na análise do comportamento do mercado financeiro, e em particular na análise das séries temporais econômicas deu origem a uma nova área de
AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA
 CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
Modelo Cascata ou Clássico
 Modelo Cascata ou Clássico INTRODUÇÃO O modelo clássico ou cascata, que também é conhecido por abordagem top-down, foi proposto por Royce em 1970. Até meados da década de 1980 foi o único modelo com aceitação
Modelo Cascata ou Clássico INTRODUÇÃO O modelo clássico ou cascata, que também é conhecido por abordagem top-down, foi proposto por Royce em 1970. Até meados da década de 1980 foi o único modelo com aceitação
MÓDULO 6 INTRODUÇÃO À PROBABILIDADE
 MÓDULO 6 INTRODUÇÃO À PROBBILIDDE Quando estudamos algum fenômeno através do método estatístico, na maior parte das vezes é preciso estabelecer uma distinção entre o modelo matemático que construímos para
MÓDULO 6 INTRODUÇÃO À PROBBILIDDE Quando estudamos algum fenômeno através do método estatístico, na maior parte das vezes é preciso estabelecer uma distinção entre o modelo matemático que construímos para
Glossário de Dinâmica Não-Linear
 Glossário de Dinâmica Não-Linear Dr. Fernando Portela Câmara, MD, PhD Coordenador do Depto. Informática da ABP (2004-2007) Atrator O estado no qual um sistema dinâmico eventualmente se estabiliza. Um atrator
Glossário de Dinâmica Não-Linear Dr. Fernando Portela Câmara, MD, PhD Coordenador do Depto. Informática da ABP (2004-2007) Atrator O estado no qual um sistema dinâmico eventualmente se estabiliza. Um atrator
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
Logística e a Gestão da Cadeia de Suprimentos. "Uma arma verdadeiramente competitiva"
 Logística e a Gestão da Cadeia de Suprimentos "Uma arma verdadeiramente competitiva" Pequeno Histórico No período do pós-guerra até a década de 70, num mercado em franca expansão, as empresas se voltaram
Logística e a Gestão da Cadeia de Suprimentos "Uma arma verdadeiramente competitiva" Pequeno Histórico No período do pós-guerra até a década de 70, num mercado em franca expansão, as empresas se voltaram
Gestão do Conhecimento A Chave para o Sucesso Empresarial. José Renato Sátiro Santiago Jr.
 A Chave para o Sucesso Empresarial José Renato Sátiro Santiago Jr. Capítulo 1 O Novo Cenário Corporativo O cenário organizacional, sem dúvida alguma, sofreu muitas alterações nos últimos anos. Estas mudanças
A Chave para o Sucesso Empresarial José Renato Sátiro Santiago Jr. Capítulo 1 O Novo Cenário Corporativo O cenário organizacional, sem dúvida alguma, sofreu muitas alterações nos últimos anos. Estas mudanças
ASTRONOMIA. A coisa mais incompreensível a respeito do Universo é que ele é compreensível Albert Einstein
 ASTRONOMIA A coisa mais incompreensível a respeito do Universo é que ele é compreensível Albert Einstein ASTRONOMIA A LUZ PROVENIENTE DE ESTRELAS DISTANTES PROVA QUE O UNIVERSO É ANTIGO? Vivemos num universo
ASTRONOMIA A coisa mais incompreensível a respeito do Universo é que ele é compreensível Albert Einstein ASTRONOMIA A LUZ PROVENIENTE DE ESTRELAS DISTANTES PROVA QUE O UNIVERSO É ANTIGO? Vivemos num universo
Podemos encontrar uma figura interessante no PMBOK (Capítulo 7) sobre a necessidade de organizarmos o fluxo de caixa em um projeto.
 Discussão sobre Nivelamento Baseado em Fluxo de Caixa. Item aberto na lista E-Plan Podemos encontrar uma figura interessante no PMBOK (Capítulo 7) sobre a necessidade de organizarmos o fluxo de caixa em
Discussão sobre Nivelamento Baseado em Fluxo de Caixa. Item aberto na lista E-Plan Podemos encontrar uma figura interessante no PMBOK (Capítulo 7) sobre a necessidade de organizarmos o fluxo de caixa em
6 Conclusões e Trabalhos futuros 6.1. Conclusões
 6 Conclusões e Trabalhos futuros 6.1. Conclusões Neste trabalho estudou-se o comportamento do sistema que foi denominado pendulo planar com a adição de uma roda de reação na haste do pendulo composta de
6 Conclusões e Trabalhos futuros 6.1. Conclusões Neste trabalho estudou-se o comportamento do sistema que foi denominado pendulo planar com a adição de uma roda de reação na haste do pendulo composta de
www.enemdescomplicado.com.br
 Exercícios de Física Gravitação Universal 1-A lei da gravitação universal de Newton diz que: a) os corpos se atraem na razão inversa de suas massas e na razão direta do quadrado de suas distâncias. b)
Exercícios de Física Gravitação Universal 1-A lei da gravitação universal de Newton diz que: a) os corpos se atraem na razão inversa de suas massas e na razão direta do quadrado de suas distâncias. b)
Lógica Indutiva. Aula 4. Prof. André Martins
 Lógica Indutiva Aula 4 Prof. André Martins É uma bruxa? Lógica Clássica (Dedutiva) Na Lógica Clássica, determinamos a veracidade de proposições a partir de outras proposições que julgamos verdadeiras.
Lógica Indutiva Aula 4 Prof. André Martins É uma bruxa? Lógica Clássica (Dedutiva) Na Lógica Clássica, determinamos a veracidade de proposições a partir de outras proposições que julgamos verdadeiras.
Pesquisa com Professores de Escolas e com Alunos da Graduação em Matemática
 Pesquisa com Professores de Escolas e com Alunos da Graduação em Matemática Rene Baltazar Introdução Serão abordados, neste trabalho, significados e características de Professor Pesquisador e as conseqüências,
Pesquisa com Professores de Escolas e com Alunos da Graduação em Matemática Rene Baltazar Introdução Serão abordados, neste trabalho, significados e características de Professor Pesquisador e as conseqüências,
Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO)
 Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO) Parte: 1 Prof. Cristóvão Cunha Objetivos de aprendizagem
Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO) Parte: 1 Prof. Cristóvão Cunha Objetivos de aprendizagem
FUNÇÕES POLINOMIAIS DO SEGUNDO GRAU MEDIADOS PELO SOFTWARE GEOGEBRA NA PERSPECTIVA DOS REGISTROS DE REPRESENTAÇÃO SEMIÓTICA
 FUNÇÕES POLINOMIAIS DO SEGUNDO GRAU MEDIADOS PELO SOFTWARE GEOGEBRA NA PERSPECTIVA DOS REGISTROS DE REPRESENTAÇÃO SEMIÓTICA Modalidade: Relato de experiência Izaias Cordeiro Néri Mestrando em Educação
FUNÇÕES POLINOMIAIS DO SEGUNDO GRAU MEDIADOS PELO SOFTWARE GEOGEBRA NA PERSPECTIVA DOS REGISTROS DE REPRESENTAÇÃO SEMIÓTICA Modalidade: Relato de experiência Izaias Cordeiro Néri Mestrando em Educação
A origem dos filósofos e suas filosofias
 A Grécia e o nascimento da filosofia A origem dos filósofos e suas filosofias Você certamente já ouviu falar de algo chamado Filosofia. Talvez conheça alguém com fama de filósofo, ou quem sabe a expressão
A Grécia e o nascimento da filosofia A origem dos filósofos e suas filosofias Você certamente já ouviu falar de algo chamado Filosofia. Talvez conheça alguém com fama de filósofo, ou quem sabe a expressão
OBJETIVOS: CARGA HORÁRIA MÍNIMA CRONOGRAMA:
 ESTUDO DIRIGIDO COMPONENTE CURRICULAR: Controle de Processos e Instrumentação PROFESSOR: Dorival Rosa Brito ESTUDO DIRIGIDO: Métodos de Determinação de Parâmetros de Processos APRESENTAÇÃO: O rápido desenvolvimento
ESTUDO DIRIGIDO COMPONENTE CURRICULAR: Controle de Processos e Instrumentação PROFESSOR: Dorival Rosa Brito ESTUDO DIRIGIDO: Métodos de Determinação de Parâmetros de Processos APRESENTAÇÃO: O rápido desenvolvimento
Leonardo Cavalcante Daniel Santos Costa
 Leonardo Cavalcante Daniel Santos Costa Novatec capítulo 1 INTRODUÇÃO Provavelmente você, leitor, perderá dinheiro com o mercado financeiro. Isso mesmo. Repito: provavelmente perderá dinheiro com o mercado
Leonardo Cavalcante Daniel Santos Costa Novatec capítulo 1 INTRODUÇÃO Provavelmente você, leitor, perderá dinheiro com o mercado financeiro. Isso mesmo. Repito: provavelmente perderá dinheiro com o mercado
junho/june 2012 - Revista O Papel
 sérgio brito Por Luiz Bersou, diretor do Instituto Épico de Administração : luizbersou@bcaconsultoria.com.br Gestão por Ponto Flutuante H Gráfico 1 enry Ford, diz a história, propunha-se a fabricar carros
sérgio brito Por Luiz Bersou, diretor do Instituto Épico de Administração : luizbersou@bcaconsultoria.com.br Gestão por Ponto Flutuante H Gráfico 1 enry Ford, diz a história, propunha-se a fabricar carros
BC-0005 Bases Computacionais da Ciência. Modelagem e simulação
 BC-0005 Bases Computacionais da Ciência Aula 8 Modelagem e simulação Santo André, julho de 2010 Roteiro da Aula Modelagem O que é um modelo? Tipos de modelos Simulação O que é? Como pode ser feita? Exercício:
BC-0005 Bases Computacionais da Ciência Aula 8 Modelagem e simulação Santo André, julho de 2010 Roteiro da Aula Modelagem O que é um modelo? Tipos de modelos Simulação O que é? Como pode ser feita? Exercício:
Hoje estou elétrico!
 A U A UL LA Hoje estou elétrico! Ernesto, observado por Roberto, tinha acabado de construir um vetor com um pedaço de papel, um fio de meia, um canudo e um pedacinho de folha de alumínio. Enquanto testava
A U A UL LA Hoje estou elétrico! Ernesto, observado por Roberto, tinha acabado de construir um vetor com um pedaço de papel, um fio de meia, um canudo e um pedacinho de folha de alumínio. Enquanto testava
Correlação e Regressão Linear
 Correlação e Regressão Linear A medida de correlação é o tipo de medida que se usa quando se quer saber se duas variáveis possuem algum tipo de relação, de maneira que quando uma varia a outra varia também.
Correlação e Regressão Linear A medida de correlação é o tipo de medida que se usa quando se quer saber se duas variáveis possuem algum tipo de relação, de maneira que quando uma varia a outra varia também.
PROCESSO DE DESENVOLVIMENTO DE SOFTWARE. Modelos de Processo de Desenvolvimento de Software
 PROCESSO DE DESENVOLVIMENTO DE SOFTWARE Introdução Modelos de Processo de Desenvolvimento de Software Os modelos de processos de desenvolvimento de software surgiram pela necessidade de dar resposta às
PROCESSO DE DESENVOLVIMENTO DE SOFTWARE Introdução Modelos de Processo de Desenvolvimento de Software Os modelos de processos de desenvolvimento de software surgiram pela necessidade de dar resposta às
A MATEMÁTICA NO ENSINO SUPERIOR POLICIAL 1
 A MATEMÁTICA NO ENSINO SUPERIOR POLICIAL 1 A IMPORTÂNCIA DA MATEMÁTICA O desenvolvimento das sociedades tem sido também materializado por um progresso acentuado no plano científico e nos diversos domínios
A MATEMÁTICA NO ENSINO SUPERIOR POLICIAL 1 A IMPORTÂNCIA DA MATEMÁTICA O desenvolvimento das sociedades tem sido também materializado por um progresso acentuado no plano científico e nos diversos domínios
Introdução. 1.1 Histórico
 1 Introdução 1.1 Histórico O mercado brasileiro, assim como os mercados da maioria dos países emergentes, tem se caracterizado pela crescente volatilidade e dependência do capital estrangeiro. A integração
1 Introdução 1.1 Histórico O mercado brasileiro, assim como os mercados da maioria dos países emergentes, tem se caracterizado pela crescente volatilidade e dependência do capital estrangeiro. A integração
Lev Semenovich Vygotsky, nasce em 17 de novembro de 1896, na cidade de Orsha, em Bielarus. Morre em 11 de junho de 1934.
 Lev Semenovich Vygotsky, nasce em 17 de novembro de 1896, na cidade de Orsha, em Bielarus. Morre em 11 de junho de 1934. Lev Vygotsky, viveu na mesma época que Piaget (ambos nasceram em 1896 entanto Vygotsky
Lev Semenovich Vygotsky, nasce em 17 de novembro de 1896, na cidade de Orsha, em Bielarus. Morre em 11 de junho de 1934. Lev Vygotsky, viveu na mesma época que Piaget (ambos nasceram em 1896 entanto Vygotsky
CONSTRUINDO UMA PONTE TRELIÇADA DE PALITOS DE PICOLÉ
 CONSTRUINDO UMA PONTE TRELIÇADA DE PALITOS DE PICOLÉ Objetivo do projeto. Neste projeto, você irá construir um modelo de ponte treliçada que já estará previamente projetada. Quando terminada a etapa construção,
CONSTRUINDO UMA PONTE TRELIÇADA DE PALITOS DE PICOLÉ Objetivo do projeto. Neste projeto, você irá construir um modelo de ponte treliçada que já estará previamente projetada. Quando terminada a etapa construção,
Análises: Análise Fundamentalista Análise Técnica
 Análises: Análise Fundamentalista Análise Técnica Análise Fundamentalista Origem remonta do final do século XIX e princípio do século XX, quando as corretoras de bolsa tinham seus departamentos de análise
Análises: Análise Fundamentalista Análise Técnica Análise Fundamentalista Origem remonta do final do século XIX e princípio do século XX, quando as corretoras de bolsa tinham seus departamentos de análise
PARADOXO DA REALIZAÇÃO DE TRABALHO PELA FORÇA MAGNÉTICA
 PARADOXO DA REALIZAÇÃO DE TRABALHO PELA FORÇA MAGNÉTICA Marcelo da S. VIEIRA 1, Elder Eldervitch C. de OLIVEIRA 2, Pedro Carlos de Assis JÚNIOR 3,Christianne Vitor da SILVA 4, Félix Miguel de Oliveira
PARADOXO DA REALIZAÇÃO DE TRABALHO PELA FORÇA MAGNÉTICA Marcelo da S. VIEIRA 1, Elder Eldervitch C. de OLIVEIRA 2, Pedro Carlos de Assis JÚNIOR 3,Christianne Vitor da SILVA 4, Félix Miguel de Oliveira
Big Data marca início da Semana de Informática da Fema
 Big Data marca início da Semana de Informática da Fema Começou na segunda-feira, 23, a 24ª Semana de Informática da Fundação Educacional do Município de Assis Fema, evento promovido pela Coordenadoria
Big Data marca início da Semana de Informática da Fema Começou na segunda-feira, 23, a 24ª Semana de Informática da Fundação Educacional do Município de Assis Fema, evento promovido pela Coordenadoria
Análise e Resolução da prova de Auditor Fiscal da Fazenda Estadual do Piauí Disciplina: Matemática Financeira Professor: Custódio Nascimento
 Análise e Resolução da prova de Auditor Fiscal da Fazenda Estadual do Piauí Disciplina: Professor: Custódio Nascimento 1- Análise da prova Neste artigo, faremos a análise das questões de cobradas na prova
Análise e Resolução da prova de Auditor Fiscal da Fazenda Estadual do Piauí Disciplina: Professor: Custódio Nascimento 1- Análise da prova Neste artigo, faremos a análise das questões de cobradas na prova
Projeto de Sistemas I
 Instituto Federal de Educação, Ciência e Tecnologia de São Paulo Projeto de Sistemas I Professora: Kelly de Paula Cunha E-mail:kellypcsoares@ifsp.edu.br Requisitos: base para todo projeto, definindo o
Instituto Federal de Educação, Ciência e Tecnologia de São Paulo Projeto de Sistemas I Professora: Kelly de Paula Cunha E-mail:kellypcsoares@ifsp.edu.br Requisitos: base para todo projeto, definindo o
FATEC Cruzeiro José da Silva. Ferramenta CRM como estratégia de negócios
 FATEC Cruzeiro José da Silva Ferramenta CRM como estratégia de negócios Cruzeiro SP 2008 FATEC Cruzeiro José da Silva Ferramenta CRM como estratégia de negócios Projeto de trabalho de formatura como requisito
FATEC Cruzeiro José da Silva Ferramenta CRM como estratégia de negócios Cruzeiro SP 2008 FATEC Cruzeiro José da Silva Ferramenta CRM como estratégia de negócios Projeto de trabalho de formatura como requisito
Curso CPA-10 Certificação ANBID Módulo 4 - Princípios de Investimento
 Pág: 1/18 Curso CPA-10 Certificação ANBID Módulo 4 - Princípios de Investimento Pág: 2/18 Módulo 4 - Princípios de Investimento Neste módulo são apresentados os principais fatores para a análise de investimentos,
Pág: 1/18 Curso CPA-10 Certificação ANBID Módulo 4 - Princípios de Investimento Pág: 2/18 Módulo 4 - Princípios de Investimento Neste módulo são apresentados os principais fatores para a análise de investimentos,
UMA APLICAÇÃO DA MATEMÁTICA FINANCEIRA À TEORIA DO CAOS PARA OS ANOS FINAIS DO ENSINO FUNDAMENTAL
 UMA APLICAÇÃO DA MATEMÁTICA FINANCEIRA À TEORIA DO CAOS PARA OS ANOS FINAIS DO ENSINO FUNDAMENTAL Eliana Einsfeld Krindges Escola Barão do Rio Branco elianaeinsfeld@hotmail.com Janaína Poffo Escola Barão
UMA APLICAÇÃO DA MATEMÁTICA FINANCEIRA À TEORIA DO CAOS PARA OS ANOS FINAIS DO ENSINO FUNDAMENTAL Eliana Einsfeld Krindges Escola Barão do Rio Branco elianaeinsfeld@hotmail.com Janaína Poffo Escola Barão
Algoritmos. Objetivo principal: explicar que a mesma ação pode ser realizada de várias maneiras, e que às vezes umas são melhores que outras.
 6 6 NOME DA AULA: 6 Algoritmos Duração da aula: 45 60 minutos Tempo de preparação: 10-25 minutos (dependendo da disponibilidade de tangrans prontos ou da necessidade de cortá-los à mão) Objetivo principal:
6 6 NOME DA AULA: 6 Algoritmos Duração da aula: 45 60 minutos Tempo de preparação: 10-25 minutos (dependendo da disponibilidade de tangrans prontos ou da necessidade de cortá-los à mão) Objetivo principal:
Caracterização temporal de circuitos: análise de transientes e regime permanente. Condições iniciais e finais e resolução de exercícios.
 Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Sumário. Prefácio... xi. Prólogo A Física tira você do sério?... 1. Lei da Ação e Reação... 13
 Sumário Prefácio................................................................. xi Prólogo A Física tira você do sério?........................................... 1 1 Lei da Ação e Reação..................................................
Sumário Prefácio................................................................. xi Prólogo A Física tira você do sério?........................................... 1 1 Lei da Ação e Reação..................................................
TIPOS DE BRINCADEIRAS E COMO AJUDAR A CRIANÇA BRINCAR
 TIPOS DE BRINCADEIRAS E COMO AJUDAR A CRIANÇA BRINCAR As crianças precisam atravessar diversos estágios no aprendizado de brincar em conjunto, antes de serem capazes de aproveitar as brincadeiras de grupo.
TIPOS DE BRINCADEIRAS E COMO AJUDAR A CRIANÇA BRINCAR As crianças precisam atravessar diversos estágios no aprendizado de brincar em conjunto, antes de serem capazes de aproveitar as brincadeiras de grupo.
Protocolo em Rampa Manual de Referência Rápida
 Protocolo em Rampa Manual de Referência Rápida 1 O que é o Protocolo em Rampa O protocolo em rampa é um protocolo para testes de esforço que não possui estágios. Nele o incremento da carga se dá de maneira
Protocolo em Rampa Manual de Referência Rápida 1 O que é o Protocolo em Rampa O protocolo em rampa é um protocolo para testes de esforço que não possui estágios. Nele o incremento da carga se dá de maneira
Problemas insolúveis. Um exemplo simples e concreto
 Surge agora uma outra questão. Viemos buscando algoritmos para resolver problemas. No entanto, será que sempre seria possível achar esses algoritmos? Colocando de outra forma: será que, para todo problema,
Surge agora uma outra questão. Viemos buscando algoritmos para resolver problemas. No entanto, será que sempre seria possível achar esses algoritmos? Colocando de outra forma: será que, para todo problema,
Estudaremos aqui como essa transformação pode ser entendida a partir do teorema do trabalho-energia.
 ENERGIA POTENCIAL Uma outra forma comum de energia é a energia potencial U. Para falarmos de energia potencial, vamos pensar em dois exemplos: Um praticante de bungee-jump saltando de uma plataforma. O
ENERGIA POTENCIAL Uma outra forma comum de energia é a energia potencial U. Para falarmos de energia potencial, vamos pensar em dois exemplos: Um praticante de bungee-jump saltando de uma plataforma. O
ROTEIRO PARA ELABORAÇÃO DE PROJETOS
 APRESENTAÇÃO ROTEIRO PARA ELABORAÇÃO DE PROJETOS Breve histórico da instituição seguido de diagnóstico e indicadores sobre a temática abrangida pelo projeto, especialmente dados que permitam análise da
APRESENTAÇÃO ROTEIRO PARA ELABORAÇÃO DE PROJETOS Breve histórico da instituição seguido de diagnóstico e indicadores sobre a temática abrangida pelo projeto, especialmente dados que permitam análise da
Qual é o risco real do Private Equity?
 Opinião Qual é o risco real do Private Equity? POR IVAN HERGER, PH.D.* O debate nos mercados financeiros vem sendo dominado pela crise de crédito e alta volatilidade nos mercados acionários. Embora as
Opinião Qual é o risco real do Private Equity? POR IVAN HERGER, PH.D.* O debate nos mercados financeiros vem sendo dominado pela crise de crédito e alta volatilidade nos mercados acionários. Embora as
Universidade Federal de Minas Gerais ICEx / DCC
 Universidade Federal de Minas Gerais ICEx / DCC Belo Horizonte, 15 de dezembro de 2006 Relatório sobre aplicação de Mineração de Dados Mineração de Dados em Bases de Dados de Vestibulares da UFMG Professor:
Universidade Federal de Minas Gerais ICEx / DCC Belo Horizonte, 15 de dezembro de 2006 Relatório sobre aplicação de Mineração de Dados Mineração de Dados em Bases de Dados de Vestibulares da UFMG Professor:
1. Conceitos de sistemas. Conceitos da Teoria de Sistemas. Conceitos de sistemas extraídos do dicionário Aurélio:
 1. Conceitos de sistemas Conceitos da Teoria de Sistemas OPTNER: É um conjunto de objetos com um determinado conjunto de relações entre seus objetos e seus atributos. TILLES: É um conjunto de partes inter-relacionadas.
1. Conceitos de sistemas Conceitos da Teoria de Sistemas OPTNER: É um conjunto de objetos com um determinado conjunto de relações entre seus objetos e seus atributos. TILLES: É um conjunto de partes inter-relacionadas.
Estudo de funções parte 2
 Módulo 2 Unidade 13 Estudo de funções parte 2 Para início de conversa... Taxa de desemprego no Brasil cai a 5,8% em maio A taxa de desempregados no Brasil caiu para 5,8% em maio, depois de registrar 6%
Módulo 2 Unidade 13 Estudo de funções parte 2 Para início de conversa... Taxa de desemprego no Brasil cai a 5,8% em maio A taxa de desempregados no Brasil caiu para 5,8% em maio, depois de registrar 6%
1. Um corpo arremessado tem sua trajetória representada pelo gráfico de uma parábola, conforme a figura a seguir.
 1. Um corpo arremessado tem sua trajetória representada pelo gráfico de uma parábola, conforme a figura a seguir. Nessa trajetória, a altura máxima, em metros, atingida pelo corpo foi de a) 0,52m. b) 0,64m.
1. Um corpo arremessado tem sua trajetória representada pelo gráfico de uma parábola, conforme a figura a seguir. Nessa trajetória, a altura máxima, em metros, atingida pelo corpo foi de a) 0,52m. b) 0,64m.
Conceito de Contabilidade
 !" $%&!" #$ "!%!!&$$!!' %$ $(%& )* &%""$!+,%!%!& $+,&$ $(%'!%!-'"&!%%.+,&(+&$ /&$/+0!!$ & "!%!!&$$!!' % $ $(% &!)#$ %1$%, $! "# # #$ &&$ &$ 0&$ 01% & $ #$ % & #$&&$&$&* % %"!+,$%2 %"!31$%"%1%%+3!' #$ "
!" $%&!" #$ "!%!!&$$!!' %$ $(%& )* &%""$!+,%!%!& $+,&$ $(%'!%!-'"&!%%.+,&(+&$ /&$/+0!!$ & "!%!!&$$!!' % $ $(% &!)#$ %1$%, $! "# # #$ &&$ &$ 0&$ 01% & $ #$ % & #$&&$&$&* % %"!+,$%2 %"!31$%"%1%%+3!' #$ "
5 Equacionando os problemas
 A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
Leis de Newton. Dinâmica das partículas Física Aplicada http://www.walmorgodoi.com
 Leis de Newton Dinâmica das partículas Física Aplicada http://www.walmorgodoi.com Antes de Galileu Durante séculos, o estudo do movimento e suas causas tornou-se o tema central da filosofia natural. Antes
Leis de Newton Dinâmica das partículas Física Aplicada http://www.walmorgodoi.com Antes de Galileu Durante séculos, o estudo do movimento e suas causas tornou-se o tema central da filosofia natural. Antes
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica
 O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
TRABALHO DE ECONOMIA:
 UNIVERSIDADE DO ESTADO DE MINAS GERAIS - UEMG FUNDAÇÃO EDUCACIONAL DE ITUIUTABA - FEIT INSTITUTO SUPERIOR DE ENSINO E PESQUISA DE ITUIUTABA - ISEPI DIVINO EURÍPEDES GUIMARÃES DE OLIVEIRA TRABALHO DE ECONOMIA:
UNIVERSIDADE DO ESTADO DE MINAS GERAIS - UEMG FUNDAÇÃO EDUCACIONAL DE ITUIUTABA - FEIT INSTITUTO SUPERIOR DE ENSINO E PESQUISA DE ITUIUTABA - ISEPI DIVINO EURÍPEDES GUIMARÃES DE OLIVEIRA TRABALHO DE ECONOMIA:
)HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR
 6LPXODomR GH6LVWHPDV )HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR #5,6. Simulador voltado para análise de risco financeiro 3RQWRV IRUWHV Fácil de usar. Funciona integrado a ferramentas já bastante conhecidas,
6LPXODomR GH6LVWHPDV )HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR #5,6. Simulador voltado para análise de risco financeiro 3RQWRV IRUWHV Fácil de usar. Funciona integrado a ferramentas já bastante conhecidas,
A Sociologia de Weber
 Material de apoio para Monitoria 1. (UFU 2011) A questão do método nas ciências humanas (também denominadas ciências históricas, ciências sociais, ciências do espírito, ciências da cultura) foi objeto
Material de apoio para Monitoria 1. (UFU 2011) A questão do método nas ciências humanas (também denominadas ciências históricas, ciências sociais, ciências do espírito, ciências da cultura) foi objeto
O que é a ciência de dados (data science). Discussão do conceito. Luís Borges Gouveia Universidade Fernando Pessoa Versão 1.
 O que é a ciência de dados (data science). Discussão do conceito Luís Borges Gouveia Universidade Fernando Pessoa Versão 1.3, Outubro, 2015 Nota prévia Esta apresentação tem por objetivo, proporcionar
O que é a ciência de dados (data science). Discussão do conceito Luís Borges Gouveia Universidade Fernando Pessoa Versão 1.3, Outubro, 2015 Nota prévia Esta apresentação tem por objetivo, proporcionar
Resumo. Leonel Fonseca Ivo. 17 de novembro de 2009
 Resumo Leonel Fonseca Ivo 17 de novembro de 2009 1 Teoria de Sistemas A Teoria de Sistemas (TS) é um ramo específico da Teoria Geral de Sistemas (TGS), cujo objetivo é produzir teorias e formulações conceituais
Resumo Leonel Fonseca Ivo 17 de novembro de 2009 1 Teoria de Sistemas A Teoria de Sistemas (TS) é um ramo específico da Teoria Geral de Sistemas (TGS), cujo objetivo é produzir teorias e formulações conceituais
TEORIA GERAL DOS SISTEMAS
 TEORIA GERAL DOS SISTEMAS 2 HISTÓRICO Gottfried Leibniz (1646-1716) chamava de Sistema: Repertório de conhecimentos que não se limitasse a ser um simples inventário, mas que contivesse suas razões ou provas
TEORIA GERAL DOS SISTEMAS 2 HISTÓRICO Gottfried Leibniz (1646-1716) chamava de Sistema: Repertório de conhecimentos que não se limitasse a ser um simples inventário, mas que contivesse suas razões ou provas
TIPOS DE REFLEXÃO Regular Difusa
 Reflexão da luz TIPOS DE REFLEXÃO Regular Difusa LEIS DA REFLEXÃO RI = raio de luz incidente i normal r RR = raio de luz refletido i = ângulo de incidência (é formado entre RI e N) r = ângulo de reflexão
Reflexão da luz TIPOS DE REFLEXÃO Regular Difusa LEIS DA REFLEXÃO RI = raio de luz incidente i normal r RR = raio de luz refletido i = ângulo de incidência (é formado entre RI e N) r = ângulo de reflexão
INOVAÇÃO NA ADVOCACIA A ESTRATÉGIA DO OCEANO AZUL NOS ESCRITÓRIOS JURÍDICOS
 INOVAÇÃO NA ADVOCACIA A ESTRATÉGIA DO OCEANO AZUL NOS ESCRITÓRIOS JURÍDICOS Ari Lima Um empreendimento comercial tem duas e só duas funções básicas: marketing e inovação. O resto são custos. Peter Drucker
INOVAÇÃO NA ADVOCACIA A ESTRATÉGIA DO OCEANO AZUL NOS ESCRITÓRIOS JURÍDICOS Ari Lima Um empreendimento comercial tem duas e só duas funções básicas: marketing e inovação. O resto são custos. Peter Drucker
Disciplina: Introdução à Informática Profª Érica Barcelos
 Disciplina: Introdução à Informática Profª Érica Barcelos CAPÍTULO 4 1. ARQUITETURA DO COMPUTADOR- HARDWARE Todos os componentes físicos constituídos de circuitos eletrônicos interligados são chamados
Disciplina: Introdução à Informática Profª Érica Barcelos CAPÍTULO 4 1. ARQUITETURA DO COMPUTADOR- HARDWARE Todos os componentes físicos constituídos de circuitos eletrônicos interligados são chamados
15 O sistema solar e seus planetas
 A U A UL LA Atenção O sistema solar e seus planetas Leia com atenção as notícias abaixo, que apareceram em jornais de diferentes épocas. ANO DE 1781 CIENTISTAS DESCOBREM NOVO PLANETA De há quase 2.000
A U A UL LA Atenção O sistema solar e seus planetas Leia com atenção as notícias abaixo, que apareceram em jornais de diferentes épocas. ANO DE 1781 CIENTISTAS DESCOBREM NOVO PLANETA De há quase 2.000
Capítulo 4 Trabalho e Energia
 Capítulo 4 Trabalho e Energia Este tema é, sem dúvidas, um dos mais importantes na Física. Na realidade, nos estudos mais avançados da Física, todo ou quase todos os problemas podem ser resolvidos através
Capítulo 4 Trabalho e Energia Este tema é, sem dúvidas, um dos mais importantes na Física. Na realidade, nos estudos mais avançados da Física, todo ou quase todos os problemas podem ser resolvidos através
Súmula Teoria Energética. Paulo Gontijo
 Súmula Teoria Energética Paulo Gontijo O Universo Chama-se Universo ao conjunto de todas as coisas. Sua existência pressupõe a necessidade de dois conceitos anteriores a ele, que se denominam existência
Súmula Teoria Energética Paulo Gontijo O Universo Chama-se Universo ao conjunto de todas as coisas. Sua existência pressupõe a necessidade de dois conceitos anteriores a ele, que se denominam existência
4 Avaliação Econômica
 4 Avaliação Econômica Este capítulo tem o objetivo de descrever a segunda etapa da metodologia, correspondente a avaliação econômica das entidades de reservas. A avaliação econômica é realizada a partir
4 Avaliação Econômica Este capítulo tem o objetivo de descrever a segunda etapa da metodologia, correspondente a avaliação econômica das entidades de reservas. A avaliação econômica é realizada a partir
SERÁ NECESSÁRIA UMA FORÇA PARA
 Ano Lectivo 2010/2011 Professora Fátima Pires FÍSICO-QUÍMICA SERÁ NECESSÁRIA UMA FORÇA PARA QUE UM CORPO SE MOVA? Avaliação: Professora: Observações: 11ºB «Será necessária uma força para que um corpo se
Ano Lectivo 2010/2011 Professora Fátima Pires FÍSICO-QUÍMICA SERÁ NECESSÁRIA UMA FORÇA PARA QUE UM CORPO SE MOVA? Avaliação: Professora: Observações: 11ºB «Será necessária uma força para que um corpo se
um metro. A aceleração da gravidade na Lua é equivalente a um sexto da aceleração da gravidade da Terra.
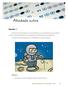 Atividade extra Questão 1 Durante uma viagem de pesquisa à Lua, um astronauta deixa cair um ovo na superfície da Lua,de uma altura de um metro. A aceleração da gravidade na Lua é equivalente a um sexto
Atividade extra Questão 1 Durante uma viagem de pesquisa à Lua, um astronauta deixa cair um ovo na superfície da Lua,de uma altura de um metro. A aceleração da gravidade na Lua é equivalente a um sexto
A ORGANIZAÇÃO DO TRABALHO PEDAGÓGICO COMO PRINCÍPIO EDUCATIVO NA FORMAÇÃO DE PROFESSORES
 A ORGANIZAÇÃO DO TRABALHO PEDAGÓGICO COMO PRINCÍPIO EDUCATIVO NA FORMAÇÃO DE Universidade Estadual De Maringá gasparin01@brturbo.com.br INTRODUÇÃO Ao pensarmos em nosso trabalho profissional, muitas vezes,
A ORGANIZAÇÃO DO TRABALHO PEDAGÓGICO COMO PRINCÍPIO EDUCATIVO NA FORMAÇÃO DE Universidade Estadual De Maringá gasparin01@brturbo.com.br INTRODUÇÃO Ao pensarmos em nosso trabalho profissional, muitas vezes,
Matemática Financeira II
 Módulo 3 Unidade 28 Matemática Financeira II Para início de conversa... Notícias como essas são encontradas em jornais com bastante frequência atualmente. Essas situações de aumentos e outras como financiamentos
Módulo 3 Unidade 28 Matemática Financeira II Para início de conversa... Notícias como essas são encontradas em jornais com bastante frequência atualmente. Essas situações de aumentos e outras como financiamentos
Estabilizada de. PdP. Autor: Luís Fernando Patsko Nível: Intermediário Criação: 22/02/2006 Última versão: 18/12/2006
 TUTORIAL Fonte Estabilizada de 5 Volts Autor: Luís Fernando Patsko Nível: Intermediário Criação: 22/02/2006 Última versão: 18/12/2006 PdP Pesquisa e Desenvolvimento de Produtos http://www.maxwellbohr.com.br
TUTORIAL Fonte Estabilizada de 5 Volts Autor: Luís Fernando Patsko Nível: Intermediário Criação: 22/02/2006 Última versão: 18/12/2006 PdP Pesquisa e Desenvolvimento de Produtos http://www.maxwellbohr.com.br
Capítulo 15: Investimento, Tempo e Mercado de Capitais
 Pindyck & Rubinfeld, Capítulo 15, Mercado de Capitais :: EXERCÍCIOS 1. Suponha que a taxa de juro seja de 10%. Qual é o valor de um título com cupom que paga $80 por ano, durante cada um dos próximos 5
Pindyck & Rubinfeld, Capítulo 15, Mercado de Capitais :: EXERCÍCIOS 1. Suponha que a taxa de juro seja de 10%. Qual é o valor de um título com cupom que paga $80 por ano, durante cada um dos próximos 5
MAT1154 ANÁLISE QUALITATIVA DE PONTOS DE EQUILÍBRIO DE SISTEMAS NÃO-LINEARES
 MAT1154 ANÁLISE QUALITATIVA DE PONTOS DE EQUILÍBRIO DE SISTEMAS NÃO-LINEARES VERSÃO 1.0.2 Resumo. Este texto resume e complementa alguns assuntos dos Capítulo 9 do Boyce DiPrima. 1. Sistemas autônomos
MAT1154 ANÁLISE QUALITATIVA DE PONTOS DE EQUILÍBRIO DE SISTEMAS NÃO-LINEARES VERSÃO 1.0.2 Resumo. Este texto resume e complementa alguns assuntos dos Capítulo 9 do Boyce DiPrima. 1. Sistemas autônomos
Avanços na transparência
 Avanços na transparência A Capes está avançando não apenas na questão dos indicadores, como vimos nas semanas anteriores, mas também na transparência do sistema. Este assunto será explicado aqui, com ênfase
Avanços na transparência A Capes está avançando não apenas na questão dos indicadores, como vimos nas semanas anteriores, mas também na transparência do sistema. Este assunto será explicado aqui, com ênfase
MARKETING DE RELACIONAMENTO UMA FERRAMENTA PARA AS INSTITUIÇÕES DE ENSINO SUPERIOR: ESTUDO SOBRE PORTAL INSTITUCIONAL
 MARKETING DE RELACIONAMENTO UMA FERRAMENTA PARA AS INSTITUIÇÕES DE ENSINO SUPERIOR: ESTUDO SOBRE PORTAL INSTITUCIONAL Prof. Dr. José Alberto Carvalho dos Santos Claro Mestrado em Gestão de Negócios Universidade
MARKETING DE RELACIONAMENTO UMA FERRAMENTA PARA AS INSTITUIÇÕES DE ENSINO SUPERIOR: ESTUDO SOBRE PORTAL INSTITUCIONAL Prof. Dr. José Alberto Carvalho dos Santos Claro Mestrado em Gestão de Negócios Universidade
Projeto CONDIGITAL Portas da Matemática Guia do Professor
 Projeto CONDIGITAL Portas da Matemática Guia do Professor Página 1 de 7 Caro(a) professor(a) Guia do Professor A utilização de simulações digitais como objetos de aprendizagem tem sido difundida atualmente
Projeto CONDIGITAL Portas da Matemática Guia do Professor Página 1 de 7 Caro(a) professor(a) Guia do Professor A utilização de simulações digitais como objetos de aprendizagem tem sido difundida atualmente
CAIXA ECONOMICA FEDERAL
 JUROS SIMPLES Juros Simples comercial é uma modalidade de juro calculado em relação ao capital inicial, neste modelo de capitalização, os juros de todos os períodos serão sempre iguais, pois eles serão
JUROS SIMPLES Juros Simples comercial é uma modalidade de juro calculado em relação ao capital inicial, neste modelo de capitalização, os juros de todos os períodos serão sempre iguais, pois eles serão
GESTÃO DA DIRETORIA DE MARKETING ATRAVÉS DE UMA DIVISÃO ESTRATÉGICA: OTIMIZANDO PROCESSOS E CAPACITANDO PESSOAS PRÁTICA INTERNA. Temática: Marketing
 GESTÃO DA DIRETORIA DE MARKETING ATRAVÉS DE UMA DIVISÃO ESTRATÉGICA: OTIMIZANDO PROCESSOS E CAPACITANDO PESSOAS PRÁTICA INTERNA Temática: Marketing Resumo: Identificada a sobrecarga de atividades na diretoria
GESTÃO DA DIRETORIA DE MARKETING ATRAVÉS DE UMA DIVISÃO ESTRATÉGICA: OTIMIZANDO PROCESSOS E CAPACITANDO PESSOAS PRÁTICA INTERNA Temática: Marketing Resumo: Identificada a sobrecarga de atividades na diretoria
Algoritmos e Programação (Prática) Profa. Andreza Leite andreza.leite@univasf.edu.br
 (Prática) Profa. Andreza Leite andreza.leite@univasf.edu.br Introdução O computador como ferramenta indispensável: Faz parte das nossas vidas; Por si só não faz nada de útil; Grande capacidade de resolução
(Prática) Profa. Andreza Leite andreza.leite@univasf.edu.br Introdução O computador como ferramenta indispensável: Faz parte das nossas vidas; Por si só não faz nada de útil; Grande capacidade de resolução
No mundo atual, globalizado e competitivo, as organizações têm buscado cada vez mais, meios de se destacar no mercado. Uma estratégia para o
 DATABASE MARKETING No mundo atual, globalizado e competitivo, as organizações têm buscado cada vez mais, meios de se destacar no mercado. Uma estratégia para o empresário obter sucesso em seu negócio é
DATABASE MARKETING No mundo atual, globalizado e competitivo, as organizações têm buscado cada vez mais, meios de se destacar no mercado. Uma estratégia para o empresário obter sucesso em seu negócio é
Indústria de Transformação Cearense em 2013: Algumas Evidências para os Resultados Acumulados até o Terceiro Trimestre
 Enfoque Econômico é uma publicação do IPECE que tem por objetivo fornecer informações de forma imediata sobre políticas econômicas, estudos e pesquisas de interesse da população cearense. Por esse instrumento
Enfoque Econômico é uma publicação do IPECE que tem por objetivo fornecer informações de forma imediata sobre políticas econômicas, estudos e pesquisas de interesse da população cearense. Por esse instrumento
SISTEMAS DE INFORMAÇÃO PARA GESTÃO
 07-05-2013 1 SISTEMAS DE INFORMAÇÃO PARA GESTÃO Aula I Docente: Eng. Hercílio Duarte 07-05-2013 2 Objectivo Sistemas Modelos Dados Vs. Informação Introdução aos sistemas de Informação 07-05-2013 3 Introdução
07-05-2013 1 SISTEMAS DE INFORMAÇÃO PARA GESTÃO Aula I Docente: Eng. Hercílio Duarte 07-05-2013 2 Objectivo Sistemas Modelos Dados Vs. Informação Introdução aos sistemas de Informação 07-05-2013 3 Introdução
Ponto de vista. Metodologia para um índice de confiança. E expectativas das seguradoras no Brasil
 Ponto de vista 40 Metodologia para um índice de confiança E expectativas das seguradoras no Brasil Francisco Galiza Em 2012, no Brasil, algumas previsões econômicas não fizeram muito sucesso. Por exemplo,
Ponto de vista 40 Metodologia para um índice de confiança E expectativas das seguradoras no Brasil Francisco Galiza Em 2012, no Brasil, algumas previsões econômicas não fizeram muito sucesso. Por exemplo,
CAPITAL DE GIRO: ESSÊNCIA DA VIDA EMPRESARIAL
 CAPITAL DE GIRO: ESSÊNCIA DA VIDA EMPRESARIAL Renara Tavares da Silva* RESUMO: Trata-se de maneira ampla da vitalidade da empresa fazer referência ao Capital de Giro, pois é através deste que a mesma pode
CAPITAL DE GIRO: ESSÊNCIA DA VIDA EMPRESARIAL Renara Tavares da Silva* RESUMO: Trata-se de maneira ampla da vitalidade da empresa fazer referência ao Capital de Giro, pois é através deste que a mesma pode
Apostila de Fundamentos de Programação I. Prof.: André Luiz Montevecchi
 Apostila de Fundamentos de Programação I Prof: André Luiz Montevecchi Introdução O mundo atual é dependente da tecnologia O uso intenso de diversos aparatos tecnológicos é parte integrante do nosso dia-a-dia
Apostila de Fundamentos de Programação I Prof: André Luiz Montevecchi Introdução O mundo atual é dependente da tecnologia O uso intenso de diversos aparatos tecnológicos é parte integrante do nosso dia-a-dia
Opções Reais. Processos Estocásticos. Processos Estocásticos. Modelando Incerteza. Processos Estocásticos
 Modelando Incerteza Opções Reais A incerteza em um projeto pode ter mais do que apenas dois estados. Na prática, o número de incertezas pode ser infinito Prof. Luiz Brandão brandao@iag.puc-rio.br IAG PUC-Rio
Modelando Incerteza Opções Reais A incerteza em um projeto pode ter mais do que apenas dois estados. Na prática, o número de incertezas pode ser infinito Prof. Luiz Brandão brandao@iag.puc-rio.br IAG PUC-Rio
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
 Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
EXERCÍCIO: R: 12.000 / 12,00 = 1.000 quotas
 1- Um senhor resolveu investir num Fundo de investimento, informou-se sobre o valor da ação e entregou seu dinheiro sob responsabilidade da administração do fundo. Ele tinha R$ 12.000,00 e o valor da ação
1- Um senhor resolveu investir num Fundo de investimento, informou-se sobre o valor da ação e entregou seu dinheiro sob responsabilidade da administração do fundo. Ele tinha R$ 12.000,00 e o valor da ação
ASSESSORIA DE IMPRENSA 1 Felipe Plá Bastos 2
 ASSESSORIA DE IMPRENSA 1 Felipe Plá Bastos 2 RESUMO: O presente trabalho tem como objetivo saber como é desenvolvido o trabalho de Assessoria de Imprensa, sendo um meio dentro da comunicação que através
ASSESSORIA DE IMPRENSA 1 Felipe Plá Bastos 2 RESUMO: O presente trabalho tem como objetivo saber como é desenvolvido o trabalho de Assessoria de Imprensa, sendo um meio dentro da comunicação que através
Pisa 2012: O que os dados dizem sobre o Brasil
 Pisa 2012: O que os dados dizem sobre o Brasil A OCDE (Organização para Cooperação e Desenvolvimento Econômico) divulgou nesta terça-feira os resultados do Programa Internacional de Avaliação de Alunos,
Pisa 2012: O que os dados dizem sobre o Brasil A OCDE (Organização para Cooperação e Desenvolvimento Econômico) divulgou nesta terça-feira os resultados do Programa Internacional de Avaliação de Alunos,
Filtros de sinais. Conhecendo os filtros de sinais.
 Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Orientação a Objetos
 1. Domínio e Aplicação Orientação a Objetos Um domínio é composto pelas entidades, informações e processos relacionados a um determinado contexto. Uma aplicação pode ser desenvolvida para automatizar ou
1. Domínio e Aplicação Orientação a Objetos Um domínio é composto pelas entidades, informações e processos relacionados a um determinado contexto. Uma aplicação pode ser desenvolvida para automatizar ou
DURATION - AVALIANDO O RISCO DE MUDANÇA NAS TAXAS DE JUROS PARTE ll
 DURATION - AVALIANDO O RISCO DE MUDANÇA NAS TAXAS DE JUROS PARTE ll! Qual a origem do conceito de duração?! Como calcular a duração?! Quais as limitações do cálculo da duração?! Como estimar a variação
DURATION - AVALIANDO O RISCO DE MUDANÇA NAS TAXAS DE JUROS PARTE ll! Qual a origem do conceito de duração?! Como calcular a duração?! Quais as limitações do cálculo da duração?! Como estimar a variação
Simulação Computacional de Sistemas, ou simplesmente Simulação
 Simulação Computacional de Sistemas, ou simplesmente Simulação Utilização de métodos matemáticos & estatísticos em programas computacionais visando imitar o comportamento de algum processo do mundo real.
Simulação Computacional de Sistemas, ou simplesmente Simulação Utilização de métodos matemáticos & estatísticos em programas computacionais visando imitar o comportamento de algum processo do mundo real.
XIX CONGRESSO DE PÓS-GRADUAÇÃO DA UFLA 27 de setembro a 01 de outubro de 2010
 OTIMIZAÇÃO DA EFETIVIDADE DE HEDGE NA COMPRA DE MILHO POR MEIO DE CONTRATOS FUTUROS PARA PRODUÇÃO DE BOVINOS DE CORTE RESUMO GUSTAVO DE SOUZA CAMPOS BADARÓ 1, RENATO ELIAS FONTES 2 ; TARCISIO GONÇALVES
OTIMIZAÇÃO DA EFETIVIDADE DE HEDGE NA COMPRA DE MILHO POR MEIO DE CONTRATOS FUTUROS PARA PRODUÇÃO DE BOVINOS DE CORTE RESUMO GUSTAVO DE SOUZA CAMPOS BADARÓ 1, RENATO ELIAS FONTES 2 ; TARCISIO GONÇALVES
