Controle Robusto Multivariável para um Veículo Submersível Autônomo ϑ Multivariable Robust Control for an Autonomous Underwater Vehicle
|
|
|
- Martim Franco Alencastre
- 8 Há anos
- Visualizações:
Transcrição
1 Controle Robusto Multivariável para um Veículo Submersível Autônomo ϑ Multivariable Robust Control for an Autonomous Underwater Vehicle Juan Carlos Cutipa Luque Decio Crisol Donha Departamento de Engenharia Mecânica - EPUSP. Av. Prof. Mello Moraes 223, CEP São Paulo, SP - Brasil Resumo. Este trabalho trata do controle dos movimentos de um Veículo Submersível Autônomo (VSA). Veículos submersíveis são difíceis de controlar devido à alta não linearidade de seus modelos, ao forte acoplamento de movimentos, ao desconhecimento de certas dinâmicas, às incertezas do próprio modelo, perturbações e devido ao ruído de sensores. A dificuldade de controle pode ser exacerbada quando o veículo é sub-atuado. Para realização deste trabalho foi escolhido um VSA do tipo torpedo, considerandose seis graus de liberdade (GL). A técnica da sensibilidade mista H foi usada, obtendo controladores centralizados capazes de superar o problema do forte acoplamento de movimentos. Nesta abordagem, formatam-se algumas funções de malha fechada ligadas a sensibilidade do sistema buscando garantir estabilidade e desempenho robustos. Os controladores desenvolvidos foram testados em simulações numéricas, produzindo uma grande quantidade de resultados. A análise destes resultados revela o poder e a flexibilidade das técnicas implementadas. Palavras-chaves: Controle Robusto Multivariável, Veículos Submersíveis Autônomos, Sensibilidade Mista H Abstract. This paper focuses the motion control of an Autonomous Underwater Vehicle (AUV). Underwater vehicles are difficult to control due to high non-linearities of its model, coupling between dynamics, unknown dynamics, model uncertainties, disturbances and sensor noises. Difficulty is greater, when the system is subactuated. In this work, a torpedo-like AUV was chosen, considering six degree of freedom (DOF). A H mixed sensitivity approach was used in the syntheses stage, leading to a centralized controller able to deal with all difficulties appointed above. This control approach is based on the shapping of well known closed-loop sensitivity functions, seeking to achieve stability and performance robustness. The controller developed where tested in a number of numerical simulations. Analyses of results reveals the power and flexibility of the implemented techniques. Keywords: Multivariable Robust Control, Autônomos Underwater Vehicles, H Mixed Sensitivity. Introdução Atividades submarinas para a exploração de recursos marinhos, pesquisas biológicas e aspectos relativos à segurança nacional dos países têm levado ao estudo e ao desenvolvimento de diversos tipos de veículos submersíveis de pequeno porte. O potencial tecnológico e econômico dos veículos submersíveis autônomos é apreciável, principalmente, em atividades como busca e prospecção de petróleo e gás natural em águas profundas, coleta de dados para pesquisas relacionadas ao meio-ambiente e à biologia marinha, inspeção de grandes estruturas flutuantes ou subaquáticas além da atuação em missões militares. Muitos trabalhos vêm sendo desenvolvidos para o controle destes veículos. Aplicações na indústria usam técnicas de controle clássico pela sintonia fácil dos parâmetros do controlador. Outras alternativas utilizam controladores de movimento de forma desacoplada (MCEWEN, 22; SILVESTRE; PASCOAL, 2). Porém, no ambiente marinho real, estão presentes distúrbios em forma de ondas e correntezas. Estes distúrbios, além dos ruídos dos sensores de navegação e incertezas do modelo, deterioram a estabilidade e o desempenho do sistema. Portanto, é necessário projetar um Controlador Robusto que garanta especificações de estabilidade ϑ Artigo extraído da dissertação: "Controle Robusto Multivariável para um Veículo Submersível Autônomo", de Juan C. C. Luque, apresentada à Escola Politécnica da Universidade de São Paulo sob a orientação do Prof. Dr. Decio Crisol Donha.
2 e desempenho, mesmo em condições muito adversas. No que se refere à aplicação de Controle Robusto em veículos submersíveis podem-se destacar trabalhos como os de Silvestre e Pascoal (2) e Whitcomb (2). Nestes trabalhos, a dinâmica do submersível é dividida em subsistemas de ordem reduzida. Um projeto de controle que envolve a dinâmica completa do modelo demandaria naturalmente maior esforço. (LOGAN, 993) contribuiu significativamente na aplicação de Controle Robusto para VSAs ao fazer a comparação entre duas técnicas muito bem conhecidas, o Controle H e o Controle por Modos Deslizantes (Sliding Mode), concluindo que ambas técnicas demandam muito esforço em sistemas multivariáveis, com forte acoplamento, porém os modos deslizantes seriam mais simples de se projetar para sistemas escalares. Entre os trabalhos de Controle Robusto que seguem a linha de modos deslizantes encontram-se Healey e Lienard (993), Song, An e Smith (22) e Souza (23). O objetivo deste trabalho é projetar um Controlador Robusto Multivariável centralizado para controlar os seis graus de liberdade de um veículo submersível autônomo, garantindo especificações de estabilidade e desempenho robustos, apesar de distúrbios de correntezas, ruídos nos sensores e as incertezas de modelagem. A metodologia a usar é a técnica de sensibilidade mista H. Este trabalho está organizado da seguinte forma: inicialmente apresentam-se as principais características do veículo, desde as suas dimensões até a representação do modelo dinâmico do veículo. Em seguida, é exposta a metodologia de Controle Robusto. Após as simulações feitas, mostram-se os resultados mais relevantes que levam à conclusão do trabalho. 2. Características e Modelo Dinâmico do VSA Nesta seção descreve-se o modelo matemático do VSA. Primeiramente, descrevem-se as características principais do veículo. O VSA tem a forma de charuto, com um comprimento total de,99 metros, um diâmetro de,624 metros e um deslocamento submerso de 4N. É movimentado pela ação de um propulsor e dois lemes para manobras de guinada e submersão. A variação do ângulo do leme vertical (δ r ) permite a realização de manobras de guinada e a variação do ângulo do leme horizontal (δ s ) permite a realização de manobras de submersão. O modelo não linear do veículo submersível está bem exposto em Donha e Luque (26), com seis equações da hidrodinâmica do submersível e seis equações de transformação de coordenadas. A figura mostra os dois referenciais usados nesta modelagem, o referencial fixo e o referencial móvel, define a nomenclatura e os símbolos utilizados. A figura 2 mostra a movimentação dos lemes. Todos os valores numéricos dos coeficientes hidrodinâmicos do modelo não linear estão em Canhetti (998). Vista Superior x δ r Vista Lateral δ s y z x v u ψ R. fixo u θ R. fixo Figura. Sistema de Coordenadas Figura 2. Movimento dos lemes w O modelo não linear do VSA foi linearizado usando a expansão em Séries de Taylor. O ponto de linearização escolhido foi na velocidade de cruzeiro do submersível (u=2m/s), o que levou a expressar o modelo linear para o veículo submersível autônomo: ẋ(t) = Ax(t) + Bu(t), x(t o ) = x o y(t) = Cx(t) + Du(t) Onde A é a matriz de estados de dimensão (8 8), B é a matriz de controle de dimensão (8 2), C é a matriz do observador de dimensão (4 8) e a matriz D, de dimensão (4 4). x(t) é o vetor de estados, u(t) é o vetor de entradas, y(t) é o vetor de observações, e x(t o ) é a condição inicial do sistema. A seguir descrevem-se cada um destes elementos. () Os valores numéricos estão no anexo. 2
3 vetor de estados: u m/s veloc. de avanço v m/s veloc. de deriva w m/s veloc. de arfagem x = p rad/s veloc. de q rad/s veloc. de r rad/s veloc. de guinada φ rad ângulo de θ rad ângulo de (2) vetor de entradas: [ ] δr rad leme horizontal u = δ s rad leme vertical vetor de observações: φ rad ângulo de y = θ rad ângulo de ψ rad/s veloc. de guinada (4) ż m/s veloc. de submersão A figura 3 mostra o sistema Linear Invariante no Tempo (LIT) acoplado resultante, onde as entradas são os lemes, vertical e horizontal, respectivamente. As variáveis observadas são:,, velocidade de guinada e velocidade de submersão. Um controlador PID simples foi projetado para garantir a velocidade de avanço constante (u=2m/s) em regime permanente. (3) Figura 3. Modelo linear do VSA. Para facilitar o projeto do controlador, as entradas do controlador são normalizadas considerando a saturação física dos atuadores: 3 para o leme vertical (δ r ) e 2 para o leme horizontal (δ s ). De acordo com Logan (993), também devem ser normalizadas considerando o máximo erro de acompanhamento do sinal de referência: para os ângulos de (φ) e (θ), /s para a velocidade de guinada ( ψ), e m/s para a velocidade de submersão (ż). Assume-se também que o máximo valor esperado do erro para as velocidade de avanço (u), deriva (v) e arfagem (w) é de m/s, o erro máximo para as velocidades angulares de (p), (q) e guinada (r) é de /s. Em seguida, obtém-se as matrizes para o modelo linear normalizado: A = S x.a.s x B = S x.b.s u C = S y.c.s x D = S y.d.s u () Após a normalização, o modelo em espaço de estados, usado no projeto do controlador, é expressado como segue (DONHA, 23): ẋ(t) = Ax(t) + B w(t) + B 2 u(t), x(t o ) = x o (6) z(t) = C x(t) + D w(t) + D 2 u(t) y(t) = C 2 x(t) + D 2 w(t) + D 22 u(t) onde x(.) é o vetor de estados, x(t o ) é o vetor da condição inicial do sistema, t é o tempo; u(.) é o vetor de entrada, w(.) é o vetor de distúrbio, z(.) é o vetor de controle e y(.) é o vetor de estados observados. 3. Síntese do Controlador A estratégia usual em sistemas de controle moderno para caracterizar os objetivos de desempenho é medir certas matrizes de transferência em malha fechada usando diversas normas de matrizes (SKOGESTAD; POSTLETHWAITE, 996). Essas normas estabelecem uma medida da magnitude dos sinais de saída que 3
4 podem-se obter a partir dos sinais de entrada, que é uma medida do ganho em sistemas. A norma H é uma norma muito conveniente para medir a matriz de transferência em malha fechada, e é definida por: N zω = sup = σ(n zω (jω)) (7) ω R onde σ(n zω (jω) é o supremo do valor singular máximo de N zω em todo o domínio ω. Existem muitas maneiras de formular o problema de controle e consequêntemente a seleção de funções de ponderação relacionadas com as especificações de desempenho (DONHA; KATEBI, 24). Um das estratégias mais usadas é a Sensibilidade Mista, que consiste na limitação de certas funções de ponderação, tal como: a sensibilidade do sistema S(s) = (I + GK(s)), a sensibilidade do controlador C(s) = KS(s) ou a sensibilidade complementar do sistema T (s) = I S(s). A figura 4 ilustra a representação padrão de dois portos, configuração usada na síntese do controlador, onde G é a planta nominal do veículo, K é o controlador, W são as funções de ponderação, r é o vetor de referência, di é o vetor de distúrbios de entrada, d é o vetor de distúrbios de saída, e ñ é o vetor de ruídos do sensor. N zw é a matriz de transferência de malha fechada com o controlador entre w e z, onde [ ] T [ẽ ] T w = r di d ñ é o vetor de entradas exógenas do sistema, e z = ũ ỹ é o vetor de saídas do sistema. O primeiro passo para a síntese do controlador H consiste em minimizar o índice de desempenho: neste caso formulado como segue: W S S N zw = W C C < γ (8) W T T onde γ é um numero real associado ao problema de controle ótimo. A ponderação W S feita sobre S(s) determinará o bom acompanhamento do sinal de referência e a atenuação dos distúrbios, a ponderação W C feita sobre C(s) limitará a ação do controle em alta freqüência, a ponderação W T sobre T limitará a banda passante do sistema em malha fechada e impõe um decaimento (roll off ) adequado a T (s). Assumindo que as matrizes envolvidas satisfazem as condições de detectabilidade e estabilizabilidade (ZHOU; DOYLE; GLOVER, 99), existe um controlador ótimo K(s) que satisfaz: N zw γ, dado por Skogestad e Postlethwaite (996): [ ] A Z K c (s) = L F (9) () onde: F = B T 2 X, L = Y C T 2, Z = (I γ 2 Y X ), () A = A + γ 2 B B T X + B 2 F + Z L C 2, (2) X e Y são soluções das equações algébricas de Ricatti, respectivamente ao problema de controle e ao problema de estimação. O segundo passo do controle H consiste na busca de parâmetros das diversas funções de ponderação (ZHOU; DOYLE; GLOVER, 99; SKOGESTAD; POSTLETHWAITE, 996). 3. Controlador de dois graus de liberdade (2-GL) É comum observar em sistemas multivariáveis com grande número de graus de liberdade, que as especificações de desempenho como rejeição de distúrbios e bom tracking não sejam atingidas simultaneamente com total sucesso (DONHA; LUQUE, 26). Portanto, outras estruturas devem ser investigadas para minimizar ou eliminar estes problemas, principalmente no caso de sistema sub-atuados, como é o caso em este estudo. A figura mostra uma estrutura alternativa, onde K é um controlador de dois graus de liberdade (2-GL) com a seguinte estrutura K = [K y K y ] T. A vantagem em usar um controlador 2-GL, também usado por Lundström, Skogestad e Doyle (999), é melhorar o tracking e as especificações da resposta temporal do 4
5 Planta Generalizada r d i d R W i W d r Planta Generalizada d e - W s W C W T e u y r d i d R W i W d r Wmodel d e - W s W C W T e u y n u W n n d i u d G y v - y P n u W n n d i u d G y v y P K K r Figura 4. Estrutura para síntese do controlador, -GL Figura. Estrutura para síntese do controlador, 2-GL sistema. O prefiltro K r é destinado à atingir as especificações no regime temporal, enquanto K y garante a estabilidade do sistema. E eventualmente, pode-se forçar o atendimento de especificações em freqüência através de W model, ajustando-o a um sistema de segunda ordem. Após estas modificações, o procedimento da síntese do controlador 2-GL segue os mesmos passos da síntese do controlador de um grau de liberdade antes descrito. Especificações de projeto As especificações do projeto são sumarizadas nos seguintes itens: E Estabilidade em malha fechada E2 σ(s) < para ω <, 7rad/s E3 σ(t ) < para ω > 2rad/s E4 σ(c) < para ω > 7rad/s E resposta temporal ao degrau Tabela. Resposta do sistema, assumindo um tempo de acomodação T = 4τ Sinal Ultrapassagem Tempo de /τ controlado percentual assentamento 2% 2s,2 % 2s,2 veloc. de guinada % 2s,2 veloc. de submersão % 8s, 3.2 Guiagem do VSA O sistema de guiagem é encarregado de guiar o veículo até um alvo ou acompanhar uma trajetória desejada, utilizando para este propósito a leitura das variáveis (x, y e z) e transformações cinemáticas, gerando o sinal de comando para as variáveis a serem controladas. O Controlador Robusto aciona as superfícies de controle (lemes), a partir dos sinais observados no sistema. A velocidade de avanço deve permanecer constate (2 m/s) em todo o trajeto. De acordo com a figura 6, duas variáveis são necessárias para conseguir movimentar o veículo no espaço 3D submarino: a velocidade de guinada e a velocidade de submersão. No movimento planar, a missão do veículo é acompanhar uma determinada trajetória, construída a partir de alvos desejados representados pelo par [x d (k), y d (k)], onde k =, 2,..., N definem a linha de visão ou LOS (Line of Sight) para a guinada (HEALEY; LIENARD, 993). Pode-se usar essa mesma estratégia, neste caso particular, para obter o sinal de mando da velocidade de guinada, como segue: ψ d (t) = d dt {ψ d(t)} (3)
6 onde, ( ) ψ d (t) = tan yd (k) y(t). (4) x d (k) x(t) Através da velocidade de guinada ( ψ d ) e da velocidade de submersão ż é possível manobrar o VSA no espaço tridimensional submarino. x,y,z desejado x,y,z Guiagem veloc. de guinada veloc. de submersão Controlador 2-GL veloc. de guinada veloc. de submersão mov. dos lemes VSA 6-GL Navegação Figura 6. Guiagem e Controle para o VSA. 4. Resultados Primeiramente, procede-se à validação do modelo linear para viabilizar a utilização da metodologia H no desenvolvimento do Controlador Robusto. Em seguida, são desenvolvidos dois controladores centralizados capazes de controlar o sistema dinâmico não linear do VSA. Faz-se a análise nos domínios de freqüência e tempo. A partir do controlador 2-GL implementada-se a guiagem do veículo. 4. Análise do Modelo Linear do VSA O modelo linear foi desenvolvido por linearização ao redor da velocidade de avanço (u = 2 m/s). O modelo linear é expresso pelas matrizes A, B, C e D, de onde pode-se avaliar as características dinâmicas do veículo submersível como: o acoplamento entre suas dinâmicas, resposta em freqüência, oscilações e instabilidade. Tabela 2. Pólos do Sistema Linear Invariante no Tempo Descrição Pólos arfagem/ (oscilação), 429±, 3i, 3, 4, 4 (oscilação), 36±, 98i, 98 deriva/ (oscilação), 9±, 322i, 343 velocidade de avanço, 324, 324 Os pólos do sistema não controlado de dimensão 8 são dados na tabela 2, observa-se que o modelo linear desenvolvido para o VSA é instável. Na figura 7 são ilustradas as magnitudes dos autovetores relativamente ao acoplamento dinâmico do sistema. Pode-se observar o forte acoplamento entre os movimentos de arfagem/ (figura 7(a)), deriva/ (figura 7(b)). O acoplamento deriva/ é freqüente em veículos marítimos através das variáveis (φ e ψ), por isso sistemas mais complexos usam técnicas de estabilização de (roll stabilization) para contrapor este efeito, (FOSSEN, 994). A possível causa de instabilidade do movimento de é associada ao momento de Munk. O momento de Munk tende a desestabilizar o veículo, colocando-o na direção perpendicular em relação ao fluxo, a razão é a localização assimétrica dos pontos de estagnação (TRIANTAFYLLOU; HOVER, 23). A figura 8 mostra o gráfico dos valores singulares do sistema em malha aberta, onde percebe-se a característica de uma função estritamente própria com freqüência de cruzamento de rad/s. 6
7 .8 λ,2 =.429±.3i.8 λ 6,7 =.9±.322i.6.6 abs(autovetor).4.2 abs(autovetor).4.2 u v w p q r phi theta u v w p q r phi theta (a) arfagem/ (b) deriva/ Figura 7. Magnitude dos autovetores associados a seus autovalores correspondentes λ valores singulares máximos valores singulares mínimos Valores singulares (db) Figura 8. Valores Singulares de G(s) em malha aberta. 4.2 Sistema Controlado A abordagem do projeto do controlador foi exposta na seção anterior. As quatro variáveis acopladas (φ, θ, ψ e ż) a serem controladas centralizadamente são avaliadas tanto no domínio da freqüência quanto no domínio do tempo. Com as funções de ponderação, descritas no anexo, foi atingido um gamma subótimo de., o que indica um grau de robustes adequado, considerando-se a complexidade do problema. A figura 9 mostra a sensibilidade S do sistema controlado. E2 para o e o não foi garantida. E2 para as velocidades de guinada e submersão foi garantida. A figura mostra a sensibilidade complementar do sistema T. Neste caso, E3 foi garantida para todos os sinais controlados. Também é importante observar que os sinais relativos às velocidades de guinada e submersão estão abaixo de db, ω, indicando a possível causa de porquê o sistema ser subatuado. A figura mostra a sensibilidade do controlador C do sistema controlado, o freqüência de cruzamento (Amplitude=dB) para os lemes é de 6, rad/s e 3, 98rad/s, respectivamente, o que garante E4. A resposta no domínio do tempo pode-ser avaliada utilizando o sinal degrau unitário. A figura 2 mostra esses resultados, observa-se que a estabilidade está bem garantida. De fato, no sistema sub-atuado o acoplamento de certas dinâmicas ainda está fortemente presente (/velocidade de guinada e /velocidade de submersão). Porém, esses acoplamentos adquirem pouca importância em veículos não tripulados, sempre que a estabilidade e o desempenho estejam garantidos. Estas respostas mostram que a especificação E é totalmente garantida, porém, o desempenho do sistema foi comprometido, portanto E não poderá ser garantido. 7
8 O controlador 2-GL é projetado com o objetivo de garantir a robustez do sistema tanto em estabilidade quanto em desempenho, através do préfiltro R e com as especificações dadas em E foram obtidas respostas mais rápidas e suaves em comparação com o controlador de um grau de liberdade. A figura 3 mostra o bom acompanhamento do sinal degrau, em todos os sinais controlados no sistema. Assim, o controlador 2-GL garante todas as especificações (E, E2, E3, E4 e E) do projeto do controlador para o sistema subatuado. A guiagem do VSA é muito boa e os resultados mostram bom acompanhamento dos sinais desejados. As figuras 4(a) e 4(b) mostram o acompanhamento de uma trajetória circular e o movimento dos lemes do VSA, respectivamente. As figuras 4(c) e 4(d) mostram o acompanhamento de uma trajetória zig-zag e o movimento dos lemes, respectivamente. Podem-se gerar inumeráveis resultados relativos ao acompanhamento de trajetórias, gerando-se até trajetórias espaciais como a figura (figura 4(f)), onde fica evidente o bom desempenho do controlador.. Conclusão Neste trabalho dois controladores centralizados foram projetados a partir do modelo do veículo submersível em 6-GL. Ambos foram projetados para controlar a dinâmica do sistema em seus seis graus de liberdade. O primeiro controlador (estrutura de -GL) mostrou ser muito conservador em relação ao segundo, com uma deficiência no tracking, mas em compensação é bem estável. O segundo Controlador garantiu, além da estabilidade, o bom desempenho do sistema. Conseqüentemente, a guiagem é feita a partir do segundo controlador (estrutura de 2-GL), as respostas indicam o bom acompanhamento de trajetórias. A estabilidade e desempenho robustos foram analisadas a partir dos gráficos de sensibilidade do sistema controlado, até que fôssem encontrados parâmetros que satisfizessem as especificações. Em seguida comprovou-se a resposta do sistema no domínio do tempo, os gráficos também avalizam a estabilidade e desempenho robustos. As dinâmicas de e guinada são fortemente acopladas, e ao não contar com atuadores independentes para esses movimentos o VSA é sub-atuado. O projeto do Controlador H demandou muito esforço na busca de parâmetros das funções de ponderação para um sistema sub-atuado e provavelmente é maior dificuldade a ser enfrentada por projetistas que utilizem esta técnica. 2 2 /WSφ /WSθ Sφ Sθ (a) (b) 3 /WS ψ /WSż 3 2 S ψ Sż (c) velocidade de guinada (d) velocidade de submersão Figura 9. Função de sensibilidade (S) e sua ponderação (/W s ) 8
9 /WTφ /WTθ Tφ Tθ (a) (b) /WT ψ /WTż T ψ Tż (c) velocidade de guinada (d) velocidade de submersão Figura. Função de sensibilidade (S) e sua ponderação (/W s ) 4 2 /WCδr Cδr /WCδs Cδs Freqüência, rad/s (a) leme vertical (b) leme horizontal Figura. Função de sensibilidade do controlador (C) e inversa da função de ponderação (/W C ) 9
10 . (a) (b). (c) (d) Figura 2. Resposta degrau unitária do modelo não linear controlado - Controlador -GL (a).2 (c).. 2 (b) 3 Figura 3. Resposta ao degrau, do modelo não linear controlado - Controlador 2-GL. (d)
11 4 trajetória desejada trajetória real leme vertical leme horizontal y (m) 2 2 Amplitude (em graus) x (m) (a) acompanhamento trajetória circular (b) movimento dos lemes 2 2 trajetória desejada trajetória real y (m) x (m) (c) acompanhamento trajetória zigzag Amplitude (em graus) leme vertical leme horizontal (d) movimento dos lemes 2 leme vertical leme horizontal Amplitude (em graus) (e) movimento do lemes (f) Posição do veículo Figura 4. Acompanhamento de trajetórias desejadas realizadas pelo veículo submersível autônomo
12 Referências CANHETTI, A. C. Modelo Livre de Submarinos. 47 p. Dissertação (Dissertação de Mestrado) Escola Politecnica/USP, São Paulo, 998. DONHA, D. C. Projeto de Sistemas de Controle Robustos Multivariáveis. São Paulo, Brasil: Poli-USP, 23. DONHA, D. C.; KATEBI, R. M. Automatic cost weigth selection in mixed sensitivity controller synthesis. In: CAMS 4. Proceedings of the IFAC Conference on Control Applications in Marine Systems. Ancona, Italy: Dipartimento di Ingegneria Informatica, e dell Automazione, Università Politecnica delle Marche, 24. p DONHA, D. C.; LUQUE, J. C. C. Six dof robust control. In: Proceedings of the International Control Conference. Glasgow, Scotland: University of Strathclyde, 26. FOSSEN, T. I. Guidance and Control of Ocean Vehicles. West Sussex PO9 UD, England: John Whiley & Sons, 994. HEALEY, A. J.; LIENARD, D. Multivariable sliding model control for unmanned underwater vehicles. IEEE journal of Oceanic Engineering, v. 8, n 3, p , 993. LOGAN, C. L. Robust controller design and evaluation for a small underwater vehicle. 36 p. Dissertação (Master s Thesis) Massachusetts Institute of Technology, Massachusetts Institute of Technology. Dept. of Electrical Engineering and Computer Science, 993. LUNDSTRöM, P.; SKOGESTAD, S.; DOYLE, J. Two-degree-of-freedom controller design for an ill-conditioned distillation process using µ-synthesis. Control, Communications and Signal Processing, 24. First International Symposium on, v. 7, n., p. 2 2, 999. MCEWEN, R. Modeling and Control of a Variable-Length AUV. Moss Landing, CA , 22. SILVESTRE, C.; PASCOAL, A. Depth control of the infante auv using. gain-scheduled reduced-order output feedback. In: CAMS. Proc. of 6th IFAC World Congress. Prague, Czech Republic, 2. SKOGESTAD, S.; POSTLETHWAITE, I. Multivariable Feedback Control. West Sussex PO9 UD, England: John Whiley & Sons, 996. SONG, F.; AN, E.; SMITH, S. M. Design robust nonlinear controllers for autonomous underwater vehicles with comparison of simulated and at-sea test data. Journal of Vibration and Control, v. 8(2), p , 22. SOUZA, E. C. Modelagem e Controle de Veículos Submarinos Não Tripulados. p. Dissertação (Dissertação de Mestrado) Escola Politecnica/USP, São Paulo, 23. TRIANTAFYLLOU, M. S.; HOVER, F. S. Maneuvering and Control of Marine Vehicles. Cambridge, Massachusetts, USA: The M.I.T. PRESS, 23. WHITCOMB, L. L. Underwater robotics: Out of the research. laboratory and into the field. International conference in Robotics and Automation, IEEE, Preprint of an invited paper to appear in the Special Session on Industrial Robotics, p. 6, 2. ZHOU, K.; DOYLE, J. C.; GLOVER, K. Robust and Optimal Control. [S.l.]: Prentice-Hall, Anexo A = 264 As matrizes do modelo linear usado na síntese do controlador foram as seguintes: 3.24e- 4.63e e e-24.e e 22.36e+.689e-.2998e e-23.96e e e 2.934e e-2.74e-2.487e e e e e+ 8.93e e e e-.379e e e e e e e-24.83e-2.364e e-.478e-.e+ 9.97e e-22.e+.4984e e-22 () 37 2
13 B = C = D = e-.494e e e e-2 37.e+.e+.4984e-22.e e e e-22.e+.27e-2 2.e+ 7 (6) 37 (7) [ ] S u = 8 /3 π /2 (9) 8 π S x = 8 π (2) 8 π 8 π 8 π S y = 8 π (2) π 8 As funções de ponderação usadas foram: W i = I 2 2 W d = I 4 4 W n = I 4 4 W model = I 4 4 (22) (8) W Sφ = s s s s s s W Sθ = s s s s s s W S ψ = s3 +.32s s s s 2 +.7s W Sż = s3 +.2s s + 7. s s s +.93 (23) W Tφ = s + W Tθ =.74.4s + W T ψ = s + W Tż = s + (24) s s W Cδr = e-8s e-3s s s W Cδs = e-8s e-3s (2) W Sφ W S = W Sθ W S ψ W Sż [ ] WCδr W C = W Cδs W T = W Tφ W Tθ W T ψ W Tż (26).76 s+.2.6 R = s s+.2 (28) s+. (27) 3
EXERCÍCIOS RESOLVIDOS
 ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
Controle Robusto H. 1. O problema de controle H. 2. Controle ótimo H por LMIs. 3. Patologia no controle H : altos ganhos. 3. Controle Misto H 2 /H
 Controle Robusto H 1. O problema de controle H 2. Controle ótimo H por LMIs 3. Patologia no controle H : altos ganhos 3. Controle Misto H 2 /H pag.1 Introdução ao Controle Robusto Aula 11 Controle H e
Controle Robusto H 1. O problema de controle H 2. Controle ótimo H por LMIs 3. Patologia no controle H : altos ganhos 3. Controle Misto H 2 /H pag.1 Introdução ao Controle Robusto Aula 11 Controle H e
Estabilidade no Domínio da Freqüência
 Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Engenharia de Controle
 Engenharia de Controle Prof. Fernando de Oliveira Souza Contato: Sala 2523 (BLOCO 1) e-mail: fosouza@cpdee.ufmg.br www.cpdee.ufmg.br/ fosouza Terças-feiras (20h55 às 22h35) e Sextas-feiras (19h00 às 20h40)
Engenharia de Controle Prof. Fernando de Oliveira Souza Contato: Sala 2523 (BLOCO 1) e-mail: fosouza@cpdee.ufmg.br www.cpdee.ufmg.br/ fosouza Terças-feiras (20h55 às 22h35) e Sextas-feiras (19h00 às 20h40)
11/07/2012. Professor Leonardo Gonsioroski FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA.
 FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
Modelagem no Domínio do Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO
 TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle
 Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle Espaço de Estados (CP1 www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 69 Roteiro 1 Modelo Não-Linear Modelo
Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle Espaço de Estados (CP1 www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 69 Roteiro 1 Modelo Não-Linear Modelo
SISTEMAS DE CONTROLE II
 SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
Utilização de um Veículo submersível em Tarefas de manutenção
 Utilização de um Veículo submersível em Tarefas de manutenção Prof. M. Sc. Juan C. C. Luque Departamento de Eletrotécnica, TECSUP, Arequipa-Perú Prof. Dr. Decio Crisol Donha Departamento de Engenharia
Utilização de um Veículo submersível em Tarefas de manutenção Prof. M. Sc. Juan C. C. Luque Departamento de Eletrotécnica, TECSUP, Arequipa-Perú Prof. Dr. Decio Crisol Donha Departamento de Engenharia
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções
 Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Controle II. Estudo e sintonia de controladores industriais
 Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Sistemas de Controle I (Servomecanismo) Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Sistemas de Controle I (Servomecanismo) Carlos Alexandre Mello 1 O que são sistemas de controle Um sistema de controle é um conjunto de componentes organizados de forma a conseguir a resposta desejada
Sistemas de Controle I (Servomecanismo) Carlos Alexandre Mello 1 O que são sistemas de controle Um sistema de controle é um conjunto de componentes organizados de forma a conseguir a resposta desejada
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos. Prof. Cassiano Rech cassiano@ieee.org
 Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Cálculo de volume de objetos utilizando câmeras RGB-D
 Cálculo de volume de objetos utilizando câmeras RGB-D Servílio Souza de ASSIS 1,3,4 ; Izadora Aparecida RAMOS 1,3,4 ; Bruno Alberto Soares OLIVEIRA 1,3 ; Marlon MARCON 2,3 1 Estudante de Engenharia de
Cálculo de volume de objetos utilizando câmeras RGB-D Servílio Souza de ASSIS 1,3,4 ; Izadora Aparecida RAMOS 1,3,4 ; Bruno Alberto Soares OLIVEIRA 1,3 ; Marlon MARCON 2,3 1 Estudante de Engenharia de
Introdução ao Projeto de Aeronaves. Aula 39 Relatório de Projeto Técnicas de Estruturação
 Introdução ao Projeto de Aeronaves Aula 39 Relatório de Projeto Técnicas de Estruturação Tópicos Abordados Relatório de Projeto. Técnicas de Estruturação para uma boa Avaliação. Elaboração do Relatório
Introdução ao Projeto de Aeronaves Aula 39 Relatório de Projeto Técnicas de Estruturação Tópicos Abordados Relatório de Projeto. Técnicas de Estruturação para uma boa Avaliação. Elaboração do Relatório
MICROMASTER MM4. Usando o Controle de Malha Fechada (PID) Edição 08.2002. IND 1 Drives technology Suporte Técnico Drives Hotline
 s MICROMASTER MM4 Usando o Controle de Malha Fechada (PID) Edição 08.2002 IND 1 Drives technology Suporte Técnico Drives Hotline USANDO O CONTROLE DE MALHA FECHADA NO MM4 O que é controle de malha fechada
s MICROMASTER MM4 Usando o Controle de Malha Fechada (PID) Edição 08.2002 IND 1 Drives technology Suporte Técnico Drives Hotline USANDO O CONTROLE DE MALHA FECHADA NO MM4 O que é controle de malha fechada
CAPÍTULO 1 INTRODUÇÃO, OBJETIVOS, JUSTIFICATIVAS E ORGANIZAÇÃO DO TRABALHO
 CAPÍTULO 1 INTRODUÇÃO, OBJETIVOS, JUSTIFICATIVAS E ORGANIZAÇÃO DO TRABALHO 1.1 - INTRODUÇÃO Com o aumento da demanda de serviços de tecnologia e também buscando atender às necessidades atuais do progresso
CAPÍTULO 1 INTRODUÇÃO, OBJETIVOS, JUSTIFICATIVAS E ORGANIZAÇÃO DO TRABALHO 1.1 - INTRODUÇÃO Com o aumento da demanda de serviços de tecnologia e também buscando atender às necessidades atuais do progresso
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:
![O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:](/thumbs/27/10931177.jpg) 4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
Ajuste dos Parâmetros de um Controlador PI em uma Coluna de Destilação Binária
 Ajuste dos Parâmetros de um Controlador PI em uma Coluna de Destilação Binária Marina Roberto Martins 1*, Fernando Palú 1 (1) Universidade Estadual do Oeste do Paraná, Curso de Engenharia Química. e-mail:
Ajuste dos Parâmetros de um Controlador PI em uma Coluna de Destilação Binária Marina Roberto Martins 1*, Fernando Palú 1 (1) Universidade Estadual do Oeste do Paraná, Curso de Engenharia Química. e-mail:
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação
 Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
Curso Automação Industrial Aula 2 Estrutura e características Gerais dos Robôs. Prof. Giuliano Gozzi Disciplina: CNC - Robótica
 Curso Automação Industrial Aula 2 Estrutura e características Gerais dos Robôs Prof. Giuliano Gozzi Disciplina: CNC - Robótica Cronograma Introdução a Robótica Estrutura e Características Gerais dos Robôs
Curso Automação Industrial Aula 2 Estrutura e características Gerais dos Robôs Prof. Giuliano Gozzi Disciplina: CNC - Robótica Cronograma Introdução a Robótica Estrutura e Características Gerais dos Robôs
TTT-PLOT E TESTE DE HIPÓTESES BOOTSTRAP PARA O MODELO BI-WEIBULL. Cleber Giugioli Carrasco 1 ; Francisco Louzada-Neto 2 RESUMO
 TTT-PLOT E TESTE DE HIPÓTESES BOOTSTRAP PARA O MODELO BI-WEIBULL Cleber Giugioli Carrasco ; Francisco Louzada-Neto Curso de Matemática, Unidade Universitária de Ciências Exatas e Tecnológicas, UEG. Departamento
TTT-PLOT E TESTE DE HIPÓTESES BOOTSTRAP PARA O MODELO BI-WEIBULL Cleber Giugioli Carrasco ; Francisco Louzada-Neto Curso de Matemática, Unidade Universitária de Ciências Exatas e Tecnológicas, UEG. Departamento
IW10. Rev.: 02. Especificações Técnicas
 IW10 Rev.: 02 Especificações Técnicas Sumário 1. INTRODUÇÃO... 1 2. COMPOSIÇÃO DO IW10... 2 2.1 Placa Principal... 2 2.2 Módulos de Sensores... 5 3. APLICAÇÕES... 6 3.1 Monitoramento Local... 7 3.2 Monitoramento
IW10 Rev.: 02 Especificações Técnicas Sumário 1. INTRODUÇÃO... 1 2. COMPOSIÇÃO DO IW10... 2 2.1 Placa Principal... 2 2.2 Módulos de Sensores... 5 3. APLICAÇÕES... 6 3.1 Monitoramento Local... 7 3.2 Monitoramento
Controle de Veículos Aéreos
 12, 13 e 14/11/2014, Parnaíba-PI Controle de Veículos Aéreos Prof. Dr. Mário Sarcinelli Filho Universidade Federal do Espírito Santo UFES Bolsista de Produtividade em Pesquisa PQ-2 do CNPq Orientador de
12, 13 e 14/11/2014, Parnaíba-PI Controle de Veículos Aéreos Prof. Dr. Mário Sarcinelli Filho Universidade Federal do Espírito Santo UFES Bolsista de Produtividade em Pesquisa PQ-2 do CNPq Orientador de
Redes de Computadores sem Fio
 Redes de Computadores sem Fio Prof. Marcelo Gonçalves Rubinstein Programa de Pós-Graduação em Engenharia Eletrônica Faculdade de Engenharia Universidade do Estado do Rio de Janeiro Programa Introdução
Redes de Computadores sem Fio Prof. Marcelo Gonçalves Rubinstein Programa de Pós-Graduação em Engenharia Eletrônica Faculdade de Engenharia Universidade do Estado do Rio de Janeiro Programa Introdução
ROBUST, FRAGILE OR OPTIMAL? REVISITADO: UMA CONDIÇÃO NECESSÁRIA E SUFICIENTE PARA A FRAGILIDADE DE CONTROLADORES. Marcos V. Moreira, João C.
 ROBUST, FRAGILE OR OPTIMAL? REVISITADO: UMA CONDIÇÃO NECESSÁRIA E SUFICIENTE PARA A FRAGILIDADE DE CONTROLADORES Marcos V. Moreira, João C. Basilio, Universidade Federal do Rio de Janeiro COPPE - Programa
ROBUST, FRAGILE OR OPTIMAL? REVISITADO: UMA CONDIÇÃO NECESSÁRIA E SUFICIENTE PARA A FRAGILIDADE DE CONTROLADORES Marcos V. Moreira, João C. Basilio, Universidade Federal do Rio de Janeiro COPPE - Programa
Mecânica: processos industriais: usinagem, laminação, fundição, solda, prensagem, vapor, gás. Automóveis, suspensão, motor, câmbio.
 1 Disciplina de Sistemas de Controle Prof. Luciano Menegaldo e-mail: lmeneg@ime.eb.br home-page: http://lmeneg-aulas.tripod.com Aula 1 Introdução 1. Idéias gerais e exemplos de sistemas de controle - Assunto
1 Disciplina de Sistemas de Controle Prof. Luciano Menegaldo e-mail: lmeneg@ime.eb.br home-page: http://lmeneg-aulas.tripod.com Aula 1 Introdução 1. Idéias gerais e exemplos de sistemas de controle - Assunto
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Desempenho de Sistemas de Controle Realimentados
 Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
6 Conclusões e Trabalhos futuros 6.1. Conclusões
 6 Conclusões e Trabalhos futuros 6.1. Conclusões Neste trabalho estudou-se o comportamento do sistema que foi denominado pendulo planar com a adição de uma roda de reação na haste do pendulo composta de
6 Conclusões e Trabalhos futuros 6.1. Conclusões Neste trabalho estudou-se o comportamento do sistema que foi denominado pendulo planar com a adição de uma roda de reação na haste do pendulo composta de
CONTROLE ATIVO DE VIBRAÇÃO EM SUSPENSÃO DE BARRAS PARA PULVERIZADORES AGRÍCOLAS TRACIONADOS
 CONTROLE ATIVO DE VIBRAÇÃO EM SUSPENSÃO DE BARRAS PARA PULVERIZADORES... 1 CONTROLE ATIVO DE VIBRAÇÃO EM SUSPENSÃO DE BARRAS PARA PULVERIZADORES AGRÍCOLAS TRACIONADOS Cristiano Okada Pontelli Máquinas
CONTROLE ATIVO DE VIBRAÇÃO EM SUSPENSÃO DE BARRAS PARA PULVERIZADORES... 1 CONTROLE ATIVO DE VIBRAÇÃO EM SUSPENSÃO DE BARRAS PARA PULVERIZADORES AGRÍCOLAS TRACIONADOS Cristiano Okada Pontelli Máquinas
Movimento Retilíneo Uniforme (MRU) Equação Horária do MRU
 Movimento Retilíneo Uniforme (MRU) velocímetro do automóvel da figura abaixo marca sempre a mesma velocidade. Quando um móvel possui sempre a mesma velocidade e se movimenta sobre uma reta dizemos que
Movimento Retilíneo Uniforme (MRU) velocímetro do automóvel da figura abaixo marca sempre a mesma velocidade. Quando um móvel possui sempre a mesma velocidade e se movimenta sobre uma reta dizemos que
Introdução teórica aula 6: Capacitores
 Introdução teórica aula 6: Capacitores Capacitores O capacitor é um elemento capaz de armazenar energia. É formado por um par de superfícies condutoras separadas por um material dielétrico ou vazio. A
Introdução teórica aula 6: Capacitores Capacitores O capacitor é um elemento capaz de armazenar energia. É formado por um par de superfícies condutoras separadas por um material dielétrico ou vazio. A
SISTEMA DE APONTAMENTO
 Introdução SISTEMA DE APONTAMENTO Alunos: Lucas Castro Faria Carolina do Amaral Galhardo Orientador: Hans Ingo Weber Foi feito um estudo para aquisição de dados através da placa NI USB-6229, usando o programa
Introdução SISTEMA DE APONTAMENTO Alunos: Lucas Castro Faria Carolina do Amaral Galhardo Orientador: Hans Ingo Weber Foi feito um estudo para aquisição de dados através da placa NI USB-6229, usando o programa
1 Descrição do Trabalho
 Departamento de Informática - UFES 1 o Trabalho Computacional de Algoritmos Numéricos - 13/2 Métodos de Runge-Kutta e Diferenças Finitas Prof. Andréa Maria Pedrosa Valli Data de entrega: Dia 23 de janeiro
Departamento de Informática - UFES 1 o Trabalho Computacional de Algoritmos Numéricos - 13/2 Métodos de Runge-Kutta e Diferenças Finitas Prof. Andréa Maria Pedrosa Valli Data de entrega: Dia 23 de janeiro
Funções de Posicionamento para Controle de Eixos
 Funções de Posicionamento para Controle de Eixos Resumo Atualmente muitos Controladores Programáveis (CPs) classificados como de pequeno porte possuem, integrados em um único invólucro, uma densidade significativa
Funções de Posicionamento para Controle de Eixos Resumo Atualmente muitos Controladores Programáveis (CPs) classificados como de pequeno porte possuem, integrados em um único invólucro, uma densidade significativa
MODIFICAÇÃO DO TESTE DE NORMALIDADE DE SHAPIRO-WILK MULTIVARIADO DO SOFTWARE ESTATÍSTICO R
 MODIFICAÇÃO DO TESTE DE NORMALIDADE DE SHAPIRO-WILK MULTIVARIADO DO SOFTWARE ESTATÍSTICO R Roberta Bessa Veloso 1, Daniel Furtado Ferreira 2, Eric Batista Ferreira 3 INTRODUÇÃO A inferência estatística
MODIFICAÇÃO DO TESTE DE NORMALIDADE DE SHAPIRO-WILK MULTIVARIADO DO SOFTWARE ESTATÍSTICO R Roberta Bessa Veloso 1, Daniel Furtado Ferreira 2, Eric Batista Ferreira 3 INTRODUÇÃO A inferência estatística
Me todos de Ajuste de Controladores
 Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Introdução e Motivação
 Introdução e Motivação 1 Análise de sistemas enfoque: sistemas dinâmicos; escopo: sistemas lineares; objetivo: representar, por meio de modelos matemáticos, fenômenos observados e sistemas de interesse;
Introdução e Motivação 1 Análise de sistemas enfoque: sistemas dinâmicos; escopo: sistemas lineares; objetivo: representar, por meio de modelos matemáticos, fenômenos observados e sistemas de interesse;
Universidade Federal de Pernambuco
 Universidade Federal de Pernambuco Graduação em Engenharia da Computação Centro de Informática 2D Feature Distance Estimation for Indoor Environments using 2D laser range data Proposta de Trabalho de Graduação
Universidade Federal de Pernambuco Graduação em Engenharia da Computação Centro de Informática 2D Feature Distance Estimation for Indoor Environments using 2D laser range data Proposta de Trabalho de Graduação
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial. Transformada de Laplace
 Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
SISTEMAS COM AMORTECIMENTO NÃO-PROPORCIONAL NO DOMÍNIO DA FREQÜÊNCIA
 SISTEMAS COM AMORTECIMENTO NÃO-PROPORCIONAL NO DOMÍNIO DA FREQÜÊNCIA Zacarias Martin Chamberlain Pravia Professor - Faculdade de Engenharia e Arquitetura - Universidade de Passo Fundo/UFP zacarias@upf.br
SISTEMAS COM AMORTECIMENTO NÃO-PROPORCIONAL NO DOMÍNIO DA FREQÜÊNCIA Zacarias Martin Chamberlain Pravia Professor - Faculdade de Engenharia e Arquitetura - Universidade de Passo Fundo/UFP zacarias@upf.br
TriNMPC. Controlador Preditivo Multivariável Linear e Não-linear BENEFÍCIOS: APLICAÇÕES: CARACTERÍSTICAS:
 TriNMPC Controlador Preditivo Multivariável Linear e Não-linear O software TriNMPC é um controlador preditivo multivariável que pode ser tanto linear como nãolinear, sendo extremamente versátil e de fácil
TriNMPC Controlador Preditivo Multivariável Linear e Não-linear O software TriNMPC é um controlador preditivo multivariável que pode ser tanto linear como nãolinear, sendo extremamente versátil e de fácil
RELATÓRIO FINAL: PROJETO DESAFIO CONTROLE DE POSIÇÃO DE UMA VÁLVULA
 RELATÓRIO FINAL: PROJETO DESAFIO CONTROLE DE POSIÇÃO DE UMA VÁLVULA Laboratório de Controle e Automação 1 ( LECI 1 ) Professor: Reinaldo Martinez Palhares Integrantes: Henrique Goseling Araújo, Hugo Montalvão
RELATÓRIO FINAL: PROJETO DESAFIO CONTROLE DE POSIÇÃO DE UMA VÁLVULA Laboratório de Controle e Automação 1 ( LECI 1 ) Professor: Reinaldo Martinez Palhares Integrantes: Henrique Goseling Araújo, Hugo Montalvão
ESTUDO DE CASO: LeCS: Ensino a Distância
 ESTUDO DE CASO: LeCS: Ensino a Distância HERMOSILLA, Lígia Docente da Faculdade de Ciências Jurídicas e Gerenciais de Garça FAEG - Labienópolis - CEP 17400-000 Garça (SP) Brasil Telefone (14) 3407-8000
ESTUDO DE CASO: LeCS: Ensino a Distância HERMOSILLA, Lígia Docente da Faculdade de Ciências Jurídicas e Gerenciais de Garça FAEG - Labienópolis - CEP 17400-000 Garça (SP) Brasil Telefone (14) 3407-8000
Controle de Processos: Introdução
 Controle de Processos: Introdução Prof. Eduardo Stockler Tognetti & David Fiorillo Laboratório de Automação e Robótica (LARA) Dept. Engenharia Elétrica - UnB Conteúdo 1. Panorama da engenharia de controle
Controle de Processos: Introdução Prof. Eduardo Stockler Tognetti & David Fiorillo Laboratório de Automação e Robótica (LARA) Dept. Engenharia Elétrica - UnB Conteúdo 1. Panorama da engenharia de controle
Arquiteturas RISC. (Reduced Instructions Set Computers)
 Arquiteturas RISC (Reduced Instructions Set Computers) 1 INOVAÇÕES DESDE O SURGIMENTO DO COMPU- TADOR DE PROGRAMA ARMAZENADO (1950)! O conceito de família: desacoplamento da arquitetura de uma máquina
Arquiteturas RISC (Reduced Instructions Set Computers) 1 INOVAÇÕES DESDE O SURGIMENTO DO COMPU- TADOR DE PROGRAMA ARMAZENADO (1950)! O conceito de família: desacoplamento da arquitetura de uma máquina
Sistema de excitação
 Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
MEDIDAS MAGNÉTICAS DE PINTURAS EM CERÂMICA E PINTURAS RUPESTRES
 MEDIDAS MAGNÉTICAS DE PINTURAS EM CERÂMICA E PINTURAS RUPESTRES Aluno: Fernando Cardoso Emiliano Ribeiro Orientador: Paulo Costa Ribeiro Introdução Realizamos no campo de medidas magnéticas de vasos e
MEDIDAS MAGNÉTICAS DE PINTURAS EM CERÂMICA E PINTURAS RUPESTRES Aluno: Fernando Cardoso Emiliano Ribeiro Orientador: Paulo Costa Ribeiro Introdução Realizamos no campo de medidas magnéticas de vasos e
DESENVOLVIMENTO DE PROGRAMA MULTIMIDIA PARA O ENSINO DEDINÂMICA DE MÚLTIPLOS CORPOS
 DESENVOLVIMENTO DE PROGRAMA MULTIMIDIA PARA O ENSINO DEDINÂMICA DE MÚLTIPLOS CORPOS Ilmar Ferreira Santos Rodrigo Fernandes de Carvalho UNICAMP - Faculdade de Engenharia Mecânica Departamento de Projeto
DESENVOLVIMENTO DE PROGRAMA MULTIMIDIA PARA O ENSINO DEDINÂMICA DE MÚLTIPLOS CORPOS Ilmar Ferreira Santos Rodrigo Fernandes de Carvalho UNICAMP - Faculdade de Engenharia Mecânica Departamento de Projeto
computador-cálculo numérico perfeita. As fases na resolução de um problema real podem, de modo geral, ser colocadas na seguinte ordem:
 1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
PLANTA DIDÁTICA COMANDADA VIA SUPERVISÓRIO
 PLANTA DIDÁTICA COMANDADA VIA SUPERVISÓRIO Aline Lima Silva¹; Danilo Menezes de Abreu²; Jailson da silva Machado³; Alexandre Teles 4 (orientador) ¹Faculdade de Engenharia de Resende. Resende - RJ alinel-silva@hotmail.com
PLANTA DIDÁTICA COMANDADA VIA SUPERVISÓRIO Aline Lima Silva¹; Danilo Menezes de Abreu²; Jailson da silva Machado³; Alexandre Teles 4 (orientador) ¹Faculdade de Engenharia de Resende. Resende - RJ alinel-silva@hotmail.com
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Não Linear Aula 25: Programação Não-Linear - Funções de Uma única variável Mínimo; Mínimo Global; Mínimo Local; Optimização Irrestrita; Condições Óptimas; Método da Bissecção; Método de Newton.
1 Programação Não Linear Aula 25: Programação Não-Linear - Funções de Uma única variável Mínimo; Mínimo Global; Mínimo Local; Optimização Irrestrita; Condições Óptimas; Método da Bissecção; Método de Newton.
Controlador DMC-Dynamic Matrix Control
 Capítulo 7 Controlador DMC-Dynamic Matrix Control 7.1 Introdução Em 1979, Cluter e Ramaker apresentaram um algoritmo preditivo,o controlador DMC, como uma metodologia capaz de manipular restrições operacionais
Capítulo 7 Controlador DMC-Dynamic Matrix Control 7.1 Introdução Em 1979, Cluter e Ramaker apresentaram um algoritmo preditivo,o controlador DMC, como uma metodologia capaz de manipular restrições operacionais
PESQUISA OPERACIONAL: UMA ABORDAGEM À PROGRAMAÇÃO LINEAR. Rodolfo Cavalcante Pinheiro 1,3 Cleber Giugioli Carrasco 2,3 *
 PESQUISA OPERACIONAL: UMA ABORDAGEM À PROGRAMAÇÃO LINEAR 1 Graduando Rodolfo Cavalcante Pinheiro 1,3 Cleber Giugioli Carrasco 2,3 * 2 Pesquisador - Orientador 3 Curso de Matemática, Unidade Universitária
PESQUISA OPERACIONAL: UMA ABORDAGEM À PROGRAMAÇÃO LINEAR 1 Graduando Rodolfo Cavalcante Pinheiro 1,3 Cleber Giugioli Carrasco 2,3 * 2 Pesquisador - Orientador 3 Curso de Matemática, Unidade Universitária
Correlação Canônica. Outubro / 1998. Versão preliminar. Fabio Vessoni. fabio@mv2.com.br (011) 30642254. MV2 Sistemas de Informação
 Correlação Canônica Outubro / 998 Versão preliminar Fabio Vessoni fabio@mv.com.br (0) 306454 MV Sistemas de Informação Introdução Existem várias formas de analisar dois conjuntos de dados. Um dos modelos
Correlação Canônica Outubro / 998 Versão preliminar Fabio Vessoni fabio@mv.com.br (0) 306454 MV Sistemas de Informação Introdução Existem várias formas de analisar dois conjuntos de dados. Um dos modelos
Francisca Raquel de Vasconcelos Silveira Gustavo Augusto Lima de Campos Mariela Inés Cortés
 Francisca Raquel de Vasconcelos Silveira Gustavo Augusto Lima de Campos Mariela Inés Cortés Introdução Trabalhos Relacionados Abordagem Proposta Considerações Finais Conclusão Trabalhos Futuros 2 Agentes
Francisca Raquel de Vasconcelos Silveira Gustavo Augusto Lima de Campos Mariela Inés Cortés Introdução Trabalhos Relacionados Abordagem Proposta Considerações Finais Conclusão Trabalhos Futuros 2 Agentes
1 Propagação de Onda Livre ao Longo de um Guia de Ondas Estreito.
 1 I-projeto do campus Programa Sobre Mecânica dos Fluidos Módulos Sobre Ondas em Fluidos T. R. Akylas & C. C. Mei CAPÍTULO SEIS ONDAS DISPERSIVAS FORÇADAS AO LONGO DE UM CANAL ESTREITO As ondas de gravidade
1 I-projeto do campus Programa Sobre Mecânica dos Fluidos Módulos Sobre Ondas em Fluidos T. R. Akylas & C. C. Mei CAPÍTULO SEIS ONDAS DISPERSIVAS FORÇADAS AO LONGO DE UM CANAL ESTREITO As ondas de gravidade
Processos em Engenharia: Modelagem Matemática de Sistemas Fluídicos
 Processos em Engenharia: Modelagem Matemática de Sistemas Fluídicos Prof. Daniel Coutinho coutinho@das.ufsc.br Departamento de Automação e Sistemas DAS Universidade Federal de Santa Catarina UFSC DAS 5101
Processos em Engenharia: Modelagem Matemática de Sistemas Fluídicos Prof. Daniel Coutinho coutinho@das.ufsc.br Departamento de Automação e Sistemas DAS Universidade Federal de Santa Catarina UFSC DAS 5101
Universidade Federal de Ouro Preto Escola de Minas DECIV. Gestão de Obras em Construção Civil. Aula 3 PLANEJAMENTO DE OBRAS
 Universidade Federal de Ouro Preto Escola de Minas DECIV CIV 43 Aula 3 PLANEJAMENTO DE OBRAS SISTEMA DE PLANEJAMENTO DE OBRAS DEFINIÇÃO DE PLANEJAMENTO a palavra: Visão a sentença: Planejamento é uma ferramenta
Universidade Federal de Ouro Preto Escola de Minas DECIV CIV 43 Aula 3 PLANEJAMENTO DE OBRAS SISTEMA DE PLANEJAMENTO DE OBRAS DEFINIÇÃO DE PLANEJAMENTO a palavra: Visão a sentença: Planejamento é uma ferramenta
Ensaio de Emissão Acústica Aplicado em Cilindros sem Costura para Armazenamento de Gases
 Ensaio de Emissão Acústica Aplicado em Cilindros sem Costura para Armazenamento de Gases Pedro Feres Filho São Paulo, Brasil e-mail: pedro@pasa.com.br 1- Resumo Este trabalho teve como objetivo apresentar
Ensaio de Emissão Acústica Aplicado em Cilindros sem Costura para Armazenamento de Gases Pedro Feres Filho São Paulo, Brasil e-mail: pedro@pasa.com.br 1- Resumo Este trabalho teve como objetivo apresentar
6. Geometria, Primitivas e Transformações 3D
 6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO. Professor Leonardo Gonsioroski
 ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
EDUCAÇÃO A DISTÂNCIA: UMA FORMA DE INCLUSÃO DO DEFICIENTE VISUAL À EDUCAÇÃO SUPERIOR
 EDUCAÇÃO A DISTÂNCIA: UMA FORMA DE INCLUSÃO DO DEFICIENTE VISUAL À EDUCAÇÃO SUPERIOR José Oscar Fontanini de Carvalho Pontifícia Universidade Católica de Campinas - PUC-Campinas (oscar@ii.puc-campinas.br)
EDUCAÇÃO A DISTÂNCIA: UMA FORMA DE INCLUSÃO DO DEFICIENTE VISUAL À EDUCAÇÃO SUPERIOR José Oscar Fontanini de Carvalho Pontifícia Universidade Católica de Campinas - PUC-Campinas (oscar@ii.puc-campinas.br)
Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia
 Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia Oscilações 1. Movimento Oscilatório. Cinemática do Movimento Harmônico Simples (MHS) 3. MHS e Movimento
Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia Oscilações 1. Movimento Oscilatório. Cinemática do Movimento Harmônico Simples (MHS) 3. MHS e Movimento
Técnicas para Programação Inteira e Aplicações em Problemas de Roteamento de Veículos 14
 1 Introdução O termo "roteamento de veículos" está relacionado a um grande conjunto de problemas de fundamental importância para a área de logística de transportes, em especial no que diz respeito ao uso
1 Introdução O termo "roteamento de veículos" está relacionado a um grande conjunto de problemas de fundamental importância para a área de logística de transportes, em especial no que diz respeito ao uso
FAPERJ & PIUES/PUC-Rio FÍSICA E MATEMÁTICA DO ENSINO MÉDIO APLICADAS A SISTEMAS DE ENGENHARIA
 FAPERJ & PIUES/PUC-Rio FÍSICA E MATEMÁTICA DO ENSINO MÉDIO APLICADAS A SISTEMAS DE ENGENHARIA 1) INTRODUÇÃO Rio de Janeiro, 05 de Maio de 2015. A equipe desenvolvedora deste projeto conta com: - Prof.
FAPERJ & PIUES/PUC-Rio FÍSICA E MATEMÁTICA DO ENSINO MÉDIO APLICADAS A SISTEMAS DE ENGENHARIA 1) INTRODUÇÃO Rio de Janeiro, 05 de Maio de 2015. A equipe desenvolvedora deste projeto conta com: - Prof.
Aula 2. Carlos Amaral Fonte: Cristiano Quevedo Andrea
 Aula 2 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Agosto de 2011. Resumo Terminologias 1
Aula 2 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Agosto de 2011. Resumo Terminologias 1
CENTRO UNIVERSITÁRIO ESTÁCIO RADIAL DE SÃO PAULO SÍNTESE DO PROJETO PEDAGÓGICO DE CURSO 1
 SÍNTESE DO PROJETO PEDAGÓGICO DE CURSO 1 CURSO: ANÁLISE E DESENVOLVIMENTO DE SISTEMAS MISSÃO DO CURSO A concepção do curso de Análise e Desenvolvimento de Sistemas está alinhada a essas novas demandas
SÍNTESE DO PROJETO PEDAGÓGICO DE CURSO 1 CURSO: ANÁLISE E DESENVOLVIMENTO DE SISTEMAS MISSÃO DO CURSO A concepção do curso de Análise e Desenvolvimento de Sistemas está alinhada a essas novas demandas
Emails: jean@dee.feis.unesp.br, andrelexandre@bol.com.br, jpaulo@dee.feis.unesp.br, lizetega@mat.feis.unesp.br, giapolinario@yahoo.com.
 18 a 21 de setembro de 211 CONTROLE EXPERIMENTAL DO PÊNDULO INVERTIDO CONSIDERANDO ATRASO COMPUTACIONAL Jean M. S. Ribeiro, André Luiz A. de Paula, José Paulo F. Garcia, Lizete Maria C. F. Garcia, Gisele
18 a 21 de setembro de 211 CONTROLE EXPERIMENTAL DO PÊNDULO INVERTIDO CONSIDERANDO ATRASO COMPUTACIONAL Jean M. S. Ribeiro, André Luiz A. de Paula, José Paulo F. Garcia, Lizete Maria C. F. Garcia, Gisele
Controle de Múltiplos Pivôs Centrais com um único Conjunto Motor-Bomba
 Controle de Múltiplos Pivôs Centrais com um único Conjunto Motor-Bomba Thiago de Lima MUNIZ, Bernardo Pinheiro de ALVARENGA, José Wilson de Lima NERYS, Antônio Marcos de Melo MEDEIROS Escola de Engenharia
Controle de Múltiplos Pivôs Centrais com um único Conjunto Motor-Bomba Thiago de Lima MUNIZ, Bernardo Pinheiro de ALVARENGA, José Wilson de Lima NERYS, Antônio Marcos de Melo MEDEIROS Escola de Engenharia
Conforme explicado em 2.4.3, o sinal de voz x(n) às vezes é alterado com a adição de ruído r(n), resultando num sinal corrompido y(n).
 4 Wavelet Denoising O capítulo 3 abordou a questão do ruído durante a extração dos atributos as técnicas do SSCH e do PNCC, por exemplo, extraem com mais robustez a informação da voz a partir de um sinal
4 Wavelet Denoising O capítulo 3 abordou a questão do ruído durante a extração dos atributos as técnicas do SSCH e do PNCC, por exemplo, extraem com mais robustez a informação da voz a partir de um sinal
INTRODUÇÃO. Tradução: fora da terra. Mais empregado como a área da plataforma continental até uma lâmina d água de 2000 metros, no caso do Brasil.
 INTRODUÇÃO 1. OFF-SHORE Tradução: fora da terra. Mais empregado como a área da plataforma continental até uma lâmina d água de 2000 metros, no caso do Brasil. 2. O MEIO AMBIENTE Vento Age nas partes expostas
INTRODUÇÃO 1. OFF-SHORE Tradução: fora da terra. Mais empregado como a área da plataforma continental até uma lâmina d água de 2000 metros, no caso do Brasil. 2. O MEIO AMBIENTE Vento Age nas partes expostas
Instituto de Computação, Universidade Federal do Amazonas (UFAM) Manaus-AM, Brasil
 Elicitação de Requisitos a partir de Modelos de Processos de Negócio e Modelos Organizacionais: Uma pesquisa para definição de técnicas baseadas em heurísticas Marcos A. B. de Oliveira 1, Sérgio R. C.
Elicitação de Requisitos a partir de Modelos de Processos de Negócio e Modelos Organizacionais: Uma pesquisa para definição de técnicas baseadas em heurísticas Marcos A. B. de Oliveira 1, Sérgio R. C.
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
5 Transformadas de Laplace
 5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
AULA #12. Estabilidade de Sistemas de Controle por
 AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
Desenvolvendo uma Arquitetura de Componentes Orientada a Serviço SCA
 Desenvolvendo uma Arquitetura de Componentes Orientada a Serviço SCA RESUMO Ricardo Della Libera Marzochi A introdução ao Service Component Architecture (SCA) diz respeito ao estudo dos principais fundamentos
Desenvolvendo uma Arquitetura de Componentes Orientada a Serviço SCA RESUMO Ricardo Della Libera Marzochi A introdução ao Service Component Architecture (SCA) diz respeito ao estudo dos principais fundamentos
aplicada a problemas de poluição do ar
 Biomatemática 17 (2007), 21 34 ISSN 1679-365X Uma Publicação do Grupo de Biomatemática IMECC UNICAMP Programação matemática fuzzy aplicada a problemas de poluição do ar Luiza A. Pinto Cantão 1, Depto.
Biomatemática 17 (2007), 21 34 ISSN 1679-365X Uma Publicação do Grupo de Biomatemática IMECC UNICAMP Programação matemática fuzzy aplicada a problemas de poluição do ar Luiza A. Pinto Cantão 1, Depto.
DESENVOLVIMENTO DE UMA PLATAFORMA PARA SIMULAÇÃO DE SATÉLITES. Angelo dos Santos Lunardi 1 ; Rodrigo Alvite Romano 2.
 DESENVOLVIMENTO DE UMA PLATAFORMA PARA SIMULAÇÃO DE SATÉLITES Angelo dos Santos Lunardi 1 ; Rodrigo Alvite Romano 2. 1 Aluno de Iniciação Científica da Escola de Engenharia Mauá (EEM/CEUN-IMT); 2 Professor
DESENVOLVIMENTO DE UMA PLATAFORMA PARA SIMULAÇÃO DE SATÉLITES Angelo dos Santos Lunardi 1 ; Rodrigo Alvite Romano 2. 1 Aluno de Iniciação Científica da Escola de Engenharia Mauá (EEM/CEUN-IMT); 2 Professor
MIEC MESTRADO INTEGRADO EM ENGENHARIA CIVIL 2014/2015 PROPOSTA DE TEMAS PARA DISSERTAÇÃO RAMO DE ESPECIALIZAÇÃO/ ÁREA CIENTÍFICA: ESTRUTURAS
 1 EST1 AVALIAÇÃO DA CAPACIDADE DE DEFORMAÇÃO DE ELEMENTOS TUBULARES EM AÇO José Miguel Castro CO Um dos passos essenciais no processo de avaliação da segurança sísmica de estruturas consiste na comparação
1 EST1 AVALIAÇÃO DA CAPACIDADE DE DEFORMAÇÃO DE ELEMENTOS TUBULARES EM AÇO José Miguel Castro CO Um dos passos essenciais no processo de avaliação da segurança sísmica de estruturas consiste na comparação
Medição tridimensional
 A U A UL LA Medição tridimensional Um problema O controle de qualidade dimensional é tão antigo quanto a própria indústria, mas somente nas últimas décadas vem ocupando a importante posição que lhe cabe.
A U A UL LA Medição tridimensional Um problema O controle de qualidade dimensional é tão antigo quanto a própria indústria, mas somente nas últimas décadas vem ocupando a importante posição que lhe cabe.
TRABALHOS TÉCNICOS Coordenação de Documentação e Informação INOVAÇÃO E GERENCIAMENTO DE PROCESSOS: UMA ANÁLISE BASEADA NA GESTÃO DO CONHECIMENTO
 TRABALHOS TÉCNICOS Coordenação de Documentação e Informação INOVAÇÃO E GERENCIAMENTO DE PROCESSOS: UMA ANÁLISE BASEADA NA GESTÃO DO CONHECIMENTO INTRODUÇÃO Os processos empresariais são fluxos de valor
TRABALHOS TÉCNICOS Coordenação de Documentação e Informação INOVAÇÃO E GERENCIAMENTO DE PROCESSOS: UMA ANÁLISE BASEADA NA GESTÃO DO CONHECIMENTO INTRODUÇÃO Os processos empresariais são fluxos de valor
Gerenciamento de Riscos do Projeto Eventos Adversos
 Gerenciamento de Riscos do Projeto Eventos Adversos 11. Gerenciamento de riscos do projeto PMBOK 2000 PMBOK 2004 11.1 Planejamento de gerenciamento de riscos 11.1 Planejamento de gerenciamento de riscos
Gerenciamento de Riscos do Projeto Eventos Adversos 11. Gerenciamento de riscos do projeto PMBOK 2000 PMBOK 2004 11.1 Planejamento de gerenciamento de riscos 11.1 Planejamento de gerenciamento de riscos
Processos industriais INSTRUMENTAÇÃO E CONTROLE. Pirâmide da automação 29/1/2012. Controle automático de processo
 Processos industriais INSTRUMENTAÇÃO E CONTROLE Controle automático de processo Processos Contínuos: são aqueles que possuem saídas contínuas como, por exemplo, processos de geração de energia. Processos
Processos industriais INSTRUMENTAÇÃO E CONTROLE Controle automático de processo Processos Contínuos: são aqueles que possuem saídas contínuas como, por exemplo, processos de geração de energia. Processos
MINISTÉRIO DO TRABALHO E EMPREGO SECRETARIA DE INSPEÇÃO DO TRABALHO DEPARTAMENTO DE SEGURANÇA E SAÚDE NO TRABALHO
 MINISTÉRIO DO TRABALHO E EMPREGO SECRETARIA DE INSPEÇÃO DO TRABALHO DEPARTAMENTO DE SEGURANÇA E SAÚDE NO TRABALHO Trata-se de proposta de texto para revisão do Anexo 8 da Norma Regulamentadora n.º 15 (Atividades
MINISTÉRIO DO TRABALHO E EMPREGO SECRETARIA DE INSPEÇÃO DO TRABALHO DEPARTAMENTO DE SEGURANÇA E SAÚDE NO TRABALHO Trata-se de proposta de texto para revisão do Anexo 8 da Norma Regulamentadora n.º 15 (Atividades
TIC Unidade 2 Base de Dados. Informação é todo o conjunto de dados devidamente ordenados e organizados de forma a terem significado.
 Conceitos relativos à Informação 1. Informação O que á a informação? Informação é todo o conjunto de dados devidamente ordenados e organizados de forma a terem significado. 2. Dados Em informática designa-se
Conceitos relativos à Informação 1. Informação O que á a informação? Informação é todo o conjunto de dados devidamente ordenados e organizados de forma a terem significado. 2. Dados Em informática designa-se
APLICACAÇÃO DE METRICAS E INDICADORES NO MODELO DE REFERENCIA CMMI-Dev NIVEL 2
 APLICACAÇÃO DE METRICAS E INDICADORES NO MODELO DE REFERENCIA CMMI-Dev NIVEL 2 Renan J. Borges 1, Késsia R. C. Marchi 1 1 Universidade Paranaense (UNIPAR) Paranavaí, PR Brasil renanjborges@gmail.com, kessia@unipar.br
APLICACAÇÃO DE METRICAS E INDICADORES NO MODELO DE REFERENCIA CMMI-Dev NIVEL 2 Renan J. Borges 1, Késsia R. C. Marchi 1 1 Universidade Paranaense (UNIPAR) Paranavaí, PR Brasil renanjborges@gmail.com, kessia@unipar.br
Função de Transferência de Malha Fechada
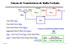 Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
OBJETIVOS: CARGA HORÁRIA MÍNIMA CRONOGRAMA:
 ESTUDO DIRIGIDO COMPONENTE CURRICULAR: Controle de Processos e Instrumentação PROFESSOR: Dorival Rosa Brito ESTUDO DIRIGIDO: Métodos de Determinação de Parâmetros de Processos APRESENTAÇÃO: O rápido desenvolvimento
ESTUDO DIRIGIDO COMPONENTE CURRICULAR: Controle de Processos e Instrumentação PROFESSOR: Dorival Rosa Brito ESTUDO DIRIGIDO: Métodos de Determinação de Parâmetros de Processos APRESENTAÇÃO: O rápido desenvolvimento
1. Introdução. 1.1 Introdução
 1. Introdução 1.1 Introdução O interesse crescente dos físicos na análise do comportamento do mercado financeiro, e em particular na análise das séries temporais econômicas deu origem a uma nova área de
1. Introdução 1.1 Introdução O interesse crescente dos físicos na análise do comportamento do mercado financeiro, e em particular na análise das séries temporais econômicas deu origem a uma nova área de
PRIMAVERA RISK ANALYSIS
 PRIMAVERA RISK ANALYSIS PRINCIPAIS RECURSOS Guia de análise de risco Verificação de programação Risco rápido em modelo Assistente de registro de riscos Registro de riscos Análise de riscos PRINCIPAIS BENEFÍCIOS
PRIMAVERA RISK ANALYSIS PRINCIPAIS RECURSOS Guia de análise de risco Verificação de programação Risco rápido em modelo Assistente de registro de riscos Registro de riscos Análise de riscos PRINCIPAIS BENEFÍCIOS
Principais funções de movimento em analisadores médicos.
 Movimento em analisadores médicos Menor, mais rápido, mais forte. Como os motores em miniatura estão ajudando os equipamentos de diagnóstico a avançar. Os diagnósticos médicos fazem parte da vida cotidiana
Movimento em analisadores médicos Menor, mais rápido, mais forte. Como os motores em miniatura estão ajudando os equipamentos de diagnóstico a avançar. Os diagnósticos médicos fazem parte da vida cotidiana
NÍVEL BÁSICO CAPÍTULO III
 UNIVERSIDADE FEDERAL DO PARÁ CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA ELÉTRICA E DE COMPUTAÇÃO PROGRAMA DE EDUCAÇÃO TUTORIAL SEMANA DOS 40 ANOS DE ENGENHARIA ELÉTRICA NÍVEL BÁSICO CAPÍTULO III PROGRAMA
UNIVERSIDADE FEDERAL DO PARÁ CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA ELÉTRICA E DE COMPUTAÇÃO PROGRAMA DE EDUCAÇÃO TUTORIAL SEMANA DOS 40 ANOS DE ENGENHARIA ELÉTRICA NÍVEL BÁSICO CAPÍTULO III PROGRAMA
SAM GERENCIAMENTO DE ATIVOS DE SOFTWARE
 SAM GERENCIAMENTO DE ATIVOS DE SOFTWARE Modelo de Otimização de SAM Controle, otimize, cresça Em um mercado internacional em constante mudança, as empresas buscam oportunidades de ganhar vantagem competitiva
SAM GERENCIAMENTO DE ATIVOS DE SOFTWARE Modelo de Otimização de SAM Controle, otimize, cresça Em um mercado internacional em constante mudança, as empresas buscam oportunidades de ganhar vantagem competitiva
Sistemas de Controle em Rede
 Sistemas de Controle em Rede Análise, Projeto e Aplicação Prática José C. Geromel FEEC UNICAMP XX CBA 2014 Belo Horizonte, 20-24 de Setembro de 2014 1/53 Conteúdo 1 Introdução 2 Preliminares Planta Controle
Sistemas de Controle em Rede Análise, Projeto e Aplicação Prática José C. Geromel FEEC UNICAMP XX CBA 2014 Belo Horizonte, 20-24 de Setembro de 2014 1/53 Conteúdo 1 Introdução 2 Preliminares Planta Controle
MINISTÉRIO DO TRABALHO E EMPREGO SECRETARIA DE INSPEÇÃO DO TRABALHO DEPARTAMENTO DE SEGURANÇA E SAÚDE NO TRABALHO
 MINISTÉRIO DO TRABALHO E EMPREGO SECRETARIA DE INSPEÇÃO DO TRABALHO DEPARTAMENTO DE SEGURANÇA E SAÚDE NO TRABALHO CONSULTA PÚBLICA do ANEXO 8 da NR-15 PROPOSTA DE TEXTO NORMATIVO NR 15 - ATIVIDADES E OPERAÇÕES
MINISTÉRIO DO TRABALHO E EMPREGO SECRETARIA DE INSPEÇÃO DO TRABALHO DEPARTAMENTO DE SEGURANÇA E SAÚDE NO TRABALHO CONSULTA PÚBLICA do ANEXO 8 da NR-15 PROPOSTA DE TEXTO NORMATIVO NR 15 - ATIVIDADES E OPERAÇÕES
