MINICURSO MINISTRADO NO DINCON 2010 INTRODUÇÃO AOS MÉTODOS PRIMAL-DUAL DE PONTOS INTERIORES E APLICAÇÕES
|
|
|
- Levi Macedo Azambuja
- 8 Há anos
- Visualizações:
Transcrição
1 MINICURSO MINISRDO NO DINCON INRODUÇÃO OS MÉODOS PRIML-DUL DE PONOS INERIORES E PLICÇÕES UORES: Prof. Dr. too Robrto Balbo mal: arbalbo@fc.up Profa. Dra. Eméa Cáa Baptta mal: baptta@fc.up.br Dpartamto Matmátca FC Up Campu Bauru Márco uguto a Slva Soua mal: ma@fc.up.br Mara Cláua Savo Maro clauamaro@hotmal.com Programa Pó-Grauação m Eghara Elétrca FEB UNESP Campu Bauru Up Bauru Março Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
2 . Itroução O problma rtrto O métoo Pala Barrra O métoo pala Dfcula computacoa lgortmo o Métoo Pala O métoo barrra Dfcula computacoa lgortmo o Métoo Barrra Métoo algortmo f Poto Itror lgortmo Prmal fm Iéa Báca o lgortmo Prmal fm lgortmo Prmal fm Implmtao o lgortmo Prmal fm Compla Computacoal O Métoo Dual-fm para o Problma Prmal O lgortmo Dual-fm para o PPL m Formato Prmal O lgortmo Prmal-Dual Poto Itror Iéa báca o lgortmo Prmal Dual Drção Comprmto o Pao Movmto lgortmo Prmal Dual érmo o lgortmo m mpo Polomal Icao o lgortmo Prmal Dual Implmtação Prátca Métoo Prmal Dual para Varáv Caalaa Drçõ Buca Comprmto o Pao Movmto Crtéro Paraa lgortmo Poto Itror Prmal Dual para Varáv Caalaa Varáv Lmtaa Ifrormt O lgortmo Prmal-Dual Poto Itror para Programação Quarátca Cova com varáv caalaa Problma Programação Quarátca Drçõ buca po Prvor Drçõ Buca -po Corrtor Comprmto o pao Crtéro Paraa tualação o parâmtro barrra lgortmo Prmal-Dual para Varáv Caalaa com Procmto Prvor- Corrtor Buca Umoal. PDPCBU O Molo Dpacho Ecoômco PDE plcação ao Molo Dpacho Ecoômco Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
3 7. - aptação o Problma Dpacho Ecoômco ao algortmo propoto PDE com 3 Graor Coraçõ Fa gracmto Bblografa Itroução Em matmátca o trmo otmação ou programação matmátca rfr- ao tuo problma m qu buca mmar ou mamar uma fução atravé a colha tmátca o valor varáv ra ou tra tro um cojuto vávl. m torar algo ótmo é bucar o qu é clt o mlhor poívl "o grau quata ou tao qu cora o ma favorávl m rlação a um trmao crtéro. Otmar é mlhorar até o purmo. No al mlhorar até o mámo. té aqula tuação al a qual como vulgarmt " mr ma pora". Mlhorar ó é poívl tmo colha. Ecolhr uma tr vára altratva. S uma altratva houvr capa trour alguma mlhora fcamo com la. Cao cotráro o qu tmo m mão já é a colha ótma. Otmar é lcoar algo mlhor. Ma qua mpr fcamo rtrto a colhê-lo tr um cojuto lmtao altratva. Obvamt o jo otmar ão bata. Sm crtéro colha por mplo m aata cohcr o uvro altratva. Por outro lao cohco- t ão aata tr crtéro. Iformação portato é fuamtal. Quato ma mlhor; ma pra chgamo à altratva ótma. aplcaçõ a Otmação cotram- prt m toa a moala Eghara a Ecooma a Bologa a grooma tr outra ára tta. Como mplo pomo ctar: Como cortar placa vro forma a atr ao po qu o chgam com um mímo príco poívl matral? Como trbur macat m uma trmaa praa moo qu l trmm ua va o ma prto poívl o poto rgat? Como cotrolar jção combutívl um motor a ploão moo a mamar rmto mmao vbraçõ? Como trbur rga létrca mmao a pra atfao o tma? Como trbur ga létrca mmao o cuto proução atfao o tma? Muto problma pom r molao como problma mamar ou mmar uma fução cuja varáv vm obcr crta rtrçõ:. M mar M amar f ujto a : g m h j j r m ma Ecotrar oluçõ ótma ou mmo apromaa para tpo problma é um afo m mpr fácl r vco. cotrução bo algortmo é a prcpal vocação a otmação. lgortmo gra cofáv qu poívl rolvam cla problma otmação ptmt a mão o parâmtro volvo. t 94 rlatvamt muto pouco tha o volvo obr métoo para otmação umérca muta varáv. maora o métoo otmação foram volvo apó o urgmto o computaor. Durat a Sgua Gra Gurra Mual écaa 4 com o objtvo alocar rcuro cao volvu- o métoo Smpl Datg para problma 3 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
4 lar. O uco crbla gaho urat a gurra foram tão gra qu trmao o coflto grupo ctta a ua ova mtoologa aboragm o problma trafrram para a mpra qu com o "boom" coômco qu guu vram também cofrotaa com problma cão gra compla. aplcação um trmao métoo a um problma ral p bacamt a caractrítca o problma to é o problma r lar ão-lar covo tro âmco tr outra. Em Programação Não-Lar o prmro métoo ram batat rtrto. oraram- gfcatvo o fal a écaa 5 com a troução o métoo métrca varávl por Davo capa olucoar problma muta varáv. Uma cla métoo Otmação muto ploraa o a hoj é omaa métoo Poto tror. O métoo Poto Itror têm o amplamt vtgao utlao prcpalmt a rolução problma Programação Lar ma rctmt m problma Programação Quarátca Não-Lar com bom mpho m problma gra port. a qu ão fom cohco a ltratura com ta omação a tratéga Poto Itror fo troua calmt por FRISCH 955 por CRROL 96 popularaa por FICCO & McCORMICK 968 atravé a utlação a fução Barrra para problma ão-lar. Ralta- qu o tuamo o uo a fução Barrra muu vlmt a écaa 7 vo a algu problma aprtao por ta ta como o mal cocoamto a matr Haa quao u fator Barrra t a ro; a fcula a colha o fator Barrra a colha uma olução cal; a ão-têca a rvaa a olução o aumto lmtao a fução Barrra a vhaça a frotra. O tr pla utlação a mtoologa Poto Itror para a buca oluçõ ótma problma Otmação raparcu quao m 984 KRMRKR 984 publcou o u métoo Projtvo para Programação Lar. Et trabalho provocou uma agtação a atva pqua ta ára. pó a troução fta por Karmarar métoo varat u algortmo orgal foram aprtao. Etr l ctamo: o algortmo Prmal-fm utlao a rolução problma Programação Lar com rtrçõ guala o qual fo aprtao por BRNES 986 por VNDERBEI t al. 986; o algortmo Dual-fm propoto por DLER l al. 989 para rolvr problma Programação Lar a forma guala; a cotrbução MEGIDDO & SHUB 989 com a cação qu a trajtóra qu cou à olução ótma forca plo algortmo f pm a olução cal; a corporação a fução Barrra Logarítmca ao problma Programação Lar a rolução t atravé a mtoologa Poto Itror Prmal-fm Dual- fm o tacamo o trabalho MEGIDDO 987 RENEGR 988 VIDY 99 YE 986; o métoo trajtóra ctral propoto por GONG MONEIRO & DLER 989; o algortmo Prmal-Dual Poto Itror propoto por MONEIRO t al. 99 também por KOJIM t al. 989 o qua ploram uma fução potcal Prmal-Dual varat a fução Barrra Logarítmca o métoo a Barrra Logarítmca Prmal-Dual Prvor-Corrtor m qu a caa tração é ao um pao prvor um pao corrtor trmao rçõ buca mlhor qu a aprtaa por MONEIRO & DLER 989 o qual fo aprtao por MEHROR 99 tr outro. Sguo o avaço o métoo Poto Itror taca- a tora métoo a fução Barrra Mofcaa volva por POLYK 99. Et métoo combam a mlhor propra a fução Lagragaa Cláca a fução Barrra Cláca vtao o problma qu amba frtam. Sguo POLYK 99 a fala qu o métoo a fução Barrra Mofcaa tm para o métoo Poto Itror é a mma qu o métoo a fução Lagragaa umtaa tm para o métoo Pala: ajuá-lo a rblar ua fcula. O métoo a fução Barrra Mofcaa traforma o problma rtrto m um outro problma quvalt o qual é rrtrto rolv uma qüêca problma rrtrto até atgr a olução ótma. Em u trabalho POLYK 99 aprta trê tpo fução Barrra Mofcaa: uma para a fução Barrra CRROL 96 outra para a fução Barrra FRISCH 955 a trcra omaa fução Barrra Shft. Eta fuçõ ão fa atravé a rlaação o cojuto rtrçõ factív. Varat o métoo Barrra Mofcaa pom r cotrao m BREIFELD & SHNNO 996 VSSILIDIS & FLOUDS 997 CHEN & VSSILIDIS 3. 4 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
5 Etõ o métoo Poto Itror para problma ão-lar ão covo ão cotrao m CRPENER t al. 99 VNDERBEI & SHNNO 999 SHNNO & VNDERBEI LUKSN t al. 4 BPIS t al. 6 ab tr outro. É prco tacar qu o métoo Poto Itror têm o utlao para a rolução problma ra a ma vra ára. Nt mcuro aborarmo: o problma rtrto o métoo Pala Barrra o métoo Poto Itror af ro a mtoologa prmal-ual com uma aplcação t métoo ao problma Dpacho Ecoômco BLBO t al..8 tuao a ára Stma Erga m Eghara Elétrca.. O problma rtrto Um problma otmação po r omao rrtrto quao apa uma fução é mmaa ou mamaa tro um cojuto pré-trmao. Matmatcamt rprtamo por: Mmar Mamar f S R m qu R. Quao rtrçõ ão acoaa ao problma. t paa a r omao problma rtrto. Matmatcamt rprtamo por:. o Mmar Mamar f ujto a : g rtrçõ fucoa h S R rtrçõ o cojuto h h h hm R m g g g gp R. r. O problma.. rão clafcao como lar ão-lar quarátco tro covo tr outro acoro com a caractrítca a fuçõ volva. 5 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
6 3. O métoo Pala Barrra O métoo aprtao a gur têm por objtvo rolvr problma programação ãolar rtrto a forma: o: R g Mmar f ujto a: g h m r R h R a fuçõ ão cla C O métoo pala Sguo a éa aocar ao problma 3. uma qüêca problma rrtrto a tratéga o métoo a fução pala cot a utlação uma fução aular o a rtrçõ ão troua a fução objtvo atravé um fator pala o qual pala alguma volação ta. E métoo gra uma qüêca poto factív cujo lmt é a olução ótma o problma orgal. fução aular tm a forma f c P o c omao fator pala P fução pala aocaa a 3. aa por: m P r g hj Θ Λ j 3. o Θ Λ ão fuçõ cotíua uma varávl ta qu: Θ Θ > ; Λ Λ > > fuçõ pom aumr a gut forma: Θ p 3.5 Λ [ma {}] p 3.6 o p é um tro potvo. Para p m a fução P é omaa fução pala quarátca. O problma palao cot m: Mmar { R tal qu θ f c P Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
7 para c. mo qu à ma qu c P a olução o problma palao covrg para a olução o problma orgal. Emplo 3.: Cor o gut problma: M mar ujto a : Ecotrao a fução pala: P M a mar{ } mo qu : θ P c plcao a coçõ otmala: P c c c Fao c tr a fto tmo: Emplo 3.: Cor o gut problma lm c c M mar ujto a : R Rformulao para um problma rrtrto: M mar c.a. R plcao a coção cára ufct para a otmala: 7 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
8 P P c c c c c mo tão qu. Fao c tr a fto: c c c lm lm lm c c c μ c c c 3.. Dfcula computacoa Ecolho- c ufctmt gra a olução o problma palao rá próma à olução o problma 3.; porém para valor muto gra o fator pala trmo alguma problma mal cocoamto. Para valor gra c há uma maor êfa obr a factbla; a maora o métoo otmação rrtrta mov- rapamt a rção um poto factívl. E poto po tar log o ótmo cauao um térmo prmaturo o métoo. Um outro problma é o mal cocoamto a matr Haa vo à ua pêca c. m a aál covrgêca o métoo po fcar prjucaa. Raltamo qu a colha cal o fator pala o parâmtro pala afta a covrgêca o métoo lgortmo o Métoo Pala. Etablcr o rro covrgêca ξ > o poto cal c > o fator crmto a pala β >. o parâmtro pala. Rolvr o problma utlao um métoo mmação rrtrta para μ fo: Mmar f cp R obto tão. < ξ par a olução ótma fo cotraa. São vá para o pao 4 4. Far c βc 5. voltar para o pao. 3. S cp Emplo 3.3: Implmtamo o algortmo a fução utlao o oftar Matlab aplcamo a rolução o problma: M mar ujto a: R 4 8 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
9 So 5 c β a tolrâca o problma prcpal ξ a tolrâca o ub-problma olução por Nto ξ. Utlao o métoo Nto para cotrar o poto ótmo o ubproblma tm-: Itração BEL 3.: Covrgêca o métoo pala c c f θ 45545; ; ; ; ; ; ; ; ; Pomo obrvar qu a caa tração o valor a fução aproma- o valor a fução aular motrao qu o métoo tá covrgo qu a fução pala t a ro. 3. O métoo barrra Da mma forma qu o métoo pala o métoo barrra traformam o problma rtrto m um problma rrtrto. El troum a rtrçõ a fução objtvo atravé um fator barrra qu pala a apromação um poto factívl à frotra a rgão factívl. rabalhao o tror a rgão ta fator gram barrra qu mpm o poto ar la. Logo part- um poto factívl gram- ovo poto factív. Uma a vatag métoo é a obtção plo mo uma olução factívl cao ocorra uma paraa prmatura l. El trabalha omt com problma guala cujo tror é ão-vao. m aum- o problma 3. obco a a coção. Com o objtvo garatr a prmaêca o tror a rgão factívl pomo grar o gut problma barrra: Mmar { f δ B: h < } 3.8 o δ é omao fator barrra B é uma fução barrra ão-gatva cotíua o tror a rgão factívl {; h < } t ao fto à ma qu a olução aproma a frotra a partr o tror. Dfmo tão: r φ B [ h ] o φ é uma fução uma varávl cotíua obr {; < } atfa Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
10 φ < lm φ. 3. fução f δ B é omaa fução aular; a fução barrra po aumr vára forma como: r B ; h r. B l[ h ] fução 3. é omaa barrra cláca ou vra fo tuaa por CRROL 96; 3.6 é omaa fução barrra logarítmca fo tuaa por FRISCH 955. Quao δ B tmo qu δ B aproma a fução barrra al crta atrormt m 3.9 a olução o problma barrra covrg para a olução o problma 3.. Obrvamo qu 3.8 é um problma rtrto po r tão complo quato 3.. Como gmo uma olução cal tror à rgão factívl o métoo trabalha com poto tror a a rgão ao palar o poto qu apromam a frotra mpmo qu l aam a rgão a rtrção po r goraa. rmo ralmt um problma rrtrto para o qual porá r utlaa uma técca otmação rrtrta. Emplo 3.: Rolvr : M mar ujto a: * Obrvamo qu o poto ótmo é ao por f *. Cor tão a fução barrra: B g para δb δ So a fução aular f δb δ tmo o gut problma barrra: Mmar δ < plcao a coçõ otmala: δ δ δ Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
11 δ ± δ Fao δ obtmo F por: δ lm δ δ Not qu à ma qu δ crc h < fto para h. F lm δ F f δ * * δ B aproma uma fução qu tm valor ro para o rolvrmo o problma 3.8 utlao a fução 3. camo o proco olução com um poto tror à rgão factívl. Para caa valor δ tmo uma olução qu rá o poto cal para o proco tratvo. À ma qu δ crc apromamo-o a olução o problma orgal ou ja δ * f δ B f *. 3.. Dfcula computacoa Uma a fcula cotraa o métoo barrra é a lção um poto cal factívl. Em muto problma o po r trabalhoo. Váro métoo pom r utlao para a trmação um poto cal factívl quao t ão é cohco. ambém m vrtu a trutura a fução barrra para valor pquo δ muta técca têm éro problma mal cocoamto rro arroamto quao o ótmo aproma. colha o fator barrra o parâmtro barrra pom compromtr o proco otmação lgortmo o Métoo Barrra. Etablcr o rro covrgêca ξ > o poto cal com g < o parâmtro pala δ > o fator crmto a barrra β.. Uao o métoo Nto rolvr o problma traformao para a forma rrtrta: M mar f δ B ujto a: g < obto tão. 3. S δ B ξ < par a olução ótma fo cotraa. São vá para o pao Far δ βδ 5. voltar para o pao. Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
12 Emplo 3.3: Rolvr o problma abao: ξ a tolrâca o ub- M mar ujto a: So problma olução por Nto ξ. B Itração 4 5 δ β a tolrâca o problma prcpal Nt problma E o problma é rolvo utlao a fução barrra:. Utlao o métoo Nto para cotrar o poto ótmo o ubproblma tm-: δ BEL 3.: Covrgêca o métoo barrra μ f θ B δ 777; ; ; ; ; ; ; ; ; ; ; Pomo obrvar qu a caa tração o valor a fução aproma- o valor a fução aular motrao qu o métoo tá covrgo qu a fução barrra tá to a fto. Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
13 4. Métoo algortmo f Poto Itror 4. - lgortmo Prmal fm Cora- um problma programação lar m ua forma parão Mmar ujto a : b m m qu m R b R R c R o é uma matr poto m. c 4.a 4.b O u problma programação ual é fo por: ma b ujto a: c R m ; c R ; b R m. o 4.ac é chamao Problma Prmal PP 4.c é chamao Problma Dual PD. Obrv qu o omío vávl o problma 4.ab é fo por P { R / b } Df- ma aat o tror rlatvo P com rpto ao paço fm como: P { R / b > } 4. R é chamao um poto tror vávl ou olução tror o problma Um vtor programação lar P. Durat o volvmto t trabalho para garatr a têca poto tror farmo mpr uma upoção fuamtal: P / Há vra mara cotrar uma olução tror um problma programação lar. O talh rão cuto ma tar. Por quato upoha- mplmt qu uma olução tror cal tá poívl aala- a éa báca o algortmo Prmal fm. 4.. Iéa Báca o lgortmo Prmal fm Cora- o prcípo fuamta obrvao por Karmaar a fção u algortmo para a aál o algortmo af ao por: a olução tror atual tvr prto o ctro o poltopo tão fa to movr- uma rção ca rlacoaa ao grat a fução objtvo para cogur um valor mímo; m gra altraçõ o problma orgal uma traformação apropraa po r aplcaa ao paço olução tal qu a olução tror atual ja lvaa para prto o ctro fo o paço traformao. Ø qu: Na formulação Karmarar a trutura pcal mpl fr o poto { R / } ; Δ ta 3 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
14 / / /... / como o poto ctral Δ ta coção fo trmava o poto troua propotaamt obco o prcípo upractao. Quao trabalha rtamt o problma a forma parão a trutura mpl aotaa por Karmarar tá log r cogua o omío vávl pora traformar- um cojuto polral lmtao. oa a trutura a r obca pla formatação parão cot a trção o paço{ R / b} formao pla rtrçõ plícta com o cojuto fo plo octat potvo{ R / } rquro pla rtrçõ ão-gatva. É óbvo qu o octat ão-gatvo ão tm um poto "ctral" ral. Etrtato atravé alguma traformação fta cogur pocoar o ctro o poto... ao mo cogurá matr- a uma tâca gual caa fac o octat ão-gatvo. Ito ocorr qu a tâca movmto qualqur poto qu mov o poto ctral é mpr mor qu prmac o tror o octat ão gatvo. Coqütmt purmo cotrar uma traformação apropraa qu trac uma olução tror atual ao poto tão aalogamt ao algortmo traformação projtva Karmarar pomo car uma tratéga mofcaa como gu: "umo uma olução tror aplqu uma traformação apropraa ao paço oluçõ tal forma a colocar a olução corrt m o paço traformao tão camh a rção ca máma o paço ulo úclo a matr a rtrçõ plícta traformaa ma cotrolao o tamaho o pao rlatvo à rtrçõ ão-gatva a fm prmacr m uma olução tror o paço traformao. Etão ama- a traformação vra para traçar potrormt a olução cotraa ao paço olução orgal como uma ova olução tror. Rpt- t proco até a otmala ou quao a coçõ paraa form atfta." Uma traformação apropraa t cao fo aqula omaa traformação fm. partr ta o pquaor omaram o algortmo varat ta traformação com algortmo af. Quao a traformação é aplcaa rtamt ao problma prmal a forma parão oma- algortmo Prmal fm. E para o problma o formato ual algortmo Dual fm. raformação afm o octat ão gatvo. Sja R um poto tror o octat ão gatvo R to é > para... Dfrmo uma matr agoal R por: 4.3 ag Not qu a matr é ão gular amt uma matr vra qu é também uma matr agoal ma com / como u -émo lmto agoal para.... traformação afm é fa o octat ão gatvo 4 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN R por R R : tal qu: 4.4 traformação 4.4 mplmt rcala a -éma compot por um úmro potvo. Gomtrcamt la traforma poto gmto rta o paço orgal para poto gmto rta o paço traformao. Daí a omação traformação fm. Fgura 4. lutra o boço gométrco a traformação o paço bmoal. Not qu para o cao a rtrçõ bmoa guala rprtaa a fgura 4. a varáv calaa clum a
15 varáv folga também. D fato caa bora o polígoo corrpo a uma varávl folga qu tá o ajutaa m ro. Etrtato é fícl rprtar o boço complto uma mma fgura. FIGUR 4. - Eboço gométrco a traformação fm o paço bmoal gut propra K po- faclmt rm vrfcaa: é uma aplcação bm fa é um poto tror o tão 3 é um vértc R. 4 tá a frotra o octat 5 é um poto tror 6 qu: R a R for um vértc. R R for um poto a frotra. R for um poto tror. é uma traformação buívoca a qual amt uma traformação for um poto tror vra R tal para caa R 4.5 Supoha qu uma olução tror o problma programação lar 4.ab é aa. Po aplcar a traformação afm para "ctrar" ua magm m. Pla rlação motraa m 4.5 o paço olução traformao tm- um problma programação lar corrpot a: Mmar c 4.6a ujto a : b 4.6b o c c. No problma 4.6 a magm to é tora- qu matêm a tâca utára a frotra fa o octat ão-gatvo. S movrmo ao logo uma rção qu cotr o paço ulo a matr com um comprmto pao aproprao α > tão o ovo poto α prmac tror vávl para o problma 4.6. lém 5 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
16 o ua magm vra tora- uma ova olução tror para o problma 4.ab. D qu oo objtvoo é mmar o valor a fução objtvo a tratéga aotar o procmto máma ca é caa. Ou ja qur- projtar o grat gatvo c o paço ulo a matr crar uma rção factívl qu mlhora ou mu a fução objtvo o paço traformao. Para t fm f- prmramt a matr ula a projção o paço por: P I I 4.7 Etão a rção movmto é aa por: P c [ I ] c Not qu a matr projção P é bm fa ao logo mpr qu complto m >. É tambémm fácl vrfcar qu. Fgura. motra projção. 4.8 u tm poto a o boço a FIGUR 4. Eboço a projçãoo o vtor rção o Métoo Prmal fm o paço bmoal gora tm- a coção muar o paço olução traformao a olução tror atual ao logo a rção para uma ova olução tror > garato o crécmo o valor a fução objtvo. Fao am tm- qu colhr um comprmto o pao α > aproprao tal qu: α Obrv qu tão α porá r colho como qualqur úmro potvo prmaco o tror a rgão.. Not qu < para algum tão α v r colho calmt corao a raõ: > Dta forma po- colhr < α < aplcar o tt rao mímo α m α < ; 6 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
17 para trmar um comprmto o pao aproprao qu garata a potva. Quao α tá prto a olução atual é mova qua mpr para a frotra ma próma o octat potvo para fr uma ova olução tror o paço traformao. Eta muaça olução é lutraa também a fgura 4.. Noa próma tarfa é traformar a ova olução para o paço olução orgal para obtr uma olução mlhoraa para o problma 4.ab. Ito porá r fto aplcao a traformação vra a. Em outra palavra tm-: o α α P c α I 7 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN [ ] c [ c c] [ c ] α α 4. c 4. Ito gfca qu a rção movmto o paço olução orgal é [ c ] α quao [ c ] o paço traformao. Dvra o comprmto o pao é obrvaçõ mportat pom r fta aqu: Obrvação. Not qu PK c vta m 4.7. O crécmo a fução objtvo é motrao a partr : c c o α c c α c α α c P é uma matr projção c 4. Ito mplca qu é crtamt uma olução crécmo a fução objtvo a rção movmto. lém o têm- o gut lma qu pom r cotrao m [FNG PUHENPUR 993]: Lma 4.. S tr um 4.ab é lmtao. Prova. D qu α P com > tá o paço ulo a matr rtrção α tão o problma programação lar > ab- qu é vávl ao problma 4.6 para too >. Coqutmt po- colhr α o ftamt potvo tão a Equação 4. mplca qu o lmt c aproma t caopara α P. Lma 4.. S t um P com tão toa olução vávl o problma programação lar 4.ab é ótma.
18 ab qu Prova. Rcor qu P é uma matr projção o paço ulo. Para P c c tá o complmto ortogoal o paço ulo a matr ortogoal t cao é o paço fo plo úmro lha a matr qu. D qu o complmto t um vtor u c ou u c D qu t gu qu u c. gora para toa a olução vávl c u u b D qu u b ão p o valor c prmac cotat m P. u tal Lma 4.3. S o problma programação lar 4.ab for frormt lmtao ua fução objtvo ão for cotat tão a qüêca { c...} é bm fa trtamt crct. Prova. Eta é uma coqüêca rta o Lma Equação 4.. Obrvação. S for ralmt um poto o vértc tão a prão 4. po r rua a B cb o qual é fo como o " vtor Dual" para o Métoo Dual Smpl. m oma- como tmaor ual corrpot à olução prmal o algortmo Prmal fm. lém o t cao o vtor: r c 4.3 ru- a c B cb qu é o cohco vtor cuto ruo ou cuto rlatvo o Métoo Smpl. Daí chama- r vtor cuto ruo ou rlatvo aocao a o algortmo afm. Obrv qu quao r a tmatva ual traforma uma olução vávl ual r r traforma a folga complmtar o par olução vávl to é c b r 4.4 No cao r com r tm- coguo tão a factbla prmal a factbla ual a coçõ folga complmtar. Ou ja é ótmo prmal é ótmo ual. Baao a cuão acma boça- aqu um procmto tratvo o algortmo Prmal fm. 4.. lgortmo Prmal fm. Pao calação: Etablcmo > tal qu b cuto ma tar. Dtalh a r Pao Cálculo o vtor tmatva ual: Calcular o vtor tmatva Dual. c o é a matr agoal vto m 4.3 cujo lmto ão a compot. Pao 3 Cálculo o vtor cuto rlatvo: Calcular o vtor cuto ruo. r c 8 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
19 Pao 4 t para otmala: S r r ε um úmro potvo pquo fo tão PRE gut. é ótmo prmal Pao 5 Drção tralação: Calcul a rção r 9 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN é ótmo ual. Cao cotráro vá para o pao Pao 6 t para lmtara valor objtvo cotat: S > tão PRE o problma é lmtao. S tão também PRE para o Pao 7. é ótmo prmal. Cao cotráro vá Pao 7 Cálculo o comprmto o pao: Calcul o comprmto o pao α α m tal qu < Pao 8 Dtrmação uma ova olução: tual Faça vá para o pao α o < α < O lgortmo Prmal fm vto ta ção mplmtao m Lguagm Pacal 7. é utlao o mplo umérco 4. ao a gur para lutrar t algortmo Emplo 4. Cora- o Problma Programação Lar: Mmar - ujto a : 5 5 Et a forma caôca é pro por: Mmar - ujto a : O métoo Prmal fm rá ttao para o problma ao a forma caôca ou ja o problma 4.. a qual tá fo com rtrçõ guala. Nt cao - B [ 5 5] c [- ] um- [ 7 3] a qual é uma olução tror factívl. Daí: 7 lém o 3 c [ ]
20 [ ] r c 77 D qu alguma compot r ão gatva r. 87 olução atual é ão ótma. Coqütmt progu- para ttar a rção buca com r [ ] Supoha qu é colho α. 99 tão o comprmto o pao.99 α Coqütmt a ova olução é: o α [ ] Obrv qu o valor a fução objtvo fo mlhoraa 8 ab- qu a para Fao- ma traçõ vrfca- qu o proco tratvo covrg à olução ótma [ ] com o valor a fução objtvo 45. O rultao obto a trprtação gométrca o problma ao a oluçõ cotraa plo algortmo ão vta rpctvamt a abla 4. a Fgura 4.3. BEL 4. Rultao Obto plo lgortmo Prmal fm para o 4.. Itração Fução Objtvo Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
21 olução ótma cotraa computacoalmt fo o valor a fução objtvo é Na mplmtação fta o algortmo Prmal fm ão fo utlao como crtéro paraa o crtéro a folga complmtar. Nta optou- por utlar o crtéro mpl m compot trm a ro o qu trma um vértc o problma para uma prcão ε 3. FIGUR 4.3 Itrprtação gométrca para o problma.4.a a oluçõ obta plo algortmo Prmal fm covrgêca o algortmo Prmal fm. Noo objtvo é motrar qu a qüêca { } graa plo algortmo Prmal fm m parar a tapa 6 covrg a uma olução ótma o problma programação lar 4.ab. fm mplfcar a prova fa- a gut upoçõ:. O problma programação lar m coração tm um omío vávl lmtao com tror ão-vao;. O problma programação lar é ão-grao prmal ão grao ual. prmra upoção rtra a pobla trmar o algortmo Prmal fm com lmtara po r potrormt motrao qu ta ua upoçõ mplcam qu: ' a matr é poto complto m colua L.I. para caa P ; m o vtor tmaor ual r têm o mámo m ro para caa R. gur rão rvto algu Lma mpl ma mportat para oa aál covrgêca. Lma Quao aplca- o algortmo Prmal fm tm- qu lm r. Prova. D qu a qüêca { c K } é mootocamt crct é lmtaa frormt pla prmra upoção tão a mma é covrgt. Daí a quaçõ mplcam qu Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
22 lm c c lmα lm α Obrv qu α > logo tm-: lm lm r E a prova o rultao é mata. Not qu o rultao acma é atamt a coção a folga complmtar. Dfo C P como o o cojuto m qu vrfcam a folga complmtar ou ja: C { P / r } ; 4.5 além o trouo D P como o o cojuto m qu a coção vávl ual vrfca to é D { P / r } ; 4.6 corao- a coçõ otmala o problma programação lar é fácl provar o gut rultao: C D Lma Para too é uma olução ótma o problma programação lar 4.ab. gora tá- proto para provar qu a qüêca { } graa plo algortmo Prmal fm covrg para uma olução ótma o problma 4.. Prmramt motra- qu: 4.ab orma 4. - S { } covrgr tão lm é uma olução ótma para problma Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN Prova Prova- t rultao pla cotração. Prmramt ot qu quao { K } covrgr para ão é ótmo prmal. D qu. lém o o Lma 4.4 mplca qu: v r vávl prmal. Etrtato para provar t rultao aum- qu r é uma fução cotíua a r lm r ab- qu r lm r é bm fo. Daí tm- C. Por upoção Lma 4.5 ab- qu D. Coqutmt t ao mo um íc j tal qu r j <. Rcorao qu C tm- j. Dvo à cotua r t um tro K tal qu para too K { } <. Etrtato cor qu: j j D qu r < j j j j j r j α j r j tmo > > K. Daí chga- a uma cotração oa hpót. Portato O trabalho rtat v motrar qu a qüêca { } crtamt covrg. j o qu cotra o fato qu é ótmo prmal.
23 orma 4. - qüêca { } graa plo algortmo Prmal fm é covrgt. Prova. D qu o omío vávl é ão-vao fchao lmtao vo a compaca o cojuto P a qüêca { } tm ao mo um poto acumulação m P to. Noo objtvo é motrar qu { }. é também o úco poto acumulação { } Obrvao- qu r. é uma fução cotíua m aí t é o lmt a qüêca graa aplcao- o Lma 4.4 po- coclur qu C. lém o a upoção ão-gração mplca qu caa lmto m C cluo v r uma olução vávl báca vértc P. Daí pomo otar ua varáv ão báca por f- Ñ como o íc para ajutar ta varáv ão báca. lém o j para too δ > f- uma bola rao δ > ao ror Bδ { P / < δ N } aa por : um- qu r ja o vtor cuto ruo corrpot a ual agura-o cotrar um ε > tal qu m r ~ j N j > ε. ão gração prmal Rcor qu a upoção ão-gração mplca m caa mmbro C r um vértc P há omt um úmro fto o vértc m P. Daí C tm um úmro fto lmto po- colhr um aproprao δ > tal qu B δ C 4.7a m > 4.7b Rcorao qu tm- ~ j N lm K r j ε B δ lm lm[ r ] K j j Dvo à coção P r lmtao ab- qu o comprmto o pao α m caa tração é um úmro potvo lmtao. Coqütmt para ε δ apropraamt colho B δ qu é ufctmt prómo vê- qu α [ j rj ] < ε δ. Daí po- fr um cojuto ~ Sε δ { B α [ j rj ] < ε δ j N} 4.8 gora para too Sε δ 4.8 mplca qu ~ α [ j ] rj < δ j N qu além o ~ j j α [ j rj ] < δ j N Ito motra qu B S j δ ε r 3 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
24 gora po- motrar qu é o úco poto acumulação { K } upõ- qu a qüêca { } tm ma um poto acumulação. D qu. Por cotração é um poto acumulação a qüêca { } prtc a S ε δ mpr qu 4.7b tá atfta. Ma como ão é o úco poto acumulação a qüêca é altraa mpr qu aproma um ovo poto atfa 4.7b. Etrtato caa v qu a qüêca é altraa S ε δ la prmac m B δ / Sε δ. Coqütmt fto lmto { } prmacm m B δ / Sε δ. Not qu t frt cojuto tm um fcho compacto a ubqüêca { } qu prtc a B δ / Sε δ v tr um poto acumulação o fcho compacto. Dvo à fção C ab- qu caa poto acumulação { } v prtcr-lh. Etrtato C é juto o fcho B δ / Sε δ. Et fato juto com a Equação 4.7 caua uma cotração. m crtamt é o lmt a qüêca { }. Ma rultao a rpto a covrgêca o algortmo fm ob a coção gração tm aparco rctmt Implmtao o lgortmo Prmal fm mplmtaçõ fta ctam um poto tror cal para rm aplcaa. Nta ção rá fo um procmto para trmação uma olução factívl cal bm como a vrfcação a ocorrêca otmala a buca uma olução báca vávl báca ótma. Icao o algortmo Prmal fm. D mara aáloga aqula tablca para o Métoo Smpl Rvao [LUENBERGER 984] rá trouo aqu o mcamo a abr o Métoo Bg-M o Métoo Dua-Fa para cotrar uma olução vávl tror cal. O prmro métoo é cutao ma faclmt aproprao para a maora a aplcaçõ. Etrtato uma cução comrcal ma éra cora frqütmt o guo métoo vo a ua tabla. a Métoo Bg-M. Nt métoo acoa- uma varávl artfcal aocao com um úmro potvo gra M ao programa lar orgal para far qu... R traform uma olução vávl tror cal para o gut problma: a Mmar c M 4.9a a ujto a : [ b ] b 4.9b a o... R. Comparao o Métoo Bg-M com o Métoo Smpl Rvao tm- aqu omt varáv m v m. Quao o algortmo Prmal fm é aplcao ao problma Bg-M 4.9ab com M ufctmt gra qu o problma ja vávl chga- m uma olução ótma ao problma Bg-M ou coclu- qu o problma é lmtao. S a varávl artfcal prmacr potva a a olução fal o problma Bg-M tão o problma programação lar orgal é factívl. Cao cotráro ou o problma orgal é frormt lmtao ou é a olução ótma o problma programação lar orgal. pó a coraçõ o mcamo ca vê- o crtéro paraa para a mplmtação o algortmo Prmal fm. orma.3.: Coçõ Otmala Karuh-Kuh-ucr - KK * é uma olução Cor o problma 4.ab o problma o formato ual 4.c. O vtor é olução ótma para o Problma Dual 4.c omt : b factbla prmal ótma o problma 4.ab * * 4 Procg of th 9th Brala Cofrc o Damc Cotrol a thr pplcato Srra Ngra SP - ISSN
IND 1115 Inferência Estatística Semestre turma B Teste 2 10/06/2005 GABARITO
 IND 5 Ifrêca statístca Smstr 5. turma B Tst /6/5 GABARITO PROBLMA ( potos m caa qustão abao, qu s a afrmatva é vrara ou falsa (marqu um a altratva corrta. Não é cssáro justfcar a sua rsposta. Vraro Falso
IND 5 Ifrêca statístca Smstr 5. turma B Tst /6/5 GABARITO PROBLMA ( potos m caa qustão abao, qu s a afrmatva é vrara ou falsa (marqu um a altratva corrta. Não é cssáro justfcar a sua rsposta. Vraro Falso
( )( ) ( ) 2 2 ( ) ( ) 2. Questões tipo exame. Pág θ =. θ =, logo. Portanto, 1.1. ( ) 2. = θ 4.º Q, ou. = θ, tem-se.
 + 8...... Sdo Arg( ) θ, tm-s sja, taθ θ.º quadrat, tão Portato,. Pág. 8 taθ θ.º Q, ou θ. + + b ( + ) + b( + ) + c b c + + + + c + + + b b c b+ b+ c ( b ) b+ c+ b+ c b c + b b c b Portato, b c.. + S Arg(
+ 8...... Sdo Arg( ) θ, tm-s sja, taθ θ.º quadrat, tão Portato,. Pág. 8 taθ θ.º Q, ou θ. + + b ( + ) + b( + ) + c b c + + + + c + + + b b c b+ b+ c ( b ) b+ c+ b+ c b c + b b c b Portato, b c.. + S Arg(
CAPÍTULO 3 TÉCNICAS USADAS NA DISCRETIZAÇÃO. capítulo ver-se-á como obter um sistema digital controlado através de técnicas
 3 CAPÍTULO 3 TÉCNICAS USADAS NA DISCRETIZAÇÃO A técnca uada para obtr um tma dgtal controlado nctam, bacamnt, da aplcação d algum método d dcrtação. Matmatcamnt falando, pod- obrvar qu o método d dcrtação
3 CAPÍTULO 3 TÉCNICAS USADAS NA DISCRETIZAÇÃO A técnca uada para obtr um tma dgtal controlado nctam, bacamnt, da aplcação d algum método d dcrtação. Matmatcamnt falando, pod- obrvar qu o método d dcrtação
Capítulo 8. (d) 1) 0,5 2) 1,0 3) 0,5 4) 0 5) 2/3 6) 1/2. Problema 02. (a) (b)
 Capítulo Problma. Ω{C C C C C5 C R R R R R5 R} Od: Ccara Rcoroa 5 P 5 5 P 7 7 7 7 7 7 c Sm pos P j P P j j d 5 5 5 / / Problma. P 5 P 5 9 5 7 9 c Não pos P P P 9 d P / P / 5 P 5 P 5 Problma. Prchdo os
Capítulo Problma. Ω{C C C C C5 C R R R R R5 R} Od: Ccara Rcoroa 5 P 5 5 P 7 7 7 7 7 7 c Sm pos P j P P j j d 5 5 5 / / Problma. P 5 P 5 9 5 7 9 c Não pos P P P 9 d P / P / 5 P 5 P 5 Problma. Prchdo os
C. Almeida (1987) Determinação da transmissividade e coeficiente de armazenamento por ensaios de recuperação
 C. Almda (1987 Dtrmação da tramvdad cofct d armazamto or ao d rcuração Hdrogologa y Rcuro Hdráulco, t. XII,. 689-694. IV IMPOIO DE HIDROGEOLOGÍA ALMEIDA, Carlo DEERMINAÇÃO DE RANMIIVIDADE E COEFICIENE
C. Almda (1987 Dtrmação da tramvdad cofct d armazamto or ao d rcuração Hdrogologa y Rcuro Hdráulco, t. XII,. 689-694. IV IMPOIO DE HIDROGEOLOGÍA ALMEIDA, Carlo DEERMINAÇÃO DE RANMIIVIDADE E COEFICIENE
4. VIBRAÇÃO FORÇADA - FORÇAS NÃO SENOIDAIS
 VIBRAÇÕES MEÂNIAS - APÍTULO VIBRAÇÃO ORÇADA 3. VIBRAÇÃO ORÇADA - ORÇAS NÃO SENOIDAIS No capíulo ao suou-s a vbação oçaa ssas co u gau lba, subos a oças cação oa soal. Es suo po s so paa aplcaçõs quao as
VIBRAÇÕES MEÂNIAS - APÍTULO VIBRAÇÃO ORÇADA 3. VIBRAÇÃO ORÇADA - ORÇAS NÃO SENOIDAIS No capíulo ao suou-s a vbação oçaa ssas co u gau lba, subos a oças cação oa soal. Es suo po s so paa aplcaçõs quao as
Capitulo 5 Resolução de Exercícios
 Captulo 5 Rsolução Exrcícos FORMULÁRIO Dscoto Racoal Smpls D ; D ; ; D R R R R R R Dscoto Comrcal Smpls D ; ; D C C C C Dscoto Bacáro Smpls D s ; s ; D b b b b s Db ; b Rlaçõs tr o Dscoto Racoal Smpls
Captulo 5 Rsolução Exrcícos FORMULÁRIO Dscoto Racoal Smpls D ; D ; ; D R R R R R R Dscoto Comrcal Smpls D ; ; D C C C C Dscoto Bacáro Smpls D s ; s ; D b b b b s Db ; b Rlaçõs tr o Dscoto Racoal Smpls
Métodos Numéricos para a Solução de Problemas de Valor de Contorno
 Métoo Nmérco ara a Soção robma Vaor Cotoro Eqaçõ rca orára Emo. Dão-ração m ma artíca cataítca oroa: R Fgra. artíca cataítca érca. Baaço maa: tao tacoáro otérmco C Dr r r r r < r < R C r r mtra CR C o
Métoo Nmérco ara a Soção robma Vaor Cotoro Eqaçõ rca orára Emo. Dão-ração m ma artíca cataítca oroa: R Fgra. artíca cataítca érca. Baaço maa: tao tacoáro otérmco C Dr r r r r < r < R C r r mtra CR C o
Exercícios de Cálculo Numérico Interpolação Polinomial e Método dos Mínimos Quadrados
 Eercícos e Cálculo Numérco Iterpolação Polomal e Métoo os Mímos Quaraos Para a ução aa, seja,, 6 e, 9 Costrua polômos e grau, para apromar, 5, e ecotre o valor o erro veraero a cos b c l Use o Teorema
Eercícos e Cálculo Numérco Iterpolação Polomal e Métoo os Mímos Quaraos Para a ução aa, seja,, 6 e, 9 Costrua polômos e grau, para apromar, 5, e ecotre o valor o erro veraero a cos b c l Use o Teorema
Universidade Salvador UNIFACS Cursos de Engenharia Métodos Matemáticos Aplicados / Cálculo Avançado / Cálculo IV Profa: Ilka Rebouças Freire
 Univridad Salvador UNIFACS Curo d Engnharia Método Matmático Alicado / Cálculo Avançado / Cálculo IV Profa: Ilka Rbouça Frir A Tranformada d Lalac Txto 3: Dlocamnto obr o ixo t. A Função Dgrau Unitário.
Univridad Salvador UNIFACS Curo d Engnharia Método Matmático Alicado / Cálculo Avançado / Cálculo IV Profa: Ilka Rbouça Frir A Tranformada d Lalac Txto 3: Dlocamnto obr o ixo t. A Função Dgrau Unitário.
Sistema de Detecção, Localização e Isolamento de Ramos com Vazamento em Redes de Gás Natural
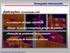 Stma Dtcção, ocalzação Iolamnto Ramo com Vazamnto m R Gá Natural Joé Wanrly Scucugla lo orra Souza rtan Mara M. M. Patríco Núclo Enrga, Automação ontrol NEA, UNIDERP, Rua rará, 900-00, ampo Gran, MS E-mal:
Stma Dtcção, ocalzação Iolamnto Ramo com Vazamnto m R Gá Natural Joé Wanrly Scucugla lo orra Souza rtan Mara M. M. Patríco Núclo Enrga, Automação ontrol NEA, UNIDERP, Rua rará, 900-00, ampo Gran, MS E-mal:
Leonardo da Vinci ( ), artista, engenheiro e cientista italiano
 ormas dos rabalhos Vrtuas Itrodução Loardo da Vc (45-59), artsta, ghro ctsta talao Aplcou oçõs do prcípo dos dslocamtos vrtuas para aalsar o qulíbro d sstmas d polas alavacas PEF-40 Prof. João Cyro Adré
ormas dos rabalhos Vrtuas Itrodução Loardo da Vc (45-59), artsta, ghro ctsta talao Aplcou oçõs do prcípo dos dslocamtos vrtuas para aalsar o qulíbro d sstmas d polas alavacas PEF-40 Prof. João Cyro Adré
Transistor Bipolar de Junção TBJ Cap. 4 Sedra/Smith Cap. 8 Boylestad Cap. 11 Malvino
 Trantor Bpolar d Junção TBJ Cap. 4 Sdra/Smth Cap. 8 Boyltad Cap. 11 Malno Amplfcador BC CC Nota d Aula SEL 313 Crcuto Eltrônco 1 Part 7 1 o Sm/216 Prof. Manol Amplfcador m Ba-Comum ( BC ) Nta confguração,
Trantor Bpolar d Junção TBJ Cap. 4 Sdra/Smth Cap. 8 Boyltad Cap. 11 Malno Amplfcador BC CC Nota d Aula SEL 313 Crcuto Eltrônco 1 Part 7 1 o Sm/216 Prof. Manol Amplfcador m Ba-Comum ( BC ) Nta confguração,
A B LM. A onde Y Y ; P. P P, no PONTO. T o que provocará um C 0. T 0 desloca curva IS para a direita IS IS
 Gabarto Blachard Capítulo 7 2) Choqu d gasto médo prazo MODELO AD AS (OA-DA) Rdução do Imposto d Rda (T): C c c T 0 0 c 0 - cosumo autôomo c - propsão margal a cosumr T 0 dsloca curva IS para a drta Dado
Gabarto Blachard Capítulo 7 2) Choqu d gasto médo prazo MODELO AD AS (OA-DA) Rdução do Imposto d Rda (T): C c c T 0 0 c 0 - cosumo autôomo c - propsão margal a cosumr T 0 dsloca curva IS para a drta Dado
Tópicos Especiais em Energia Elétrica (Projeto de Inversores e Conversores CC-CC)
 partamnto Engnhara Elétra Tópo Epa m Enrga Elétra Projto nror onror - Aula 3. Molagm o onror: Molo a ha PWM Prof. João Améro lla Bblografa HAT,. W. Eltrôna Potêna - Anál Projto ruto. AMGH Etora TA, 23.
partamnto Engnhara Elétra Tópo Epa m Enrga Elétra Projto nror onror - Aula 3. Molagm o onror: Molo a ha PWM Prof. João Améro lla Bblografa HAT,. W. Eltrôna Potêna - Anál Projto ruto. AMGH Etora TA, 23.
TÓPICOS. Teoria dos residuos. Classificação de singularidades. Teorema dos resíduos.
 Not bm a ltura dsts apotamtos ão dspsa d modo algum a ltura atta da bblograa prcpal da cadra hama-s à atção para a mportâca do trabalho pssoal a ralar plo aluo rsolvdo os problmas aprstados a bblograa
Not bm a ltura dsts apotamtos ão dspsa d modo algum a ltura atta da bblograa prcpal da cadra hama-s à atção para a mportâca do trabalho pssoal a ralar plo aluo rsolvdo os problmas aprstados a bblograa
Curso: Engenharia Industrial Elétrica. Análise de variáveis Complexas MAT 216 Turma: 01
 urso: Egharia Idustrial Elétrica Aális d variávis omplas MAT 6 Profssora: Edmary S B Araújo Turma: Lista d Provas Rspodu Jsus: Em vrdad, m vrdad t digo: qum ão ascr da água do Espírito ão pod trar o rio
urso: Egharia Idustrial Elétrica Aális d variávis omplas MAT 6 Profssora: Edmary S B Araújo Turma: Lista d Provas Rspodu Jsus: Em vrdad, m vrdad t digo: qum ão ascr da água do Espírito ão pod trar o rio
Com muito carinho para minha querida amiga e super profissional. Ale Del Vecchio
 Com muito carinho para minha querida amiga e super profissional. BA BE BI BO BU BÃO ba be bi bo bu bão BA ba boi BE be bebê BI bi Bia BO bo boi BU bu buá Nome: BA BE BI BO BU BÃO ba be bi bo bu bão BA
Com muito carinho para minha querida amiga e super profissional. BA BE BI BO BU BÃO ba be bi bo bu bão BA ba boi BE be bebê BI bi Bia BO bo boi BU bu buá Nome: BA BE BI BO BU BÃO ba be bi bo bu bão BA
Um Modelo de Compressão de Imagens Digitais Baseado em Codificação Fractal e Quantização Vetorial (VQ)
 Um Molo Comprssão Imags Dgtas Basao m Cofcação Fractal Quatzação Vtoral (VQ) João Paulo I. F. Rbas Uvrsa Fral Ubrlâa Dpartamto Eghara Elétrca Ubrlâa-MG, Brasl joaorbas@gmal.com Glbrto A. Carrjo Uvrsa Fral
Um Molo Comprssão Imags Dgtas Basao m Cofcação Fractal Quatzação Vtoral (VQ) João Paulo I. F. Rbas Uvrsa Fral Ubrlâa Dpartamto Eghara Elétrca Ubrlâa-MG, Brasl joaorbas@gmal.com Glbrto A. Carrjo Uvrsa Fral
Texto para Coluna do NRE-POLI na Revista Construção e Mercado Pini - Novembro 2013
 Txto para Coluna do NRE-POLI na Rvita Contrução Mrcado Pini - Novmbro 2013 Rico do Tomador do Agnt Financiro no Uo do Sitma Pric m rlação ao Sitma SAC no Financiamnto d Imóvi Ridnciai Prof. Dr. Claudio
Txto para Coluna do NRE-POLI na Rvita Contrução Mrcado Pini - Novmbro 2013 Rico do Tomador do Agnt Financiro no Uo do Sitma Pric m rlação ao Sitma SAC no Financiamnto d Imóvi Ridnciai Prof. Dr. Claudio
/ d0) e economicamente (descrevendo a cadeia de causação
 UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DEPARTAMENTO DE ECONOMIA EAE 26 Macroconoma I º Smstr 27 Profssor Frnano Rugtsky Lsta Exrcícos [] Consr uma macroconoma scrta
UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DEPARTAMENTO DE ECONOMIA EAE 26 Macroconoma I º Smstr 27 Profssor Frnano Rugtsky Lsta Exrcícos [] Consr uma macroconoma scrta
Anexo III Temperatura equivalente de ruído, Figura de ruído e Fator de mérito para estações de recepção (G/T)
 Axo III mpratura quivalt d ruído, igura d ruído ator d mérito para staçõs d rcpção (/) III.. mpratura Equivalt d Ruído A tmpratura quivalt d ruído d um compot pod sr dfiida como sdo o valor d tmpratura
Axo III mpratura quivalt d ruído, igura d ruído ator d mérito para staçõs d rcpção (/) III.. mpratura Equivalt d Ruído A tmpratura quivalt d ruído d um compot pod sr dfiida como sdo o valor d tmpratura
Análise de Processos ENG 514
 áli d Proco NG 54 apítulo 5 Modlo do Tipo trada-saída Pro. Édlr Li d lbuqurqu Julho d 4 Forma d Rprtação d Modlo Matmático Fomológico Modlo dcrito por quaçõ Dirciai Modlo a orma d paço d tado Modlo do
áli d Proco NG 54 apítulo 5 Modlo do Tipo trada-saída Pro. Édlr Li d lbuqurqu Julho d 4 Forma d Rprtação d Modlo Matmático Fomológico Modlo dcrito por quaçõ Dirciai Modlo a orma d paço d tado Modlo do
MATEMÁTICA. 01. Sejam os conjuntos P 1, P 2, S 1 e S 2 tais que (P 2 S 1) P 1, (P 1 S 2) P 2 e (S 1 S 2) (P 1 P 2). Demonstre que (S 1 S 2) (P 1 P 2).
 GGE RESOE - VESTIBULAR IME MATEMÁTICA) MATEMÁTICA Sj o ojuo S S qu S ) S ) S S ) ) or qu S S ) ) : Sj S S Coo S S ão ou l r o rol oo uor r grl) qu oo S ão logo oo qurío orr F F F F F ) Crufrê ro -) ro
GGE RESOE - VESTIBULAR IME MATEMÁTICA) MATEMÁTICA Sj o ojuo S S qu S ) S ) S S ) ) or qu S S ) ) : Sj S S Coo S S ão ou l r o rol oo uor r grl) qu oo S ão logo oo qurío orr F F F F F ) Crufrê ro -) ro
Medley Forró 4 Tenho Sede Dominguinhos e Anastácia
 TENOR Medley Forró 4 Tenho Sede Dominguinhos e Anastácia q # = 0 # # 4 # c. # n 8. iá. Lá lá lá iá lá iá lá lá iá lá iá lá iá lá iá... A iá Tra -ga me'um co - po dá - gua gan ta pe de'um pou te - nho -
TENOR Medley Forró 4 Tenho Sede Dominguinhos e Anastácia q # = 0 # # 4 # c. # n 8. iá. Lá lá lá iá lá iá lá lá iá lá iá lá iá lá iá... A iá Tra -ga me'um co - po dá - gua gan ta pe de'um pou te - nho -
Análise de Sistemas Lineares
 nál Sma Lnar Dnvolvo plo Prof. Dr. Emlon Rocha Olvra, EEE-UFG, 6. Propra a ranformaa Laplac Propra a convolção. propra a convolção no omíno o mpo m ma vaa aplcação na anál o ma lnar. Dao o na () h(), cja
nál Sma Lnar Dnvolvo plo Prof. Dr. Emlon Rocha Olvra, EEE-UFG, 6. Propra a ranformaa Laplac Propra a convolção. propra a convolção no omíno o mpo m ma vaa aplcação na anál o ma lnar. Dao o na () h(), cja
UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DEPARTAMENTO DE ECONOMIA
 UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DEPARTAMENTO DE ECONOMIA EAE 26 Macroconoma I º Smstr 27 Príoo Durno Profssors: lbrto Tau Lma Pro arca Duart Lsta Exrcícos
UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DEPARTAMENTO DE ECONOMIA EAE 26 Macroconoma I º Smstr 27 Príoo Durno Profssors: lbrto Tau Lma Pro arca Duart Lsta Exrcícos
Variáveis aleatórias Conceito de variável aleatória
 Variávis alatórias Muitos primtos alatórios produzm rsultados ão-uméricos. Ats d aalisá-los, é covit trasformar sus rsultados m úmros, o qu é fito através da variávl alatória, qu é uma rgra d associação
Variávis alatórias Muitos primtos alatórios produzm rsultados ão-uméricos. Ats d aalisá-los, é covit trasformar sus rsultados m úmros, o qu é fito através da variávl alatória, qu é uma rgra d associação
Definição clássica de probabilidade. Seja S finito e S, o número de elementos de S, por exemplo, quaisquer!,! 0 2 S. Então
 Dfiição clássica probabili Dfiição Sja S fiito S o úmro lmtos S por xmplo S {a b c S 3 Supoha P({) P({ 0 )para quaisr 0 2 S Etão P({) /S Dmostração Como S é do tipo S { 2 o S sgu S { [ { 2 [ [ { portato
Dfiição clássica probabili Dfiição Sja S fiito S o úmro lmtos S por xmplo S {a b c S 3 Supoha P({) P({ 0 )para quaisr 0 2 S Etão P({) /S Dmostração Como S é do tipo S { 2 o S sgu S { [ { 2 [ [ { portato
NÚMEROS COMPLEXOS. Podemos definir o conjunto dos números complexos como sendo o conjunto dos números escritos na forma:
 NÚMEROS COMPLEXOS DEFINIÇÃO No cojuto dos úmros ras R, tmos qu a a a é smpr um úmro ão gatvo para todo a Ou sja, ão é possívl xtrar a ra quadrada d um úmro gatvo m R Portato, podmos dfr um cojuto d úmros
NÚMEROS COMPLEXOS DEFINIÇÃO No cojuto dos úmros ras R, tmos qu a a a é smpr um úmro ão gatvo para todo a Ou sja, ão é possívl xtrar a ra quadrada d um úmro gatvo m R Portato, podmos dfr um cojuto d úmros
COLÉGIO OBJETIVO JÚNIOR
 COLÉGIO OBJETIVO JÚNIOR NOME: N. o : 7. o ANO DATA: / /201 FOLHETO DE MATEMÁTICA (V.C. E R.V.) Este fo lhe to é um ro te i ro de es tu do para você re cu pe rar o con te ú do tra ba lha do em 201. Como
COLÉGIO OBJETIVO JÚNIOR NOME: N. o : 7. o ANO DATA: / /201 FOLHETO DE MATEMÁTICA (V.C. E R.V.) Este fo lhe to é um ro te i ro de es tu do para você re cu pe rar o con te ú do tra ba lha do em 201. Como
3. VARIÁVEIS ALEATÓRIAS
 3. VARIÁVEIS ALEATÓRIAS 0 Varávl alatóra Ω é o spaço amostral d um prmnto alatóro. Uma varávl alatóra,, é uma função qu atrbu um númro ral a cada rsultado m Ω. Emplo. Rtra-s, ao acaso, um tm produzdo d
3. VARIÁVEIS ALEATÓRIAS 0 Varávl alatóra Ω é o spaço amostral d um prmnto alatóro. Uma varávl alatóra,, é uma função qu atrbu um númro ral a cada rsultado m Ω. Emplo. Rtra-s, ao acaso, um tm produzdo d
Disciplina: Análise Multivariada I Prof. Dr. Admir Antonio Betarelli Junior AULA 6.1
 Dscpla: álse Multvaraa I Prof. Dr. mr too Betarell Juor UL 6. MÉTODO DE ESCLONMENTO MULTIDIMENSIONL (MDS) Proposto por Youg (987) esse métoo poe ser utlzao para agrupameto. É uma técca para represetar
Dscpla: álse Multvaraa I Prof. Dr. mr too Betarell Juor UL 6. MÉTODO DE ESCLONMENTO MULTIDIMENSIONL (MDS) Proposto por Youg (987) esse métoo poe ser utlzao para agrupameto. É uma técca para represetar
rs r r ã tr ê s 1 t s rt t t át Pr r Pós r çã t át çõ s ét çã t át à tr ã ís
 rs r r ã tr ê s 1 t s rt t t át Pr r Pós r çã t át çõ s ét çã t át à tr ã ís çõ s ét çã t át à tr ss rt çã r s t Pr r Pós r çã t át r q s t r r t çã r str t át r t r Pr t r s r r t r t át ã ís Ficha gerada
rs r r ã tr ê s 1 t s rt t t át Pr r Pós r çã t át çõ s ét çã t át à tr ã ís çõ s ét çã t át à tr ss rt çã r s t Pr r Pós r çã t át r q s t r r t çã r str t át r t r Pr t r s r r t r t át ã ís Ficha gerada
NOTA: ESCREVA AS RESPOSTAS COMO FRAÇÕES OU COM 4 CASAS DECIMAIS NOTA 2: O FORMULÁRIO ESTÁ NO FINAL DA PROVA
 IND 5 Ifrêca statístca Smstr 7. Tst 3//7 Nom: NOTA: SCRVA AS RSPOSTAS COMO FRAÇÕS OU COM 4 CASAS DCIMAIS NOTA : O FORMULÁRIO STÁ NO FINAL DA PROVA Problma (5 potos A quatdad d rfrgrat uma garrafa PT d
IND 5 Ifrêca statístca Smstr 7. Tst 3//7 Nom: NOTA: SCRVA AS RSPOSTAS COMO FRAÇÕS OU COM 4 CASAS DCIMAIS NOTA : O FORMULÁRIO STÁ NO FINAL DA PROVA Problma (5 potos A quatdad d rfrgrat uma garrafa PT d
sendo classificado como modelo de primeira ordem com (p) variáveis independentes.
 RGRSSAO MULTIPLA - comlmtação Itrodução O modlo lar d rgrssão múltla é da forma: sdo classfcado como modlo d rmra ordm com () varávs ddts. od: é a varávl d studo (ddt, xlcada, rsosta ou dóga); é o cofct
RGRSSAO MULTIPLA - comlmtação Itrodução O modlo lar d rgrssão múltla é da forma: sdo classfcado como modlo d rmra ordm com () varávs ddts. od: é a varávl d studo (ddt, xlcada, rsosta ou dóga); é o cofct
MODELOS DE REGRESSÃO NÃO LINEARES
 M. Mede de Olvera Excerto da ota peoa obre: MODELOS DE REGRESSÃO NÃO LINEARES Obervação No modelo de regreão dto leare, a varável depedete é exprea como fução lear do coefcete de regreão. É rrelevate,
M. Mede de Olvera Excerto da ota peoa obre: MODELOS DE REGRESSÃO NÃO LINEARES Obervação No modelo de regreão dto leare, a varável depedete é exprea como fução lear do coefcete de regreão. É rrelevate,
Indice de Gini. Como existem N (N 1 ) / 2 pares distintos, o Gini corresponde a :
 Idc d G Itrprtação Gométrca. Corrspod à razão tr a ára tr a curva a rta d prfta gualdad a ára total sob a rta d prfta gualdad (vara d 0 a. Emplo d Fução Bm Estar Socal Basada o G: A fução Bm Estar Socal
Idc d G Itrprtação Gométrca. Corrspod à razão tr a ára tr a curva a rta d prfta gualdad a ára total sob a rta d prfta gualdad (vara d 0 a. Emplo d Fução Bm Estar Socal Basada o G: A fução Bm Estar Socal
C5 C O termo geral do desenvolvimento de A( x ) é. Assim, vem: Número de casos possíveis: 6 C
 Tst d avalação Pág Estm duas stuaçõs, a sabr: A Crsta ão va, ortato, o Atóo também ão va Os quatro blhts srão dstrbuídos los rstats quatro jovs, assm, o úmro d gruos é gual a um A Crsta va; os rstats três
Tst d avalação Pág Estm duas stuaçõs, a sabr: A Crsta ão va, ortato, o Atóo também ão va Os quatro blhts srão dstrbuídos los rstats quatro jovs, assm, o úmro d gruos é gual a um A Crsta va; os rstats três
Física Computacional 5
 Física Computacioal 5. Drivaas com irças iitas a. O cocito rivaa mos simpls qu o itgral b. Cálculo umérico a rivaa com irças iitas c. Um outro cocito Equação Dircial Oriária. Solução aalítica as EDO liars.
Física Computacioal 5. Drivaas com irças iitas a. O cocito rivaa mos simpls qu o itgral b. Cálculo umérico a rivaa com irças iitas c. Um outro cocito Equação Dircial Oriária. Solução aalítica as EDO liars.
MA12 - Unidade 4 Somatórios e Binômio de Newton Semana de 11/04 a 17/04
 MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
Estatística Estimação de Parâmetros por Intervalo
 Etatítica - Etimação d Parâmtro por Itrvalo UNESP FEG DPD Prof. Edgard - - Itrvalo d Cofiaça para a média População ifiita, com cohcido Sab- qu, para uficitmt grad: Normal ( ; /) Sja: : Erro ou Prcião
Etatítica - Etimação d Parâmtro por Itrvalo UNESP FEG DPD Prof. Edgard - - Itrvalo d Cofiaça para a média População ifiita, com cohcido Sab- qu, para uficitmt grad: Normal ( ; /) Sja: : Erro ou Prcião
1. A TRANSFORMADA DE LAPLACE
 Equaçõ Difrciai - Traformada d Laplac A TRANSFORMADA DE LAPLACE Dfiição: Sja f() uma fução ral dfiida para > Eão a raformada d Laplac d f(), doada por L [ ( ) ] f é dfiida por: L [ f ( ) ] F( ) f( )d,
Equaçõ Difrciai - Traformada d Laplac A TRANSFORMADA DE LAPLACE Dfiição: Sja f() uma fução ral dfiida para > Eão a raformada d Laplac d f(), doada por L [ ( ) ] f é dfiida por: L [ f ( ) ] F( ) f( )d,
Resolução de Matemática da Prova Objetiva FGV Administração - 06-06-10
 QUESTÃO 1 VESTIBULAR FGV 010 JUNHO/010 RESOLUÇÃO DAS 15 QUESTÕES DE MATEMÁTICA DA PROVA DA MANHÃ MÓDULO OBJETIVO PROVA TIPO A O mon i tor de um note book tem formato retangular com a di ag o nal medindo
QUESTÃO 1 VESTIBULAR FGV 010 JUNHO/010 RESOLUÇÃO DAS 15 QUESTÕES DE MATEMÁTICA DA PROVA DA MANHÃ MÓDULO OBJETIVO PROVA TIPO A O mon i tor de um note book tem formato retangular com a di ag o nal medindo
Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e :
 INSCRIÇÕES ABERTAS ATÉ 13 DE JULH DE 2015! Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e : Caso vo cê nunca t e nh a pa
INSCRIÇÕES ABERTAS ATÉ 13 DE JULH DE 2015! Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e : Caso vo cê nunca t e nh a pa
sen( x h) sen( x) sen xcos h sen hcos x sen x
 MAT00 Cálculo Difrcial Itgral I RESUMO DA AULA TEÓRICA Livro do Stwart: Sçõs 3., 3.4 3.8. DEMONSTRAÇÕES Nssa aula srão aprstadas dmostraçõs, ou sboços d dmostraçõs, d algus rsultados importats do cálculo
MAT00 Cálculo Difrcial Itgral I RESUMO DA AULA TEÓRICA Livro do Stwart: Sçõs 3., 3.4 3.8. DEMONSTRAÇÕES Nssa aula srão aprstadas dmostraçõs, ou sboços d dmostraçõs, d algus rsultados importats do cálculo
TRANSFORMADAS DE FOURIER
 TRASORMADAS DE OURIER Dfção: É a raformação qu lva uma magm a r rprada o domío da frqüêca Io é poívl porqu uma magm pod r dcompoa m fuçõ o coo com dfr frqüêca amplud A vaagm prcpal d rabalhar o domío da
TRASORMADAS DE OURIER Dfção: É a raformação qu lva uma magm a r rprada o domío da frqüêca Io é poívl porqu uma magm pod r dcompoa m fuçõ o coo com dfr frqüêca amplud A vaagm prcpal d rabalhar o domío da
XXXI Olimpíada Brasileira de Matemática GABARITO Primeira Fase
 XXXI Olimpíada Brasilira d Matmática GABARITO Primira Fas Soluçõs Nívl Uivrsitário Primira Fas PROBLEMA ( x) a) A drivada da fução f é f ( x) =, qu s aula apas para x =, sdo gativa para x < positiva para
XXXI Olimpíada Brasilira d Matmática GABARITO Primira Fas Soluçõs Nívl Uivrsitário Primira Fas PROBLEMA ( x) a) A drivada da fução f é f ( x) =, qu s aula apas para x =, sdo gativa para x < positiva para
Não serão feitos esclarecimentos individuais sobre questões durante a prova. Não se esqueça que tudo é para justificar.
 Eam m 7 d Jairo d 007 Cálculo ATENÇÃO: FOLHAS DE EXAE NÃO IDENTIFICADAS NÃO SERÃO COTADAS Cálculo / Eam fial ª Época 7 Jairo d 007 Duração: horas 0 miutos Rsolva os grupos do am m folhas sparadas O uso
Eam m 7 d Jairo d 007 Cálculo ATENÇÃO: FOLHAS DE EXAE NÃO IDENTIFICADAS NÃO SERÃO COTADAS Cálculo / Eam fial ª Época 7 Jairo d 007 Duração: horas 0 miutos Rsolva os grupos do am m folhas sparadas O uso
Capítulo 1: Erros em cálculo numérico
 Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Índice alfabético. página: 565 a b c d e f g h i j k l m n o p q r s t u v w x y z. procura índice imprimir última página vista anterior seguinte
 Í é á: 565 á é í ú á í é á: 566 A A é, 376 A, 378 379 A á, 146 147 A, 309 310 A á, 305 A ( ), 311 A, 305 308 A á B, 470 A á, 384 385 A,, ç Bç, 338 340 A é, 337 Aé, 333 A, 410 419 A K, 466 A, 123 A, 32
Í é á: 565 á é í ú á í é á: 566 A A é, 376 A, 378 379 A á, 146 147 A, 309 310 A á, 305 A ( ), 311 A, 305 308 A á B, 470 A á, 384 385 A,, ç Bç, 338 340 A é, 337 Aé, 333 A, 410 419 A K, 466 A, 123 A, 32
1. Revisão Matemática
 1. Revsão Matemátca Dervadas Seja a fução f : R R, fxe x R, e cosdere a expressão : f ( x+ αe ) lmα 0 α f, ode e é o vector utáro. Se o lmte acma exstr, chama-se a dervada parcal de f o poto x e é represetado
1. Revsão Matemátca Dervadas Seja a fução f : R R, fxe x R, e cosdere a expressão : f ( x+ αe ) lmα 0 α f, ode e é o vector utáro. Se o lmte acma exstr, chama-se a dervada parcal de f o poto x e é represetado
RESULTADOS DA PESQUISA DE SATISFAÇÃO DO USUÁRIO EXTERNO COM A CONCILIAÇÃO E A MEDIAÇÃO
 RESULTADOS DA PESQUISA DE SATISFAÇÃO DO USUÁRIO EXTERNO COM A CONCILIAÇÃO E A MEDIAÇÃO 1. RESULTADOS QUESTIONÁRIO I - PARTES/ CONCILIAÇÃO 1.1- QUESTIONÁRIO I - PARTES/ CONCILIAÇÃO: AMOSTRA REFERENTE AS
RESULTADOS DA PESQUISA DE SATISFAÇÃO DO USUÁRIO EXTERNO COM A CONCILIAÇÃO E A MEDIAÇÃO 1. RESULTADOS QUESTIONÁRIO I - PARTES/ CONCILIAÇÃO 1.1- QUESTIONÁRIO I - PARTES/ CONCILIAÇÃO: AMOSTRA REFERENTE AS
NOTAS DE AULA DA DISCIPLINA CE076
 9. ANÁISE DE AGUPAENTOS (CUSTER) 9. INTRODUÇÃO A Aálse e Agruametos é uma técca stta os étoos e Classfcação (Aálse Dscrmate, Regressão ogístca). Na Classfcação temos um úmero e gruos cohecos, e o objetvo
9. ANÁISE DE AGUPAENTOS (CUSTER) 9. INTRODUÇÃO A Aálse e Agruametos é uma técca stta os étoos e Classfcação (Aálse Dscrmate, Regressão ogístca). Na Classfcação temos um úmero e gruos cohecos, e o objetvo
1 1 2π. Área de uma Superfície de Revolução. Área de uma Superfície de Revolução
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Ára d uma Suprfíc
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Ára d uma Suprfíc
Estratégico. III Seminário de Planejamento. Rio de Janeiro, 23 a 25 de fevereiro de 2011
 Estratégico III Seminário de Planejamento Rio de Janeiro, 23 a 25 de fevereiro de 2011 G es tão Em pre sa rial O rie nta ção pa ra om erc ado Ino vaç ão et
Estratégico III Seminário de Planejamento Rio de Janeiro, 23 a 25 de fevereiro de 2011 G es tão Em pre sa rial O rie nta ção pa ra om erc ado Ino vaç ão et
INFLUÊNCIA DOS FENÔMENOS EL NIÑO E LA NIÑA NA FREQÜENCIA E DISTRIBUIÇÃO DE GEADAS NA REGIÃO DE PELOTAS - RS. RESUMO
 INLUÊNCIA DOS ENÔMENOS EL NIÑO E LA NIÑA NA REQÜENCIA E DISTRIBUIÇÃO DE EADAS NA REIÃO DE PELOTAS - RS. Rogo RIZZI, o Nto ASSIS, Mt El ozlz MENDEZ, Cláu Rj Joo CAMPOS, Joé Clo LAO RESUMO Avlou- o fto o
INLUÊNCIA DOS ENÔMENOS EL NIÑO E LA NIÑA NA REQÜENCIA E DISTRIBUIÇÃO DE EADAS NA REIÃO DE PELOTAS - RS. Rogo RIZZI, o Nto ASSIS, Mt El ozlz MENDEZ, Cláu Rj Joo CAMPOS, Joé Clo LAO RESUMO Avlou- o fto o
GLOSSÁRIO PREV PEPSICO
 GLOSSÁRIO PREV PEPSICO A T A A ABRAPP Aã Aã I Aí I R ANAPAR A A M A A A Lí Aá S C é ç í ê çõ 13ª í ã. Açã B E F Pê P. Cí ê, ã ê. V Cê Aã P ( á). N í, - I R P Fí (IRPF), S R F, à í á, ( 11.053 2004), çã.
GLOSSÁRIO PREV PEPSICO A T A A ABRAPP Aã Aã I Aí I R ANAPAR A A M A A A Lí Aá S C é ç í ê çõ 13ª í ã. Açã B E F Pê P. Cí ê, ã ê. V Cê Aã P ( á). N í, - I R P Fí (IRPF), S R F, à í á, ( 11.053 2004), çã.
Em termos da fração da renda total da população recebida por cada pessoa, na distribuição dual temos. pessoas
 6. Dual do Ídic d hil Dfiição Gral do Dual: Sja x uma variávl alatória com média µ distribuição tal qu o valor d crta mdida d dsigualdad é M. Chama-s dual a distribuição com as sguits caractrísticas: a.
6. Dual do Ídic d hil Dfiição Gral do Dual: Sja x uma variávl alatória com média µ distribuição tal qu o valor d crta mdida d dsigualdad é M. Chama-s dual a distribuição com as sguits caractrísticas: a.
Trem Bala Ana Vilela Arr. Danilo Andrade/Regina Damiati
 core Trem ala na Vilela rr. Danilo ndrade/regina Damiati oprano c D G D G Œ Œ r lto c Não é so bre Œ Œ r aritone c Não é so bre 5. ter to - das as pes - so - as do mun - do pra si é so-bre sa -. ter to
core Trem ala na Vilela rr. Danilo ndrade/regina Damiati oprano c D G D G Œ Œ r lto c Não é so bre Œ Œ r aritone c Não é so bre 5. ter to - das as pes - so - as do mun - do pra si é so-bre sa -. ter to
/11/00 2:12 AM
 Aguas de março Waters of March Antonio arlos Jobim arr. laus Ogerman Moderato É 1 F b.. b b.. b.. rhythm 5 pau, é pedra, é_o fim do ca - minho. b. rhythm É_um res - to de toco, n b é um pou - co so -zinho
Aguas de março Waters of March Antonio arlos Jobim arr. laus Ogerman Moderato É 1 F b.. b b.. b.. rhythm 5 pau, é pedra, é_o fim do ca - minho. b. rhythm É_um res - to de toco, n b é um pou - co so -zinho
Módulo 03. Determinantes. [Poole 262 a 282]
![Módulo 03. Determinantes. [Poole 262 a 282] Módulo 03. Determinantes. [Poole 262 a 282]](/thumbs/74/70829060.jpg) Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost
Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost
Código PE-ACSH-2. Título:
 CISI Ctro Itrção Srvços Iformtc rão Excução Atv Itr o CISI Cóo Emto por: Grêc o Stor 1. Objtvo cmpo plcção Est ocumto tm como fl fr o prão brtur chmos suport o CISI. A brtur chmos é rlz o sstm hlpsk, qu
CISI Ctro Itrção Srvços Iformtc rão Excução Atv Itr o CISI Cóo Emto por: Grêc o Stor 1. Objtvo cmpo plcção Est ocumto tm como fl fr o prão brtur chmos suport o CISI. A brtur chmos é rlz o sstm hlpsk, qu
Organização e Arquitetura de computadores
 gaização Aquiua compuao oução Pipliigéuma écica implmação m qu váia iuçõ ão obpoa a xcução Exmplo: lavagm oupa Mlhoao o mpho com pipliig Pof. D. Luciao Joé Sg Pipliig abalho é iviio m apa ou ágio Técica
gaização Aquiua compuao oução Pipliigéuma écica implmação m qu váia iuçõ ão obpoa a xcução Exmplo: lavagm oupa Mlhoao o mpho com pipliig Pof. D. Luciao Joé Sg Pipliig abalho é iviio m apa ou ágio Técica
Critérios de Avaliação do Ensino Básico - 3º Ciclo
 Crtéro d Avalação do Enno Báo - 3º Clo Língua Portugua ATITUDES Formação para a dadana. DOMÍNIOS DO CONHECIMENTO E PERCENTAGENS COMPETÊNCIAS Comprnão oral ACTIVIDADES/ /INSTRUMENTOS DE AVALIAÇÃO Ralzação
Crtéro d Avalação do Enno Báo - 3º Clo Língua Portugua ATITUDES Formação para a dadana. DOMÍNIOS DO CONHECIMENTO E PERCENTAGENS COMPETÊNCIAS Comprnão oral ACTIVIDADES/ /INSTRUMENTOS DE AVALIAÇÃO Ralzação
CONTROLADOR ADAPTATIVO POR MODELO DE REFERÊNCIA E ESTRUTURA VARIÁVEL APLICADO AO CONTROLE DE UM GERADOR SÍNCRONO
 OROLAOR AAAIVO OR MOELO E REFERÊIA E ESRUURA VARIÁVEL ALIAO AO OROLE E UM GERAOR SÍROO MARUS V A FERAES ARE LIMA E ALAYR ARAÚJO Lboóo Acoo ool Ição o Eh Eléc Uv Fl o Ro G o o 9-9 - l R Bl E-l: cv@lco @yhooco
OROLAOR AAAIVO OR MOELO E REFERÊIA E ESRUURA VARIÁVEL ALIAO AO OROLE E UM GERAOR SÍROO MARUS V A FERAES ARE LIMA E ALAYR ARAÚJO Lboóo Acoo ool Ição o Eh Eléc Uv Fl o Ro G o o 9-9 - l R Bl E-l: cv@lco @yhooco
Matemática. Resolução das atividades complementares. M18 Noções de Estatística
 Resolução das atvdades complemetares Matemátca M8 Noções de Estatístca p. 3 (UFRJ) Dos estados do país, um certo ao, produzem os mesmos tpos de grãos. Os grácos de setores lustram a relação etre a produção
Resolução das atvdades complemetares Matemátca M8 Noções de Estatístca p. 3 (UFRJ) Dos estados do país, um certo ao, produzem os mesmos tpos de grãos. Os grácos de setores lustram a relação etre a produção
EXPERIÊNCIA 7 MEDIDA DE INDUTÂNCIA POR ONDA RETANGULAR
 UMCCE Eng. Elérca m - ab. Crco Elérco Prof. Wlon Yamag EXPEÊNC 7 MEDD DE NDUÂNC PO OND ENGU NODUÇÃO O objvo báco da xprênca é mdr a ndânca a rênca d ma bobna zando ma onda ranglar. O prncípo da mdção é
UMCCE Eng. Elérca m - ab. Crco Elérco Prof. Wlon Yamag EXPEÊNC 7 MEDD DE NDUÂNC PO OND ENGU NODUÇÃO O objvo báco da xprênca é mdr a ndânca a rênca d ma bobna zando ma onda ranglar. O prncípo da mdção é
Ainda há Tempo, Volta
 Ainda há empo, Volta Letra e Música: Diogo Marques oprano ontralto Intro Envolvente (q = 60) enor aixo Piano Ó Œ. R.. F m7 2 A b 2 E b.. 2 Ó Œ É 2 Ó Œ F m7 2.. 2 2 A b 2 2 Ainda há empo, Volta Estrofe
Ainda há empo, Volta Letra e Música: Diogo Marques oprano ontralto Intro Envolvente (q = 60) enor aixo Piano Ó Œ. R.. F m7 2 A b 2 E b.. 2 Ó Œ É 2 Ó Œ F m7 2.. 2 2 A b 2 2 Ainda há empo, Volta Estrofe
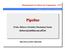 http://www.ic.uff.b/~boa/fac! 1 Ana, Buno, Cala, Luiz tê oupa uja a lavaa, caa, obaa guaaa Lavaoa lva 30 inuto Scaoa lva 30 inuto Doba lva 30 inuto Guaa lva 30 inuto A B C D 2 6 PM 7 8 9 10 11 12 1 2 AM
http://www.ic.uff.b/~boa/fac! 1 Ana, Buno, Cala, Luiz tê oupa uja a lavaa, caa, obaa guaaa Lavaoa lva 30 inuto Scaoa lva 30 inuto Doba lva 30 inuto Guaa lva 30 inuto A B C D 2 6 PM 7 8 9 10 11 12 1 2 AM
MONITORAMENTO DE INFORMAÇÃO
 Consórcio muda d ndrço Corrio Lagano - 20/01/2016 5 - Colunista - Olivt Salmória Mídia Imprssa Co m d n 1 Içara prd vantagm comptitiva 9/01) Diário d Notícias/Criciúma - 20/01/2016 7 - Gral Mídia Imprssa
Consórcio muda d ndrço Corrio Lagano - 20/01/2016 5 - Colunista - Olivt Salmória Mídia Imprssa Co m d n 1 Içara prd vantagm comptitiva 9/01) Diário d Notícias/Criciúma - 20/01/2016 7 - Gral Mídia Imprssa
Espaço de Estados. Modelo de Estado: y(t) = saída u(t) = entrada. função de transferência em cadeia fechada (f.t.c.f) :
 Epço Eo Eqo or corolo covcol - rlção r í-r, o fção rfrêc, o corolo moro - crção qçõ o m m rmo qçõ frc ªorm q pom r com m qção frcl ª orm form mrcl. O o oção mrcl mplfc m mo rprção mmác m qçõ. O mo úmro
Epço Eo Eqo or corolo covcol - rlção r í-r, o fção rfrêc, o corolo moro - crção qçõ o m m rmo qçõ frc ªorm q pom r com m qção frcl ª orm form mrcl. O o oção mrcl mplfc m mo rprção mmác m qçõ. O mo úmro
( C) lim g( x) 2x 4 0 ( D) lim g( x) 2x
 AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha d Trabalho º6 - Fuçõs - º ao Eams 0 a 04. Na figura stá rprstada um rfrcial o.. Oy, part do gráfico d uma fução g, d domíio 3,. A rta d quação y 4 é assítota do
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha d Trabalho º6 - Fuçõs - º ao Eams 0 a 04. Na figura stá rprstada um rfrcial o.. Oy, part do gráfico d uma fução g, d domíio 3,. A rta d quação y 4 é assítota do
Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I. Ano Lectivo º Semestre
 Faculdad d Ecoomia Uivrsidad Nova d Lisboa EXAME DE CÁLCULO I Ao Lctivo 8-9 - º Smstr Eam Fial d ª Época m d Jairo 9 Tópicos d Corrcção Duração: horas miutos É proibido usar máquias d calcular ou tlmóvis
Faculdad d Ecoomia Uivrsidad Nova d Lisboa EXAME DE CÁLCULO I Ao Lctivo 8-9 - º Smstr Eam Fial d ª Época m d Jairo 9 Tópicos d Corrcção Duração: horas miutos É proibido usar máquias d calcular ou tlmóvis
Resolução feita pelo Intergraus! Módulo Objetivo - Matemática FGV 2010/1-13.12.2009
 FGV 010/1-13.1.009 VESTIBULAR FGV 010 DEZEMBRO 009 MÓDULO OBJETIVO PROVA TIPO A PROVA DE MATEMÁTICA QUESTÃO 1 (Prova: Tipo B Resposta E; Tipo C Resposta C; Tipo D Resposta A) O gráfico abaio fornece o
FGV 010/1-13.1.009 VESTIBULAR FGV 010 DEZEMBRO 009 MÓDULO OBJETIVO PROVA TIPO A PROVA DE MATEMÁTICA QUESTÃO 1 (Prova: Tipo B Resposta E; Tipo C Resposta C; Tipo D Resposta A) O gráfico abaio fornece o
TEMA 3 NÚMEROS COMPLEXOS FICHAS DE TRABALHO 12.º ANO COMPILAÇÃO TEMA 3 NÚMEROS COMPLEXOS. Jorge Penalva José Carlos Pereira Vítor Pereira MathSuccess
 FICHAS DE TRABALHO º ANO COMPILAÇÃO TEMA NÚMEROS COMPLEXOS St: http://wwwmathsuccsspt Facbook: https://wwwfacbookcom/mathsuccss TEMA NÚMEROS COMPLEXOS Matmátca A º Ano Fchas d Trabalho Complação Tma Númros
FICHAS DE TRABALHO º ANO COMPILAÇÃO TEMA NÚMEROS COMPLEXOS St: http://wwwmathsuccsspt Facbook: https://wwwfacbookcom/mathsuccss TEMA NÚMEROS COMPLEXOS Matmátca A º Ano Fchas d Trabalho Complação Tma Númros
A solução mais geral da equação anterior tem a forma: α 2 2. Aplicando estes resultados na equação do MHS, temos que:
 . qação para o MHS Qano o oino corpo cr a rajória, a parir cro inan coça a rpir a rajória, izo q oino é prióico. O po q o corpo gaa para olar a prcorrr o o pono a rajória é chaao príoo. No noo coiiano
. qação para o MHS Qano o oino corpo cr a rajória, a parir cro inan coça a rpir a rajória, izo q oino é prióico. O po q o corpo gaa para olar a prcorrr o o pono a rajória é chaao príoo. No noo coiiano
 J u i n 2 0 0 9 L e ttr e d 'i n fo r m a ti o n n 1 9 E d i to r i al E p p u r si m u o ve «E t p o u r ta n t e l l e b o u g e» m u r m u r a G a l l i l é e s u r s o n c h a m p e s t l a r g e.
J u i n 2 0 0 9 L e ttr e d 'i n fo r m a ti o n n 1 9 E d i to r i al E p p u r si m u o ve «E t p o u r ta n t e l l e b o u g e» m u r m u r a G a l l i l é e s u r s o n c h a m p e s t l a r g e.
Pág Circunferência: ( ) ( ) 5.4. Circunferência: ( ) ( ) A reta r passa nos pontos de coordenadas (0, 1) e (2, 2).
 Númros complxos Atvdad d dagnóstco AB + + + AB ( ) ( ) ( ) + + + 9+ A, ; B, ; P x, y Pág AP BP x+ y x + y + x + x + + y x + x x + + y + x + yx y x A bsstr dos quadrants ímpars é a mdatr d [AB] B(, ) ;
Númros complxos Atvdad d dagnóstco AB + + + AB ( ) ( ) ( ) + + + 9+ A, ; B, ; P x, y Pág AP BP x+ y x + y + x + x + + y x + x x + + y + x + yx y x A bsstr dos quadrants ímpars é a mdatr d [AB] B(, ) ;
Identifique todas as folhas Folhas não identificadas NÃO SERÃO COTADAS. Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I
 Idtifiqu todas as folhas Folhas ão idtificadas NÃO SERÃO COTADAS Faculdad d Ecoomia Uivrsidad Nova d Lisboa EXAME DE CÁLCULO I Ao Lctivo 8-9 - º Smstr Exam Fial d ª Época m 5 d Maio 9 Duração: horas miutos
Idtifiqu todas as folhas Folhas ão idtificadas NÃO SERÃO COTADAS Faculdad d Ecoomia Uivrsidad Nova d Lisboa EXAME DE CÁLCULO I Ao Lctivo 8-9 - º Smstr Exam Fial d ª Época m 5 d Maio 9 Duração: horas miutos
1. O tempo que a partícula sai do ponto de deslocamento máximo e atinge o ponto de equilíbrio corresponde a. x m, o que nos conduz a:
 I INSIUO DE FÍSIC D UFB DEPRMENO DE FÍSIC GERL DISCIPLIN: FÍSIC GERL E EXPERIMENL II (FIS ) URM: 0 SEMESRE: /00 RESOLUÇÃO D a PROV D URM 0 O tp qu a partícula ai d pnt d dlcant áxi ating pnt d quilíbri
I INSIUO DE FÍSIC D UFB DEPRMENO DE FÍSIC GERL DISCIPLIN: FÍSIC GERL E EXPERIMENL II (FIS ) URM: 0 SEMESRE: /00 RESOLUÇÃO D a PROV D URM 0 O tp qu a partícula ai d pnt d dlcant áxi ating pnt d quilíbri
1 Eliminação gaussiana com pivotamento parcial
 1 Elimiação gaussiaa com pivotamto parcial Exmplo sm pivotamto parcial Costruimos a matriz complta: 0 2 2 1 1 1 6 0 2 2 1 2 1 1 1 1 0 2 2 1 1 1 6 1 2 0 0 2 0 6 x y z = 9 6 0 2 2 0 1 0 3 1 0 0 2 0 2 0 6
1 Elimiação gaussiaa com pivotamto parcial Exmplo sm pivotamto parcial Costruimos a matriz complta: 0 2 2 1 1 1 6 0 2 2 1 2 1 1 1 1 0 2 2 1 1 1 6 1 2 0 0 2 0 6 x y z = 9 6 0 2 2 0 1 0 3 1 0 0 2 0 2 0 6
Cálculo Diferencial e Integral II
 Cálculo Difrncial Intgral II Lista 7 - Rsumo a Toria A Rgra a Caia No stuo funçõs uma variávl usamos a Rgra a Caia para calcular a rivaa uma função composta Nst caso sno w f uma função ifrnciávl sno g
Cálculo Difrncial Intgral II Lista 7 - Rsumo a Toria A Rgra a Caia No stuo funçõs uma variávl usamos a Rgra a Caia para calcular a rivaa uma função composta Nst caso sno w f uma função ifrnciávl sno g
Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I. Ano Lectivo º Semestre
 aculdad d Ecoomia Uivrsidad Nova d Lisboa EXAME DE CÁLCULO I Ao Lctivo 009-0 - º Smstr Eam ial d ª Época m d Jairo d 00 Duração: horas 0 miutos É proibido usar máquias d calcular ou tlmóvis Não tha o su
aculdad d Ecoomia Uivrsidad Nova d Lisboa EXAME DE CÁLCULO I Ao Lctivo 009-0 - º Smstr Eam ial d ª Época m d Jairo d 00 Duração: horas 0 miutos É proibido usar máquias d calcular ou tlmóvis Não tha o su
N 5. JUVENTUDE em / in FORMAÇÃO. Pra você aprofundar no tema: REALIZAÇÃO: Livro: POESIA: MúSICA
 N 5 JUVENTUDE / FORMAÇÃO Lttu Mg Féz Cutu u t tóg L O qu é utu u At At P ê fu t: St bu: www.f..b www.utu.g.b www.fut.g.b www.ttuttt.g.b (k Cutu) www.bh.g.b (k Fuçõ; Fuçã Mu Cutu) www.utu.g.g.b www.u..b
N 5 JUVENTUDE / FORMAÇÃO Lttu Mg Féz Cutu u t tóg L O qu é utu u At At P ê fu t: St bu: www.f..b www.utu.g.b www.fut.g.b www.ttuttt.g.b (k Cutu) www.bh.g.b (k Fuçõ; Fuçã Mu Cutu) www.utu.g.g.b www.u..b
 REGULAMENTO DE INSTALAÇÃO E FUNCIONAMENTO DOS ESTABELECIMENTOS DE HOSPEDAGEM No u s o d a c o mp e t ê n c i a p r e v i s t a al í n e a v ) d o n. º 1 d o ar t i g o 64º d o De c r e t o -Le i n. º 1
REGULAMENTO DE INSTALAÇÃO E FUNCIONAMENTO DOS ESTABELECIMENTOS DE HOSPEDAGEM No u s o d a c o mp e t ê n c i a p r e v i s t a al í n e a v ) d o n. º 1 d o ar t i g o 64º d o De c r e t o -Le i n. º 1
TRANSFORMADA DE LAPLACE- PARTE I
 TRNSFORMD DE LLE- RTE I Eor. d Barro. INTRODUÇÃO odmo dfiir a Traformada d Laplac como uma opração mamáica qu covr uma fução d variávl ral m uma fução d variávl complxa: Od, F f d i f é uma fução ral da
TRNSFORMD DE LLE- RTE I Eor. d Barro. INTRODUÇÃO odmo dfiir a Traformada d Laplac como uma opração mamáica qu covr uma fução d variávl ral m uma fução d variávl complxa: Od, F f d i f é uma fução ral da
Trabalho 3. Gustavo Mello Reis Página 1
 Trabalho 3 Gustavo Mllo Ris Págia 1 1. Histograma a) Uma mprsa qu fabrica doc d lit dsja studar a distribuição da quatidad d doc lit por lata (), com o objtivo d visualizar a variação dsta. Para isto foi
Trabalho 3 Gustavo Mllo Ris Págia 1 1. Histograma a) Uma mprsa qu fabrica doc d lit dsja studar a distribuição da quatidad d doc lit por lata (), com o objtivo d visualizar a variação dsta. Para isto foi
Raciocínio-Lógico (Receita Federal 2009 Prova 1 - Gabarito 1):
 Racocío-Lógco (Rcta Fdral 009 Prova 1 - Gabarto 1): 1 Cosdr a sgut proposção: S chov ou va, tão o chão fca molhado. Sdo assm, pod-s afrmar qu: a) S o chão stá molhado, tão chovu ou vou b) S o chão stá
Racocío-Lógco (Rcta Fdral 009 Prova 1 - Gabarto 1): 1 Cosdr a sgut proposção: S chov ou va, tão o chão fca molhado. Sdo assm, pod-s afrmar qu: a) S o chão stá molhado, tão chovu ou vou b) S o chão stá
CADERNO 1 (É permitido o uso de calculadora gráfica.)
 Proposta de teste de avalação [mao 09] Nome: Ao / Turma: N.º: Data: - - Não é permtdo o uso de corretor. Deves rscar aqulo que pretedes que ão seja classfcado. A prova clu um formuláro. As cotações dos
Proposta de teste de avalação [mao 09] Nome: Ao / Turma: N.º: Data: - - Não é permtdo o uso de corretor. Deves rscar aqulo que pretedes que ão seja classfcado. A prova clu um formuláro. As cotações dos
6.15 EXERCÍCIOS pg. 290
 56 6.5 EXERCÍCOS pg. 9. Da um mplo d uma fução cotíua po pat dfiida o itvalo ] [. Muito mplo podm ciado. Sgu um dl: ) ( - - f - - - - - - 6 8 y. Calcula a itgal da guit fuçõ cotíua po pat dfiida o itvalo
56 6.5 EXERCÍCOS pg. 9. Da um mplo d uma fução cotíua po pat dfiida o itvalo ] [. Muito mplo podm ciado. Sgu um dl: ) ( - - f - - - - - - 6 8 y. Calcula a itgal da guit fuçõ cotíua po pat dfiida o itvalo
Estatística Clássica
 Estatística Clássica As rgias das difrts partículas do sistma (um istat particular s distribum d acordo com uma fução distribuição d probabilidad distribuição d Boltzma qu dpd da tmpratura T. Um xmplo
Estatística Clássica As rgias das difrts partículas do sistma (um istat particular s distribum d acordo com uma fução distribuição d probabilidad distribuição d Boltzma qu dpd da tmpratura T. Um xmplo
y z CC2: na saída do reator: z = 1: 0. Pe dz Os valores característicos do problema são as raízes de: Da Pe 0 Pe Pe
 COQ-86 Méodos Nuércos para Ssas Dsrbuídos Explos Ilusravos d EDO co Problas d Valors o Cooro -) Modlo sacoáro do raor co dsprsão soérco Coo o obvo ds sudo d caso é lusrar o ovo procdo avalar o su dspo
COQ-86 Méodos Nuércos para Ssas Dsrbuídos Explos Ilusravos d EDO co Problas d Valors o Cooro -) Modlo sacoáro do raor co dsprsão soérco Coo o obvo ds sudo d caso é lusrar o ovo procdo avalar o su dspo
Novo Espaço Matemática A 12.º ano Proposta de Teste [janeiro ]
![Novo Espaço Matemática A 12.º ano Proposta de Teste [janeiro ] Novo Espaço Matemática A 12.º ano Proposta de Teste [janeiro ]](/thumbs/80/81607224.jpg) Novo Espaço Matmática A.º ao Proposta d Tst [jairo - 08] Nom: Ao / Turma: N.º: Data: / / Não é prmitido o uso d corrtor. Dvs riscar aquilo qu prtds qu ão sja classificado. A prova iclui um formulário.
Novo Espaço Matmática A.º ao Proposta d Tst [jairo - 08] Nom: Ao / Turma: N.º: Data: / / Não é prmitido o uso d corrtor. Dvs riscar aquilo qu prtds qu ão sja classificado. A prova iclui um formulário.
1 i n o 3 Outubro de Em celebração aos 73 anos da Aperam, empregados compartilham suas histórias na Empresa
 LG A 1 3 O 2017 Pçã â T ê â ó. C? C ê z? A? A ê! á.6 R... é! E çã 73 A, ó E á.5 F: E N N Sá O ê á Fçã á.2 CCQ Cç 2017 Sá G Tó á.4 Á Cç, z á.8 L é V çã. U ç ã ê á ê í. - Mí S á.8 E I A 1 I P.2 I A 1 I P.3
LG A 1 3 O 2017 Pçã â T ê â ó. C? C ê z? A? A ê! á.6 R... é! E çã 73 A, ó E á.5 F: E N N Sá O ê á Fçã á.2 CCQ Cç 2017 Sá G Tó á.4 Á Cç, z á.8 L é V çã. U ç ã ê á ê í. - Mí S á.8 E I A 1 I P.2 I A 1 I P.3
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Exercícios de Cálculo Numérico - Erros
 Ercícios d Cálculo Numérico - Erros. Cosidr um computador d bits com pot máimo ( a rprstação m aritmética lutuat a bas. (a Dtrmi o mor úmro positivo rprstávl sta máquia a bas. (b Dtrmi o maior úmro positivo
Ercícios d Cálculo Numérico - Erros. Cosidr um computador d bits com pot máimo ( a rprstação m aritmética lutuat a bas. (a Dtrmi o mor úmro positivo rprstávl sta máquia a bas. (b Dtrmi o maior úmro positivo
Instituto Tecnológico de Aeronáutica. Prof. Carlos Henrique Q. Forster Sala 121 IEC. ramal 5981
 CCI-36 Computação Gráfca Modlo Radométrco Inttuto Tcnológco d Aronáutca Prof. Carlo Hnrqu Q. Fortr Sala 121 IEC ramal 5981 Tópco da aula BRDF Modlo d Phong Modlo d Gorraud Lvro para acompanhar a aula Horn
CCI-36 Computação Gráfca Modlo Radométrco Inttuto Tcnológco d Aronáutca Prof. Carlo Hnrqu Q. Fortr Sala 121 IEC ramal 5981 Tópco da aula BRDF Modlo d Phong Modlo d Gorraud Lvro para acompanhar a aula Horn
4 Regime Transitório de Turbinas a Gás 4.1. Introdução
 4 Rgim ranitório urbina a Gá 4.1. Introução O rgim tranitório a turbina a gá é caractrizao la conição muança o u rgim funcionamnto. O ríoo muança uma conição rgim rmannt ara outra conição rgim rmannt como,
4 Rgim ranitório urbina a Gá 4.1. Introução O rgim tranitório a turbina a gá é caractrizao la conição muança o u rgim funcionamnto. O ríoo muança uma conição rgim rmannt ara outra conição rgim rmannt como,
3. TRANSFORMADA DE LAPLACE. Prof. JOSÉ RODRIGO DE OLIVEIRA
 3 TRNSFORMD DE LPLCE Prof JOSÉ RODRIGO DE OLIVEIR CONCEITOS BÁSICOS Númro complxo: ond α β prncm ao nº rai Módulo fa d um númro complxo Torma d Eulr: b a an a co co n n Prof Joé Rodrigo CONCEITOS BÁSICOS
3 TRNSFORMD DE LPLCE Prof JOSÉ RODRIGO DE OLIVEIR CONCEITOS BÁSICOS Númro complxo: ond α β prncm ao nº rai Módulo fa d um númro complxo Torma d Eulr: b a an a co co n n Prof Joé Rodrigo CONCEITOS BÁSICOS
