Estrutura geral de um sistema com realimentação unitária negativa, com um compensador (G c (s) em série com a planta G p (s).
|
|
|
- Orlando de Sintra Gabeira
- 8 Há anos
- Visualizações:
Transcrição
1 2 CONTROLADORES PID Introdução Etrutura geral de um itema com realimentação unitária negativa, com um compenador (G c () em érie com a planta G p (). 2 Controladore PID 2. Acção proporcional (P) G c () = k, com k >. Principai caracterítica:. G c (jω)g p (jω) = k G p (jω) 2. (G c (jω)g p (jω)) = G p (jω) 3. localização de pólo em malha fechada obtida directamente do lugar geométrico da raíze 4. a frequência de traveia (ω π )de fae não depende de k (a) a margem de ganho varia inveramente com k MG = k G p(jω π) (b) aumento de k dimuinui margem de ganho 5. controlador proporcional não varia tipo de itema 6. contante de erro em regime permanente varia proporcionalmente com k 7. aumento de k melhora regime permanente Cao G p () tenha apena pólo no SPE ou na origem:. G p (jω) e G p (jω) diminuem com ω 2. aumento de k traduz-e num aumento da frequência de traveia de ganho (ω ) (a) diminuir margem de fae (b) aumenta largura de banda em malha fechada Cao G p () tenha um número de pólo uperior em mai de dua unidade ao número de zero ou tenha zero no SPD:. o itema realiamentado erá intável para valore de k elevado Exemplo 2.. Conideremo uma planta G p () = 6 (+2) 2. Um compenador proporcional G c () = k, permite diminuir o erro em regime permamente para entrada em degrau, que é decrecente com k e, degrau = + k/4 = k
2 2.2 Acção integral (I) 2 CONTROLADORES PID o pólo de malha fechada ão dado por + kg p () = k = endo (para k > ) = 2 ± j k A figura apreenta a repota ao degrau do itema realimentado, para valore de k, repectivamente de 6, 32 e 64. Neta figura é notória a diminuição do erro em regime permanente com o aumento de k, ma também o aumento da obreelongação, uma vez que o coeficiente de amortecimento diminui com o aumento de k, ζ = 2 k + 4. Para o valore de k indicado, o coeficiente de amortecimento ão repectivamente,.45,.33 e.24, correpondente a obreelongaçõe de 2%, 33% e 46% (e a frequência naturai não amortecida de 4.47, 6 e 8.25). Step Repone.4.2 Amplitude Time (ec) Figura : Repota ao degrau. 2.2 Acção integral (I) G c () = k I = T I Principai caracterítica:. G c () tem apena um pólo na origem 2. controlador integral aumenta em uma unidade o tipo de itema (a) e G p () for do tipo a acção integral elimina o erro em regime permanente para entrada em degrau (b) utilizado para melhorar o regime permanente 3. (G c (jω)g p (jω)) = 9 o + G p (jω) 4. G c (jω)g p (jω) G p (jω) para ω pequeno 5. G c (jω)g p (jω) G p (jω) para ω grande 2
3 2.2 Acção integral (I) 2 CONTROLADORES PID 6. a introdução do pólo na origem aumenta o número de aímptota do LGR (fazendo com que para k I elevado mai pólo paem para o SPD) 7. permite eliminar erro em regime permanente devido a perturbaçõe à entrada da planta, uma vez que G c ( ) Y () G p () = = = M() = + G c ()G p () = G c () = Comparação com controlo apena proporcional. habitualmente implica a dimunuição da frequência de traveia de fae 2. para manter uma margem de ganho emelhante normalmente requer uma diminuição da frequência de traveia de ganho, acarretando diminuição da largura de banda em malha fechada Exemplo 2.2. Conideremo novamente a planta G p () = (+2) e um compenador integral G 2 c () = k I /. O itema realimentado terá agora 3 pólo. Determinemo k I de modo que o pólo dominante tenham um coeficiente de amortecimento de.45 (igual ao obtido com um compenador proporcional G c () = 6). A equação caracterítica de malha fechada + G p ()G c () = toma agora a forma k I =. Coniderando que o itema realimentado tem um par de pólo complexo e um terceiro pólo (neceariamente real) localizado em a, a equação caracterítica correpondente erá ( + a)( 2 + 2ζω n + ω 2 n) = 3 + (a + 2ζω n ) 2 + (2aζω n + ω 2 n) + aω 2 n =. Da equivalência entre eta equaçõe reulta a + 2ζω n = 4 2aζω n + ωn 2 = 4 aωn 2 = k I Fazendo ζ =.5, como pretendido, e reolvendo o itema de equaçõe obtém-e ω n =.5, a = 3.6 e k I = A figura 2 apreenta a repota ao degrau do itema com ete compenador (e para comparação a repota com G c () = 6). Pode ver-e que o anulamento do erro ao degrau foi obtido à cuta de um diminuição da rapidez da repota, tal como eria de eperar (note-e a diminuição da frequência natural de 4.47 para.5). Step Repone.4.2 Amplitude Time (ec) Figura 2: Repota ao degrau. 3
4 2.3 Acção proporcional e integral (PI) 2 CONTROLADORES PID 2.3 Acção proporcional e integral (PI) G c () = k P + k I k P ganho proporcional k I ganho integral pode ainda ecrever-e G c () = k +z Principai caracterítica:. G c () tem um pólo na origem e um zero no SPE 2. não aumenta número de aímptota do LGR 3. G c (jω) = 9 o + arctan ω z (a) ω pequeno ( z) G c (jω) 9 o (G c (jω)g p (jω)) 9 o + G p (jω) (b) ω grande ( z) G c (jω) o (G c (jω)g p (jω)) G p (jω) Comparação com controlo apena proporcional ou apena integral. mantém caracterítica de melhoria de regime permanente e de eliminação de perturbaçõe da acção integral 2. G c (jω) aproxima-e de apena um ganho para ω z 3. fae poitiva devida ao zero no SPE permite aumentar frequência de traveia ou margen de etabilidade face à acção apena integral Projecto. doi grau de liberdade (k P, k I ou k, z) permitem atifazer doi critério ditinto 2. o projecto é por veze eparado em dua etapa (i) z é ecolhido de modo a cancelar um pólo de G p () (habitualmente o mai próximo da origem localizado no interior do SPE) (ii) k é ecolhido poteriormentede forma a cumprir algum requiito de regime tranitório (ζ ou ω n de pólo dominante em malha fechada), de margen de etabilidade,... Exemplo 2.3. Conideremo mai uma vez a planta G p () = (+2) 2 e agora um compenador PI G c () = k +z. Embora agora haja 2 parâmetro de ajute, vamo uar o zero do compenador para cancelar um pólo da plnata, ou eja, fazer z = 2 e determinar k de modo que o o pólo do itema em malha fechada (ápó o cancelamento ficam ó 2) tenham novamente um coeficiente de amortecimento de.45. A equação caracterítica de malha fechada + G p ()G c () =, toma agora a forma + k ( + 2) = k =. Teremo então 2ζω n = 2 e ωn 2 = k, pelo que endo ζ =.45 reulta ω n = 2.22 e k = O compenador PI erá então G c () = = A figura 3 apreenta a repota ao degrau do itema realimentado e, para comparação, também a repota ao degrau do itema realimentado com controlo integral apena, endo aí víivel o aumento de rapidez. 4
5 2.4 Acção derivativa (D) 2 CONTROLADORES PID Step Repone.4 PI I.2 Amplitude Time (ec) Figura 3: Repota ao degrau. 2.4 Acção derivativa (D) G c () = k D Principai caracterítica:. G c () tem apena um zero na origem 2. acção apena derivativa tem pouca (ou nenhuma) aplicação (a) poível cancelamento de pólo de G p () na origem (b) função de tranferência de malha fechada regime permanente para entrada em degrau! 3. G c (jω) = 9 o Gc()Gp() +G c ()G p () é nula para =, endo nula a repota em (a) habitualmente permite aumentar margen de etabilidade, em diminuir frequência de traveia 4. G c (jω) = k D ω (a) crece arbritariamente com ω, implicando amplificação crecente de inai de maior frequência, não endo aim imune a ruído de medida (b) ete efeito pode er compenado pela introdução de um pólo a uma frequência mai elevada, ou eja, G c () = k D +τ D 2.5 Acção proporcional e derivativa (PD) G c () = k P + k D = k( + z) Principai caracterítica:. zero no SPE em k P /k D (a) pode er uado para cancelar pólo mai lento de G p () (b) diminui o número de aímptota do LGR 2. G c (jω) = kp 2 + k2 D ω2 5
6 2.6 Acção proporcional, integral e derivativa (PID) 3 COMPENSAÇÃO EM ATRASO E EM AVANÇO (a) aumenta ilimitadamente quando ω +, com devantagen iguai à da acção apena derivativa (b) efeito pode er igualmente atenuado com introdução de um pólo a frequência mai elevada, ito é, G c () = k P +k D +τ D 3. G(jω) = arctan k Dω k P > Projecto (a) efeito benéfico na margen de etabilidade. doi grau de liberdade (k P, k D ) ou (k, z) permitem atifazer doi critério ditinto 2. zero pode er uado para cancelar pólo mai lento da planta 2.6 Acção proporcional, integral e derivativa (PID) G c () = k P + k I + k D = k I +k P +k D 2 = k(+z)(+z2) Principai caracterítica:. um pólo na origem 2. doi zero no SPD (podem er complexo) 3. G c (jω) + quando ω 4. G c (jω) 9 o quando ω 5. aumenta em uma unidade o tipo de itema, introduzindo melhoria no regime permanente 6. a fae introduzida a frequência apó o efeito do zero é poitiva, contribuindo para melhrar etabilidade ou rapidez (regime tranitório) 7. G c (jω) + quando ω + Projecto (a) amplificação de inai de alta frequência (b) pode er contrariado com introdução de um pólo a frequência maior que o zero. dipobibilidade de trê parâmetro permite ajutar imultaneamente trê grandeza 2. locvalização do zero pode er uada para cancelar pólo de G p () ou para alterar a configuração do LGR, endo então o ganho uado para ajute de pólo dominante ou margen etabilidade 3 Compenação em atrao e em avanço 3. Compenação atrao G c () = k +z +p, k, z, p >, p < z Principai caracterítica: 6
7 3. Compenação atrao 3 COMPENSAÇÃO EM ATRASO E EM AVANÇO. G c (jω) = arctan ω z arctan ω p < 2. G c () = kz/p 3. G c ( ) = k 4. G c (jω) dimuni com aumento de ω 5. a introdução de fae negativa habitualmente piora margen de etabilidade 6. habitualmente uado para melhorar regime permanente, tirando partido da caracterítica paa-baixo, evitando afectar regime tranitório e margen de etabilidade 7. fazer k = e z e p uficientemente abaixo de ω, ω π ou módulo do pólo dominante, de modo que a eta frequência e tenha G c (jω) Projecto (para melhorar regime permanente k = ):. ecolher z uma década abaixo de ω ou ω π ou módulo do pólo dominante 2. determinar p de modo que G c () = z/p permitar aumentar a contante de erro relevante tanto quanto pretendido Exemplo 3.. Conideremo a planta G p () = (+2) e pretende-e projectar um compenador atrao de modo 2 a aumentar 6 veze a contante de erro de poição. Admitindo inicialmente um compenador unitário, o pólo de malha fechada obtêm-e de = e localizam-e em 2 ± j, correpondendo a uma frequência natural não amortecida ω n = 2.24 e um coeficente de amortecimento de.89. Ecolhendo o zero do compenador uma década abaixo de ω n temo z =.224 e para aumentar 6 veze a contante de erro de poição deveremo ter z/p = 6, ficando p = z/6 =.373. O compenador ficará G c () = A figura 4 apreenta a repota ao degrau do itema realimentador, com e em compenador, endo facilmente viível vantagem em termo de regime permanente da compenação atrao. A figura 5 motra o traçado de Step Repone Amplitude não compenado compenado Time (ec) Figura 4: Repota ao degrau. bode de G p e de G c G p, onde e pode verificar que ete apena diferem na parte da baixa frequência. 7
8 3.2 Compenação avanço 3 COMPENSAÇÃO EM ATRASO E EM AVANÇO Bode Diagram 2 não compenado compenado Magnitude (db) Phae (deg) Frequency (rad/ec) Figura 5: Traçado de Bode. 3.2 Compenação avanço G c () = k +z +p, k, z, p >, z < p Principai caracterítica:. G c (jω) = arctan ω z arctan ω p > 2. G c (jω) aumenta com aumento de ω 3. G c (jω) é máximo para ω = ω max = zp 4. fae máxima do compenador é ϕ max = arcin α +α, onde α = z/p (a) α = in ϕ max +in ϕ max (b) z = ω max α (c) p = ω max / α 5. a introdução de fae poitiva habitualmente melhora margen de etabilidade 6. habitualmente uado para melhorar regime tranitório ou margen de etabilidade Projecto (para margen de etabilidade):. ecolher ω max igual à frequência de traveia de ganho ω 2. determinar ϕ max a partir da margem de fae deejada ϕ max + G p (jω max ) = 8 o + MF 3. determinar α = in ϕ max +in ϕ max 4. determinr k de modo que G c G p (jω max ) = Exemplo 3.2. Conideremo a planta G p () = (+2), para a qual e pretende projectar um compenador avanço de modo a que o itema realimentado tenha uma margem de fae de 45 a uma frequência de traveia de ganho ω =. A figura 6 apreenta o traçado de Bode de G p, onde e pode verificar que eta planta com realimentação unitária negativa apreenta uma margem de fae de 34.9 e uma frequência de traveia de ganho de Façamo então ω max = ω = e ϕ max = G p (j), ou eja, 8
9 3.2 Compenação avanço 3 COMPENSAÇÃO EM ATRASO E EM AVANÇO Bode Diagram Gm = Inf db (at Inf rad/ec), Pm = 34.9 deg (at 2.86 rad/ec) 4 2 Magnitude (db) Phae (deg) Frequency (rad/ec) ( ϕ max = 35 9 arctan ) = Então teremo, α = in in 33.7 =.286 Figura 6: Traçado de bode da planta. reultando z = 5.35 e p = 8.7. Finalmente, da condição G c (j)g p (j) =, obtém-e k = 9., endo o compenador G c () = 9. z A figura 7 apreenta o traçado de Bode de G c ()G p () e também de G p (), endo aí viível a influência do compenador avanço no aumento da margem de fae e da frequência de traveia de ganho. Finalmente apreentam- Bode Diagram Gm = Inf db (at Inf rad/ec), Pm = 45 deg (at rad/ec) 5 Magnitude (db) Phae (deg) Frequency (rad/ec) Figura 7: Traçado de bode do itema compenado. e na figura 8 a repota ao degrau do itema realimentado, com e em compenador, na qual ão víivei a diferença entre a dua ituaçõe. Projecto (para pólo dominante p D, habitualmente complexo):. verificar que G p (p D ) 8 o 9
10 3.2 Compenação avanço 3 COMPENSAÇÃO EM ATRASO E EM AVANÇO Step Repone.4 compenado não compenado.2 Amplitude Time (ec) Figura 8: Repota ao degrau. 2. fazer G c (p D ) = p D+z p D +p = 8o + G p (p D ) 3. ecolher z de modo a cancelar pólo de G p ou da ordem de p D 4. determinar p pela condição de fae 5. determinar k pela condição de módulo k p D+z p D +p G p(p D ) = Exemplo 3.3. Conideremo a planta G p () = (+4), pretendendo-e que o itema em malha fechada tenha pólo em 4 ± 4j. Fazendo p D = 4 + j4, verifica-e que 4 + j4 G p (p D ) = = 35 9 = 225 j4 concluido-e então que devemo ter G c (p D ) = 8 G p (p D ) = = 45. Ecolhendo o zero do compenador de modo a cancelar o ólo da planta em 4, temo z = 4. Então ( ) ( ) 4 + j G c (p D ) = k = 9 arctan 4 + j4 + p p 4 e portanto 9 arctan ( ) 4 = 45 4 p 4 p 4 = tan 45 = p = 8 Finalmente, da condição de módulo temo k ( 4 + j4)( 4 + j4 + 8) = k = = 32 ficando então o compenador G c () =
Compensadores. Controle 1 - DAELN - UTFPR. Os compensadores são utilizados para alterar alguma característica do sistema em malha fechada.
 Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Cap. 8 - Controlador P-I-D
 CONTROLADOR ID Metrado Integrado em Engenharia Electrotécnica e de Comptadore (MEEC) Departamento de Engenharia Electrotécnica e de Comptadore (DEEC) CONTROLO º emetre 7/8 Tranparência de apoio à ala teórica
CONTROLADOR ID Metrado Integrado em Engenharia Electrotécnica e de Comptadore (MEEC) Departamento de Engenharia Electrotécnica e de Comptadore (DEEC) CONTROLO º emetre 7/8 Tranparência de apoio à ala teórica
AÇÕES DE CONTROLE. Ações de Controle Relação Controlador/Planta Controlador proporcional Efeito integral Efeito derivativo Controlador PID
 AÇÕES E CONTROLE Açõe de Controle Relação Controlador/Planta Controlador roorcional Efeito integral Efeito derivativo Controlador PI Controle de Sitema Mecânico - MC - UNICAMP Açõe comun de controle Ação
AÇÕES E CONTROLE Açõe de Controle Relação Controlador/Planta Controlador roorcional Efeito integral Efeito derivativo Controlador PI Controle de Sitema Mecânico - MC - UNICAMP Açõe comun de controle Ação
CONTROLO DE SISTEMAS
 UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
Sistemas a Tempo Discreto - Projeto
 Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
CAPÍTULO 10 Modelagem e resposta de sistemas discretos
 CAPÍTULO 10 Modelagem e repota de itema dicreto 10.1 Introdução O itema dicreto podem er repreentado, do memo modo que o itema contínuo, no domínio do tempo atravé de uma tranformação, nete cao a tranformada
CAPÍTULO 10 Modelagem e repota de itema dicreto 10.1 Introdução O itema dicreto podem er repreentado, do memo modo que o itema contínuo, no domínio do tempo atravé de uma tranformação, nete cao a tranformada
Equações Diferenciais (GMA00112) Resolução de Equações Diferenciais por Séries e Transformada de Laplace
 Equaçõe Diferenciai GMA Reolução de Equaçõe Diferenciai por Série e Tranformada de Laplace Roberto Tocano Couto tocano@im.uff.br Departamento de Matemática Aplicada Univeridade Federal Fluminene Niterói,
Equaçõe Diferenciai GMA Reolução de Equaçõe Diferenciai por Série e Tranformada de Laplace Roberto Tocano Couto tocano@im.uff.br Departamento de Matemática Aplicada Univeridade Federal Fluminene Niterói,
Filtros Analógicos Ativos
 Filtro Analógico Ativo Topologia Sallen-Key FPB Prof. láudio A. Fleury onteúdo. Introdução. Filtro Paa-Baixa de a. Ordem 3. Mudança de Ecala 4. Filtro Paa-Alta de a. Ordem 5. Filtro Paa-Faixa e ejeita-faixa
Filtro Analógico Ativo Topologia Sallen-Key FPB Prof. láudio A. Fleury onteúdo. Introdução. Filtro Paa-Baixa de a. Ordem 3. Mudança de Ecala 4. Filtro Paa-Alta de a. Ordem 5. Filtro Paa-Faixa e ejeita-faixa
CONTROLO DE SISTEMAS. APONTAMENTOS DE MATLAB CONTROL SYSTEM Toolbox. Pedro Dinis Gaspar António Espírito Santo J. A. M.
 UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS APONTAMENTOS DE MATLAB CONTROL SYSTEM Toolbox Pedro Dini Gapar António Epírito Santo J. A. M. Felippe de Souza
UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS APONTAMENTOS DE MATLAB CONTROL SYSTEM Toolbox Pedro Dini Gapar António Epírito Santo J. A. M. Felippe de Souza
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle
 Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA. Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva
 UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
Resolução de Equações Diferenciais Ordinárias por Série de Potências e Transformada de Laplace
 Reolução de Equaçõe Diferenciai Ordinária por Série de Potência e Tranformada de Laplace Roberto Tocano Couto rtocano@id.uff.br Departamento de Matemática Aplicada Univeridade Federal Fluminene Niterói,
Reolução de Equaçõe Diferenciai Ordinária por Série de Potência e Tranformada de Laplace Roberto Tocano Couto rtocano@id.uff.br Departamento de Matemática Aplicada Univeridade Federal Fluminene Niterói,
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO. Professor Leonardo Gonsioroski
 ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
Exercícios Resolvidos de Biofísica
 Exercício Reolvido de Biofíica Faculdade de Medicina da Univeridade de oimbra Exercício Reolvido de Biofíica Metrado ntegrado em Medicina MEMBRNS HOMOGÉNES Exercício 1. Numa experiência com uma membrana
Exercício Reolvido de Biofíica Faculdade de Medicina da Univeridade de oimbra Exercício Reolvido de Biofíica Metrado ntegrado em Medicina MEMBRNS HOMOGÉNES Exercício 1. Numa experiência com uma membrana
Estabilidade para Pequenas Perturbações e Dimensionamento de Estabilizadores. Mestrado em Engenharia Electrotécnica e de Computadores _
 Etabldade para Pequena Perturbaçõe e Dmenonamento de Etablzadore Metrado em Engenhara Electrotécnca e de Computadore _ Dnâmca e Etabldade de Stema de Energa J. A. Peça Lope Conceto Teórco Repreentação
Etabldade para Pequena Perturbaçõe e Dmenonamento de Etablzadore Metrado em Engenhara Electrotécnca e de Computadore _ Dnâmca e Etabldade de Stema de Energa J. A. Peça Lope Conceto Teórco Repreentação
Confrontando Resultados Experimentais e de Simulação
 Confrontando Reultado Experimentai e de Simulação Jorge A. W. Gut Departamento de Engenharia Química Ecola Politécnica da Univeridade de São Paulo E mail: jorgewgut@up.br Um modelo de imulação é uma repreentação
Confrontando Reultado Experimentai e de Simulação Jorge A. W. Gut Departamento de Engenharia Química Ecola Politécnica da Univeridade de São Paulo E mail: jorgewgut@up.br Um modelo de imulação é uma repreentação
Experimento #4. Filtros analógicos ativos LABORATÓRIO DE ELETRÔNICA
 UNIVESIDADE FEDEAL DE CAMPINA GANDE CENTO DE ENGENHAIA ELÉTICA E INFOMÁTICA DEPATAMENTO DE ENGENHAIA ELÉTICA LABOATÓIO DE ELETÔNICA Experimento #4 Filtro analógico ativo EXPEIMENTO #4 Objetivo Gerai Eta
UNIVESIDADE FEDEAL DE CAMPINA GANDE CENTO DE ENGENHAIA ELÉTICA E INFOMÁTICA DEPATAMENTO DE ENGENHAIA ELÉTICA LABOATÓIO DE ELETÔNICA Experimento #4 Filtro analógico ativo EXPEIMENTO #4 Objetivo Gerai Eta
Métodos de Sintonização de Controladores PID
 3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
Universidade Presbiteriana Mackenzie. Controle II
 Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica Controle II Notas de Aula Prof. Marcio Eisencraft Segundo semestre de 004 Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica
Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica Controle II Notas de Aula Prof. Marcio Eisencraft Segundo semestre de 004 Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
 Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Função de Transferência de Malha Fechada
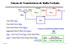 Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Fotografando o Eclipse Total da Lua
 Fotografando o Eclipe Total da Lua (trabalho apreentado para o Mueu de Atronomia e Ciência Afin) http://atrourf.com/diniz/artigo.html Autor: Joé Carlo Diniz (REA-BRASIL) "Você pode e deve fotografar o
Fotografando o Eclipe Total da Lua (trabalho apreentado para o Mueu de Atronomia e Ciência Afin) http://atrourf.com/diniz/artigo.html Autor: Joé Carlo Diniz (REA-BRASIL) "Você pode e deve fotografar o
Projeto do compensador PID no lugar das raízes
 Projeto do compenador PID no lugar da raíze 0 Introdução DAELN - UTFPR - Controle I Paulo Roberto Brero de Campo Neta apotila erão etudado o projeto do compenadore PI, PD e PID atravé do lugar da raíze
Projeto do compenador PID no lugar da raíze 0 Introdução DAELN - UTFPR - Controle I Paulo Roberto Brero de Campo Neta apotila erão etudado o projeto do compenadore PI, PD e PID atravé do lugar da raíze
Newton Maruyama. Projeto de Controladores No Domínio Da Freqüência p. 1/4
 Projeto de Controladores No Domínio Da Freqüência Newton Maruyama Projeto de Controladores No Domínio Da Freqüência p. 1/4 Compensação por avanço de fase Função de Transferência: H(s)=K c α Ts+ 1 αts+
Projeto de Controladores No Domínio Da Freqüência Newton Maruyama Projeto de Controladores No Domínio Da Freqüência p. 1/4 Compensação por avanço de fase Função de Transferência: H(s)=K c α Ts+ 1 αts+
Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional
 Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Sistemas Embarcados. Controladores PI, PD e PID
 Sistemas Embarcados Controladores PI, PD e PID Controladores PI, PD e PID O que são os controladores PI, PD e PID? Aplicações dos controladores Implementação analógica dos controladores Implementação digital
Sistemas Embarcados Controladores PI, PD e PID Controladores PI, PD e PID O que são os controladores PI, PD e PID? Aplicações dos controladores Implementação analógica dos controladores Implementação digital
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG04037 Sistemas de Controle Digitais
 Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Estabilidade no Domínio da Freqüência
 Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Quantas equações existem?
 www2.jatai.ufg.br/oj/index.php/matematica Quanta equaçõe exitem? Rogério Céar do Santo Profeor da UnB - FUP profeorrogeriocear@gmail.com Reumo O trabalho conite em denir a altura de uma equação polinomial
www2.jatai.ufg.br/oj/index.php/matematica Quanta equaçõe exitem? Rogério Céar do Santo Profeor da UnB - FUP profeorrogeriocear@gmail.com Reumo O trabalho conite em denir a altura de uma equação polinomial
ESTUDO DINÂMICO DA PRESSÃO EM VASOS SEPARADORES VERTICAIS GÁS-LÍQUIDO UTILIZADOS NO PROCESSAMENTO PRIMÁRIO DE PETRÓLEO
 ESTUDO DINÂMICO DA PRESSÃO EM VASOS SEPARADORES VERTICAIS GÁS-LÍQUIDO UTILIZADOS NO PROCESSAMENTO PRIMÁRIO DE PETRÓLEO Thale Cainã do Santo Barbalho 1 ; Álvaro Daniel Tele Pinheiro 2 ; Izabelly Laria Luna
ESTUDO DINÂMICO DA PRESSÃO EM VASOS SEPARADORES VERTICAIS GÁS-LÍQUIDO UTILIZADOS NO PROCESSAMENTO PRIMÁRIO DE PETRÓLEO Thale Cainã do Santo Barbalho 1 ; Álvaro Daniel Tele Pinheiro 2 ; Izabelly Laria Luna
Controle de Sistemas. O Método do Lugar das Raízes. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Modelagem Matemática e Simulação computacional de um atuador pneumático considerando o efeito do atrito dinâmico
 Modelagem Matemática e Simulação computacional de um atuador pneumático coniderando o efeito do atrito dinâmico Antonio C. Valdiero, Carla S. Ritter, Luiz A. Raia Depto de Ciência Exata e Engenharia, DCEEng,
Modelagem Matemática e Simulação computacional de um atuador pneumático coniderando o efeito do atrito dinâmico Antonio C. Valdiero, Carla S. Ritter, Luiz A. Raia Depto de Ciência Exata e Engenharia, DCEEng,
Projeto de sistemas de controle
 Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
LABORATÓRIO DE CONTROLE I APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM
 UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
PROCEDIMENTO DE MERCADO AM.04 Cálculo de Votos e Contribuição
 PROCEDIMENTO DE MERCADO AM.04 Cálculo de Voto e Contribuição Reponável pelo PM: Acompanhamento do Mercado CONTROLE DE ALTERAÇÕES Verão Data Decrição da Alteração Elaborada por Aprovada por PM AM.04 - Cálculo
PROCEDIMENTO DE MERCADO AM.04 Cálculo de Voto e Contribuição Reponável pelo PM: Acompanhamento do Mercado CONTROLE DE ALTERAÇÕES Verão Data Decrição da Alteração Elaborada por Aprovada por PM AM.04 - Cálculo
Análise de Sensibilidade de Anemômetros a Temperatura Constante Baseados em Sensores Termo-resistivos
 UNIVERSIDADE FEDERAL DO MARANHÃO CENTRO DE CIÊNCIA E TECNOLOGIA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA DE ELETRICIDADE Análie de Senibilidade de Anemômetro a Temperatura Contante Baeado em Senore Termo-reitivo
UNIVERSIDADE FEDERAL DO MARANHÃO CENTRO DE CIÊNCIA E TECNOLOGIA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA DE ELETRICIDADE Análie de Senibilidade de Anemômetro a Temperatura Contante Baeado em Senore Termo-reitivo
Estudo Experimental da Erosão Localizada na Proximidade de Pilares de Pontes. Maria Manuela C. Lemos Lima 1
 Etudo Experimental da Eroão Localizada na Proximidade de Pilare de Ponte Maria Manuela C. Lemo Lima 1 Univeridade do Minho, epartamento de Engenharia Civil Azurém, P 4800-058 Guimarãe, Portugal RESUMO
Etudo Experimental da Eroão Localizada na Proximidade de Pilare de Ponte Maria Manuela C. Lemo Lima 1 Univeridade do Minho, epartamento de Engenharia Civil Azurém, P 4800-058 Guimarãe, Portugal RESUMO
Capítulo 3 Sistemas de Controle com Realimentação
 Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Introdução AVALIAÇÃO DE DESEMPENHO. No domínio do tempo. No domínio da freqüência. Função de transferência. Módulo e fase da função de transferência
 AVALIAÇÃO DE DESEMPENHO Introdução Introdução Análise no domínio do tempo Resposta ao degrau Resposta à rampa Aula anterior Resposta à parábola Análise no domínio da freqüência Diagramas de Bode Diagrama
AVALIAÇÃO DE DESEMPENHO Introdução Introdução Análise no domínio do tempo Resposta ao degrau Resposta à rampa Aula anterior Resposta à parábola Análise no domínio da freqüência Diagramas de Bode Diagrama
Díodo de Junção Semicondutora
 íodo de Junção emicondutora ispositivos Eletrónicos Licenciatura em Engenharia Electrónica C. Ferreira Fernandes 2012-13 Laboratório de ispositivos Electrónicos ÍOO E JUNÇÃO Material utilizado: Placa de
íodo de Junção emicondutora ispositivos Eletrónicos Licenciatura em Engenharia Electrónica C. Ferreira Fernandes 2012-13 Laboratório de ispositivos Electrónicos ÍOO E JUNÇÃO Material utilizado: Placa de
Resistência dos Materiais SUMÁRIO 1. TENSÕES DE CISALHAMENTO... 1 1.1 DIMENSIONAMENTO... 2 1.2 EXEMPLOS... 2
 Reitência do Materiai SUMÁRIO 1. TESÕES DE CISLHMETO... 1 1.1 DIMESIOMETO... 1. EXEMPLOS... Cialhamento 0 Prof. Joé Carlo Morilla Reitência do Materiai 1. Tenõe de Cialhamento Quando dua força cortante
Reitência do Materiai SUMÁRIO 1. TESÕES DE CISLHMETO... 1 1.1 DIMESIOMETO... 1. EXEMPLOS... Cialhamento 0 Prof. Joé Carlo Morilla Reitência do Materiai 1. Tenõe de Cialhamento Quando dua força cortante
Livro para a SBEA (material em construção) Edmundo Rodrigues 9. peneiras
 Livro para a SBEA (material em contrução) Edmundo Rodrigue 9 4.1. Análie granulométrica Granulometria, graduação ou compoição granulométrica de um agregado é a ditribuição percentual do eu divero tamanho
Livro para a SBEA (material em contrução) Edmundo Rodrigue 9 4.1. Análie granulométrica Granulometria, graduação ou compoição granulométrica de um agregado é a ditribuição percentual do eu divero tamanho
CAP. 3 - EXTENSÔMETROS - "STRAIN GAGES" Exemplo: extensômetro Huggenberger
 CAP. 3 - EXTENSÔMETOS - "STAIN GAGES" 3. - Extensômetros Mecânicos Exemplo: extensômetro Huggenberger Baseia-se na multiplicação do deslocamento através de mecanismos de alavancas. Da figura: l' = (w /
CAP. 3 - EXTENSÔMETOS - "STAIN GAGES" 3. - Extensômetros Mecânicos Exemplo: extensômetro Huggenberger Baseia-se na multiplicação do deslocamento através de mecanismos de alavancas. Da figura: l' = (w /
EXPERIÊNCIA 7 CONVERSORES PARA ACIONAMENTO DE MÁQUINAS ELÉTRICAS
 FACULDADE DE ENGENHARIA ELÉTRICA E DE COMPUTAÇÃO - UNICAMP EE-832 - LABORATÓRIO DE ELETRÔNICA INDUSTRIAL EXPERIÊNCIA 7 CONVERSORES PARA ACIONAMENTO DE MÁQUINAS ELÉTRICAS 7. Introdução A máquina de corrente
FACULDADE DE ENGENHARIA ELÉTRICA E DE COMPUTAÇÃO - UNICAMP EE-832 - LABORATÓRIO DE ELETRÔNICA INDUSTRIAL EXPERIÊNCIA 7 CONVERSORES PARA ACIONAMENTO DE MÁQUINAS ELÉTRICAS 7. Introdução A máquina de corrente
Capítulo 5: Análise através de volume de controle
 Capítulo 5: Análie atravé de volume de controle Volume de controle Conervação de maa Introdução Exite um fluxo de maa da ubtância de trabalho em cada equipamento deta uina, ou eja, na bomba, caldeira,
Capítulo 5: Análie atravé de volume de controle Volume de controle Conervação de maa Introdução Exite um fluxo de maa da ubtância de trabalho em cada equipamento deta uina, ou eja, na bomba, caldeira,
Prova 2 - Sistemas de Controle Projetos
 Prova - Sistemas de Controle Projetos Pedro Batista (887) - pedro@ufpa.br Paulo Victor Mocbel (887) - pvmocbel@gmail.com December 4, Projeto de Controlador PI ideal Desejamos adicionar um controlador proporcional
Prova - Sistemas de Controle Projetos Pedro Batista (887) - pedro@ufpa.br Paulo Victor Mocbel (887) - pvmocbel@gmail.com December 4, Projeto de Controlador PI ideal Desejamos adicionar um controlador proporcional
Introdução ao Estudo da Corrente Eléctrica
 Introdução ao Estudo da Corrente Eléctrica Num metal os electrões de condução estão dissociados dos seus átomos de origem passando a ser partilhados por todos os iões positivos do sólido, e constituem
Introdução ao Estudo da Corrente Eléctrica Num metal os electrões de condução estão dissociados dos seus átomos de origem passando a ser partilhados por todos os iões positivos do sólido, e constituem
Controle II. Estudo e sintonia de controladores industriais
 Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Modelação e Simulação Problemas - 4
 Modelação e Simulação - Problema Modelação e Simulação Problema - P. Para cada uma da funçõe de tranferência eguinte eboce qualitativamente a repota no tempo ao ecalão unitário uando empre que aplicável)
Modelação e Simulação - Problema Modelação e Simulação Problema - P. Para cada uma da funçõe de tranferência eguinte eboce qualitativamente a repota no tempo ao ecalão unitário uando empre que aplicável)
TRANSFORMADORES DE POTENCIAL
 TRANSFORMADORES DE POTENCIA 1 - Introdução: Tio de TP TP Eletromagnético (TP) TP Caacitivo (TPC) Até 138 k Acima de 138 k Funçõe Báica - Iolamento contra alta tenõe. - Fornecimento no ecundário de uma
TRANSFORMADORES DE POTENCIA 1 - Introdução: Tio de TP TP Eletromagnético (TP) TP Caacitivo (TPC) Até 138 k Acima de 138 k Funçõe Báica - Iolamento contra alta tenõe. - Fornecimento no ecundário de uma
Um exemplo de Análise de Covariância. Um exemplo de Análise de Covariância (cont.)
 Um exemplo de Análie de Covariância A Regreão Linear e a Análie de Variância etudada até aqui, ão cao particulare do Modelo Linear, que inclui também a Análie de Covariância Em qualquer deta trê ituaçõe
Um exemplo de Análie de Covariância A Regreão Linear e a Análie de Variância etudada até aqui, ão cao particulare do Modelo Linear, que inclui também a Análie de Covariância Em qualquer deta trê ituaçõe
Circuitos de 2 ª ordem: RLC. Parte 1
 Circuitos de 2 ª ordem: RLC Parte 1 Resposta natural de um circuito RLC paralelo Veja circuito RLC paralelo abaixo: A tensão é a mesma e aplicando a soma de correntes que saem do nó superior temos: v R
Circuitos de 2 ª ordem: RLC Parte 1 Resposta natural de um circuito RLC paralelo Veja circuito RLC paralelo abaixo: A tensão é a mesma e aplicando a soma de correntes que saem do nó superior temos: v R
Lista de exercícios 2 Resposta no Tempo, Erros Estacionários e Lugar Geométrico das Raízes
 16003 Controle Dinâmico ENE - UnB Lita de exercício 16003 Controle Dinâmico o emetre de 01 Lita de exercício Repota no Tempo, Erro Etacionário e Lugar Geométrico da Raíze 1. Quando o itema motrado na figura
16003 Controle Dinâmico ENE - UnB Lita de exercício 16003 Controle Dinâmico o emetre de 01 Lita de exercício Repota no Tempo, Erro Etacionário e Lugar Geométrico da Raíze 1. Quando o itema motrado na figura
SISTEMAS DE CONTROLE II
 SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
Apostila de SINAIS E SISTEMAS
 Apotila de SINAIS E SISTEMAS Álvaro Luiz Stelle (PhD) DAELN CPGEI CEFET PR Março de 5 I PREFÁCIO Eta apotila tem como objetivo dar ao leitor um embaamento teórico da Tranformada de Laplace, de Fourier
Apotila de SINAIS E SISTEMAS Álvaro Luiz Stelle (PhD) DAELN CPGEI CEFET PR Março de 5 I PREFÁCIO Eta apotila tem como objetivo dar ao leitor um embaamento teórico da Tranformada de Laplace, de Fourier
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade
 Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Capítulo I Tensões. Seja um corpo sob a ação de esforços externos em equilíbrio, como mostra a figura I-1:
 apítuo I Seja um corpo ob a ação de eforço externo em equiíbrio, como motra a figura I-1: Figura I-3 Eforço que atuam na eção para equiibrar o corpo Tome-e, agora, uma pequena área que contém o ponto,
apítuo I Seja um corpo ob a ação de eforço externo em equiíbrio, como motra a figura I-1: Figura I-3 Eforço que atuam na eção para equiibrar o corpo Tome-e, agora, uma pequena área que contém o ponto,
Sistemas e Sinais 2009/2010
 Análie de Sitema alimentado Sitema e Sinai 9/ Análie de itema realimentado Álgebra de diagrama de bloco Sitema realimentado Etabilidade Deempenho SSin Diagrama de bloco Sitema em érie X Y G G Z Y G X Z
Análie de Sitema alimentado Sitema e Sinai 9/ Análie de itema realimentado Álgebra de diagrama de bloco Sitema realimentado Etabilidade Deempenho SSin Diagrama de bloco Sitema em érie X Y G G Z Y G X Z
I Controle Contínuo 1
 Sumário I Controle Contínuo 1 1 Introdução 3 11 Sistemas de Controle em Malha Aberta e em Malha Fechada 5 12 Componentes de um sistema de controle 5 13 Comparação de Sistemas de Controle em Malha Aberta
Sumário I Controle Contínuo 1 1 Introdução 3 11 Sistemas de Controle em Malha Aberta e em Malha Fechada 5 12 Componentes de um sistema de controle 5 13 Comparação de Sistemas de Controle em Malha Aberta
Nestas notas será analisado o comportamento deste motor em regime permanente.
 MOTO DE INDUÇÃO TIFÁSICO 8/0/006 Ivan Camargo Introdução O motor de indução trifáico correponde a, aproximadamente, 5 % da carga elétrica do Brail, ou eja, 50 % da carga indutrial que, por ua vez, correponde
MOTO DE INDUÇÃO TIFÁSICO 8/0/006 Ivan Camargo Introdução O motor de indução trifáico correponde a, aproximadamente, 5 % da carga elétrica do Brail, ou eja, 50 % da carga indutrial que, por ua vez, correponde
3º ano 1º semestre 2007/2008
 Metrado Integrado em Engenharia Electrotécnica e de Computadore (LEEC) Departamento de Engenharia Electrotécnica e de Computadore (DEEC) CONROLO 3º ano º emetre 2007/2008 ranparência de apoio à aula teórica
Metrado Integrado em Engenharia Electrotécnica e de Computadore (LEEC) Departamento de Engenharia Electrotécnica e de Computadore (DEEC) CONROLO 3º ano º emetre 2007/2008 ranparência de apoio à aula teórica
Palavras-chave:Algoritmo Genético; Carregamento de Contêiner; Otimização Combinatória.
 Reolução do Problema de Carregamento e Decarregamento 3D de Contêinere em Terminai Portuário para Múltiplo Cenário via Repreentação por Regra e Algoritmo Genético Aníbal Tavare de Azevedo (UNICAMP) anibal.azevedo@fca.unicamp.br
Reolução do Problema de Carregamento e Decarregamento 3D de Contêinere em Terminai Portuário para Múltiplo Cenário via Repreentação por Regra e Algoritmo Genético Aníbal Tavare de Azevedo (UNICAMP) anibal.azevedo@fca.unicamp.br
Aula 7 Resposta no domínio do tempo - Sistemas de segunda ordem
 FUNDAMENTOS DE CONTROLE E AUTOMAÇÃO Aula 7 Repota no domínio do tempo - Sitema de egunda ordem Prof. Marcio Kimpara Univeridade Federal de Mato Groo do Sul Sitema de primeira ordem Prof. Marcio Kimpara
FUNDAMENTOS DE CONTROLE E AUTOMAÇÃO Aula 7 Repota no domínio do tempo - Sitema de egunda ordem Prof. Marcio Kimpara Univeridade Federal de Mato Groo do Sul Sitema de primeira ordem Prof. Marcio Kimpara
INTRODUÇÃO CARACTERÍSTICAS
 FILTROS ATIVOS INTRODUÇÃO Circuitos importantes em sistemas de comunicação e instrumentação; Área vasta da eletrônica conceitos fundamentais; Conjunto de modelos de filtros e métodos de projetos; CARACTERÍSTICAS
FILTROS ATIVOS INTRODUÇÃO Circuitos importantes em sistemas de comunicação e instrumentação; Área vasta da eletrônica conceitos fundamentais; Conjunto de modelos de filtros e métodos de projetos; CARACTERÍSTICAS
Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP. Prof. Cassiano Rech cassiano@ieee.org
 Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP cassiano@ieee.org 1 Operação como PFP Como a freqüência de comutação do interruptor S é muito maior que a freqüência
Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP cassiano@ieee.org 1 Operação como PFP Como a freqüência de comutação do interruptor S é muito maior que a freqüência
CAPÍTULO 12. Projeto de controladores discretos
 CAPÍULO 2 Projeto de controladores discretos 2. Introdução O projeto de controladores discretos pode ser realizado por emulaçào, onde um controlador contínuo é projetado, usando as mesmas técnicas vistas
CAPÍULO 2 Projeto de controladores discretos 2. Introdução O projeto de controladores discretos pode ser realizado por emulaçào, onde um controlador contínuo é projetado, usando as mesmas técnicas vistas
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica
 UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
Curso de Instrumentista de Sistemas. Fundamentos de Controle. Prof. Msc. Jean Carlos
 Curso de Instrumentista de Sistemas Fundamentos de Controle Prof. Msc. Jean Carlos Ações de controle em malha fechada Controle automático contínuo em malha fechada Ação proporcional A característica da
Curso de Instrumentista de Sistemas Fundamentos de Controle Prof. Msc. Jean Carlos Ações de controle em malha fechada Controle automático contínuo em malha fechada Ação proporcional A característica da
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS RESPOSTA DE ELEMENTOS PRIMÁRIOS
 INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS RESPOSTA DE ELEMENTOS PRIMÁRIOS Introdução As características dinâmicas de um instrumento de medição podem ser determinadas estudando-se o sistema físico, e escrevendo-se
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS RESPOSTA DE ELEMENTOS PRIMÁRIOS Introdução As características dinâmicas de um instrumento de medição podem ser determinadas estudando-se o sistema físico, e escrevendo-se
RECORRÊNCIAS DO TIPO FIBONACCI E APLICAÇÕES
 RECORRÊNCIAS DO TIPO FIBONACCI E APLICAÇÕES JOSÉ H. DA CRUZ, MARINA T. MIZUKOSHI E RONALDO A. DOS SANTOS Reumo. O cláico problema envolvendo populaçõe de coelho propoto por Fibonacci em 1202 foi a bae
RECORRÊNCIAS DO TIPO FIBONACCI E APLICAÇÕES JOSÉ H. DA CRUZ, MARINA T. MIZUKOSHI E RONALDO A. DOS SANTOS Reumo. O cláico problema envolvendo populaçõe de coelho propoto por Fibonacci em 1202 foi a bae
A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte:
 Processo A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte: K=26.4 Ganho L=203 Atraso em ms τ=334 Constante de tempo em ms.
Processo A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte: K=26.4 Ganho L=203 Atraso em ms τ=334 Constante de tempo em ms.
Aula 8 Controladores do tipo Proporcional, Integral e Diferencial
 Aula 8 Controladores do tipo Proporcional, Integral e Diferencial Introdução Estrutura do Controlador PID Efeito da Ação Proporcional Efeito da Ação Integral Efeito da Ação Derivativa Sintonia de Controladores
Aula 8 Controladores do tipo Proporcional, Integral e Diferencial Introdução Estrutura do Controlador PID Efeito da Ação Proporcional Efeito da Ação Integral Efeito da Ação Derivativa Sintonia de Controladores
Vibrações Mecânicas. Vibração Livre Sistemas com 1 GL. Ramiro Brito Willmersdorf ramiro@willmersdorf.net
 Vibrações Mecânicas Vibração Livre Sistemas com 1 GL Ramiro Brito Willmersdorf ramiro@willmersdorf.net Departamento de Engenharia Mecânica Universidade Federal de Pernambuco 2015.1 Introdução Modelo 1
Vibrações Mecânicas Vibração Livre Sistemas com 1 GL Ramiro Brito Willmersdorf ramiro@willmersdorf.net Departamento de Engenharia Mecânica Universidade Federal de Pernambuco 2015.1 Introdução Modelo 1
8- Controlador PID. PID = Proporcional + Integral + Derivativo
 Controlaor PID 154 8- Controlaor PID PID = Proporcional + Integral + Derivativo É interessante assinalar que mais a metae os controlaores inustriais em uso nos ias atuais utiliza estratégias e controle
Controlaor PID 154 8- Controlaor PID PID = Proporcional + Integral + Derivativo É interessante assinalar que mais a metae os controlaores inustriais em uso nos ias atuais utiliza estratégias e controle
Me todos de Ajuste de Controladores
 Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
4. Conversores de corrente continua-corrente contínua com isolamento
 onversores com isolamento galvânico 4. onversores de corrente continuacorrente contínua com isolamento Exercício nº4.1 Pretendese dimensionar um conversor redutor com isolamento galvânico para controlar
onversores com isolamento galvânico 4. onversores de corrente continuacorrente contínua com isolamento Exercício nº4.1 Pretendese dimensionar um conversor redutor com isolamento galvânico para controlar
Ficha 8 Aplicação de conceitos em MatLab
 U N I V E R S I D A D E D A B E I R A I N T E R I O R Departamento de Engenharia Electromecânica CONTROLO DISCRETO E DIGITAL (Prática/Laboratorial) Ficha 8 Aplicação de conceito em MatLab Todo o exercício
U N I V E R S I D A D E D A B E I R A I N T E R I O R Departamento de Engenharia Electromecânica CONTROLO DISCRETO E DIGITAL (Prática/Laboratorial) Ficha 8 Aplicação de conceito em MatLab Todo o exercício
A notação utilizada na teoria das filas é variada mas, em geral, as seguintes são comuns:
 A notação utilizada na teoria da fila é variada ma, em geral, a eguinte ão comun: λ número médio de cliente que entram no itema or unidade de temo; µ número médio de cliente atendido (que aem do itema)
A notação utilizada na teoria da fila é variada ma, em geral, a eguinte ão comun: λ número médio de cliente que entram no itema or unidade de temo; µ número médio de cliente atendido (que aem do itema)
Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores. Controlo 2005/2006. Controlo de velocidade de um motor D.C.
 Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores Controlo 2005/2006 Controlo de velocidade de um motor D.C. Elaborado por E. Morgado 1 e F. M. Garcia 2 Reformulado
Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores Controlo 2005/2006 Controlo de velocidade de um motor D.C. Elaborado por E. Morgado 1 e F. M. Garcia 2 Reformulado
RESISTÊNCIA E PROPULSÃO Mestrado em Engenharia e Arquitectura Naval Exame de 2ª Época 26 de Janeiro de 2010 Duração: 3 horas
 RESISTÊNCIA E PROPULSÃO Metrado e Engenharia e Arquitectura Naval Exae de ª Época 6 de Janeiro de 010 Duração: 3 hora Quetão 1. U porta-contentore te a eguinte caracterítica: -Superfície olhada: 5454.
RESISTÊNCIA E PROPULSÃO Metrado e Engenharia e Arquitectura Naval Exae de ª Época 6 de Janeiro de 010 Duração: 3 hora Quetão 1. U porta-contentore te a eguinte caracterítica: -Superfície olhada: 5454.
Enunciados de Problemas
 INSTITUTO SUPERIOR TÉCNICO LICENCIATURA EM ENGENHARIA ELECTROTÉCNICA E DE COMPUTADORES Enunciados de Problemas de Sistemas de Telecomunicações I Ano Lectivo de 2002/2003 2.17 Admita que o coeficiente de
INSTITUTO SUPERIOR TÉCNICO LICENCIATURA EM ENGENHARIA ELECTROTÉCNICA E DE COMPUTADORES Enunciados de Problemas de Sistemas de Telecomunicações I Ano Lectivo de 2002/2003 2.17 Admita que o coeficiente de
13 a Aula 2004.10.13 AMIV LEAN, LEC Apontamentos
 3 a Aula 2004.0.3 AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 3. Singularidades isoladas Para na prática podermos aplicar o teorema dos resíduos com eficiência, precisamos de conhecer
3 a Aula 2004.0.3 AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 3. Singularidades isoladas Para na prática podermos aplicar o teorema dos resíduos com eficiência, precisamos de conhecer
CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA DE SÃO PAULO CEFET SP
 Diciplina: Mecânica do Fluido Aplicada Lita de Exercício Reolvido Profeor: 1 de 11 Data: 13/0/08 Caruo 1. Um menino, na tentativa de melhor conhecer o fundo do mar, pretende chegar a uma profundidade de
Diciplina: Mecânica do Fluido Aplicada Lita de Exercício Reolvido Profeor: 1 de 11 Data: 13/0/08 Caruo 1. Um menino, na tentativa de melhor conhecer o fundo do mar, pretende chegar a uma profundidade de
SITE EM JAVA PARA A SIMULAÇÃO DE MÁQUINAS ELÉTRICAS
 SITE EM JAVA PARA A SIMULAÇÃO DE MÁQUINAS ELÉTRICAS Reumo Luca Franco de Ai¹ Marcelo Semenato² ¹Intituto Federal de Educação, Ciência e Tecnologia/Campu Jataí/Engenharia Elétrica/PIBIT-CNPQ lucafranco_jty@hotmail.com
SITE EM JAVA PARA A SIMULAÇÃO DE MÁQUINAS ELÉTRICAS Reumo Luca Franco de Ai¹ Marcelo Semenato² ¹Intituto Federal de Educação, Ciência e Tecnologia/Campu Jataí/Engenharia Elétrica/PIBIT-CNPQ lucafranco_jty@hotmail.com
= T B. = T Bloco A: F = m. = P Btang. s P A. 3. b. P x. Bloco B: = 2T s T = P B 2 s. s T = m 10 B 2. De (I) e (II): 6,8 m A. s m B
 eolução Fíica FM.9 1. e Com bae na tabela, obervamo que o atleta etá com 5 kg acima do peo ideal. No gráfico, temo, para a meia maratona: 1 kg,7 min 5 kg x x,5 min. Na configuração apreentada, a força
eolução Fíica FM.9 1. e Com bae na tabela, obervamo que o atleta etá com 5 kg acima do peo ideal. No gráfico, temo, para a meia maratona: 1 kg,7 min 5 kg x x,5 min. Na configuração apreentada, a força
p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem
 p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem Introdução Os primeiros filtros construídos eram circuitos LC passivos.
p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem Introdução Os primeiros filtros construídos eram circuitos LC passivos.
Máquinas Eléctricas. Motores de indução. Motores assíncronos. Arranque
 Motore de indução Arranque São motore robuto e barato (fabricado em maa), embora tendo o inconveniente de não erem regulávei. Conequentemente, uma vez definido um binário e uma corrente, ete apena dependem
Motore de indução Arranque São motore robuto e barato (fabricado em maa), embora tendo o inconveniente de não erem regulávei. Conequentemente, uma vez definido um binário e uma corrente, ete apena dependem
Resposta em Frequência
 Resposta em Frequência G( s) = s 2 1 +,5s + 1 2 2.5 Nyquist Diagram 2-2 -4-6 -8 Imaginary Axis 1.5 1.5 -.5-9 -1-1.5-2 -18 1-2 1-1 1 1 1 1 2 Frequency (rad/sec) -2.5-1 -.5.5 1 1.5 Real Axis 1 Mapeamento
Resposta em Frequência G( s) = s 2 1 +,5s + 1 2 2.5 Nyquist Diagram 2-2 -4-6 -8 Imaginary Axis 1.5 1.5 -.5-9 -1-1.5-2 -18 1-2 1-1 1 1 1 1 2 Frequency (rad/sec) -2.5-1 -.5.5 1 1.5 Real Axis 1 Mapeamento
Datas Importantes 2013/01
 INSTRUMENTAÇÃO CARACTERÍSTICAS DE UM SISTEMA DE MEDIÇÃO PROBABILIDADE PROPAGAÇÃO DE INCERTEZA MÍNIMOS QUADRADOS Instrumentação - Profs. Isaac Silva - Filipi Vianna - Felipe Dalla Vecchia 2013 Datas Importantes
INSTRUMENTAÇÃO CARACTERÍSTICAS DE UM SISTEMA DE MEDIÇÃO PROBABILIDADE PROPAGAÇÃO DE INCERTEZA MÍNIMOS QUADRADOS Instrumentação - Profs. Isaac Silva - Filipi Vianna - Felipe Dalla Vecchia 2013 Datas Importantes
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO
 João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
Aula 07 Análise no domínio do tempo Parte II Sistemas de 2ª ordem
 Aula 07 Aálise o domíio do tempo Parte II Sistemas de ª ordem Aálise o domíio do tempo - Sistemas de ª ordem iput S output Sistema de seguda ordem do tipo α G(s) as + bs + c Aálise o domíio do tempo -
Aula 07 Aálise o domíio do tempo Parte II Sistemas de ª ordem Aálise o domíio do tempo - Sistemas de ª ordem iput S output Sistema de seguda ordem do tipo α G(s) as + bs + c Aálise o domíio do tempo -
Verificação e Validação em CFD
 Erro de arredondamento. Erro iterativo. Erro de discretização. As três componentes do erro numérico têm comportamentos diferentes com o aumento do número de graus de liberdade (refinamento da malha). Erro
Erro de arredondamento. Erro iterativo. Erro de discretização. As três componentes do erro numérico têm comportamentos diferentes com o aumento do número de graus de liberdade (refinamento da malha). Erro
PRINCÍPIOS DA CORRENTE ALTERNADA PARTE 1. Adrielle C. Santana
 PRINCÍPIOS DA CORRENTE ALTERNADA PARTE 1 Adrielle C. Santana Vantagem da Corrente Alternada O uso da corrente contínua tem suas vantagens, como por exemplo, a facilidade de controle de velocidade de motores
PRINCÍPIOS DA CORRENTE ALTERNADA PARTE 1 Adrielle C. Santana Vantagem da Corrente Alternada O uso da corrente contínua tem suas vantagens, como por exemplo, a facilidade de controle de velocidade de motores
AVALIAÇÃO DE DESEMPENHO
 AVALIAÇÃO DE DESEMPENHO Itrodução Aálie o domíio do tempo Repota ao degrau Repota à rampa Repota à parábola Aálie o domíio da freqüêcia Diagrama de Bode Diagrama de Nyquit Diagrama de Nichol Eta aula EM
AVALIAÇÃO DE DESEMPENHO Itrodução Aálie o domíio do tempo Repota ao degrau Repota à rampa Repota à parábola Aálie o domíio da freqüêcia Diagrama de Bode Diagrama de Nyquit Diagrama de Nichol Eta aula EM
Matemática para Engenharia
 Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO
 João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1 EM COMPUTADOR DE UM PROJETO...1
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1 EM COMPUTADOR DE UM PROJETO...1
Aula 1 Introdução. Análise de redes em condições transitórias. rias:
 Proteção de Sistemas Elétricos Aula 1 Introdução Análise de redes em condições transitórias condições transitórias: rias: chaveamento CC falta de fase formas de ondas anormais descargas atmosféricas origem:
Proteção de Sistemas Elétricos Aula 1 Introdução Análise de redes em condições transitórias condições transitórias: rias: chaveamento CC falta de fase formas de ondas anormais descargas atmosféricas origem:
INSTRUMENTAÇÃO. Eng. Marcelo Saraiva Coelho
 INSTRUMENTAÇÃO CONCEITOS E DEFINIÇÕES Nas indústrias, o termo PROCESSO tem um significado amplo. Uma operação unitária, como por exemplo, destilação, filtração ou aquecimento, é considerado um PROCESSO.
INSTRUMENTAÇÃO CONCEITOS E DEFINIÇÕES Nas indústrias, o termo PROCESSO tem um significado amplo. Uma operação unitária, como por exemplo, destilação, filtração ou aquecimento, é considerado um PROCESSO.
