[ \ x Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \.
|
|
|
- Edite Osório Gesser
- 8 Há anos
- Visualizações:
Transcrição
1 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV1 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV Å 1Ro}HV *HUDLV Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \. [\ [\ É fácil verificar que este sistema tem como ~QLFDVROXomR, [ \ Em termos gráficos, as equações representam duas UHFWDV no plano, cujo SRQWR GHLQWHUVHFomR é a VROXomRGRVLVWHPD. Contudo, sabemos também que QHPWRGRVRVVLVWHPDVOLQHDUHVWrPVROXomR. Como por eemplo, [\ [\
2 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV2 Graficamente, isso acontece porque as duas HTXDo}HVOLQHDUHV representam duas UHFWDVSDUDOHODV. Pode ainda acontecer que o sistema seja possível, mas WHQKDXPDLQILQLGDGH GHVROXo}HV. Como por eemplo, [\ [\ Graficamente, isso acontece porque as duas equações representam efectivamente D PHVPDUHFWD. A solução do sistema é o conjunto de todos os pontos dessa recta. Para tentar resolver sistemas de dimensões superiores, precisamos de matrizes.
3 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV3 Å 6LVWHPDV H 0DWUL]HV Uma HTXDomROLQHDU tem a forma geral, onde, D L, L {Q} são os FRHILFLHQWHV [ L, L {Q} as LQFyJQLWDV E o WHUPRLQGHSHQGHQWH Uma equação linear pode ser representada na sua IRUPDPDWULFLDO, PDWUL]OLQKDGRVFRHILFLHQWHV PDWUL]FROXQDGDVLQFyJQLWDV Dizemos que o n-uplo V V V Q éuma VROXomRGDHTXDomROLQHDU se,
4 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV4 Na forma matricial, é uma matriz coluna tal que, Ao conjunto de todas as soluções chamamos FRQMXQWRVROXomR da equação linear. Por eemplo, com =, consideremos a HTXDomROLQHDU, com UHSUHVHQWDomRPDWULFLDO, Eplicitando em função de uma das incógnitas, por eemplo [, podemos formalizar o FRQMXQWRVROXomR como, ou seja, WRGRVRVWHUQRV [ [ [ tais que [ [ [ ±, como por eemplo: Para obter uma VROXomR~QLFD seriam necessárias três equações lineares...
5 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV5 Å 6LVWHPDV GH (TXDo}HV /LQHDUHV Um VLVWHPDGHP HTXDo}HVOLQHDUHV e Q LQFyJQLWDV, P, Q, tem a forma geral, onde, D LM, L {P} e M {Q} são os FRHILFLHQWHV [ M, M {Q} são as LQFyJQLWDV E L, L {P} são os WHUPRVLQGHSHQGHQWHV Se E L para WRGR o L {P} o sistema diz-se KRPRJpQHR, caso contrário o sistema diz-se FRPSOHWR. O n-uplo V V V Q é uma VROXomRGRVLVWHPD se for solução de todas as equações do sistema. Ao conjunto de todas as soluções chamamos FRQMXQWRVROXomR do sistema. Por eemplo, [ [ [ [ [ [ é um sistema completo, de 2 equações e 3 incógnitas.
6 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV6 O terno é XPD VROXomR do sistema pois, l l l l l l Dois sistemas são HTXLYDOHQWHV se tiverem o mesmo conjunto solução. Uma RSHUDomRHOHPHQWDU transforma um dado sistema noutro que lhe é equivalente. > 2SHUDo}HV HOHPHQWDUHV Representamos as equações do sistema por H L com L {P}. 7URFDUGXDVHTXDo}HV H L Ž H M 0XOWLSOLFDUXPDHTXDomRSRUXPHVFDODUQmRQXOR H L ~DH L com D $GLFLRQDUDXPDHTXDomRRXWUDPXOWLSOLFDGDSRUXPHVFDODU H L ~ H L + E H M Aplicando uma sequência de operações elementares a um dado sistema, obtemos outro sistema com o mesmo conjunto solução. Deste modo podemos transformar um dado sistema linear noutro, cuja resolução é mais simples.
7 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV7 Por eemplo para o sistema, [\ [\ H ~ - H [\ [\ H ~ H H [\ \ H ~ òh [\ \ H ~ H H [ \ H ~ ò H [ \ Assim, por uma sequência de operações elementares obtivemos um sistema equivalente, ou seja, a VROXomR~QLFD do sistema inicial, [ \
8 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV8 Por eemplo para o sistema, [ [ [ [ [ [ [ [ H ~ H H [ [ [ [ [ [ [ H ~ H H [ [ [ [ [ [ [ H ~ H òh [ [ [ [ [ ò[ ò Deste modo, obtivemos um VLVWHPDHTXLYDOHQWH onde é óbvio que [. Mas, conhecido este valor, podemos substituí-lo na segunda equação, [ donde, [ E conhecidos os valores de [ e [ podemos substituí-los na primeira equação, [ donde, [
9 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV9 O sistema anterior tem portanto como ~QLFDVROXomR o terno. Ou seja, o FRQMXQWRVROXomR ^ ` é unitário. Atendendo ao Q~PHURGHVROXo}HV, um sistema de equações lineares pode ser classificado como: LPSRVVtYHO quando não tem solução SRVVtYHOHGHWHUPLQDGR quando tem uma única solução SRVVtYHO SRVVtYHOHLQGHWHUPLQDGR quando tem uma infinidade de soluções Por eemplo o sistema de equações e incógnitas,
10 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV10 Assim, o conjunto solução deste sistema é dado por, Trata-se portanto de um VLVWHPDSRVVtYHOHLQGHWHUPLQDGR, pois todo e qualquer valor real da variável [ gera uma solução. Dizemos que [ éuma YDULiYHOOLYUH na solução. Num sistema possível e indeterminado chama-se JUDXGHLQGHWHUPLQDomR ao número de variáveis livres nas soluções. O sistema anterior tem XPD~QLFDYDULiYHOOLYUH, pelo que o JUDXGH LQGHWHUPLQDomRé igual a. Por eemplo o sistema de equações e incógnitas, Trata-se portanto de um VLVWHPDLPSRVVtYHO e o conjunto solução é vazio. Para uma maior comodidade dos cálculos das operações elementares e para permitir a sua programação, os sistemas de maiores dimensões são habitualmente representados na sua forma matricial.
11 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV11 Å 5HSUHVHQWDomR 0DWULFLDO GH 6LVWHPDV GH (TXDo}HV /LQHDUHV Um dado VLVWHPDGHP HTXDo}HVOLQHDUHV e Q LQFyJQLWDV, P, Q, pode ser representado na IRUPDPDWULFLDO $ ; % onde, $ éa PDWUL]GRVFRHILFLHQWHV ; éa PDWUL]FROXQDGDVLQFyJQLWDV % éa PDWUL]FROXQDGRVWHUPRVLQGHSHQGHQWHV Note que, efectuando o produto das matrizes obtemos, e pela igualdade de matrizes recuperamos o sistema original.
12 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV12 Porque as operações HOHPHQWDUHVVREUHDVHTXDo}HV envolvem também os segundos membros, torna-se conveniente utilizar a chamada PDWUL]DPSOLDGD do sistema [ $ % ], Como por eemplo o sistema, tem como forma matricial $ ; % onde, e como matriz ampliada, Deste modo, as operações elementares podem ser aplicadas directamente às linhas da matriz ampliada, tal como no método de Gauss...
13 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV13 Å 2 PpWRGR GH HOLPLQDomR GH *DXVV Retomemos o sistema, [ [ [ [ [ [ [ [ cuja PDWUL]DPSOLDGD, [ $ % ]= Consideremos a sequência de RSHUDo}HVHOHPHQWDUHV efectuadas sobre as equações do sistema, mas vamos agora efectuá-las sobre as OLQKDVGDPDWUL]DPSOLDGD, / L com L { }. / ~ / / / ~ / / / ~ / ò/
14 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV14 Deste modo, obtivemos uma matriz ampliada que corresponde ao sistema, Este sistema é HTXLYDOHQWH ao inicial, mas possui uma propriedade muito conveniente: D PDWUL]GRVLVWHPDpWULDQJXODUVXSHULRU. Este facto permite-nos agora calcular a solução de forma simples, por sucessivas VXEVWLWXLo}HVDVFHQGHQWHV. Podemos então redefinir as RSHUDo}HVHOHPHQWDUHV, mas agora VREUHDV OLQKDVGDPDWUL]DPSOLDGD de um sistema linear. > 2SHUDo}HV HOHPHQWDUHV VREUH OLQKDV Representando as linhas da matriz ampliada por / L com L {P}. 7URFDUGXDVOLQKDV / L Ž / M 0XOWLSOLFDUXPDOLQKDSRUXPHVFDODUQmRQXOR / L ~D/ L com D $GLFLRQDUDXPDOLQKDRXWUDPXOWLSOLFDGDSRUXPHVFDODU / L ~ / L + E / M
15 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV15 Por eemplo o sistema, tem por PDWUL]DPSOLDGD, Efectuemos a sequência de RSHUDo}HVHOHPHQWDUHVVREUHOLQKDV: Trocar as duas primeiras linhas, / Ž / Somar à segunda, a primeira multiplicada por, Somar à terceira, a primeira multiplicada por ±, / ~ / / / ~ / ±/ Somar à terceira, a segunda multiplicada por, / ~ / /
16 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV16 Dividir a terceira por, / ~ / Donde, SRUVXEVWLWXLomRDVFHQGHQWH, obtemos o FRQMXQWRVROXomR O facto da matriz obtida ser WULDQJXODUVXSHULRU, tornou possível o cálculo da solução por VXEVWLWXLomRDVFHQGHQWH. Mas não é necessário tanto... Para que a substituição ascendente seja possível, basta que a matriz ampliada esteja HVFDORQDGDSRUOLQKDV. Diz-se que uma matriz está na IRUPDHVFDORQDGDSRUOLQKDV se satisfizer as seguintes condições: ƒ ƒ ƒ Se há linhas nulas elas situam-se abaio das linhas não nulas; O primeiro elemento não nulo de cada linha (com ecepção da primeira) situa-se à direita do primeiro elemento não nulo da linha anterior; Os elementos que se situam abaio do primeiro elemento não nulo de cada linha (com ecepção da última) são todos nulos. Aos primeiros elementos não nulos de cada linha chamam-se SLYRWV.
17 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV17 Por eemplo, estão HVFDORQDGDVSRUOLQKDV as matrizes, mas QmRHVWiescalonada por linhas a matriz, Diz-se que uma matriz está na IRUPDHVFDORQDGDUHGX]LGD se: estiver na forma escalonada por linhas e cada SLYRW é igual a e é o único elemento não nulo da sua coluna. Por eemplo, estão na IRUPDHVFDORQDGDUHGX]LGD as matrizes, Ou seja, os SLYRWV são todos iguais a e tanto abaio com acima deles todos os elementos são nulos.
18 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV18 Verifique que todas as matrizes seguintes estão HVFDORQDGDVSRUOLQKDV, mas apenas as matrizes de $ até $ estão na IRUPDUHGX]LGD. Note que, se para um dado sistema $; % conseguirmos obter a forma, ou seja, a matriz identidade, isso corresponde a um sistema na forma, com, $ ;, Q ; ; % e portanto está calculada a solução única do sistema, ; %. 7HRUHPD: Toda a matriz pode ser colocada na IRUPDHVFDORQDGD, mediante uma sequência finita de RSHUDo}HVHOHPHQWDUHV sobre as linhas. A GHPRQVWUDomR deste teorema é o próprio DOJRULWPRGH*DXVV.
19 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV19 2 PpWRGRGHHOLPLQDomRGH*DXVV SDUDFRQYHUWHUXPDPDWUL]jIRUPDHVFDORQDGDSRUOLQKDV Se todos os elementos da matriz forem nulos, parar. Procurar, da esquerda para a direita, a primeira coluna que tenha um elemento não nulo ( N) e mover essa linha para o topo da matriz. (RSFLRQDO) Multiplicar por N a primeira linha para que o primeiro SLYRW fique igual a. Anular cada elemento abaio do SLYRW, adicionando às linhas correspondentes múltiplos adequados da primeira linha. (DTXLDSULPHLUDOLQKDHDSULPHLUDFROXQDHVWmRMiFDOFXODGDV) Repetir de a para as restantes linhas. Para obter a IRUPDHVFDORQDGDUHGX]LGD de uma matriz aplica-se o PpWRGRGH HOLPLQDomRGH*DXVV-RUGDQ. 2 PpWRGRGHHOLPLQDomRGH*DXVV±-RUGDQ SDUDFRQYHUWHUXPDPDWUL]jIRUPDHVFDORQDGDUHGX]LGD Aplicar o método de eliminação de Gauss até produzir a forma escalonada por linhas. Transformar todos os pivots em. Aplicar o método de eliminação de Gauss de baio para cima por forma a anular todos os elementos da matriz situados acima e na mesma coluna dos pivots. Para isso, bastará começar na última linha não nula e, de baio para cima, adicionar a cada linha múltiplos adequados das linhas inferiores.
20 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV20 Por eemplo, consideremos o sistema que tem a PDWUL]DPSOLDGD, Começando pelo método de HOLPLQDomRGH*DXVV, A primeira linha cujo primeiro elemento é não nulo, é a terceira. Trocar com a primeira. Fazer o primeiro SLYRW. Anular todos os elementos abaio do SLYRW. DSULPHLUDOLQKDHDSULPHLUDFROXQDHVWmRFDOFXODGDV Repetir para as restantes linhas.
21 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV21 A primeira linha cujo primeiro elemento é não nulo, é a terceira. Trocar com a segunda. Fazer o segundo SLYRW. Anular todos os elementos abaio do SLYRW. DVHJXQGDOLQKDHDVHJXQGDFROXQDHVWmRWDPEpPFDOFXODGDV Repetir para as restantes linhas. Mas notamos que as duas linhas que restam são iguais. Eliminemos a última.
22 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV22 Fazer o terceiro SLYRW. E assim obtivemos a matriz na IRUPDHVFDORQDGDSRUOLQKDV. Note-se que esta matriz corresponde ao sistema, que pode facilmente ser FDOFXODGRSRUVXEVWLWXLomRDVFHQGHQWH. Mas vamos continuar, com método de HOLPLQDomRGH*DXVV-RUGDQ. Partindo da matriz escalonada por linhas, vamos anular os elementos acima dos SLYRWV, começando na primeira linha,
23 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV23 e anulando os restantes. E finalmente temos a matriz na IRUPDHVFDORQDGDUHGX]LGD. A matriz ampliada assim obtida corresponde ao sistema, HTXLYDOHQWH ao inicial, Trata-se obviamente de um VLVWHPDLQGHWHUPLQDGR, onde podemos eplicitar as três variáveis [, \ e ] em função de W. e apresentar o FRQMXQWRVROXomR na forma, onde W é a única YDULiYHOOLYUH.
24 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV24 Utilizando o PpWRGRGHHOLPLQDomRGH*DXVV-RUGDQ, mostre que o sistema, tem o FRQMXQWRVROXomR ^ ]±]] `. Utilizando o PpWRGRGHHOLPLQDomRGH*DXVV-RUGDQ, mostre que o sistema, é LPSRVVtYHO. Utilizando o PpWRGRGHHOLPLQDomRGH*DXVV-RUGDQ, mostre que o sistema, tem a VROXomR~QLFD ±.
25 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV25 Å 'LVFXVVmR GH 6LVWHPDV /LQHDUHV Comecemos por observar que, para uma dada matriz, a aplicação do método de Gauss (ou do método de Gauss-Jordan) conduz VHPSUH a uma matriz escalonada (ou escalonada reduzida) FRPRPHVPRQ~PHURGHSLYRWV. Recordemos o eemplo da página 20 onde, dada a matriz, obtivemos as formas: HVFDORQDGDSRUOLQKDV e HVFDORQDGDUHGX]LGD, ambas com SLYRWV. O mesmo teria acontecido para qualquer outra matriz escalonada, obtida a partir da inicial. Este eemplo trata da resolução de um sistema inicial de HTXDo}HV e LQFyJQLWDVque, como vimos, é SRVVtYHOHLQGHWHUPLQDGR, com JUDX GHLQGHWHUPLQDomR igual a. Essa ³LQGHWHUPLQDomR resultou precisamente do facto de ter ³GHVDSDUHFLGR uma equação e portanto também um SLYRW. E porque o ³SLYRWGHVDSDUHFLGR é o que corresponde à incógnitaw, apresentámos o FRQMXQWRVROXomR na forma, onde W éa YDULiYHOOLYUH.
26 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV26 Chamamos FDUDFWHUtVWLFDGHXPDPDWUL] $ ao número de pivots de uma qualquer PDWUL]HVFDORQDGD obtida de $ por aplicação sucessiva de operações elementares sobre as linhas de $. Representamos a característica de $ por U$ou FDU$. Sendo $ a matriz de um sistema, do tipo PlQ, então teremos sempre, U$d PLQ^PQ` Recordemos o segundo eemplo da página 24. Tratava-se da resolução de um sistema de HTXDo}HV e LQFyJQLWDV, com PDWUL]DPSOLDGD, donde se pode obter a forma HVFDORQDGDSRUOLQKDV, Neste caso, a matriz $ do sistema tem SLYRWV, mas a matriz ampliada [$ _%] tem SLYRWV. Como vimos, o VLVWHPDpLPSRVVtYHO e essa ³LPSRVVLELOLGDGH resulta precisamente do facto da terceira linha representar uma ³LJXDOGDGHLPSRVVtYHO
27 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV27 Por outro lado, o eemplo da página 15, de um sistema de HTXDo}HV e LQFyJQLWDV, conduziu à matriz ampliada HVFDORQDGDSRUOLQKDV, que tem SLYRWV e, como vimos, o sistema é SRVVtYHOHGHWHUPLQDGR. 'LVFXVVmRGHXPVLVWHPD Dado o sistema $; % onde $ é uma matriz do tipo PlQ % é uma matriz do tipo Pl Construir a matriz ampliada 0 [ $ % ] Aplicar o PpWRGRGH*DXVV ou o PpWRGRGH*DXVV-RUGDQ. D Se, durante a aplicação do método, surgir uma linha do tipo, _D com D œ 0, então o VLVWHPDpLPSRVVtYHO. Parar! E Senão, terminar o processo até obter uma matriz na forma HVFDORQDGD SRUOLQKDV ou HVFDORQDGDUHGX]LGD. Representemos esta matriz por 0. Nesta matriz, o Q~PHURGHFROXQDVVHPSLYRW corresponde ao Q~PHUR GH YDULiYHLVOLYUHV, ou JUDXGHLQGHWHUPLQDomR,
28 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV28 Para escolher as variáveis dependentes e as livres pode-se efectuar o seguinte raciocínio: YDULiYHLVOLYUHV FROXQDVVHPSLYRW YDULiYHLVGHSHQGHQWHV FROXQDVFRPSLYRW Se a matriz tiver pivots em todas as colunas correspondentes às LQFyJQLWDV, isto é, então não eistem variáveis livres e o sistema é SRVVtYHOHGHWHUPLQDGR. 7HRUHPD: Seja $ ; % um VLVWHPDGHHTXDo}HVOLQHDUHV, onde $ éuma matriz do tipo PlQ e % é uma matriz do tipo Pl. Eistem três possibilidades de classificação: 1. $ ; % é SRVVtYHOHGHWHUPLQDGR se e só se, U$ U[$_%] Q 2. $ ; % é SRVVtYHOHLQGHWHUPLQDGR se e só se, U$ U[$_%] < Q etem JUDXGHLQGHWHUPLQDomR Q ±U$ Q±U[$_%] 3. $ ; % é LPSRVVtYHO se e só se, U$œ U[$_%]
29 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV29 E sistematizando, LPSRVVtYHO U$œ U[$_%] SRVVtYHOHGHWHUPLQDGR U$ U[$_%] Q SRVVtYHO SRVVtYHOHLQGHWHUPLQDGR U$ U[$_%] < Q Por eemplo, procuremos uma UHODomR entre D e E para o seguinte VLVWHPD seja SRVVtYHO, Construindo a matriz ampliada e aplicando o método de eliminação de Gauss,
30 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV30 Para que o sistema seja SRVVtYHO é necessário e suficiente que, ou seja que, U$ U[$_%] E±D± E±D Caso contrário a última linha representaria uma ³LJXDOGDGHLPSRVVtYHO.
31 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV31 Considere o sistema linear, Determine os valores dos SDUkPHWURV D e E para os quais o sistema é, L LL LPSRVVtYHO SRVVtYHOHGHWHUPLQDGR 5HVROYDR, pelo método de eliminação de Gauss, para D e E. Construindo a matriz ampliada e aplicando o método de eliminação de Gauss,
32 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV32 obtemos a matriz escalonada, L O sistema será LPSRVVtYHOse e só se, U$œ U[$_%], ou seja, D ± e E œ D e E œ LL O sistema será SRVVtYHOHGHWHUPLQDGRse e só se, U$ U[$_%], ou seja, D±œ ¾ D œ 5HVROYHU, para D e E. Pelas alíneas anteriores, sabemos já que vai ser SRVVtYHOHLQGHWHUPLQDGR. Substituindo D e E na matriz escalonada já calculada,
33 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV33 Ou seja, obtivemos o VLVWHPD HTXLYDOHQWHDRLQLFLDO, E porque, na matriz escalonada a ³FROXQDVHPSLYRW corresponde à variável W, eplicitamos, e apresentamos o FRQMXQWRVROXomR na forma, 6ROXomR:
34 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV34 Å 6LVWHPD KRPRJpQHRV Num sistema KRPRJpQHR de equações lineares, WRGRVRVWHUPRV LQGHSHQGHQWHVVmRQXORV e tem portanto como representação matricial, $ ; pl1 ( ou simplesmente $; ) Então, todo o sistema homogéneo tem sempre SHORPHQRVXPDVROXomR, a solução nula, ; [ ] 7 por isso chamada a VROXomRWULYLDO do sistema homogéneo. Por eemplo o sistema, tem, como solução única, a VROXomRWULYLDO. Por outro lado o sistema, é um sistema homogéneo possível e indeterminado, cuja solução é o conjunto, { ±]]] } ao qual pertence a VROXomRWULYLDO. Naturalmente, isso acontece porque se trata de um sistema com LQFyJQLWDV e HTXDo}HV.
35 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV35 7HRUHPD: Se um sistema de equações lineares homogéneo tem PDLV LQFyJQLWDVTXHHTXDo}HV, então eiste uma VROXomRQmRWULYLDO. DePRQVWUDomR: Seja então $ ; pl1 onde $ é uma matriz do tipo SlT comt! S PDLVLQFyJQLWDVGRTXHHTXDo}HV Como um sistema homogéneo é VHPSUHSRVVtYHO, então, U$ U[$_]. Ecomo U$d PLQ^ST` então U$d S T Assim, U$< T FDUDFWHUtVWLFDLQIHULRUDRQ~PHURGHLQFyJQLWDV o sistema é LQGHWHUPLQDGR e tem portanto alguma VROXomRQmRWULYLDO. Os sistemas homogéneos possuem algumas propriedades muito simples, mas bastante úteis. 3URSULHGDGH: Se ; K é uma solução do sistema homogéneo $ ;, então D ; K também é solução, para qualquer D. 'HPRQVWUDomR: Se $; K então $D ; K D $; K D.
36 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV36 Por eemplo para o sistema, cuja solução é o conjunto, { ±]]] } Como ± é uma solução, obviamente que também o serão: ±, ±, ±,... 3URSULHGDGH: Se ; e ; são soluções do sistema homogéneo $ ;, então ; ; também é solução. 'HPRQVWUDomR: Se $; e $ ; então $; ; $; $;. Para o mesmo eemplo: Se ± e ± são soluções obviamente que também ± é solução. Deste modo, mostrámos também que TXDOTXHUFRPELQDomROLQHDUGH VROXo}HV de um sistema homogéneo é ainda solução.
37 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV37 Para qualquer sistema $ ; %, podemos considerar o VLVWHPDKRPRJpQHR DVVRFLDGR $ ;. Por eemplo para o sistema, o VLVWHPDKRPRJpQHRDVVRFLDGR é, Naturalmente a matriz $ é a mesma para ambos, mas as respectivas PDWUL]HV DPSOLDGDV serão [$_%] e [$_]. Aplicado o método de Gauss, obtemos as PDWUL]HVDPSOLDGDVHVFDORQDGDV. Neste caso, ambos os sistemas são SRVVtYHLVHGHWHUPLQDGRV, tendo o sistema completo a VROXomR~QLFD e o sistema homogéneo associado apenas a VROXomRWULYLDO. Assim, podemos apresentar a solução do sistema completo como a VRPDGDV VROXo}HV únicas dos dois sistemas, { }
38 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV38 Consideremos agora o seguinte sistema e respectivo VLVWHPDKRPRJpQHR DVVRFLDGR, Construídas as matrizes ampliadas e aplicado o método do Gauss obtemos: Para o VLVWHPDFRPSOHWR, o que significa que o sistema é SRVVtYHOHLQGHWHUPLQDGR e equivalente a, e tem por FRQMXQWRVROXomR, { ±]±]]] } Para o VLVWHPDKRPRJpQHRDVVRFLDGR, o que significa que o sistema homogéneo também é SRVVtYHOHLQGHWHUPLQDGR e equivalente a,
39 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV39 e que tem por FRQMXQWRVROXomR, { ]±]]] } Temos então, para o VLVWHPDFRPSOHWR a solução, { ±]±]]] } e para o VLVWHPDKRPRJpQHRDVVRFLDGR a solução, { ]±]]] } Se no FRQMXQWRVROXomRGRVLVWHPDFRPSOHWR escolhermos uma VROXomR SDUWLFXODU, por eemplo, aquela que corresponde a ], ou seja, ± então podemos apresentar a VROXomRJHUDOGRVLVWHPDFRPSOHWR, como a VRPDGHVWDVROXomRSDUWLFXODU, com a VROXomRJHUDOGRVLVWHPDKRPRJpQHRDVVRFLDGR: { ±]±]]] }
40 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV40 3URSRVLomR: Seja ; S uma solução particular do sistema de equações lineares $ ; %. Então, ; é solução do sistema VHHVyVH eiste uma solução ; K do sistema homogéneo associado, $ ; pl1, tal que ; ; S ; K. DePRQVWUDomR: Se ; S é uma VROXomR do sistema $; %, então $; S %. (Á) Se ; é WDPEpPVROXomR do sistema $ ; %, então $; %. E nesse caso, $; S $; $; S ± $; pl1 $; S ±; pl1 ou seja, ; K ; S ±; é WDPEpPVROXomR do sistema $; %. ( ) Se ; K éumavroxomr do sistema homogéneo associado, $ ; pl1, então $; K pl1. E nesse caso, $; $; S ; K $; S $; K %$; K % pl1 % e portanto ; é uma solução do sistema completo $ ; %.
41 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV41 ([HUFtFLRV: Resolva cada um dos sistemas seguintes e apresente a solução como a soma de uma solução particular com a solução geral do sistema homogéneo associado. 6ROXomR: { ±±]]]] } 6ROXomR: { ±}
x As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas.
 Å 6pULHV GH SRWrQFLDV As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas. Um eemplo típico é a série, O cálculo do valor
Å 6pULHV GH SRWrQFLDV As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas. Um eemplo típico é a série, O cálculo do valor
Notas sobre a Fórmula de Taylor e o estudo de extremos
 Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
4 Sistemas de Equações Lineares
 Nova School of Business and Economics Apontamentos Álgebra Linear 4 Sistemas de Equações Lineares 1 Definição Rank ou característica de uma matriz ( ) Número máximo de linhas de que formam um conjunto
Nova School of Business and Economics Apontamentos Álgebra Linear 4 Sistemas de Equações Lineares 1 Definição Rank ou característica de uma matriz ( ) Número máximo de linhas de que formam um conjunto
Exercícios 1. Determinar x de modo que a matriz
 setor 08 080509 080509-SP Aula 35 MATRIZ INVERSA Uma matriz quadrada A de ordem n diz-se invertível, ou não singular, se, e somente se, existir uma matriz que indicamos por A, tal que: A A = A A = I n
setor 08 080509 080509-SP Aula 35 MATRIZ INVERSA Uma matriz quadrada A de ordem n diz-se invertível, ou não singular, se, e somente se, existir uma matriz que indicamos por A, tal que: A A = A A = I n
Equações Diferenciais Ordinárias
 Equações Diferenciais Ordinárias Uma equação diferencial é uma equação que relaciona uma ou mais funções (desconhecidas com uma ou mais das suas derivadas. Eemplos: ( t dt ( t, u t d u ( cos( ( t d u +
Equações Diferenciais Ordinárias Uma equação diferencial é uma equação que relaciona uma ou mais funções (desconhecidas com uma ou mais das suas derivadas. Eemplos: ( t dt ( t, u t d u ( cos( ( t d u +
Capítulo 3 - Sistemas de Equações Lineares
 Capítulo 3 - Sistemas de Equações Lineares Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/
Capítulo 3 - Sistemas de Equações Lineares Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/
Introdução ao estudo de equações diferenciais
 Matemática (AP) - 2008/09 - Introdução ao estudo de equações diferenciais 77 Introdução ao estudo de equações diferenciais Introdução e de nição de equação diferencial Existe uma grande variedade de situações
Matemática (AP) - 2008/09 - Introdução ao estudo de equações diferenciais 77 Introdução ao estudo de equações diferenciais Introdução e de nição de equação diferencial Existe uma grande variedade de situações
Capítulo 3 - Sistemas de Equações Lineares
 Capítulo 3 - Sistemas de Equações Lineares Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/
Capítulo 3 - Sistemas de Equações Lineares Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/
INSTITUTO TECNOLÓGICO
 PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
Truques e Dicas. = 7 30 Para multiplicar fracções basta multiplicar os numeradores e os denominadores: 2 30 = 12 5
 Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
[a11 a12 a1n 4. SISTEMAS LINEARES 4.1. CONCEITO. Um sistema de equações lineares é um conjunto de equações do tipo
 4. SISTEMAS LINEARES 4.1. CONCEITO Um sistema de equações lineares é um conjunto de equações do tipo a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 11 x 1 + a 12 x 2 +... + a 1n x n = b 2... a n1 x 1 + a
4. SISTEMAS LINEARES 4.1. CONCEITO Um sistema de equações lineares é um conjunto de equações do tipo a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 11 x 1 + a 12 x 2 +... + a 1n x n = b 2... a n1 x 1 + a
Unidade II - Sistemas de Equações Lineares
 Unidade II - Sistemas de Equações Lineares 1- Situando a Temática Discutiremos agora um dos mais importantes temas da matemática: Sistemas de Equações Lineares Trata-se de um tema que tem aplicações dentro
Unidade II - Sistemas de Equações Lineares 1- Situando a Temática Discutiremos agora um dos mais importantes temas da matemática: Sistemas de Equações Lineares Trata-se de um tema que tem aplicações dentro
4. Tangentes e normais; orientabilidade
 4. TANGENTES E NORMAIS; ORIENTABILIDADE 91 4. Tangentes e normais; orientabilidade Uma maneira natural de estudar uma superfície S consiste em considerar curvas γ cujas imagens estão contidas em S. Se
4. TANGENTES E NORMAIS; ORIENTABILIDADE 91 4. Tangentes e normais; orientabilidade Uma maneira natural de estudar uma superfície S consiste em considerar curvas γ cujas imagens estão contidas em S. Se
Expansão linear e geradores
 Espaços Vectoriais - ALGA - 004/05 4 Expansão linear e geradores Se u ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u ; u ; :::;
Espaços Vectoriais - ALGA - 004/05 4 Expansão linear e geradores Se u ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u ; u ; :::;
Sistema de equações lineares
 Sistema de equações lineares Sistema de m equações lineares em n incógnitas sobre um corpo ( S) a x + a x + + a x = b a x + a x + + a x = b a x + a x + + a x = b 11 1 12 2 1n n 1 21 1 22 2 2n n 2 m1 1
Sistema de equações lineares Sistema de m equações lineares em n incógnitas sobre um corpo ( S) a x + a x + + a x = b a x + a x + + a x = b a x + a x + + a x = b 11 1 12 2 1n n 1 21 1 22 2 2n n 2 m1 1
Numa turma de 26 alunos, o número de raparigas excede em 4 o número de rapazes. Quantos rapazes há nesta turma?
 GUIÃO REVISÕES Equações e Inequações Equações Numa turma de 6 alunos, o número de raparigas ecede em 4 o número de rapazes. Quantos rapazes há nesta turma? O objectivo do problema é determinar o número
GUIÃO REVISÕES Equações e Inequações Equações Numa turma de 6 alunos, o número de raparigas ecede em 4 o número de rapazes. Quantos rapazes há nesta turma? O objectivo do problema é determinar o número
Distribuição de probabilidades
 Luiz Carlos Terra Para que você possa compreender a parte da estatística que trata de estimação de valores, é necessário que tenha uma boa noção sobre o conceito de distribuição de probabilidades e curva
Luiz Carlos Terra Para que você possa compreender a parte da estatística que trata de estimação de valores, é necessário que tenha uma boa noção sobre o conceito de distribuição de probabilidades e curva
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Um sistema de equações lineares (sistema linear) é um conjunto finito de equações lineares da forma:
 Sistemas Lineares Um sistema de equações lineares (sistema linear) é um conjunto finito de equações lineares da forma: s: 2 3 6 a) 5 2 3 7 b) 9 2 3 Resolução de sistemas lineares Metodo da adição 4 100
Sistemas Lineares Um sistema de equações lineares (sistema linear) é um conjunto finito de equações lineares da forma: s: 2 3 6 a) 5 2 3 7 b) 9 2 3 Resolução de sistemas lineares Metodo da adição 4 100
E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO
 E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO Dizemos que uma equação é linear, ou de primeiro grau, em certa incógnita, se o maior expoente desta variável for igual a um. Ela será quadrática, ou
E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO Dizemos que uma equação é linear, ou de primeiro grau, em certa incógnita, se o maior expoente desta variável for igual a um. Ela será quadrática, ou
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
MATEMÁTICA A - 12o Ano Probabilidades - Triângulo de Pascal Propostas de resolução
 MATEMÁTICA A - 12o Ano Probabilidades - Triângulo de Pascal Propostas de resolução Exercícios de exames e testes intermédios 1. A linha do triângulo de Pascal em que a soma dos dois primeiros elementos
MATEMÁTICA A - 12o Ano Probabilidades - Triângulo de Pascal Propostas de resolução Exercícios de exames e testes intermédios 1. A linha do triângulo de Pascal em que a soma dos dois primeiros elementos
Seu pé direito nas melhores faculdades
 Seu pé direito nas melhores faculdades IM - maio 006 MTMÁTI 0. a) atore a epressão 3 3 + 6. b) Resolva, em, a inequação 3 3 + 6 +. a) 3 3 + 6 = (3 ) 6(3 ) = ( 6)(3 ) = ( + 6 )( 6 )(3 ) é a forma fatorada
Seu pé direito nas melhores faculdades IM - maio 006 MTMÁTI 0. a) atore a epressão 3 3 + 6. b) Resolva, em, a inequação 3 3 + 6 +. a) 3 3 + 6 = (3 ) 6(3 ) = ( 6)(3 ) = ( + 6 )( 6 )(3 ) é a forma fatorada
Frações. Números Racionais
 Frações Números Racionais Consideremos a operação 4:5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números porque não há
Frações Números Racionais Consideremos a operação 4:5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números porque não há
INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU DEPARTAMENTO DE MATEMÁTICA
 INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU DEPARTAMENTO DE MATEMÁTICA Apontamentos: Curso de Conhecimentos Básicos de Matemática Cursos do Departamento de Gestão Maria Cristina
INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU DEPARTAMENTO DE MATEMÁTICA Apontamentos: Curso de Conhecimentos Básicos de Matemática Cursos do Departamento de Gestão Maria Cristina
Valores e Vectores Próprios. Carlos Luz Departamento de Matemática Escola Superior de Tecnologia de Setúbal
 Valores e Vectores Próprios Carlos Luz Departamento de Matemática Escola Superior de Tecnologia de Setúbal Ano Lectivo 24/25 Conteúdo Definição de Valor e Vector Próprios 2 2 Um Eemplo de Aplicação 8 3
Valores e Vectores Próprios Carlos Luz Departamento de Matemática Escola Superior de Tecnologia de Setúbal Ano Lectivo 24/25 Conteúdo Definição de Valor e Vector Próprios 2 2 Um Eemplo de Aplicação 8 3
MATEMÁTICA GEOMETRIA ANALÍTICA I PROF. Diomedes. E2) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B.
 I- CONCEITOS INICIAIS - Distância entre dois pontos na reta E) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B. d(a,b) = b a E: Dados os pontos A e B de coordenadas
I- CONCEITOS INICIAIS - Distância entre dois pontos na reta E) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B. d(a,b) = b a E: Dados os pontos A e B de coordenadas
Resolução de sistemas lineares
 Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA CURSO BIETÁPICO EM ENGENHARIA CIVIL º ciclo Regime Diurno/Nocturno Disciplina de COMPLEMENTOS DE MATEMÁTICA Ano lectivo de 7/8 - º Semestre Etremos
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA CURSO BIETÁPICO EM ENGENHARIA CIVIL º ciclo Regime Diurno/Nocturno Disciplina de COMPLEMENTOS DE MATEMÁTICA Ano lectivo de 7/8 - º Semestre Etremos
A Torre de Hanói e o Princípio da Indução Matemática
 A Torre de Hanói e o Princípio da Indução Matemática I. O jogo A Torre de Hanói consiste de uma base com três pinos e um certo número n de discos de diâmetros diferentes, colocados um sobre o outro em
A Torre de Hanói e o Princípio da Indução Matemática I. O jogo A Torre de Hanói consiste de uma base com três pinos e um certo número n de discos de diâmetros diferentes, colocados um sobre o outro em
A otimização é o processo de
 A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Eiste um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento de otimização.
A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Eiste um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento de otimização.
QUESTÕES COMENTADAS E RESOLVIDAS
 LENIMAR NUNES DE ANDRADE INTRODUÇÃO À ÁLGEBRA: QUESTÕES COMENTADAS E RESOLVIDAS 1 a edição ISBN 978-85-917238-0-5 João Pessoa Edição do Autor 2014 Prefácio Este texto foi elaborado para a disciplina Introdução
LENIMAR NUNES DE ANDRADE INTRODUÇÃO À ÁLGEBRA: QUESTÕES COMENTADAS E RESOLVIDAS 1 a edição ISBN 978-85-917238-0-5 João Pessoa Edição do Autor 2014 Prefácio Este texto foi elaborado para a disciplina Introdução
MD Sequências e Indução Matemática 1
 Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Sistemas Lineares. Módulo 3 Unidade 10. Para início de conversa... Matemática e suas Tecnologias Matemática
 Módulo 3 Unidade 10 Sistemas Lineares Para início de conversa... Diversos problemas interessantes em matemática são resolvidos utilizando sistemas lineares. A seguir, encontraremos exemplos de alguns desses
Módulo 3 Unidade 10 Sistemas Lineares Para início de conversa... Diversos problemas interessantes em matemática são resolvidos utilizando sistemas lineares. A seguir, encontraremos exemplos de alguns desses
ficha 3 espaços lineares
 Exercícios de Álgebra Linear ficha 3 espaços lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 3 Notação Sendo
Exercícios de Álgebra Linear ficha 3 espaços lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 3 Notação Sendo
Propriedades das Funções Deriváveis. Prof. Doherty Andrade
 Propriedades das Funções Deriváveis Prof Doerty Andrade 2005 Sumário Funções Deriváveis 2 Introdução 2 2 Propriedades 3 3 Teste da derivada segunda para máimos e mínimos 7 2 Formas indeterminadas 8 2 Introdução
Propriedades das Funções Deriváveis Prof Doerty Andrade 2005 Sumário Funções Deriváveis 2 Introdução 2 2 Propriedades 3 3 Teste da derivada segunda para máimos e mínimos 7 2 Formas indeterminadas 8 2 Introdução
4 Mudança de Coordenadas
 Material by: Caio Guimarães (Equipe Rumoaoita.com) Última atualização: 14 de outubro de 006 4 Mudança de Coordenadas Translação e Rotação de Curvas no R² Introdução O enfoque dos 3 primeiros capítulos
Material by: Caio Guimarães (Equipe Rumoaoita.com) Última atualização: 14 de outubro de 006 4 Mudança de Coordenadas Translação e Rotação de Curvas no R² Introdução O enfoque dos 3 primeiros capítulos
Eventos independentes
 Eventos independentes Adaptado do artigo de Flávio Wagner Rodrigues Neste artigo são discutidos alguns aspectos ligados à noção de independência de dois eventos na Teoria das Probabilidades. Os objetivos
Eventos independentes Adaptado do artigo de Flávio Wagner Rodrigues Neste artigo são discutidos alguns aspectos ligados à noção de independência de dois eventos na Teoria das Probabilidades. Os objetivos
a 1 x 1 +... + a n x n = b,
 Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
Análise de Regressão Linear Simples e Múltipla
 Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Carla Henriques (DepMAT ESTV) Análise de Regres. Linear Simples e Múltipla
Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Carla Henriques (DepMAT ESTV) Análise de Regres. Linear Simples e Múltipla
Lista 1 para a P2. Operações com subespaços
 Lista 1 para a P2 Observação 1: Estes exercícios são um complemento àqueles apresentados no livro. Eles foram elaborados com o objetivo de oferecer aos alunos exercícios de cunho mais teórico. Nós sugerimos
Lista 1 para a P2 Observação 1: Estes exercícios são um complemento àqueles apresentados no livro. Eles foram elaborados com o objetivo de oferecer aos alunos exercícios de cunho mais teórico. Nós sugerimos
Tabelas vista de estrutura
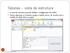 Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
Problemas de Valor Inicial para Equações Diferenciais Ordinárias
 Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
FACULDADE DE CIÊNCIA E TECNOLOGIA. Cursos de Engenharia. Prof. Álvaro Fernandes Serafim
 FACULDADE DE CIÊNCIA E TECNOLOGIA Cursos de Engenharia Prof. Álvaro Fernandes Serafim Última atualização: //7. Esta apostila de Álgebra Linear foi elaborada pela Professora Ilka Rebouças Freire. A formatação
FACULDADE DE CIÊNCIA E TECNOLOGIA Cursos de Engenharia Prof. Álvaro Fernandes Serafim Última atualização: //7. Esta apostila de Álgebra Linear foi elaborada pela Professora Ilka Rebouças Freire. A formatação
SOCIEDADE BRASILEIRA DE MATEMÁTICA MESTRADO PROFISSIONAL EM REDE NACIONAL PROFMAT
 SOCIEDADE BRASILEIRA DE MATEMÁTICA MESTRADO PROFISSIONAL EM REDE NACIONAL PROFMAT GABARITO da 3 a Avaliação Nacional de Aritmética - MA14-21/12/2013 Questão 1. (pontuação: 2) (1,0) a) Enuncie e demonstre
SOCIEDADE BRASILEIRA DE MATEMÁTICA MESTRADO PROFISSIONAL EM REDE NACIONAL PROFMAT GABARITO da 3 a Avaliação Nacional de Aritmética - MA14-21/12/2013 Questão 1. (pontuação: 2) (1,0) a) Enuncie e demonstre
AV1 - MA 12-2012. (b) Se o comprador preferir efetuar o pagamento à vista, qual deverá ser o valor desse pagamento único? 1 1, 02 1 1 0, 788 1 0, 980
 Questão 1. Uma venda imobiliária envolve o pagamento de 12 prestações mensais iguais a R$ 10.000,00, a primeira no ato da venda, acrescidas de uma parcela final de R$ 100.000,00, 12 meses após a venda.
Questão 1. Uma venda imobiliária envolve o pagamento de 12 prestações mensais iguais a R$ 10.000,00, a primeira no ato da venda, acrescidas de uma parcela final de R$ 100.000,00, 12 meses após a venda.
VALE PARA 1, PARA 2, PARA 3,... VALE SEMPRE?
 VALE PARA 1, PARA 2, PARA 3,.... VALE SEMPRE? Renate Watanabe As afirmações abaio, sobre números naturais, são verdadeiras para os números 1, 2, 3 e muitos outros. Perguntamos: elas são verdadeiras sempre?
VALE PARA 1, PARA 2, PARA 3,.... VALE SEMPRE? Renate Watanabe As afirmações abaio, sobre números naturais, são verdadeiras para os números 1, 2, 3 e muitos outros. Perguntamos: elas são verdadeiras sempre?
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 1 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 1 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
Aula 4 Estatística Conceitos básicos
 Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
Exercícios Adicionais
 Exercícios Adicionais Observação: Estes exercícios são um complemento àqueles apresentados no livro. Eles foram elaborados com o objetivo de oferecer aos alunos exercícios de cunho mais teórico. Nós recomendamos
Exercícios Adicionais Observação: Estes exercícios são um complemento àqueles apresentados no livro. Eles foram elaborados com o objetivo de oferecer aos alunos exercícios de cunho mais teórico. Nós recomendamos
Aula 4 Conceitos Básicos de Estatística. Aula 4 Conceitos básicos de estatística
 Aula 4 Conceitos Básicos de Estatística Aula 4 Conceitos básicos de estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa
Aula 4 Conceitos Básicos de Estatística Aula 4 Conceitos básicos de estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa
Problemas de Otimização. Problemas de Otimização. Solução: Exemplo 1: Determinação do Volume Máximo
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Eemplo 1: Determinação
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Eemplo 1: Determinação
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Matrizes; Matrizes Especiais; Operações com Matrizes; Operações Elementares
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Matrizes; Matrizes Especiais; Operações com Matrizes; Operações Elementares
CURSO ONLINE RACIOCÍNIO LÓGICO
 AULA QUINZE: Matrizes & Determinantes (Parte II) Olá, amigos! Pedimos desculpas por não ter sido possível apresentarmos esta aula na semana passada. Motivos de força maior nos impediram de fazê-lo, mas
AULA QUINZE: Matrizes & Determinantes (Parte II) Olá, amigos! Pedimos desculpas por não ter sido possível apresentarmos esta aula na semana passada. Motivos de força maior nos impediram de fazê-lo, mas
1. Criar uma nova apresentação
 MANUAL DO Baixa da Banheira, 2006 1. Criar uma nova apresentação Para iniciar uma sessão de trabalho no PowerPoint é necessário criar uma nova apresentação para depois trabalhar a mesma. Ao iniciar uma
MANUAL DO Baixa da Banheira, 2006 1. Criar uma nova apresentação Para iniciar uma sessão de trabalho no PowerPoint é necessário criar uma nova apresentação para depois trabalhar a mesma. Ao iniciar uma
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
Corpos. Um domínio de integridade finito é um corpo. Demonstração. Seja D um domínio de integridade com elemento identidade
 Corpos Definição Um corpo é um anel comutativo com elemento identidade em que todo o elemento não nulo é invertível. Muitas vezes é conveniente pensar em ab 1 como sendo a b, quando a e b são elementos
Corpos Definição Um corpo é um anel comutativo com elemento identidade em que todo o elemento não nulo é invertível. Muitas vezes é conveniente pensar em ab 1 como sendo a b, quando a e b são elementos
Introdução MATRIZES. O que vocês acham? Onde podemos usar Matrizes além dos estudos de matemática?
 PROBBILIDDES Professora Rosana Relva Números Inteiros e Racionais Introdução rrelva@globo.com O crescente uso dos computadores tem feito com que a teoria das matrizes seja cada vez mais aplicada. Onde
PROBBILIDDES Professora Rosana Relva Números Inteiros e Racionais Introdução rrelva@globo.com O crescente uso dos computadores tem feito com que a teoria das matrizes seja cada vez mais aplicada. Onde
por séries de potências
 Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Retas e Planos. Equação Paramétrica da Reta no Espaço
 Retas e lanos Equações de Retas Equação aramétrica da Reta no Espaço Considere o espaço ambiente como o espaço tridimensional Um vetor v = (a, b, c) determina uma direção no espaço Dado um ponto 0 = (x
Retas e lanos Equações de Retas Equação aramétrica da Reta no Espaço Considere o espaço ambiente como o espaço tridimensional Um vetor v = (a, b, c) determina uma direção no espaço Dado um ponto 0 = (x
C5. Formação e evolução estelar
 AST434: C5-1/68 AST434: Planetas e Estrelas C5. Formação e evolução estelar Mário João P. F. G. Monteiro Mestrado em Desenvolvimento Curricular pela Astronomia Mestrado em Física e Química em Contexto
AST434: C5-1/68 AST434: Planetas e Estrelas C5. Formação e evolução estelar Mário João P. F. G. Monteiro Mestrado em Desenvolvimento Curricular pela Astronomia Mestrado em Física e Química em Contexto
Faculdade Sagrada Família
 AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
Construção dos números racionais, Números fracionários e operações com frações
 Construção dos números racionais, Números fracionários e operações com frações O número racional pode ser definido a partir da aritmética fechamento da operação de divisão entre inteiros ou partir da geometria
Construção dos números racionais, Números fracionários e operações com frações O número racional pode ser definido a partir da aritmética fechamento da operação de divisão entre inteiros ou partir da geometria
Estudaremos métodos numéricos para resolução de sistemas lineares com n equações e n incógnitas. Estes podem ser:
 1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
Discussão de Sistemas Teorema de Rouché Capelli
 Material by: Caio Guimarães (Equipe Rumoaoita.com) Discussão de Sistemas Teorema de Rouché Capelli Introdução: Apresentamos esse artigo para mostrar como utilizar a técnica desenvolvida a partir do Teorema
Material by: Caio Guimarães (Equipe Rumoaoita.com) Discussão de Sistemas Teorema de Rouché Capelli Introdução: Apresentamos esse artigo para mostrar como utilizar a técnica desenvolvida a partir do Teorema
PROBABILIDADE Prof. Adriano Mendonça Souza, Dr.
 PROBABILIDADE Prof. Adriano Mendonça Souza, Dr. Departamento de Estatística - PPGEMQ / PPGEP - UFSM - O intelecto faz pouco na estrada que leva à descoberta, acontece um salto na consciência, chameo de
PROBABILIDADE Prof. Adriano Mendonça Souza, Dr. Departamento de Estatística - PPGEMQ / PPGEP - UFSM - O intelecto faz pouco na estrada que leva à descoberta, acontece um salto na consciência, chameo de
Raciocínio Lógico para o INSS Resolução de questões Prof. Adeilson de melo REVISÃO 01 - conjuntos e porcentagens
 APRESENTAÇÃO Olá, prezados concursandos! Sejam bem-vindos à resolução de questões de Raciocínio Lógico preparatório para o INSS. Mais uma vez, agradeço ao convite do prof. Francisco Júnior pela oportunidade
APRESENTAÇÃO Olá, prezados concursandos! Sejam bem-vindos à resolução de questões de Raciocínio Lógico preparatório para o INSS. Mais uma vez, agradeço ao convite do prof. Francisco Júnior pela oportunidade
Roteiro de Estudos do 1ª Trimestre 2ªSérie Disciplina: Matemática Professor: Hugo P.
 Roteiro de Estudos do 1ª Trimestre ªSérie Disciplina: Matemática Professor: Hugo P. Conteúdos para Avaliação Trimestral: Matrizes o Definição; lei de formação de uma Matriz; o Operações com matrizes (soma,
Roteiro de Estudos do 1ª Trimestre ªSérie Disciplina: Matemática Professor: Hugo P. Conteúdos para Avaliação Trimestral: Matrizes o Definição; lei de formação de uma Matriz; o Operações com matrizes (soma,
Universidade Federal do Rio Grande do Norte. Centro De Ciências Exatas e da Terra. Departamento de Física Teórica e Experimental
 Universidade Federal do Rio Grande do Norte Centro De Ciências Exatas e da Terra Departamento de Física Teórica e Experimental Programa de Educação Tutorial Curso de Nivelamento: Pré-Cálculo PET DE FÍSICA:
Universidade Federal do Rio Grande do Norte Centro De Ciências Exatas e da Terra Departamento de Física Teórica e Experimental Programa de Educação Tutorial Curso de Nivelamento: Pré-Cálculo PET DE FÍSICA:
Como enviar e receber correio eletrónico utilizando o Gmail
 Como enviar e receber correio eletrónico utilizando o Gmail Este módulo pressupõe que que já tenha criado uma conta de correio eletrónico no Gmail (caso já não se recorde como deve fazer, consulte o nosso
Como enviar e receber correio eletrónico utilizando o Gmail Este módulo pressupõe que que já tenha criado uma conta de correio eletrónico no Gmail (caso já não se recorde como deve fazer, consulte o nosso
ponto P terá as projecções P 1 e P 2. E o eixo X passa para X. Vamos ver o que acontece no plano do
 Mudança de planos 1- Introdução As projecções de uma figura só representam as suas verdadeiras grandezas se essa figura está contida num plano paralelo aos planos de projecção. Caso contrário as projecções
Mudança de planos 1- Introdução As projecções de uma figura só representam as suas verdadeiras grandezas se essa figura está contida num plano paralelo aos planos de projecção. Caso contrário as projecções
O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2
 3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
4Distribuição de. freqüência
 4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
Canguru Matema tico sem Fronteiras 2013
 Canguru Matema tico sem Fronteiras 201 http://www.mat.uc.pt/canguru/ Destinata rios: alunos dos 12. ano de escolaridade Durac a o: 1h 0min Turma: Nome: Na o podes usar calculadora. Em cada questa o deves
Canguru Matema tico sem Fronteiras 201 http://www.mat.uc.pt/canguru/ Destinata rios: alunos dos 12. ano de escolaridade Durac a o: 1h 0min Turma: Nome: Na o podes usar calculadora. Em cada questa o deves
7 - Análise de redes Pesquisa Operacional CAPÍTULO 7 ANÁLISE DE REDES. 4 c. Figura 7.1 - Exemplo de um grafo linear.
 CAPÍTULO 7 7 ANÁLISE DE REDES 7.1 Conceitos Básicos em Teoria dos Grafos Diversos problemas de programação linear, inclusive os problemas de transporte, podem ser modelados como problemas de fluxo de redes.
CAPÍTULO 7 7 ANÁLISE DE REDES 7.1 Conceitos Básicos em Teoria dos Grafos Diversos problemas de programação linear, inclusive os problemas de transporte, podem ser modelados como problemas de fluxo de redes.
CAPÍTULO 2. Grafos e Redes
 CAPÍTULO 2 1. Introdução Um grafo é uma representação visual de um determinado conjunto de dados e da ligação existente entre alguns dos elementos desse conjunto. Desta forma, em muitos dos problemas que
CAPÍTULO 2 1. Introdução Um grafo é uma representação visual de um determinado conjunto de dados e da ligação existente entre alguns dos elementos desse conjunto. Desta forma, em muitos dos problemas que
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/59 2 - FUNDAMENTOS 2.1) Teoria dos Conjuntos 2.2) Números
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/59 2 - FUNDAMENTOS 2.1) Teoria dos Conjuntos 2.2) Números
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias
 Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
Álgebra Linear Resumo das aulas teóricas e práticas Paulo R. Pinto http://www.math.ist.utl.pt/ ppinto/ Lisboa, Novembro de 2011
 Álgebra Linear Resumo das aulas teóricas e práticas Paulo R Pinto http://wwwmathistutlpt/ ppinto/ Lisboa, Novembro de 2011 Conteúdo 1 Matrizes e sistemas lineares 1 11 Álgebra das Matrizes 1 12 Operações
Álgebra Linear Resumo das aulas teóricas e práticas Paulo R Pinto http://wwwmathistutlpt/ ppinto/ Lisboa, Novembro de 2011 Conteúdo 1 Matrizes e sistemas lineares 1 11 Álgebra das Matrizes 1 12 Operações
Análise de Arredondamento em Ponto Flutuante
 Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica
 O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
1 Propagação de Onda Livre ao Longo de um Guia de Ondas Estreito.
 1 I-projeto do campus Programa Sobre Mecânica dos Fluidos Módulos Sobre Ondas em Fluidos T. R. Akylas & C. C. Mei CAPÍTULO SEIS ONDAS DISPERSIVAS FORÇADAS AO LONGO DE UM CANAL ESTREITO As ondas de gravidade
1 I-projeto do campus Programa Sobre Mecânica dos Fluidos Módulos Sobre Ondas em Fluidos T. R. Akylas & C. C. Mei CAPÍTULO SEIS ONDAS DISPERSIVAS FORÇADAS AO LONGO DE UM CANAL ESTREITO As ondas de gravidade
N1Q1 Solução. a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas.
 1 N1Q1 Solução a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas. b) Há várias formas de se cobrir o tabuleiro com peças dos tipos A e B, com pelo
1 N1Q1 Solução a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas. b) Há várias formas de se cobrir o tabuleiro com peças dos tipos A e B, com pelo
Manual do Gestor da Informação do Sistema
 Faculdade de Engenharia da Universidade do Porto Licenciatura Informática e Computação Laboratório de Informática Avançada Automatização de Horários Manual do Gestor da Informação do Sistema João Braga
Faculdade de Engenharia da Universidade do Porto Licenciatura Informática e Computação Laboratório de Informática Avançada Automatização de Horários Manual do Gestor da Informação do Sistema João Braga
Conceitos Fundamentais
 Capítulo 1 Conceitos Fundamentais Objetivos: No final do Capítulo o aluno deve saber: 1. distinguir o uso de vetores na Física e na Matemática; 2. resolver sistema lineares pelo método de Gauss-Jordan;
Capítulo 1 Conceitos Fundamentais Objetivos: No final do Capítulo o aluno deve saber: 1. distinguir o uso de vetores na Física e na Matemática; 2. resolver sistema lineares pelo método de Gauss-Jordan;
x As IyUPXODVGHGLIHUHQFLDomRQXPpULFD podem ser obtidas por: x
 &DStWXOR±'LIHUHQFLDomRH,QWHJUDomR1XPpULFDV > 'LIHUHQFLDomR 1XPpULFD Por vezes é necessário obterydoruhvgdvghulydgdvde uma função VHP UHFRUUHUjUHVSHFWLYDH[SUHVVmRDQDOtWLFD, por esta não ser conhecida ou
&DStWXOR±'LIHUHQFLDomRH,QWHJUDomR1XPpULFDV > 'LIHUHQFLDomR 1XPpULFD Por vezes é necessário obterydoruhvgdvghulydgdvde uma função VHP UHFRUUHUjUHVSHFWLYDH[SUHVVmRDQDOtWLFD, por esta não ser conhecida ou
MÉDIA ARITMÉTICA MÉDIA PONDERADA MODA MEDIANA
 MÉDIA ARITMÉTICA MÉDIA PONDERADA MODA MEDIANA Em um amostra, quando se têm os valores de uma certa característica, é fácil constatar que os dados normalmente não se distribuem uniformemente, havendo uma
MÉDIA ARITMÉTICA MÉDIA PONDERADA MODA MEDIANA Em um amostra, quando se têm os valores de uma certa característica, é fácil constatar que os dados normalmente não se distribuem uniformemente, havendo uma
Pedro Ribeiro 2014/2015
 Programação Dinâmica Pedro Ribeiro DCC/FCUP 2014/2015 Pedro Ribeiro (DCC/FCUP) Programação Dinâmica 2014/2015 1 / 56 Números de Fibonacci Sequência de números muito famosa definida por Leonardo Fibonacci
Programação Dinâmica Pedro Ribeiro DCC/FCUP 2014/2015 Pedro Ribeiro (DCC/FCUP) Programação Dinâmica 2014/2015 1 / 56 Números de Fibonacci Sequência de números muito famosa definida por Leonardo Fibonacci
Matemática. Euclides Roxo. David Hilbert. George F. B. Riemann. George Boole. Niels Henrik Abel. Karl Friedrich Gauss.
 Matemática Jacob Palis Álgebra 1 Euclides Roxo David Hilbert George F. B. Riemann George Boole Niels Henrik Abel Karl Friedrich Gauss René Descartes Gottfried Wilhelm von Leibniz Nicolaus Bernoulli II
Matemática Jacob Palis Álgebra 1 Euclides Roxo David Hilbert George F. B. Riemann George Boole Niels Henrik Abel Karl Friedrich Gauss René Descartes Gottfried Wilhelm von Leibniz Nicolaus Bernoulli II
Preparação para o teste intermédio de Matemática 8º ano
 Preparação para o teste intermédio de Matemática 8º ano Conteúdos do 7º ano Conteúdos do 8º ano Conteúdos do 8º Ano Teorema de Pitágoras Funções Semelhança de triângulos Ainda os números Lugares geométricos
Preparação para o teste intermédio de Matemática 8º ano Conteúdos do 7º ano Conteúdos do 8º ano Conteúdos do 8º Ano Teorema de Pitágoras Funções Semelhança de triângulos Ainda os números Lugares geométricos
Operações com números racionais decimais
 Divisão 1º: Divisão exata Operações com números racionais decimais Considere a seguinte divisão: 1,4 : 0,05 Transformando em frações decimais, temos: Método prático 1º) Igualamos o números de casas decimais,
Divisão 1º: Divisão exata Operações com números racionais decimais Considere a seguinte divisão: 1,4 : 0,05 Transformando em frações decimais, temos: Método prático 1º) Igualamos o números de casas decimais,
Facturação Guia do Utilizador
 Facturação Guia do Utilizador Facturação Como se utiliza 2 1 Como se utiliza Todas as opções do sistema estão acessíveis através do menu: ou do menu: O Menu caracteriza-se pelas seguintes funcionalidades:
Facturação Guia do Utilizador Facturação Como se utiliza 2 1 Como se utiliza Todas as opções do sistema estão acessíveis através do menu: ou do menu: O Menu caracteriza-se pelas seguintes funcionalidades:
Sumário - Introdução
 Introdução - O planeamento económico é um tipo de política estrutural Segundo Amaral é uma forma intervencionista de realizar política económica estrutural e baseia-se na preparação e execução de planos,
Introdução - O planeamento económico é um tipo de política estrutural Segundo Amaral é uma forma intervencionista de realizar política económica estrutural e baseia-se na preparação e execução de planos,
CAPÍTULO 6 TRANSFORMAÇÃO LINEAR
 INODUÇÃO AO ESUDO DA ÁLGEBA LINEA CAPÍULO 6 ANSFOMAÇÃO LINEA Introdução Muitos problemas de Matemática Aplicada envolvem o estudo de transformações, ou seja, a maneira como certos dados de entrada são
INODUÇÃO AO ESUDO DA ÁLGEBA LINEA CAPÍULO 6 ANSFOMAÇÃO LINEA Introdução Muitos problemas de Matemática Aplicada envolvem o estudo de transformações, ou seja, a maneira como certos dados de entrada são
Introdução ao MATLAB
 Introdução ao MATLAB O MATLAB é um programa cálculo numérico que pode ser usado interactivamente. A sua estrutura de dados fundamental é a matriz, que pode ter elementos reais ou complexos. Embora na sua
Introdução ao MATLAB O MATLAB é um programa cálculo numérico que pode ser usado interactivamente. A sua estrutura de dados fundamental é a matriz, que pode ter elementos reais ou complexos. Embora na sua
Álgebra Linear. Mauri C. Nascimento Departamento de Matemática UNESP/Bauru. 19 de fevereiro de 2013
 Álgebra Linear Mauri C. Nascimento Departamento de Matemática UNESP/Bauru 19 de fevereiro de 2013 Sumário 1 Matrizes e Determinantes 3 1.1 Matrizes............................................ 3 1.2 Determinante
Álgebra Linear Mauri C. Nascimento Departamento de Matemática UNESP/Bauru 19 de fevereiro de 2013 Sumário 1 Matrizes e Determinantes 3 1.1 Matrizes............................................ 3 1.2 Determinante
Só Matemática O seu portal matemático http://www.somatematica.com.br FUNÇÕES
 FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
