UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil

Transcrição

1 UNIVERSIDADE ESTADUAL AULISTA UNES - Camus de Bauru/S FACULDADE DE ENGENHARIA Deartamento de Engenharia Civil Discilina: CONCRETO ROTENDIDO NOTAS DE AULA CONCRETO ROTENDIDO rof. Dr. AULO SÉRGIO DOS SANTOS BASTOS ( Bauru/S Maio/2015

2 ARESENTAÇÃO Esta aostila tem o objetivo de servir como notas de aula na discilina Concreto rotendido, do curso de Engenharia Civil da Faculdade de Engenharia, da Universidade Estadual aulista UNES, Camus de Bauru/S. O texto aresentado está de acordo com as rescrições contidas na norma NBR 6118/2014 ( rojeto de estruturas de concreto rocedimento ), ara o rojeto e dimensionamento de elementos em Concreto Armado e rotendido. A aostila aresenta o estudo inicial de temas de Concreto rotendido. A bibliografia indicada deve ser consultada ara arofundar o arendizado, bem como os textos aresentados na ágina da discilina na internet: htt:// O autor agradece a Tiago Duarte de Mattos, ela confecção dos desenhos. Críticas e sugestões serão bem-vindas.

3 SUMÁRIO 1. ROTENSÃO NAS ESTRUTURAS DE CONCRETO EXEMLOS DE ESTRUTURAS ROTENDIDAS CONCRETO ROTENDIDO X CONCRETO ARMADO EXEMLO BREVE HISTÓRICO DO CONCRETO ROTENDIDO FABRICAÇÃO DE EÇAS ROTENDIDAS ARMADURA DE ROTENSÃO RÉ-TRACIONADA ARMADURA DE ROTENSÃO ÓS-TRACIONADA MATERIAIS CONCRETO AÇO DE ARMADURA ATIVA Aresentação Quanto ao tratamento Normas brasileiras Exemlos de designação Massa Esecífica, Coeficiente de Dilatação Térmica e Módulo de Elasticidade Acondicionamento Diagrama tensão-deformação BAINHAS CALDA DE CIMENTO ANCORAGENS VALORES-LIMITES DE TENSÃO OR OCASIÃO DA OERAÇÃO DE ROTENSÃO NA ARMADURA VALORES RERESENTATIVOS DA FORÇA DE ROTENSÃO FORÇA DE ROTENSÃO i NA ARMADURA FORÇA DE ROTENSÃO a FORÇA DE ROTENSÃO o NA ARMADURA/CONCRETO FORÇA DE ROTENSÃO t NA ARMADURA/CONCRETO ERDAS DE ROTENSÃO ESCORREGAMENTO DOS FIOS NA ANCORAGEM EM ISTA DE ROTENSÃO RELAXAÇÃO INICIAL DA ARMADURA NA RÉ-TRAÇÃO RETRAÇÃO INICIAL DO CONCRETO EM ISTA DE ROTENSÃO VARIAÇÃO DA FORÇA DE ROTENSÃO DE i A a DETERMINAÇÃO DA FORÇA o NA RÉ-TRAÇÃO DETERMINAÇÃO DE o NA ÓS-TRAÇÃO ERDA OR ATRITO NA ÓS-TRAÇÃO ERDAS NA ANCORAGEM NA ÓS-TRAÇÃO ERDA DE ROTENSÃO NA ÓS-TRAÇÃO OR DEFORMAÇÃO IMEDIATA DO CONCRETO ELO ESTIRAMENTO DOS CABOS RESTANTES RETRAÇÃO E FLUÊNCIA INICIAL DO CONCRETO NA ÓS-TRAÇÃO DETERMINAÇÃO DA FORÇA DE ROTENSÃO FINAL ERDA DE ROTENSÃO OR RETRAÇÃO DO CONCRETO VALOR DA RETRAÇÃO... 45

4 9.14 ERDA DE ROTENSÃO OR FLUÊNCIA DO CONCRETO Anexo A Fluência do Concreto (A.2.2) ERDAS ROGRESSIVAS rocesso Simlificado ara o Caso de Fases Únicas de Oeração (Item ) rocesso Aroximado do Item Método Geral de Cálculo CRITÉRIOS DE ROJETO Estado-Limite Último (ELU) Estado-Limite de Serviço (ELS) AÇÕES A CONSIDERAR NOS ESTADOS-LIMITES DE SERVIÇO COMBINAÇÕES DE SERVIÇO NÍVEIS DE ROTENSÃO ESTIMATIVA DA FORÇA DE ROTENSÃO rotensão Comleta rotensão Limitada rotensão arcial DETERMINAÇÃO DA FORÇA i VERIFICAÇÃO DE TENSÕES NORMAIS NA SEÇÃO DE CONCRETO MAIS SOLICITADA ELO CARREGAMENTO EXTERNO VERIFICAÇÃO DE TENSÕES NORMAIS AO LONGO DO VÃO ROCESSO DAS CURVAS LIMITES Limitações de Tensões ara o Estado em Vazio Limitações de Tensões ara o Estado em Serviço Curvas Limites ara as Tensões Devidas à rotensão Exemlo de Curvas Limites ROCESSO DO FUSO LIMITE Estado em Vazio Estado em Serviço Traçado do Fuso Limite ANÁLISE DA RESISTÊNCIA ÚLTIMA À FLEXÃO (ELU) TIOS DE RUTURA OR FLEXÃO RÉ-ALONGAMENTO DETERMINAÇÃO DO MOMENTO FLETOR ÚLTIMO Seção Retangular SEÇÃO T ROTEIRO ARA CÁLCULO DE M u EXEMLOS DE CÁLCULO DE M ud ANÁLISE DO ESTADO-LIMITE ÚLTIMO RELATIVO À FORÇA CORTANTE EFEITOS DA FORÇA CORTANTE EFEITO DA COMONENTE TANGENCIAL DA FORÇA DE ROTENSÃO VERIFICAÇÃO DO ESTADO-LIMITE ÚLTIMO (ELU) Modelo de Cálculo I Modelo de Cálculo II QUESTIONÁRIO BIBLIOGRAFIA... 94

5 1 1. ROTENSÃO NAS ESTRUTURAS DE CONCRETO O concreto é um material resistente às tensões de comressão, mas sua resistência à tração varia de 8 a 15 % da resistência à comressão. Sob flexão, o concreto desenvolve fissuras, ainda em estágios iniciais de carregamento, e ara reduzir ou imedir tais fissuras, uma força de comressão concêntrica ou excêntrica ode ser imosta na direção longitudinal do elemento, que age eliminando ou reduzindo as tensões de tração nas seções críticas do meio do vão e dos aoios, elevando a caacidade das seções à flexão, à força cortante e à torção. As seções odem atuar elasticamente e a caacidade total do concreto à comressão ode ser eficientemente utilizada, em toda a altura da seção, a todas as ações alicadas. Estudo comlementar: ler Hanai (2002), item 1.2 A rotensão alicada ao concreto,.3 a 11. Definição: uma eça é considerada de Concreto rotendido quando é submetida à ação de forças eseciais e ermanentemente alicadas, chamadas forças de rotensão, e quando a eça é submetida à ação simultânea dessas forças, das cargas ermanentes e variáveis, o concreto não seja solicitado à tração ou só o seja dentro dos limites ermitidos. Exemlo (Figura 1), onde M é o momento fletor solicitante e a força de rotensão: M M+ A Viga t, c,m c, + t,m 0 c - Figura 1 Tensões normais numa viga rotendida. Na fibra inferior de uma viga rotendida, sob momento fletor ositivo, ode resultar tensão nula, tensão de comressão ou de tração. Atividade comlementar: ler em Hanai (2002): Os dez mandamentos do engenheiro de C..,.i, ii, e o item 1.1 O que se entende or rotensão? (.1 a 3). 2. EXEMLOS DE ESTRUTURAS ROTENDIDAS Na Figura 2 até a Figura 7 são mostrados exemlos de estruturas em Concreto rotendido.

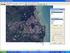
6 UNES (Bauru/S) 2139 Concreto rotendido Figura 2 onte em Concreto rotendido (C) em Vitória/ES. Figura 3 Laje alveolar ré-moldada em C. Figura 4 avimento de edifício em laje nervurada rotendida. 2

7 UNES (Bauru/S) 2139 Concreto rotendido 3 Figura 5 - avimentos de edifício em laje maciça rotendida. Figura 6 Lajes ré-moldadas rotendidas. Figura 7 Seção dulo T em Concreto rotendido ré-moldado. 3. CONCRETO ROTENDIDO X CONCRETO ARMADO 1. Concreto rotendido utiliza concretos e aços de alta resistência (aços até 2100 Ma e concretos até 85 Ma); 2. Em Concreto rotendido toda a seção transversal resiste às tensões; 3. Devido aos itens 1 e 2, elementos de Concreto rotendido são mais leves, mais esbeltos e esteticamente mais bonitos; 4. Concreto rotendido fica livre de fissuras, com todas as vantagens daí rovenientes; 5. Concreto rotendido aresenta melhor controle de flechas;

8 4 6. Concreto rotendido tem melhor resistência às forças cortantes (devido à inclinação dos cabos róximos aos aoios e a ré-comressão que reduz as tensões de tração diagonais); 7. O aço é ré-testado durante o estiramento. Estudo comlementar: Concreto rotendido, catálogo da emresa Rudloff. 3.1 EXEMLO Laje simlesmente aoiada, h 30,5 cm, d d s 25,4 cm, f cd 34,5 Ma, f,ef Ma, f yd 435 Ma, f c,máx 13,8 Ma (tensão máxima à comressão ermitida no concreto), L 9,14 m, γ concr 16,76 kn/m 3 (concreto leve), q 5,11 kn/m 2 (ação variável). A laje será calculada tomando-se uma faixa igual à sua altura (b 30,5 cm - Figura 8), ao invés de um metro, de modo que as quantidades de armadura que serão calculadas são relativas à largura b da faixa. d s 25,4 30,5 30,5cm Figura 8 Dimensões (cm) da seção transversal da laje. Momento fletor da carga ermanente (M g ) na faixa b 30,5 cm: g 16,76. 0,305. 0,305 1,56 kn/m M 2 g 1,56.9,14 16,28 kn.m kn.cm 8 Tensões normais no too e na base da seção (não fissurada): 6Mg ± ± ± 0,345 kn/cm 2 ± 3,45 Ma 2 2 bh 30,5. 30,5 Momento fletor da carga variável (M q ) na faixa b 30,5 cm: q 5,11. 0,305 1,56 kn/m M M kn.cm q g São aresentados a seguir diversos casos ossíveis ara o dimensionamento da laje. 1) Laje não-armada A tensão final máxima de 6,9 Ma, de comressão na borda suerior e de tração na borda inferior, é menor que a tensão máxima de comressão ermitida (f c,máx 13,8 Ma), orém, é maior que a resistência à tração na flexão máxima do concreto (módulo de rutura), o que faz a laje fissurar e romer.

9 5 3,45-3,45-6,9 - Μ g + Μ q + 3,45 + 3,45 + 6,9 Figura 9 Tensões normais (Ma) nas bordas da laje sem armaduras, devidas aos carregamentos ermanente e variável. 2) Laje em Concreto Armado (ELU) cd 0,85f cd x 0,8x R cc LN d - 0,4x sd R st Figura 10 Laje em Concreto Armado no Estado Limite Último (ELU). M d 1,4 (M g + M q ) M d 1,4 ( ) kn.cm M d 0,68b w x f cd (d 0,4x) ,68. 30,5. x. 3,45 (25,4 0,4x) x 2 63,5x + 159,25 0 x 2,62 cm dom. 2 (x 2lim 0,26d 0,26. 25,4 6,6 cm) A s Md sd ( d 0,4x) 43, ( 25,4 0,4. 2,62) 4,30 cm 2 3) Laje em Concreto rotendido: rotensão axial Assumindo que nenhuma tensão de tração é ermitida.

10 6 CG ( Μ g ) ( Μ q ) 3,45 3, () 6,9 13,8 Μ g Μ q ,45 + 3,45 6,9 0 Figura 11 Tensões normais (Ma) na laje com rotensão axial. ara resultar tensão final nula na face inferior da laje é necessário imor uma tensão de comressão, roorcionada or uma força de rotensão, de tal modo que: (base) g (base) + q (base) 3,45 + 3,45 6,9 Ma Força de rotensão:. A c ( 0,69) 30,5. 30,5 641,9 kn 64 tf Área da armadura de rotensão: A 641,9 5,81 cm 2 f 110,4,ef A força de rotensão () aumentou a tensão de comressão na borda suerior ara 13,8 Ma, igual à tensão máxima ermitida (f c,máx 13,8 Ma). Uma osição mais conveniente ara a força de rotensão ode diminuir esta tensão resultante. 4) Laje em Concreto rotendido: rotensão excêntrica Assumindo a força de rotensão no limite do núcleo central de inércia (h/6 ara seção retangular). Considerando que a tensão na face inferior da laje deve ser nula, a força de rotensão deverá causar uma tensão de comressão de 6,9 Ma na face inferior. A força de rotensão, ortanto, deve ser: ( ) A 2 base c 0,69. 30,5 320,9 kn 2 2 Área da armadura de rotensão: A 320,9 2,91cm 2 f 110,4,ef

11 7 h 6 30,5 6 5,08 cm ( Μ g + Μ q ) 6,9 - () 0 6,9 + Μ g + Μ q ,9 6,9 0 Figura 12 Tensões normais (Ma) na laje com rotensão excêntrica, com osicionada no limite do núcleo central de inércia. A armadura de rotensão é metade da armadura do caso anterior. O resultado mostra a grande imortância da osição de alicação da força de rotensão. A força de rotensão excêntrica diminuiu a tensão final na borda suerior ara 6,9 Ma, menor que f c,máx. 5) Laje em Concreto rotendido: máxima excentricidade da força de rotensão A tensão na base devida à força de rotensão excêntrica é:. e ( ) 6e + base Ac bh Ac h 6 5,09 e máx 10,16 cm ( Μ g + Μ q ) 6,9 - () 2,3 + 4,6 Μ g + Μ q ,9-6,9 0 Figura 13 Tensões normais (Ma) na laje com excentricidade máxima da força de rotensão.

12 8 Assumindo e e máx 10,16 cm e (base) 6,9 Ma (ara resultar tensão nula na base da laje), a força de rotensão será: 6.10,16 0, ,1 kn 2 30,5 30, 5 Área da armadura de rotensão: A 214,1 1,94 cm 2 f 110,4,ef A força de rotensão com a máxima excentricidade causa tensão de tração na borda suerior, combatida ela tensão de comressão da carga ermanente. A maior excentricidade da força de rotensão diminuiu a tensão final de comressão no too da laje, comarando-se com os casos anteriores. Tensão normal na borda suerior devida à força de rotensão: 214,1 6.10,16 (too) 1 0,23 2 kn/cm 2 2,3 Ma (tensão de tração) 30,5 30,5 6) Laje em Concreto rotendido: tração igual à máxima ermitida Assumindo que uma tensão normal de tração de 1,46 Ma seja ermitida na borda inferior da laje, sob a carga de serviço, a força de rotensão assa a ser: 6.10, ,5 30, 5 ( 0,69 + 0,146 ) 1 + Área de armadura de rotensão: A 168,8 1,53 cm 2 f 110,4,ef 168,8 kn A Tabela 1 aresenta um resumo dos resultados numéricos, obtidos ara os casos analisados. Tabela 1 Resumo dos resultados numéricos. Soluções / Laje c,máx t,máx (Ma) (Ma) (kn) A s ou A (cm 2 ) Não-armada (*) 6,9 6,9 - - Concreto Armado ,30 C.. rotensão axial 13, ,9 5,81 C.. no limite do núcleo central 6, ,9 2,91 C.. c/ excentricidade máxima 4, ,1 1,94 C.. tração na borda 5,1 1,46 168,8 1,53 * a laje romeu. Nota: ler exemlo numérico em Hanai (2002),.11 a 17.

13 9 4. BREVE HISTÓRICO DO CONCRETO ROTENDIDO No mundo: rimeira alicação de rotensão nos Estados Unidos, or H. Jackson; atente ara lajes rotendidas or Doehring Alemanha; Wettstein Alemanha fabricou aineis rotendidos; Freyssinet França aresentou o rimeiro trabalho consistente sobre Concreto rotendido. Inventou métodos construtivos, equiamentos, aços e concretos eseciais; rimeira conferência, na França. Walder construiu a rimeira onte em balanços sucessivos norma alemã DIN No Brasil: a rimeira onte em C.. no Rio de Janeiro, com sistema Freyssinet; Comanhia Belgo-Mineira iniciou a fabricação de aço de rotensão. 5. FABRICAÇÃO DE EÇAS ROTENDIDAS Aresentam-se a seguir as formas de fabricação de eças rotendidas, considerando eças com ré-tração e com ós-tração. 5.1 ARMADURA DE ROTENSÃO RÉ-TRACIONADA É aquele em que o estiramento da armadura de rotensão é feito utilizando-se aoios indeendentes da eça, antes do lançamento do concreto, sendo desfeita a vinculação da armadura com os aoios aós ocorrido o endurecimento do concreto. A transferência da força de rotensão da armadura ara a eça ocorre devido à aderência entre o concreto e a armadura, sendo este sistema também chamado concreto rotendido com aderência inicial. eças de Concreto rotendido ré-tracionadas são geralmente fabricadas em istas de rotensão, ara ossibilitar a moldagem de um grande número de eças simultaneamente, geralmente idênticas. A cura úmida a vaor é comum, a fim de ermitir a transferência da força de rotensão em até 24 horas. Devido à baixa idade do concreto, encurtamentos elásticos e deformação lenta tendem a atingir valores altos, com consequente redução do alongamento da armadura de rotensão, ou seja, ocorre uma relativamente alta erda de rotensão. Cilindro hidráulico ("macaco") Cabo Fôrma da eça Ancoragem assiva ista de rotenção Bloco de reação Figura 14 Esquema simlificado de ista de rotensão, ara fabricação de eças rotendidas com ré-tração.

14 10 Na Figura 15 até a Figura 19 são ilustradas fábricas com istas de rotensão. Figura 15 ista de rotensão em fábrica de laje alveolar. Figura 16 - ista de rotensão em fábrica de laje ré-moldada. Figura 17 - ista de rotensão em fábrica de laje ré-moldada.

15 11 Figura 18 - ista de rotensão em fábrica de dormente ferroviário de concreto. Figura 19 - ista de rotensão em fábrica de dormente ferroviário de concreto. 5.2 ARMADURA DE ROTENSÃO ÓS-TRACIONADA As eças fabricadas com ós-tração odem ter aderência entre a armadura de rotensão e o concreto da eça, bem como odem também serem fabricadas sem a aderência. No concreto rotendido ós-tracionado, o estiramento da armadura de rotensão é realizado aós o endurecimento do concreto, utilizando-se, como aoios, artes da rória eça, criando-se osteriormente aderência com o concreto de modo ermanente.

16 12 a) eça concretada duto vazado b) Estiramento da armadura de rotenção A c) Armadura ancorada e dutos reenchidos com nata de cimento A Figura 20 Esquema simlificado de fabricação de eça rotendida com ós-tração. Neste caso, o duto é reenchido com nata de cimento, de modo a criar aderência entre a armadura e o concreto, melhorando o controle da fissuração e a resistência última. Na Figura 21 até a Figura 23 são ilustradas a ós-tração. Figura 21 Moldagem da eça com bainha metálica (Catálogo Rudloff).

17 13 Figura 22 Oeração de estiramento da armadura de rotensão, aós o concreto da eça já aresentar a resistência à comressão necessária (Catálogo Rudloff). Figura 23 reenchimento da bainha com nata de cimento ara criar aderência entre a armadura e o concreto da eça (Catálogo Rudloff). É aquele obtido como no caso anterior, mas sem se criar a aderência da armadura de rotensão com o concreto. Geralmente usa-se a cordoalha engraxada como armadura de rotensão. Estudo comlementar: Ler Hanai,.17 a 20 e fazer o item 1.6; Ler catálogo Concreto rotendido da emresa Rudloff. 6. MATERIAIS O Concreto rotendido é comosto elos materiais concreto simles, aço de rotensão (armadura ativa) e geralmente contém também armadura assiva (CA-25, 50 ou 60). odem ocorrer também outros materiais, como disositivos de ancoragem, bainhas metálicas, etc.

18 CONCRETO A construção de estruturas de Concreto rotendido exige um controle de qualidade mais rigoroso do concreto. A resistência característica à comressão do concreto (f ck ) situa-se frequentemente na faixa entre 30 e 50 Ma, o que resulta estruturas com menor eso rório e maiores vãos. No caso de eças rotendidas ré-fabricadas são muitas vezes utilizados concretos de resistência suerior a 50 Ma. Concretos com resistências elevadas são desejáveis orque: a) as solicitações révias causadas ela força de rotensão odem ser muito elevadas; b) ermitem a redução das dimensões das eças, diminuindo o eso rório, imortante nos grandes vãos e eças ré-moldadas; c) ossuem maiores módulos de elasticidade (E c ), o que diminui as deformações imediatas, a deformação lenta e a retração, ou seja, as flechas e as erdas de rotensão são menores; d) geralmente são mais imermeáveis, o que é imortante ara diminuir a ossibilidade de corrosão da armadura de rotensão, que, or estar sob tensões muito elevadas, são mais suscetíveis à corrosão. A alicação do cimento C V ARI é muito comum, orque ossibilita a alicação da força de rotensão num temo menor, no caso da ós-tensão. Esecialmente nas eças de Concreto rotendido, a cura do concreto deve ser cuidadosa, a fim de ossibilitar a sua melhor qualidade ossível. A cura térmica a vaor é frequente na fabricação das eças ré-fabricadas, ara a rodução de maior quantidade de eças. Exemlo: com cimento ARI e cura a vaor consegue-se, em 12 h, cerca de 70 % da resistência à comressão aos 28 dias de cura normal. No rojeto das estruturas de Concreto rotendido, os seguintes arâmetros são imortantes, e devem ser esecificadas elo rojetista: a) resistências características à comressão (f ckj ) e à tração (f ctkj ), na idade j da alicação da rotensão e na idade de 28 dias; b) módulo de elasticidade do concreto na idade t o (E ci(to) ), quando se alica uma ação ermanente imortante, como a força de rotensão, bem como também aos 28 dias de idade; c) relação a/c do concreto. 6.2 AÇO DE ARMADURA ATIVA Caracterizam-se ela elevada resistência e or não ossuírem atamar de escoamento. A elevada resistência é exigida ara ermitir grandes alongamentos em regime elástico e ara comensar as erdas de rotensão, que odem alcançar 415 Ma. Deve aresentar também: ductilidade antes da rutura, boas roriedades de aderência, baixa relaxação e boa resistência à fadiga e à corrosão Aresentação a) fios trefilados de aço, diâmetro de 3 a 8 mm, em rolos ou bobinas; b) cordoalhas (fios enrolados em hélice, com 2, 3 ou 7 fios); c) barras de aço-liga de alta resistência, laminadas a quente, com φ 12 mm, e com comrimento limitado.

19 UNES (Bauru/S) 2139 Concreto rotendido 15 Figura 24 Cordoalha de sete fios engraxada e não engraxada (Catálogo ArcelorMittal). Figura 25 Barra de aço Dywidag, com disositivo de fixação (Catálogo Dywidag) Quanto ao tratamento a) aços de relaxação normal (RN); b) aços de relaxação baixa (RB): são aqueles que tem suas características elásticas melhoradas ara reduzir as erdas de tensão or relaxação, que é cerca de 25 % da relaxação do aço RN. Relaxação: é a erda de tensão com o temo em um aço estirado, sob comrimento e temeratura constantes. Quanto maior a tensão ou a temeratura, maior a relaxação do aço Normas brasileiras a) NBR 7482/08: Fios de aço ara Concreto rotendido - Esecificação ; b) NBR 7483/08: Cordoalhas de aço ara Concreto rotendido - Esecificação ; c) NBR 7484/09: Barras, cordoalhas e fios de aço destinados a armaduras de rotensão Método de ensaio de relaxação isotérmica ; d) NBR 6349/08: Barras, cordoalhas e fios de aço ara armaduras de rotensão Ensaio de tração Exemlos de designação a) C 175 RN: aço ara Concreto rotendido, com resistência característica mínima à tração (ftk) de 175 kn/cm2 (1.750 Ma) e de relaxação normal; b) C 190 RB: aço ara Concreto rotendido, com resistência característica mínima à tração (ftk) de 190 kn/cm2 (1.900 Ma) e de relaxação baixa.

20 16 Tabela 2 Esecificação de fios (Catálogo ArcelorMittal). Tabela 3 Esecificação de cordoalhas (Catálogo ArcelorMittal). Tabela 4 Esecificação de barra Dywidag St 85/105 (Catálogo ArcelorMittal).

21 Massa Esecífica, Coeficiente de Dilatação Térmica e Módulo de Elasticidade A NBR 6118 adota a massa esecífica de kg/m 3, e o coeficiente de dilatação térmica de 10-5 / C, ara intervalos de temeratura entre - 20 C e 100 C. ara o módulo de elasticidade a norma ermite adotar 200 Ga ( Ma kn/cm 2 ) ara fios e cordoalhas, quando o valor não for obtido em ensaio ou não for fornecido elo fabricante do aço. No item a norma aresenta características de ductilidade do aço e no aresenta a resistência à fadiga Acondicionamento Tabela 5 Dados do acondicionamento dos fios (Catálogo ArcelorMittal). Figura 26 Rolo de fio. Tabela 6 Dados do acondicionamento das cordoalhas (Catálogo ArcelorMittal).

22 18 Figura 27 Rolos de cordoalhas engraxada e não engraxada (Catálogo ArcelorMittal). Figura 28 - Rolos de fio e cordoalha (Catálogo ArcelorMittal) Diagrama tensão-deformação A NBR 6118 (item 8.4.5) esecifica que o diagrama tensão-deformação deve ser fornecido elo fabricante ou obtido em ensaio realizado segundo a NBR Na falta deles a NBR 6118 ermite, nos estados-limite de serviço e último, utilizar um diagrama simlificado, ara intervalos de temeraturas entre - 20 C e 150 C.

23 19 UNES (Bauru/S) 2139 Concreto rotendido ftk f yk f td f yd α yk yd uk Figura 29 Diagrama tensão-deformação simlificado indicado ela NBR 6118 ara aços de rotensão. tg α E módulo de elasticidade 200 Ga ara fios e cordoalhas (na falta de dados do fabricante e de ensaio); fyk resistência característica de escoamento convencional, corresondente à deformação residual de 0,2 %. Os valores característicos da resistência ao escoamento convencional fyk, da resistência à tração ftk e o alongamento aós rutura uk das cordoalhas devem satisfazer os valores mínimos estabelecidos na ABNT NBR Os valores de fyk, ftk e do alongamento aós rutura uk dos fios devem atender ao que é esecificado na ABNT NBR BAINHAS São tubos dentro dos quais a armadura de rotensão é colocada, utilizados em rotensão com aderência osterior ou também sem aderência. São fabricados em aço, com esessura de 0,1 a 0,35 mm, costurados em hélice. ara criar aderência com a armadura de rotensão, as bainhas são reenchidas com calda de cimento. Figura 30 Bainha metálica.

24 20 Figura 31 Bainha metálica. 6.4 CALDA DE CIMENTO A calda, ou nata de cimento injetada no interior da bainha metálica, tem como função roorcionar a aderência entre a armadura de rotensão e o concreto da eça, na ós-tração, e roteger a armadura contra a corrosão. Utiliza-se cerca de 36 a 44 kg de água ara cada 100 kg de cimento. A norma NBR 7681 ( Calda de cimento ara injeção ) fixa as condições exigidas ara as caldas. Figura 32 Equiamentos ara injeção de calda de cimento.

25 ANCORAGENS A forma mais simles e econômica de fixação dos fios e cordoalhas é or meio de cunhas e orta-cunhas. As cunhas odem ser bi ou triartidas, e ficam alojadas em cavidades de blocos ou lacas de aço (orta-cunha). No caso de armaduras ós-tracionadas, existem conjuntos de elementos, que constituem os chamados sistemas de rotensão, como Freyssinet, Dywidag, VSL, BBRV, Rudloff, Tensacciai, etc. Na Figura 32 até a Figura 49 ilustram-se vários tios de disositivos de ancoragem. Figura 33 Cunhas embutidas em ortas-cunha ara fixação de fios de rotensão. Figura 34 Disositivo de ancoragem.

26 22 Figura 35 - Disositivo de ancoragem. Figura 36 - Disositivo de ancoragem ara cordoalha engraxada. Figura 37 Disositivos ara ancoragem de cordoalha engraxada.

27 UNES (Bauru/S) 2139 Concreto rotendido Figura 38 - Ancoragem ativa de cordoalha engraxada. Figura 39 - Ancoragem assiva de cordoalha engraxada. Figura 40 - Ancoragem de cordoalha engraxada. 23

28 UNES (Bauru/S) 2139 Concreto rotendido Figura 41 Oeração de estiramento de cordoalha engraxada. Figura 42 Cilindros hidráulicos ara estiramento de cordoalha. Figura 43 Disositivo ara ancoragem ativa (Catálogo Rudloff). 24

29 25 Figura 44 - Disositivo ara ancoragem ativa (Catálogo Rudloff). Figura 45 - Disositivo ara ancoragem assiva (Catálogo Rudloff).

30 26 Figura 46 - Disositivo ara ancoragem assiva (Catálogo Rudloff). Figura 47 - Disositivo ara ancoragem assiva (Catálogo Rudloff).

31 27 Figura 48 - Disositivo ara emenda de armadura (Catálogo Rudloff). Figura 49 - Disositivo ara ancoragem de barras (Catálogo Dywidag). 7. VALORES-LIMITES DE TENSÃO OR OCASIÃO DA OERAÇÃO DE ROTENSÃO NA ARMADURA (NBR 6118, item ) A tensão na armadura de rotensão deve ser verificada ara diversas situações em serviço, a fim de evitar solicitações exageradas e deformações irreversíveis. Durante as oerações de rotensão, a tensão de tração na armadura não deve suerar os seguintes valores-limites: a) armadura ré-tracionada or ocasião da alicação da força de estiramento ( i ), a tensão i na armadura de rotensão na saída do aarelho de tração (cilindro hidráulico), deve reseitar os limites:

32 28 i i 0,77f 0,90f 0,77f 0,85f tk yk tk yk - ara aços RN - ara aços RB b) armadura ós-tracionada i i i 0,74f 0,87f 0,74f 0,82f 0,80f 0,88f tk yk tk yk tk yk - ara aços RN - ara aços RB - ara cordoalhas engraxadas RB i 0,72f 0,88f tk yk - ara aços C 85/105 em barras Ao término da oeração de rotensão, a tensão o(x) da armadura ré ou ós-tracionada, decorrente da força o(x), não deve suerar os limites do item b. 8. VALORES RERESENTATIVOS DA FORÇA DE ROTENSÃO Servem de orientação na verificação de esforços solicitantes e nas fases de execução da rotensão na obra ou na fábrica. As Figuras 50 e 51 ilustram os valores reresentativos da força de rotensão, em função do temo, ara os casos de eças rotendidas ré-tracionadas e ós-tracionadas.

33 8 UNES (Bauru/S) 2139 Concreto rotendido 29 i a ré-tração anc erda or escorregamento dos fios e acomodação da ancoragem r1 + cs1 { r1 erda or relaxação inicial da armadura r1 erda or retração inicial do concreto o e erda or deformação inicial do concreto r2 + cs2 + cc{ r2 erda or relaxação osterior da armadura cs2 erda or retração osterior do concreto cc erda or fluência osterior do concreto Estiramento da armadura início da retração do concreto alicação da rotenção ao concreto t t (temo) t - 2 t - 1 t 0 Figura 50 Diagrama força de rotensão x temo ara eça rotendida ré-tracionada. i ós-tração atr + anc { atr erda or atrito ao longo da armadura erda or escorregamento dos fios na anc ancoragem e acomodação da ancoragem 0 e erda or deformação imediata do concreto elo estiramento dos cabos restantes Estiramento do 1º cabo 8 0 e + cs1 + cc1 r1 t r2 + cs2 + cc2 8 r1 erda or relaxação inicial da armadura { cs1 erda or retração inicial do concreto cc1 erda or fluência inicial do concreto r2 erda or relaxação osterior da armadura { cs2 erda or retração osterior do concreto cc2 erda or fluência osterior do concreto t (temo) t 0 estiramento dos cabos restantes Figura 51 Diagrama força de rotensão x temo ara eça rotendida ós-tracionada.

34 30 Se os cabos (conjunto de fios ou cordoalhas ara formar uma armadura de rotensão) não forem retos, deve-se acrescentar a erda or atrito que ocorre nos desvios, à anc (erda de força de rotensão na ancoragem). 8.1 FORÇA DE ROTENSÃO i NA ARMADURA i força máxima alicada à armadura de rotensão elo equiamento de tração. É a força de rotensão alicada elos cilindros ( macacos ) hidráulicos na ista de rotensão, antes de ser realizada a ancoragem dos fios na cabeceira da ista, no bloco de ancoragem. No caso de ós-tração, é a força máxima alicada elos macacos hidráulicos antes da ancoragem com as cunhas. 8.2 FORÇA DE ROTENSÃO a Esta força de rotensão é considerada aenas no caso da ré-tração. a força na armadura de rotensão no instante imediatamente anterior à sua liberação das ancoragens externas. É a força i (força no macaco hidráulico) subtraídas as erdas de rotensão decorrentes do escorregamento dos fios (ou cordoalhas) e acomodação das ancoragens rovisórias nos blocos de ancoragem, da relaxação do aço e da retração inicial do concreto. Também ode-se dizer que é a força ancorada imediatamente anterior à transferência da força de rotensão ara o concreto. 8.3 FORÇA DE ROTENSÃO o NA ARMADURA/CONCRETO o(x) força de rotensão no temo t 0 na seção de abcissa x. É o valor inicial da força de rotensão transferida ao concreto (t 0). Na ré-tração é a força ancorada ( a ) diminuída da erda de rotensão or deformação imediata, devido ao encurtamento elástico do concreto. Na ós-tração é a força no macaco ( i ) diminuída das erdas de rotensão devidas ao atrito dos cabos nas bainhas, ao escorregamento dos fios (ou cordoalhas) na ancoragem e acomodação da ancoragem, da deformação imediata do concreto devida aos cabos restantes, da retração e fluência inicial do concreto e da relaxação inicial da armadura de rotensão. Este valor corresonde ao valor da força de rotensão antes das erdas rogressivas (decorrentes do temo) e acontece no instante imediatamente osterior à transferência da rotensão ao concreto. 8.4 FORÇA DE ROTENSÃO t NA ARMADURA/CONCRETO t(x) força de rotensão no temo t na seção de abcissa x. t(x) o(x) t(x) i o(x) t(x) o(x) força de rotensão na eça antes da ocorrência das erdas rogressivas; t(x) erdas de rotensão rogressivas (retração e fluência osterior do concreto e relaxação osterior da armadura). Ocorrem aós a alicação de o.

35 31 t é variável no temo t em função das erdas rogressivas, e tendem ao valor final da força de rotensão ( (x) ). força de rotensão final aós ocorridas todas as erdas. 9. ERDAS DE ROTENSÃO São aresentadas a seguir as metodologias alicadas no cálculo das diversas erdas de rotensão. 9.1 ESCORREGAMENTO DOS FIOS NA ANCORAGEM EM ISTA DE ROTENSÃO Ocorre devido ao escorregamento dos fios e acomodação das cunhas nos furos ortascunha, da ordem de 4 a 6 mm, deendendo do tio de armadura de rotensão e da existência ou não de istão de cravação de cunhas nos macacos de rotensão. O escorregamento causa erda aenas na ancoragem ativa; na ancoragem assiva a acomodação/escorregamento vai sendo anulada na oeração de estiramento. O valor da erda de rotensão or escorregamento/acomodação deende em grande arte do comrimento da ista de rotensão. Exemlo: - comrimento da ista 120 m mm; - deformação do aço 0,7 % 0,007; - alongamento do aço , mm 84 cm; - escorregamento/acomodação 6 mm; 6 anc 100 0,7 % 840 que ode ser considerado desrezível, orque a ista tem grande comrimento. Se a ista tivesse 25 m a erda de rotensão seria de 3,4 %, que já não é desrezível. 9.2 RELAXAÇÃO INICIAL DA ARMADURA NA RÉ-TRAÇÃO Relaxação é a erda de tensão com o temo em um aço estirado, sob comrimento e temeratura constantes. ara tensões alicadas até 0,5f tk, a erda or relaxação é desrezível, mas aumenta raidamente com maiores tensões e temeraturas. A relaxação ocorre a artir do instante que o aço é estirado. A erda de rotensão or relaxação inicial da armadura é aquela que ocorre no intervalo de temo entre o estiramento da armadura e a alicação da rotensão no concreto. A relaxação ocorre semre, mas ara cálculo de a considera-se aenas uma fração inicial. Conforme a NBR 6118 (item ), a intensidade da relaxação do aço deve ser determinada elo coeficiente ψ (t,t o ), calculado or: ψ ( t;t ) o r ( t; ) r t o ( t;t ) i o erda de tensão or relaxação ura desde o instante t o do estiramento da armadura até o instante t considerado; i tensão na armadura de rotensão no instante de seu estiramento.

36 32 As normas NBR 7482 e 7483 estabelecem valores médios ara o coeficiente de relaxação de fios e cordoalhas, medidos aós horas à temeratura constante de 20 C (ψ 1000 ), ara tensões variando de 0,5 e 0,8f tk. ara efeito de rojeto, os valores de ψ 1000 da Tabela 7 odem ser adotados. Tabela 7 - Valores de ψ 1000 (%), (NBR 6118, item 8.4.8). Cordoalhas Fios o RN RB RN RB Barras 0,5 f tk ,6 f tk 3,5 1,3 2,5 1,0 1,5 0,7 f tk 7,0 2,5 5,0 2,0 4,0 0,8 f tk 12,0 3,5 8,5 3,0 7,0 Obs.: interolar ara valores intermediários. RN é relaxação normal e RB é relaxação baixa. ara tensões inferiores a 0,5 f tk, admite-se que não haja erda de tensão or relaxação. ara o temo infinito ode-se considerar: Exemlo: ψ (t ;t o ) 2,5 ψ 1000 ara valores diferentes de horas, semre a 20 C, as exressões são: 0,15 t t o ψ ( t;t o ) ψ1000 (t em horas) ,15 t t o ψ ( t;t o ) ψ1000 (t em dias) 41,67 - temo curto: entre o estiramento e a alicação da rotensão no concreto 15 horas; - cordoalha RN e i 0,80 f tk - da Tabela 7: ψ ,0 % 0, ψ ( t;t o ) 12 6, 4 % 1000 erda or relaxação: r 6,4 100 ( t;t o ) ψ( t;t o ) i ( 0,80f tk ) 0,0512f tk A erda neste caso não é desrezível, e se utilizada cura a vaor, com elevação da temeratura na armadura de rotensão, a erda é ainda maior. 9.3 RETRAÇÃO INICIAL DO CONCRETO EM ISTA DE ROTENSÃO A retração inicial do concreto leva a uma erda de tensão na armadura. No ambiente de fábrica (ambiente úmido), com cura iniciada logo aós o adensamento, ode-se desrezar o efeito da retração inicial do concreto, mesmo orque o intervalo de temo entre a concretagem e a transferência da rotensão é equeno.

37 VARIAÇÃO DA FORÇA DE ROTENSÃO DE i A a Considerando cabos retos, ista longa e cura acelerada, uma estimativa é: 7 % aço RN + + i a anc r1 cs1 3 % aço RB 9.5 DETERMINAÇÃO DA FORÇA o NA RÉ-TRAÇÃO o força de rotensão corresondente ao instante imediatamente osterior à transferência da rotensão à eça. ré-tração: o a - e a força ancorada; e erda da força de rotensão devida à deformação imediata do concreto (encurtamento elástico). NBR 6118 (item ): A variação da força de rotensão em elementos estruturais com ré-tração, or ocasião da alicação da rotensão ao concreto, e em razão do seu encurtamento, deve ser calculada em regime elástico, considerando-se a deformação da seção homogeneizada. O módulo de elasticidade do concreto a considerar é o corresondente à data de rotensão, corrigido, se houver cura térmica. a a A c l Figura 52 Encurtamento elástico or deformação imediata do concreto, rotensão axial. c tensão no concreto ao nível da armadura de rotensão. Imediatamente aós a transferência da rotensão ara a eça, a mudança na deformação da armadura de rotensão ( ), causada elo encurtamento elástico do concreto, é igual à deformação do concreto ( c ) ao nível da armadura de rotensão, sendo a equação de comatibilidade exressa or: c e alicando a Lei de Hooke: E e E c c

38 34 A erda de rotensão é: e E E c c α c α E E c razão modular. c A a ch A ch área da seção homogeneizada: A c A c b. h A A c α. A h A ch A c + A c A b. h + (α 1) A b or simlicidade, em seções onde a quantidade de aço não é alta, faz-se A ch A c. Aós o encurtamento elástico, a força de rotensão na armadura será: a o a e a α A A ch Se a rotensão for excêntrica e atuar o eso rório da eça, fica: a e CG a ( ) a ( ) a ( ) M a A ch aih.e ² M Ih e Figura 53 Tensões normais na seção transversal, sob rotensão excêntrica e com atuação do eso rório. I h momento de inércia da seção homogeneizada. Tensão no concreto ao nível da armadura de rotensão:

39 35 c A a ch a e I h 2 M + I h e A exressão de c é válida quando se ode considerar a rotensão alicada numa única fibra. Quando a rotensão ocorrer em fibras distintas, como no caso de cordoalhas em vários níveis, a influência de uma sobre a outra deve ser avaliada, conforme rocesso aresentado em Hanai (2002). erda de rotensão: e α c o o A o a e Exemlo Calcule a erda de tensão na armadura de rotensão na seção 1-1, de uma viga rétensionada, assumindo que, antes da transferência da rotensão, a força ancorada era corresondente à tensão de 0,75f tk. A viga tem os seguintes dados: vão l 15,2 m ; eso rório (g ) 7,22 kn/m concreto C40 ; f ck(i) 30 Ma E ci α 5600 f, com α E 1,0 (brita de granito ou gnaisse) E E ci 1, Ma ck Armadura de rotensão (A ): 10 cordoalhas C 190 RB 12,7 (φ 12,7 mm), A 10. 0,988 9,88 cm 2 f tk Ma ; E 196 kn/mm Ma l 2 l 2 1 a e a 76 cm 1 l 15,2 m 10 cm 38 A Figura 54 Esquema da viga. Resolução

40 36 E Razão modular: α 6, 39 E ci A c cm I cm 4 12 or simlicidade: A ch A c e I h I Excentricidade da armadura de rotensão: 76 e cm 2 Força de rotensão ancorada ( a ): a 0,75f tk. A 0, , kn Momento fletor devido ao eso rório: M 2 7,22.15,2 208,51 kn.m kn.cm 8 A tensão no concreto, na fibra relativa ao CG da armadura de rotensão, no instante da transferência da força de rotensão é: a e M a e c + + 0, 860 Ach Ih Ih A erda de tensão or encurtamento elástico é: e c kn/cm 2 α 6,39 ( 0,860) 5,495 kn/cm 2 54,95 Ma Em orcentagem: a e , , ,86 % Força de rotensão aós o encurtamento elástico ( o ): 0, ( 5,495) 137,01 kn/cm 2 o a e o A 137,01. 9, ,2 kn o 9.6 DETERMINAÇÃO DE o NA ÓS-TRAÇÃO arte-se de i (força no macaco) deduzindo-se as seguintes erdas: atr erda or atrito ao longo da armadura;

41 α UNES (Bauru/S) 2139 Concreto rotendido 37 anc erda or escorregamento/acomodação dos fios na ancoragem; e erda or deformação imediata do concreto elo estiramento dos cabos restantes; r1 erda or relaxação inicial da armadura; cs1 erda or retração inicial do concreto; cc1 erda or fluência inicial do concreto. 9.7 ERDA OR ATRITO NA ÓS-TRAÇÃO (NBR 6118, item ) Considere um elemento ós-tracionado com uma armadura tensionada elo cilindro hidráulico na ancoragem ativa. Uma seção desta armadura, localizada a uma distância x da ancoragem ativa, terá uma tensão menor, devido a erdas de tensão geradas elo atrito entre a armadura e o duto (bainha), bem como entre também os rórios fios ou cordoalhas. i Força de atrito i - atr Figura 55 erda or atrito ao longo da bainha no estiramento da armadura. Nos elementos estruturais com ós-tração, a erda or atrito ode ser determinada or: atr ( µ Σα+ kx ) (x) [ 1 e ] i onde: i força de rotensão no macaco hidráulico; x abcissa do onto onde se calcula atr, medida a artir da ancoragem, em metros; Σα soma dos ângulos de desvio entre a ancoragem e o onto de abcissa x, em radianos; k coeficiente de ondulação coeficiente de erda or metro rovocada or curvaturas não intencionais do cabo. Na falta de dados exerimentais, ode ser adotado o valor 0,01µ (1/m); µ coeficiente de atrito aarente entre o cabo e a bainha. Na falta de dados exerimentais, ode ser estimado como a seguir (1/radianos): µ 0,50 entre cabo e concreto (sem bainha); µ 0,30 entre barras ou fios com mossas ou saliências e bainha metálica; µ 0,20 entre fios lisos ou cordoalhas e bainha metálica; µ 0,10 entre fios lisos ou cordoalhas e bainha metálica lubrificada; µ 0,05 entre cordoalha e bainha de oliroileno lubrificada; A Tabela 8 aresenta os valores roostos elo ACI 318 ara k e µ.

42 38 Tabela 8 - Valores roostos elo ACI ara k e µ. Tio de armadura k (or m) µ Armaduras em bainha flexível de metal: - fios... - cordoalha de 7 fios... - barras de alta resistência... 0,0033 0,0049 0,0016 0,0066 0,0003 0,0020 0,15 0,25 0,15 0,25 0,08 0,30 Cordoalha de 7 fios em dutos metálicos rígidos 0, ,15 0,25 Armadura engraxada: - fios e cordoalhas de 7 fios... 0,0010 0,0066 0,05 0,15 Exemlo 1) Qual a erda total or atrito devido à curvatura e à oscilação da bainha metálica flexível, de uma viga ós-tensionada armada com cordoalhas C 190 de 7 fios. Dados: i 0,74 f tk 0, Ma µ 0,20 (bainha metálica com cordoalha); k 0,006/m conforme valor roosto elo ACI (Tabela 8) y i i - atr 28 x l 2 l 2 l 15,2 m Figura 56 Esquema da viga. A 9,87 cm² Resolução α m tg 2 x 2 2m x x 2 x m 2y α 2 α 2 y α 4y tg 2 x arco circular m α 8y x Figura 57 Armadura curva. e ara ângulos equenos:

43 39 α 4y 2 x 8y α (rad) x α 0,147 rad 1520 Conforme a NBR 6118: atr (x) i ( µ Σα+ kx ) [ 1 e ] Força de rotensão no macaco hidráulico: i i. A 140,6. 9, ,7 kn atr atr ( 0,147 0,006.15,2) ( 0,1206 ) [ ] 0,20. + (15,2) 1387,7 1 e 1387,7 1 e (15,2) 157,7 kn 157,7 erda ercentual: , 4 % 1387,7 [ ] ortanto, na ancoragem assiva (extremidade direita da viga) a força de rotensão na armadura é: i atr 1387,7 ( 157,7) 1.230,0 kn 2) Calcular as erdas or atrito num cabo de uma viga contínua ós-tensionada, nas osições B, C e D. Considere: µ 0,20 (bainha metálica com cordoalha); k 0,002/m. D A ancoragem ativa α(a/b) B y B 0,47 C α(c/d) y D 0,185 E α(a/c) 9 m Figura 58 osicionamento da armadura de rotensão na viga rotendida. Resolução A erda de rotensão or atrito ode ser exressa também como erda de tensão: (x) i ( µ α+ kx) e Tensão e erda de rotensão em B:

44 40 8yB ,47 1 α( A / B) 0,104 rad x (9) e i ( 0,2. 0,104+ 0,002. 9) (9) 0,962 erda de 3,8 % (1 0,962) 100 i Tensão e erda de rotensão em C: 8yB 8. 0,47 α( A / C) 0,209 rad x 18 (18) e i ( 0,2. 0,209+ 0,002.18) (18) 0,925 erda de 7,5 % i Tensão e erda de rotensão em D: α (A / D) α (A / C) + α (C / D) 8yD ,185 1 α( A / D) α x (25) e i ( A / C) + 0, , 262 ( 0,2. 0,262+ 0, ) (25) 0,903 erda de 9,7 % i rad Exercício roosto Uma viga contínua com três vãos em a armadura em arábolas sucessivas. Assumindo µ 0,20, k 0,0025/m, i Ma, f tk Ma, E Ma calcule a tensão na armadura nas seções A até F. 14,64 m 3,65 3,65 4,70 D A 45,7 cm C 35,3 E F 32,3 B Figura 59 Esquema da viga.

45 ERDAS NA ANCORAGEM NA ÓS-TRAÇÃO A erda na ancoragem deve-se ao escorregamento dos fios, e deende do tio de disositivo de ancoragem. Decresce com o aumento da distância da ancoragem, odendo ser desrezível na seção mais solicitada, sendo, entretanto, imortante em eças curtas. Nos disositivos com cunhas, as erdas de rotensão são maiores (erda or encunhamento) e significativas. Segundo a NBR 6118 ( ), essas erdas devem ser determinadas exerimentalmente ou adotados os valores indicados elos fabricantes dos disositivos de ancoragem. Quando a armadura recua devido ao escorregamento/acomodação, surge um atrito contrário que faz com que a erda de tensão na armadura ocorra somente até uma distância X da ancoragem ativa. i,anc tensão antes do escorregamento,atr atrito tensão aós o escorreg. na ancoragem atrito /2,anc 0 X x Figura 60 erda de tensão or atrito e or escorregamento na ancoragem. A erda de tensão na osição da ancoragem é: δ,anc 2E (Lei de Hooke) X δ escorregamento/acomodação na ancoragem; δ com erda de deformação média até X. X Na osição X a erda de tensão é nula, e: X E i δ λ λ valor deendente da curvatura da armadura e do atrito (µ); i tensão na armadura na osição da ancoragem ativa (macaco hidráulico).

46 42 Linear i arabólico x Tabela 9 - Valores de λ e X ara erfis tíicos da armadura. µα + kx erfil λ X l x k X E k δ i i a b µ a 2 k b 2 + X E i δ λ Circular i R µ R + k X E i δ λ Qualquer forma, ou combinação de formas (modelo aroximado) (x) i z z 1 l i X E z l δ l x Exemlo Assumindo i Ma e δ 5,1 mm 0,0051 m, qual o valor de X e da erda de rotensão devida ao escorregamento na ancoragem ativa? Quais os valores das tensões na armadura de rotensão nas osições X e X/2? Dados: µ 0,15, k 0,0025/m, E Ma. 7,32 m 7,32 ancoragem ativa a 45,7 cm arábola Resolução Figura 61 Esquema da armadura na viga.

47 43 µ a 2. 0,15. 0,457 λ 2 + k + 0,0025 0,00506 /m 2 2 b 7,32 E δ ,0051 X 12, 31 m λ 130,3 0,00506 i A erda de rotensão é: δ 0,0051,anc 2E , 4 Ma X 12,31 162,4 erda ercentual: , 5 % 1303 i ,4,anc 1140,6 antes do escorreg. na ancoragem µ,anc ,2 aós o escorregamento , ( 162,4 2 ),anc 0 X 2 X 2 distância (x) X 12,31 osição do "macaco" i i - atr osição do "macaco" (anc. ativa) atrito no alongamento ancoragem assiva escorregamento (δ) atrito no escorregamento Figura 62 erda de tensão or atrito e or escorregamento na ancoragem. 9.9 ERDA DE ROTENSÃO NA ÓS-TRAÇÃO OR DEFORMAÇÃO IMEDIATA DO CONCRETO ELO ESTIRAMENTO DOS CABOS RESTANTES Na ós-tração os macacos de rotensão aóiam-se na rória eça a ser rotendida, o que imõe deformações na eça à medida que a armadura vai sendo estirada, de modo que não ocorrem erdas de rotensão quando os cabos são estendidos todos juntos. No entanto, quando a rotensão é alicada cabo or cabo, a rotensão num cabo rovoca deformações no concreto que resultam em erda de rotensão nos cabos já tracionados e ancorados.

48 44 O rimeiro cabo sofre erda de rotensão decorrente da rotensão dos n-1 cabos restantes, e assim sucessivamente, sendo zero a erda do último cabo estirado. Segundo a NBR 6118 (item ), a erda média de rotensão, or cabo, é: α ( + )( n 1) c 2n cg com: c tensão inicial no concreto ao nível do baricentro da armadura de rotensão, devido à rotensão simultânea dos n cabos; cg tensão no mesmo onto, devida à carga ermanente mobilizada ela rotensão ou simultaneamente alicada ela rotensão. α E E c ara um número muito grande de cabos, de modo aroximado: 1 α 2 ( + ) c cg 9.10 RETRAÇÃO E FLUÊNCIA INICIAL DO CONCRETO NA ÓS-TRAÇÃO A erda de rotensão or retração e fluência inicial do concreto ocorre quando os cabos de rotensão são rotendidos em instantes diferentes, ou seja, o cabo rotendido numa rimeira etaa já vai sofrendo erdas de rotensão até o instante de rotensão de cada um dos cabos restantes. As erdas de rotensão ocorridas entre as etaas de rotensão devem ser somadas à da relaxação da armadura. Não havendo necessidade de se considerar um cálculo mais refinado, essa erdas iniciais odem ser estimadas, ou desrezadas quando forem equenas DETERMINAÇÃO DA FORÇA DE ROTENSÃO FINAL A força de rotensão final ( ) é aquela existente aós ocorridas todas as erdas de rotensão. ode ser calculada subtraindo todas as erdas ocorridas aós a alicação da força o (erdas rogressivas osteriores: retração e fluência do concreto e relaxação da armadura) ERDA DE ROTENSÃO OR RETRAÇÃO DO CONCRETO A retração no concreto é afetada or muitos fatores: traço, tio de agregados, tio de cimento, temo de cura, temo de alicação da rotensão aós a cura, dimensões e forma da eça, condições do ambiente, etc. Aroximadamente 80 % da retração ocorre no rimeiro ano. A erda de tensão na armadura devida à retração do concreto ode ser aroximada or: onde: cs cs E cs deformação esecífica de retração do concreto ao nível da armadura, no temo considerado; E módulo de elasticidade da armadura de rotensão.

49 45 A deformação cs é fornecida ela NBR 6118 (Tabela 8.2, item ) do temo t o (dias) até o temo final (t ), odendo ser utilizada onde não for necessária grande recisão. Quando maior recisão for exigida ode-se alicar a formulação contida no Anexo A da NBR O Anexo A da norma trata do Efeito do temo no concreto estrutural, e informa que as rescrições têm caráter informativo que odem, na falta de dados melhores, ser usadas no rojeto de estruturas com concretos do gruo I da ABNT NBR 8953 cobertos or esta Norma. Outros valores odem ser usados, desde que comrovados exerimentalmente, or meio de ensaios realizados de acordo com Normas Brasileiras esecíficas, levando em conta variações nas características e roriedades dos comonentes do concreto, ou ainda desde que resaldados or Normas Internacionais ou literatura técnica VALOR DA RETRAÇÃO (Anexo A, NBR 6118, item A.2.3) Entre os instantes t o e t a retração é dada or: cs (t ; t o ) cs [β s (t) β s (t o )] onde: cs 1s. 2s cs valor final da retração; 1s coeficiente deendente da umidade relativa do ambiente e da consistência do concreto (ver Tabela A.1 da NBR 6118); 2s coeficiente deendente da esessura fictícia da eça. 2s h 20,8 + 3h fic fic onde: h fic esessura fictícia, em cm; h fic 2A γ µ ar c γ coeficiente deendente da umidade relativa do ambiente (U - %) Tabela A.1. ( 7,8 0,1U ) γ 1 + ex + A c área da seção transversal da eça; µ ar arte do erímetro externo da seção transversal da eça em contato com o ar; β s (t) ou β s (t o ) coeficientes relativos à retração, nos instantes t ou t o, dados na Figura A.3 da NBR 6118; t idade fictícia do concreto no instante considerado, em dias (ver item A da NBR 6118); t o idade fictícia do concreto no instante em que o efeito da retração na eça começa a ser considerado, em dias.

50 ERDA DE ROTENSÃO OR FLUÊNCIA DO CONCRETO A fluência no concreto ao nível da armadura deende da tensão no concreto naquele nível. Semelhantemente à erda or retração, a erda de tensão or fluência do concreto é: cc cc. E Onde não for necessária grande recisão, o coeficiente de fluência ϕ (t ; t o ), entre o temo t o e o temo final (t ), ode ser determinado na Tabela 8.2 da NBR 6118 (item ), e: cc c (t o ) ( t ;t o ) ϕ(t ;t o ) E ci,28 Quando for necessária maior recisão deve-se recorrer ao cálculo conforme descrito no Anexo A da NBR 6118, como aresentado a seguir Anexo A Fluência do Concreto (A.2.2) A deformação or fluência do concreto ( cc ) é comosta de duas artes, uma ráida e outra lenta. A deformação ráida ( cca ) é irreversível e ocorre durante as rimeiras 24 h aós a alicação da carga que a originou. A deformação lenta é, or sua vez, comosta or duas outras arcelas: a deformação lenta irreversível ( ccf ) e a deformação lenta reversível ( ccd ). cc cca + ccf + ccd cca deformação ráida irreversível, rimeiras 24 horas; ccf deformação lenta irreversível (umidade, consistência, esessura, idade); cca deformação lenta reversível, deende aenas da duração do carregamento. c,tot c + cc c (1 + ϕ) ϕ ϕ a + ϕ f + ϕ d c,tot deformação total do concreto; ϕ coeficiente de fluência; ϕ a coeficiente de deformação ráida; ϕ f coeficiente de deformação lenta irreversível; ϕ d coeficiente de deformação lenta reversível. Valor da Fluência (A.2.2.3) No instante t a deformação devida à fluência é dada or: cc (t ; t o ) cca + ccf + ccd c ϕ (t ;t o ) E c,28 com o módulo de elasticidade tangente inicial ara j 28 dias (E c,28 ), obtido em ensaio segundo a NBR 8522 ou calculado ela exressão E c,28 E ci,28 α E 5600 fck. O coeficiente de fluência ϕ (t ; t o ) é dado or: