Introdução à Física Computacional
|
|
|
- Gilberto Martinho Figueiroa
- 8 Há anos
- Visualizações:
Transcrição
1 Introdução à Física Computacional Apostila preparada para a disciplina de Modelos Computacionais da Física I, ministrada para o Curso de Licenciatura em Física do Departamento de Física, Instituto de Física e Matemática, Fundação Universidade Federal de Pelotas, Pelotas - S. Início: Outubro de 006. Versão: de julho de 009
2
3 Sumário eferências Bibliográficas iii 1 epresentação de Números e Erros Fontes de erros e incertezas epresentação de números em diferentes bases epresentação de números inteiros e conversões de base epresentação de números reais e conversões de base Conversão de números inteiros da base b para a base decimal Algoritmo de Horner Divisão de uffini Conversão de números fracionários da base b para a base decimal Algoritmo de Horner Divisão de uffini Operações com números binários Adição binária Subtração binária Multiplicação binária epresentação de números em computadores digitais epresentação de números inteiros epresentação de números reais Erros na representação e na álgebra de ponto flutuante Precisão e acurácia Erros absoluto e relativo Erro absoluto Erro relativo Erros na representação: arredondamento e truncamento Número de dígitos significativos Erros na álgebra de ponto flutuante Erros de arredondamento Erros de truncamento Análise de erros de ponto flutuante Derivação Numérica 7.1 Introdução Fórmulas clássicas de diferença finita Fórmula de diferença adiantada forward difference) Fórmula de diferença atrasada backward difference) Fórmula de diferença centrada centered difference) Fórmula de 5 pontos Fórmulas de diferenças finitas para a derivada segunda Fórmula de três pontos Fórmula de cinco pontos Fórmulas para o cálculo de derivadas em pontos fora da rede Derivada de três pontos Derivada de quatro pontos Derivada de cinco pontos Extrapolação de ichardson e estimativa de erro i
4 ii SUMÁIO 3 Integração Numérica Introdução Fórmulas de Newton-Cotes Fórmulas fechadas de Newton-Cotes egra trapezoidal N = 1) egra de Simpson N = ) egra de Simpson dos 3/8 N = 3) egra de Bode N = 4) egras em ordens mais altas N 5) Fórmulas abertas de Newton-Cotes Fórmulas fechadas estendidas egra trapezoidal estendida egra de Simpson estendida Estimativas de erro nas fórmulas de Newton-Cotes Quadratura gaussiana Idéia básica na quadratura gaussiana Fórmulas gaussianas clássicas Fórmula de Gauss-Legendre Fórmula da Gauss-Chebyshev Fórmula de Gauss-Laguerre Fórmula de Gauss-Hermite Integração automática e adaptativa Integração de omberg Integração automática usando quadraturas gaussianas Integração adaptativa Soluções de Equações Não Lineares Introdução Métodos iterativos para o cálculo de raízes reais Método da bisecção Método da falsa posição Método da secante Método de Newton-aphson aízes complexas de funções analíticas O método de Müller Problemas de Valor Inicial [Em Construção] Introdução Equações de diferenças finitas lineares Integração numérica por série de Taylor O método de Euler O Método de unge-kutta O Método de unge-kutta de segunda ordem ou o Método do ponto médio O Método de unge-kutta de quarta ordem Sistemas de equações diferenciais Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
5 eferências Bibliográficas [1] Intel fortran compiler for linux, Acesso em: 01 jun [] M. Abramowitz and I. A. Stegun, Handbook of mathematical functions, Dover, New York, [3] S. D. Conte and C de Boor, Elementary numerical analysis. an algorithmic approach, third ed., International series in pure and applied mathematics, McGraw-Hill, New York, 1980, 43 + xii pp. [4] M. Cristina C. Cunha, Métodos Numéricos, segunda ed., Unicamp, Campinas, 000, 16 pp. [5] udi Gaelzer, Introdução ao Fortran 90/95, rudi/grad/modcomp/apostila/apostila.html, Pelotas, November 006, vi pp. [6] D. Goldberg, What every computer scientist should know about floating point arithmetic, ACM Computing Surveys ), [7] Sebastião Cícero Pinheiro Gomes, Métodos Numéricos: Teoria e Programação, FUG, io Grande, 1999, 190 pp. [8] Joe D. Hoffman, Numerical methods for engineers and scientists, second ed., Marcel Dekker, New York, 001, 83 + xi pp. [9] ubin H. Landau and Manuel José Páez Mejiá, Computational physics. Problem solving with computers, John Wiley & Sons, New York, 1997, xviii pp. [10] D. E. Müller, A method of solving algebraic equations using automatic computer, Mathematical Tables and Other Aids to Computation ), [11] Tao Pang, An introduction to computational physics, second ed., Cambridge University Press, New York, 006, xvi pp. [1] W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical recipes in fortran 90, Fortran Numerical ecipes, vol., Cambridge, New York, 1997, 55 pp. [13] John. ice, Numerical Methods, Software, and Analysis, McGraw-Hill, New York, 1983, xii pp. [14] Germán amón Canahualpa Suazo, Apostila de Cálculo Numérico, DME - IFM - UFPel, Pelotas, November 004, vii pp. [15] David M. Young and obert Todd Gregory, A Survey of Numerical Mathematics, vol. I, Dover, New York, 1988, x pp. iii
6 iv EFEÊNCIAS BIBLIOGÁFICAS Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
7 Capítulo 1 epresentação de Números e Erros Neste capítulo serão considerados aspectos básicos a respeito do cálculo numérico: a representação de números inteiros e de ponto flutuante em código binário e as fontes de erros que invariavelmente ocorrem quando se faz necessário usar uma representação finita para representar um número ou uma função matemática que, em geral é transcendental e/ou necessita de uma soma ou produto infinito de números para ser exatamente representado. 1.1 Fontes de erros e incertezas Embora sempre se busque soluções exatas aos problemas que enfrentamos, raramente atingimos o nosso objetivo. Erros e incertezas podem ser introduzidos em cada etapa da formulação e solução de problemas. A natureza das incertezas que surgem quando se busca a solução de um problema será abordada neste capítulo. Simultaneamente, os erros introduzidos pela computação numérica, destinada a buscar a solução desejada, serão examinados com um certo grau de detalhe. O processo de solução de um problema é dividido em três fases: 1. Formulação precisa de um modelo matemático e o seu modelo numérico relacionado.. Construção de um método destinado a resolver o problema numérico. 3. Implementação de um método para calcular a solução. Na discussão que será feita a respeito das fontes de erro em cálculo numérico, não serão considerados erros triviais que podem ser evitados, tais como copiar uma fórmula erroneamente ou realizar um erro de sintaxe na programação, muito embora tais erros ocorram e perfaçam uma fração considerável do esforço e do tempo dispendidos ao se trilhar as três fases mencionadas acima. Neste capítulo estaremos somente interessados nos erros que resultam ser inevitáveis, dada a própria natureza da representação finita de números em um computador e/ou da implementação numérica de um determinado cálculo. As incertezas introduzidas contaminam a solução e é importante tentar-se balancear as incertezas. Se a incerteza no modelo matemático é de 1%, então não faz sentido a implementação de um modelo numérico e de um método que atinja 6 dígitos de precisão, por exemplo. O diagrama da figura 1.1 ilustra o processo usualmente percorrido quando se busca uma solução para um problema físico real a partir de uma modelagem, inicialmente matemática, seguida por uma modelagem computacional e, finalmente, passando pela implementação do método numérico a partir da modelagem computacional, seguida pela obtenção dos resultados. As incertezas ocorrem desde a fase de modelagem matemática até a solução numérica. Neste capítulo, serão abordadas algumas fontes de incertezas na etapas de modelagem computacional e implementação do método numérico. 1. epresentação de números em diferentes bases Nesta seção serão discutidos alguns métodos para a mudança de base na representação de números, tanto inteiros quanto reais. É fato comum para grande parte dos computadores atualmente empregados na modelagem computacional o emprego de uma base numérica distinta da base decimal, à qual o seres humanos tendem a se apegar. Em geral, os números são armazenados na base binária), existindo ainda plataformas que os armazenam na base 8 octal) ou na base 16 hexadecimal). A representação de números inteiros é ligeiramente distinta da representação de números reais. 1
8 ÈÖÓ Ð Ñ Ê Ð ÓÖÑÙÐ Ó Ó ÅÓ ÐÓ Å Ø Ñ Ø Ó ÆÙÑ Ö Ó 1.. epresentação de números em diferentes bases ÓÒ ØÖÙÓ ÓÅ ØÓ Ó ÁÑÔÐ Ñ ÒØ Ó ÓÅ ØÓ Ó ÁÒ ÖØ Þ ËÓÐÙÓ Figura 1.1: Diagrama que representa o processo de solução numérica de um problema físico real, indicando em que etapas entram as incertezas epresentação de números inteiros e conversões de base De uma forma geral, um número inteiro N é representado, na base b, por um conjunto de dígitos a i, i = 0, 1,,... ), sendo que a i assume um intervalo de valores determinado pela base em uso. A tabela 1.1 indica estes valores para as bases mais utilizadas, inclusive para a base decimal. Há no mínimo duas maneiras de se representar o número N. O sistema posicional agrupa os dígitos na forma de uma seqüência, na qual a magnitude da contribuição de cada dígito ao número depende da posição relativa que este ocupa. Neste sistema, o número N é escrito como: N = a n a n 1... a 1 a 0 ) b. A contribuição de cada dígito para o valor de N fica explicitada na forma polinomial, onde N é escrito como: N = a n b n + a n 1 b n a 1 b + a ) Até este momento, N tem sido tratado de uma forma abstrata. Por uma questão evolutiva, N tende a ser visto como um número na base 10 decimal), N = a n a n 1... a 1 a 0 ) 10 a n a n 1... a 1 a 0. Caso se passe a representar N sempre na base decimal, então deve-se abordar as outras representações do ponto de vista de conversões de ou para a base 10. Método das divisões sucessivas Considera-se inicialmente a conversão de um inteiro da base decimal para a base binária, uma vez que esta será a representação mais provável em um computador. Para realizar-se esta conversão de uma maneira prática, pode-se usar o método das divisões sucessivas, no qual N e os sucessivos quocientes q i são divididos por, sendo coletados os restos r i = 0, 1 até que o último quociente seja q n = 0, 1: Tabela 1.1: Intervalos de valores para os dígitos a i da base b. b a i 0, 1 8 0, 1,, 3, 4, 5, 6, , 1,, 3, 4, 5, 6, 7, 8, , 1,, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
9 Capítulo 1. epresentação de Números e Erros 3 N r 0 q 1 r 1 q r q 3... O último quociente q n ) somente será 0 se N = 0. Então, q n 1 r n 1 q n N = q n r n 1... r r 1 r 0 ) ou N = q n n + r n 1 n r + r r 0 0. Como exemplos, temos 1 = 1100) 5 = 11001) 315 = ). O mesmo método pode ser utilizado para converter N para qualquer base b; divide-se N e os sucessivos quocientes q i por b até que o último quociente seja um inteiro 0 q n b 1: N b r 0 q 1 b r 1 q b r q 3... q n 1 r n 1 b q n Desta forma, N = q n r n 1... r r 1 r 0 ) b = q n b n + r n 1 b n r b + r 1 b 1 + r 0 b 0. Assim, 1 = 14) 8 = C) 16 5 = 31) 8 = 19) = 473) 8 = 13B) 16. O programa 1.1 implementa o método das divisões sucessivas para a conversão de qualquer número inteiro da base 10 para a base. 1.. epresentação de números reais e conversões de base Dado agora um número real X, o qual possui uma parte inteira X i e uma parte fracionária X f = X X i, utiliza-se novamente o método das divisões sucessivas para X i, enquanto que para X f usa-se o Método das Multiplicações Sucessivas: multiplica-se X f por, extraindo-se a parte inteira do resultado a qual pode ser 0); o restante é novamente multiplicado por, repetindo-se o processo até que o resto fracionário seja 0 ou que se obtenha um padrão repetitivo, em cujo caso o número fracionário será periódico. Este método será ilustrado com dois exemplos. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
10 4 1.. epresentação de números em diferentes bases Programa 1.1: Converte um número da base 10 para a base. Caso o número seja negativo, o bit de sinal é utilizado. program conversor implicit none integer, parameter : : base= integer : : i, j, qn, rn, num, num_abs real, parameter : : log= integer, DIMENSION : ), ALLOCATABLE : : b! write, fmt= a ), advance= no ) Numero na base 1 0 : read, num select case num) case 0 ) allocate b 1 ) ) b= 0 case : 1)!! Neste caso, o v e t o r i r a a l o c a r um d i g i t o a mais e a t r i b u i r o v a l o r 1! ao ultimo d i g i t o, como convencao para s i n a l n e g a t i v o.! num_abs= abs num) j= l o g real num_abs ) ) / log allocate b 0 : j + 1 ) ) qn= num_abs do i= 0, j rn= mod qn, base ) qn= qn/ base b j i + 1)= rn end do b0)= 1 case 1 : ) j= l o g real num) ) / log allocate b 0 : j ) ) qn= num do i= 0, j rn= mod qn, base ) qn= qn/ base b j i )= rn end do end select j= size b ) write, fmt= "A forma b i n a r i a e : " ), advance= no ) do i= 1, j 1 write, fmt= i 1 ), advance= no ) b i 1) end do write, fmt= i 1 ) ) b j 1)! end program c o n v e r s o r Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
11 Exemplo 1.1. Capítulo 1. epresentação de Números e Erros 5 Seja X f = 0, 815, então 0, 815 1, 650 0, 650 1, 500 0, 500 0, 500 0, , 0000 Ou seja, 0, 815 = 0, 1101). O exemplos a seguir mostram a dificuldade de se obter a representação de um número fracionário em outra base. Exemplo 1.. Um exemplo interessante é o número X f = 0, 1. Neste caso, 0, 1 0, 0, 0, 4 0, 4 0, 8 0, 8 1, 6 0, 6 1, 0, 0, 4 e o processo de multiplicações sucessivas repete a seqüência de dígitos 0011 ad infinitum. Portanto, 0, 1 = 0, ). Exemplo 1.3. Seja X f = 0, 55, então 0, 55 1, , , , , , , , , , , 300 0, , , 300 0, , , 700 0, , 800 0, 700 1, , 800 0, , , , , 100 0, , , 100 0, 400 0, , 500 0, 400 0, , 500 1, , , 9600 Ou seja, 0, 55 = 0, ). Este exemplo mostra que em um computador, onde o espaço para representação de um número é finito, este número terá que ser arredondado. A forma polinomial de um número fracionário é dada por: X f = α α + α Portanto, um número real X = X i + X f pode ser representado na base por X = a n n + a n 1 n a α α + α = a n a n 1... a 0, α 1 α α 3... ). Exemplo 1.4. Seja X = 75, 8, temos X i = 75 = ) e Portanto, X f = 0, 8 = 0, ). 75, 8 = , ). Para converter um número fracionário da base decimal para uma base b, também aplica-se o método das multiplicações sucessivas, que, neste caso, consiste em multiplicar o número por b e extrair a parte inteira podendo ser 0). O resto fracionário é multiplicado novamente por b e a parte inteira é extraída. Este processo deve ser repetido até sobrar o resto igual a 0 ou até se observar um padrão repetitivo. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
12 6 1.. epresentação de números em diferentes bases 1..3 Conversão de números inteiros da base b para a base decimal Para introduzir a conversão para a base decimal, será usada novamente a base binária como um primeiro exemplo. Seja o número N, representado por N = a m a a 1 a 0 ), a sua representação na base decimal pode ser obtida simplesmente pela soma do polinômio N = a m m + + a + a a 0. A operacionalização desta soma pode ser obtida pelos seguintes algoritmos: Algoritmo de Horner. O número N pode ser obtido na base decimal através do cálculo da seqüência b m = a m, b m 1 = a m 1 + b m, b m = a m + b m 1,... b 1 = a 1 + b, b 0 = a 0 + b 1. E então, N = b Divisão de uffini. Equivalente ao método anterior, diferindo somente na disposição dos coeficientes a i e b i : a m a m 1 a a 1 a 0 b m b 3 b b 1 b m b m 1 b b 1 b 0 e, novamente, Exemplo 1.5. N = b 0. Seja o número 11101). Então, a partir da seqüência de Horner, b 4 = a 4 = 1, b 3 = a 3 + b 4 = = 3, b = a + b 3 = = 7, b 1 = a 1 + b = = 14, b 0 = a 0 + b 1 = = 9. A partir da divisão de uffini, Portanto, ) = 9. Esta metodologia pode ser generalizada para converter qualquer número inteiro na base b para a base decimal. Considere o número N = a m... a a 1 a 0 ) b. Usando o Algoritmo de Horner, por exemplo, temos a seqüencia c m = a m, Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
13 Capítulo 1. epresentação de Números e Erros 7 c m 1 = a m 1 + bc m, c m = a m 1 + bc m 1,... c 1 = a 1 + bc, c 0 = a 0 + bc 1 e, novamente, N = c Conversão de números fracionários da base b para a base decimal Considere um número fracionário com representação finita na base binária: O seu valor na base decimal será dado por X f = 0, α 1 α... α n ). X f = α α + + α n n. Esta soma pode ser calculada diretamente ou utilizando qualquer um dos dois métodos enunciados na seção 1..3, com algumas modificações Algoritmo de Horner. No caso de um número fracionário, o algoritmo fica b n = α n, b n 1 = α n b n, b n = α n + 1 b n 1,... b = α + 1 b 3, b 1 = α b, b 0 = 1 b 1. Então, N = b Divisão de uffini. No case de um número fracionário, 1 a m a m 1 a a b 1 m b 1 3 b 1 b 1 b m b m 1 b b 1 b 0 Exemplo 1.6. O número 0, 10111), pelo Algoritmo de Horner, fica b 5 = α 5 = 1, b 4 = α b 5 = = 3, b 3 = α b 4 = = 7 4, b = α + 1 b 3 = = 7 8, Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
14 8 1.. epresentação de números em diferentes bases b 1 = α b = = 3 16, Portanto, b 0 = 1 b 1 = , 10111) = 3 = 0, Uma outra situação que pode ocorrer é quando o número binário for infinito, por exemplo, através de uma seqüência de dígitos periódicos: X f = 0, α 1 α... α n β 1 β... β m ), onde β 1 β... β m indica que a seqüência de dígitos β 1 β... β m se repete ad infinitum. Na base decimal, tal número é dado por X f = α α + + α n n + β 1 n 1 + β n + + β m n m Observa-se que este número pode ser escrito como + β 1 n m 1 + β n m + + β m n m + β 1 n m 1 + β n m + + β m n 3m +. X f = α α + + α n n + β β + + β m m) n + β β + + β m m) n m + β β + + β m m) n m + β β + + β m m) n 3m +, X f = α 1 1 +α + +α n n + β β + + β m m) n 1 + m + m + 3m + ). Usando agora a identidade, temos obtém-se 1 1 x = 1 + x + x + x 3 +, para x < 1), 1 + m + m + 3m + = 1 m = 1 m m 1, X f = α α + + α n n + β β + + β m m) m n m 1. As duas expressões entre parênteses têm a mesma forma e podem ser calculadas diretamente usando qualquer um dos métodos descritos anteriormente. Exemplo 1.7. O número fracionário tem o seu valor na base decimal dado por X f = 0, ) = 0, ) X f = ) ) 3 1 = ) = 3 8 = 0, = 0, Em geral, se o número fracionário tem representação infinita periódica na base b, então o seu valor decimal será dado por X f = 0, α 1 α... α n β 1 β... β m )b, X f = α 1 b 1 + α b + + α n b n + β 1 b 1 + β b + + β m b m) b m n b m 1, onde as expressões entre parênteses podem ser calculadas diretamente ou utilizando quaisquer um dos métodos descritos anteriormente. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
15 Capítulo 1. epresentação de Números e Erros Operações com números binários Como a maioria dos computadores usa a base b =, estes executam operações aritméticas em números que estão na representação binária. Para tanto, as seguintes tabelas de operações são automaticamente satisfeitas Adição binária Uma adição no sistema binário é realizada da mesma forma que a adição no sistema decimal, lembrando que, no sistema binário, há apenas dígitos. Esta operação é realizada de acordo com a seguinte tabela de adição: Para somar números com mais de algarismos, o mesmo processo de transporte para a coluna posterior, utilizado na adição decimal, é empregado. Por exemplo, se 1 = 01) e 3 = 11), então = 01) + 11) = 100) = 4. Outro exemplo, se 10 = 1010) e 15 = 1111), então 1.3. Subtração binária = 1010) ) = 11001) = 5. A subtração é análoga à adição, sendo realizada de acordo com a tabela: Deve-se ressaltar que a operação 0-1 resulta em 1, porém com o transporte de 1 para a coluna à esquerda, que deve ser acumulado ao subtraendo e, por conseqüência, subtraído do minuendo. Por exemplo, se 7 = 111) e 4 = 100), então 7 4 = 111) 100) = 11) = 3. Outro exemplo, se 10 = 1010) e 8 = 1000), então Multiplicação binária 10 8 = 1010) 1000) = 10) =. Procede-se como em uma multiplicação no sistema decimal, de acordo com a tabela de multiplicação: Por exemplo, se 6 = 11010) e = 10), então = 11010) 10) = ) = 5. A divisão binária é um procedimento um tanto mais complicado e não será abordado aqui. 1.4 epresentação de números em computadores digitais Nesta seção serão apresentadas algumas das representações usadas para armazenar números inteiros ou reais na memória de um computador. As representações de números inteiros ou reais apresentadas na seção 1. não são suficientes; é necessário distingüir-se, por exemplo, o sinal do número. Como não existe a representação de um sinal + ou na memória de um computador, o recurso utilizado é acrescentar um bit adicional, para computadores binários, ao número para representar o sinal. Este bit é denominado bit de sinal. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
16 epresentação de números em computadores digitais epresentação de números inteiros A representação mais direta de números inteiros é denominada Sinal-Módulo. Nesta representação, o valor absoluto do número inteiro é obtido diretamente a partir dos algoritmos discutidos na seção 1., enquanto que o sinal é representado por um dígito adicional colocado à esquerda do número. Quando a representação é binária, o bit de sinal é dito ocupar a posição do bit mais significativo. Então, supondo que a memória do computador disponha de q dígitos para a representação, um número inteiro na base b será representado pelo computador através da seqüência de dígitos a q 1 a q... a 1 a 0, 1.) sendo {a 0, a 1,..., a q 1 } {0, 1,..., b 1}, com a q 1 representando o sinal do número. Esta seqüência de dígitos é denominada palavra. Por exemplo, no sistema binário convenciona-se usar a q 1 = 0 para + e a q 1 = 1 para. A conversão do número internamente representado por 1.) para o sistema decimal é realizado através de uma fórmula semelhante à forma polinomial 1.1): sendo N o número inteiro na base decimal. s o sinal ou +1 ou 1). q N = s a k b k, 1.3) q 1 o número de dígitos disponível para representar o valor absoluto de N. b a base, às vezes denominada de radix um inteiro maior que 1). a k um dígito válido na representação 0 a k < b), k = 0, 1,..., q 1. Os valores em questão para as quantidades em 1.3) dependem da arquitetura e do compilador em uso. k=0 Exemplo 1.8. O compilador Intel Fortran 95 [1] possui 4 modelos de representação de inteiros com 1,, 4 e 8 bytes, também denominados de espécies. Sendo para todos os casos b =, o valor absoluto do maior número inteiro que pode ser representado internamente para cada espécie N p max, p = 1,, 4, 8) é, a partir de 1.3), N p max = 8p k=0 17, para p = 1; k = p = 8p , para p = ; 1 = , para p = 4; , para p = 8. Outras representações de números inteiros em computadores existem, como por exemplo as representações complemento de 1 ou complemento de [15]; porém, estas não serão discutidas aqui. A representação de um número inteiro em um computador é exata. Operações aritméticas entre números inteiros também é exata, sob as seguintes condições: 1. o resultado não pode se encontrar fora do intervalo de números inteiros que podem ser representados;. a divisão somente pode ser realizada entre números exatamente divisíveis, isto é, a parte fracionária deve ser nula epresentação de números reais A representação de números reais em computadores, também denominada representação de ponto flutuante. Em uma representação de ponto flutuante, um número é representado internamente através de uma notação científica, isto é, por um bit de sinal s interpretado como positivo ou negativo), um expoente inteiro exato e e uma mantissa inteira positiva M, sendo que um número limitado de dígitos é permitido para e e M. Tomando todas estas quantidades juntas, estas representam o número x = s 0, d 1 d... d n ) b e, 1.4) Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
17 Capítulo 1. epresentação de Números e Erros 11 s expoente de 8 bits mantissa de 3 bits 1 = {}}{ { }} { { }} { = = = Figura 1.: epresentações de ponto flutuante para alguns números em uma palavra típica de 3 bits 4 bytes). Espécie EAL4) EAL8) EAL16) n e min e max x min 1, , , x max 3, , , x eps 1, , , Tabela 1.: Valores de n, e min, e max, x min, x max e x eps para o compilador Intel Fortran. o qual está escrito em uma forma legível para seres humanos. Além das quantidades já definidas, em 1.4) os dígitos d 1, d,..., d n são limitados pela base b e o expoente é limitado ao intervalo e min e e max. Adicionalmente, n 1 é denominado de número de dígitos do sistema e define o tamanho da mantissa M = 0, d 1 d... d n. Contudo, um computador somente pode representar os valores de e e E através de dígitos na base b. Um computador digital b = ), por exemplo, dispõe sempre de um tamanho de palavra finito, isto é, o número total de bits que podem ser utilizados para representar s 1 bit), a parte exponencial e a mantissa é sempre fixo, para uma dada espécie de variável real. Um número real de precisão simples, por exemplo, é tipicamente representado por uma palavra de 4 bytes ou 3 bits, sendo que 1 bit é utilizado para representar o sinal, enquanto que 8 bits são utilizados para representar a parte exponencial, restando 3 bits para representar a mantissa. Desta forma, tal número será representado na memória do computador como x = se 7 e 6 e 5 e 4 e 3 e e 1 e 0 d 3 d... d d 1, onde {s, e 0,..., e 7, d 1,..., d 3 } = {0, 1}. A figura 1. ilustra representações em 4 bytes de alguns números. Uma descrição mais aprofundada acerca da representação binária de números em computadores digitais pode ser obtida em [15, seção.5]. A conversão do número x representado em 1.4) para a base decimal pode ser realizada pela fórmula polinomial n x = s b e d k b k. Como exemplo, a tabela 1. mostra os valores de n, e min e e max para o compilador Intel Fortran. Para uma base b qualquer, denotando este sistema pelo símbolo observam-se as seguintes características: k=1 x [b, n, e min, e max ], O menor número positivo que pode ser representado neste sistema é x min = 0, 1 b emin = b emin 1. Valores para x min válidos para o compilador Intel Fortran são apresentados na tabela 1.. Isto significa que qualquer número x tal que x min < x < x min não poderá ser representado pelo computador. Esta ocorrência é denominada underflow. Os compiladores podem ser instruídos ou a parar o processamento neste ponto, disparando uma mensagem de erro, ou a seguir o processamento arredondando x = 0. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
18 epresentação de números em computadores digitais O maior número positivo que pode ser representado neste sistema é x max = 0, b 1) b 1)... b 1) b emax = b 1) } {{ } n vezes n ) b k b emax = 1 b n) b emax. Valores para x max válidos para o compilador Intel Fortran são apresentados na tabela 1.. Isto significa que qualquer número x tal que k=1 x < x max ou x > x max não poderá ser representado pelo computador. Esta ocorrência é denominada overflow. Os compiladores usualmente tomam duas possíveis providências quando detectam um overflow; ou páram o processamento do programa emitindo uma mensagem de erro, ou continuam o processamento atribuindo a x o valor simbólico x = Infinito ou x = Infinito. O maior número que pode ser somado ou subtraído a 1,0, com o resultado permanecendo indistingüível de 1,0 é x eps = b 1 n. 1.5) Os valores de x eps para o compilador Intel Fortran são também apresentados na tabela 1.. A quantidade x eps também é denominada de epsilon da máquina ɛ m ) ou de precisão da máquina. Somente um conjunto finito F de números racionais podem ser representados na forma 1.4). Os números neste conjunto são denominados números de ponto flutuante. Para uma representação normalizada d 1 0), este conjunto contém precisamente números racionais. b 1) e max e min + 1) b n Exemplo 1.9. Considere um modelo simplificado de representação numérica de ponto flutuante dado por x [, 4, 5, 6]. Para este sistema: o menor número positivo possível é: x min = 0, 1000) 5 = 5 1 = 1 64 ; ou seja, a região de underflow consiste no intervalo O maior número positivo possível é: 1 64 < x < x max = 0, 1111) 6 = 1 4) 6 = 60; ou seja, as regiões de overflow consistem nos intervalos x < 60, x > 60. O maior número que pode ser somado ou subtraído de 1,0 e que mantém o resultado inalterado é: x eps = 1 4 = 1 8. O número de elementos em F é: ) = 193. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
19 Capítulo 1. epresentação de Números e Erros 13 Figura 1.3: Números normalizados positivos representáveis em x [, 3, 1, ]. Os riscos verticais posicionam os números. Para cada número positivo, existe um correspondente número negativo. Exemplo Considere o sistema de números de ponto flutuante x [, 3, 1, ]. Para este sistema: o menor número positivo possível é: x min = 1 1 = 1 4. ou seja, a região de underflow consiste no intervalo O maior número positivo possível é: 1 4 < x < 1 4. x max = 1 3) = ou seja, as regiões de overflow consistem nos intervalos x < 7, x > ) 4 = 7 8 ; O maior número que pode ser somado ou subtraído de 1,0 e que mantém o resultado inalterado é: x eps = 1 3 = 1 4. O número de elementos em F é: ) = 33. A fração positiva dos números possíveis em x [, 3, 1, ] está indicada na figura 1.3. Cada risco vertical posiciona um números representável neste sistema. 1.5 Erros na representação e na álgebra de ponto flutuante Nesta seção será feita uma breve descrição dos principais erros envolvidos na representação de pontos flutuantes e nas operações algébricas entre os mesmos Precisão e acurácia Os conceitos de precisão e acurácia são amiúde confundidos entre si. A diferença entre ambos é oriunda da diferença entre o hardware e o software à disposição do programador. Precisão 1 refere-se ao quão próximo um número representado pelo computador representa o número que ele ambiciona representar. A precisão de um número é governada pelo número de dígitos empregados na representação e na álgebra. Assim, a constante π será representada com maior precisão utilizando 8 bytes do que utilizando 4 bytes para armazenar o número ver tabela 1.). Acurácia refere-se a quão próximo um número representado pelo computador como resultado de uma série de operações, por exemplo) está do valor correto do número que ele almeja representar. A acurácia é governada pelos erros de truncamento e arredondamento) no método numérico empregado. Assim, se os números π 1 = 3, e π = 3, almejam ambos a representar o número π = 3, , o número π possui maior acurácia que π 1, embora ambos possuam a mesma precisão. Com freqüência, em linguagem coloquial refere-se à precisão quando na verdade o correto seria referir-se à acurácia de um resultado. As seções a seguir indicam como se pode medir a acurácia de um número através do cálculo dos erros absoluto e relativo do mesmo. 1 Do inglês precision. Do inglês accuracy. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
20 Erros na representação e na álgebra de ponto flutuante 1.5. Erros absoluto e relativo São duas medidas relacionadas entre si, largamente empregadas na análise de erro numérico Erro absoluto Seja X o valor exato não conhecido) de um número e fl X) o seu valor aproximado conhecido) por uma representação de ponto flutuante. O erro absoluto EA X ) é definido como o valor absoluto da diferença entre o valor exato e o valor aproximado: EA x = X fl X). Ou seja, conhecendo-se fl X) e EA X, pode-se afirmar que X = fl X) ± EA x. Em geral, somente é possível estimar-se o valor do erro absoluto. Por exemplo, Arquimedes estimou o valor de π através da média do perímetro de polígonos que estavam contidos em uma circunferência de raio unitário e de polígonos que continham a circunferência. Fazendo uso deste método, Arquimedes foi capaz de estimar π min = 3, 1409 = < π < π max = = 3, Desta forma, Arquimedes obteve erros absolutos iguais a EA π = 6, para π min, EA π = 1, para π max e EA π =, para a média entre π min e π max. Portanto, Arquimedes poderia afirmar que π = 1 π min + π max ) ± 1 π max π min ) = 3, ± 0, Erro relativo Seja X o valor exato de um número e fl X) o seu valor aproximado, o erro relativo E X ) é definido como o erro absoluto dividido por fl X) : E X = EA X fl X) = X fl X) fl X) Voltando ao exemplo anterior, os erros relativos das estimativas de Arquimedes foram: E π =, para π min, E π = 3, para π max e E π = 8, para a média. Em geral, a melhor medida para se estimar a precisão de uma aproximação é o erro relativo, pois este indica diretamente o número de dígitos significativos corretos na aproximação Erros na representação: arredondamento e truncamento O tamanho finito da palavra utilizada em um computador digital para a representação de números de ponto flutuante provoca o surgimento de diversos tipos de erros, tanto na representação destes números quanto na álgebra que os envolve. Uma estratégia que reduz estes erros, empregada na maior parte dos computadores, consiste em empregar números de ponto flutuante normalizados, isto é, números cuja mantissa M está sempre dentro do intervalo 1 b M < 1, ou seja, 0, 5 M < 1 para computadores de base b =. Esta providência diminui o número de zeros à direita da vírgula e maximiza o número de dígitos não nulos utilizados para representar um dado número. Entretanto, mesmo em um sistema com representação normalizada, nem todos os números reais podem ser representados. Utilizando novamente o exemplo do sistema x [, 4, 5, 6], o número racional y = 0, não pode ser exatamente representado. A forma de y em base é:. y = 0, = 0, ). Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
21 Capítulo 1. epresentação de Números e Erros 15 Para escrever y de acordo com o sistema x [, 4, 5, 6], deve-se primeiro normalizar de acordo com as operações: y) = = ) = 0, ) 3, o qual está agora na forma normalizada. De acordo com 1.4), podemos identificar então M = 0, , e = 3. Contudo, para o sistema x [, 4, 5, 6] pode-se usar somente 4 dígitos na mantissa. aproximação possível para y) fica: Desta forma, uma fl y) ) = 0, 1111) 3, o qual corresponde ao seguinte número na base 10: fl y) = 0, , resultando em erros absoluto e relativo: EA y = 6, , E y = 5, = 5, 35%. Este procedimento de aproximação é denominado truncamento. 3 Uma definição mais rigorosa do método de truncamento será apresentada a seguir. Dado um número X já na forma normalizada que não possua representação exata no sistema x [b, n, e min, e max ]. Sejam agora X o maior número representável no sistema e que seja menor que X e X o menor número representável no sistema e que seja maior que X. Então, Pode-se escrever X como onde X X X. X = 0, d 1 d... d n ) b e + g X b e n, 0 g x < 1 é a parcela de X que não pode ser incluída na sua representação. Existem então maneiras de se realizar a aproximação: Truncamento. O truncamento consiste em simplesmente ignorar g X. Assim, fl X) = 0, d 1 d... d n ) b e, o qual é representável no sistema. Neste caso, os erros absoluto e relativo são EA X = X fl X) = g X b e n < b e n, E X = EA X fl X) = g X b e n 0, d 1 d... d n ) b e < b n = b n+1, 0, 1) b pois 0, d 1 d... d n ) 0, 1) b = b 1. Desta forma, obtém-se limites superiores para ambos os erros. No exemplo acima, pode-se escrever: y) = 0, 1111) 3 + g y 3 4, sendo g y = 0, ealizando então o truncamento, obtém-se fl y) ). Arredondamento. No arredondamento, 4 executa-se a seguinte operação: { 0, d 1 d... d n ) b e, se g X < 1 fl X) = 0, d 1 d... d n + 1)) b e, se g X ) Neste caso, o erro absoluto da operação será { g X b e n, se g X < 1 EA X = X fl X) = g X 1 b e n, se g X 1 < 1 be n ), 3 Tradução livre do termo em inglês chopping. 4 Tradução livre do termo inglês rounding. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
22 Erros na representação e na álgebra de ponto flutuante de onde se obtém uma estimativa superior e o erro relativo será 1 be n 0, d E X < 1 d... d n ) b e, se g X < 1 1 be n 0, d 1 d... d n + 1)) b e, se g X 1 < 1 be n 0, 1) b b e = 1 ) b n+1, o qual fornece uma estimativa superior para o erro relativo. No exemplo acima, como g y > 1/, deve-se somar 1 ao dígito d 4 resultando, com o auxílio da tabela de adição de binários apresentada na seção 1.3.1, fl y) ) = 0, 1111) 3 + 0, 0001) 3 = 1, 0000) 3 = 0, 1000). Neste caso, obtém-se fl y) = 0, 15, o qual possui um erro relativo de 1,% de y, bem menor que o erro obtido com o truncamento, que foi de 5,35%. Computadores mais recentes modificam ligeiramente o arredondamento em relação à fórmula apresentada em 1.6). Nesta, o último dígito significativo d n ) não será alterado se g X < 1/ e este será alterado se g X 1/. Há, portanto, uma ligeira preferência para a alteração de d n no processo de arredondamento, o que insere um erro sistemático no processo. Atualmente, se g X = 1/, o valor de d n será alterado somente em metade das situações, com base em algum critério. Este critério pode ser a paridade de d n, por exemplo. Assim, para b = 10 o número 1,5 seria arredondado para 1, enquanto que 13,5 seria arredondado para 14. Este critério é também denominado arredondamento par [6] Número de dígitos significativos Quando se conta o número de dígitos em um valor numérico, não se deve incluir os zeros no início do número, uma vez que estes zeros somente auxiliam a localizar a posição ideal do ponto decimal. Caso se queira contar o número de decimais, então os zeros à direita do ponto decimal devem ser incluídos. Por exemplo, o número 0, é dado com três dígitos mas possui cinco decimais. O número 1, 34 é dado com quatro dígitos, mas possui apenas dois decimais. Quando se trabalha com uma representação de um número obtida por meio de um processo de arredondamento ou truncamento, uma maneira alternativa para se estimar a qualidade da aproximação, ou seja a acurácia do número, consiste em computar o número de dígitos significativos corretos da representação. Se fl X) é uma aproximação de X com k dígitos significativos corretos em uma representação de base b, então X fl X) X = ɛ X 1 b k+1, onde k é o maior número inteiro positivo para o qual a inegualdade acima é verificada. Exemplo Sejam b = 10, X = 1/6 e fl X) = 0, 16667; então ɛ X = 1/6 0, /6 = Ou seja, o número de dígitos significativos em fl X) é k = Erros na álgebra de ponto flutuante Adicionalmente aos erros resultantes do truncamento ou do arredondamento na representação de números de ponto flutuante por computadores, as operações algébricas que necessariamente são realizadas pelo computador introduzem dois outros tipos de erros no resultado destas operações e que tendem a se acumular à medida que o número de operações de ponto flutuante são realizadas pelo computador. Estes erros são os erros de arredondamento 5 e os erros de truncamento. 6 Estes tipos de erros adicionais serão brevemente discutidos nesta seção. 5 Neste caso, o termo erros de arredondamento possui um significado distinto do processo de arredondamento utilizado na representação de números reais, discutida na seção O termo, neste contexto, consiste na tradução usualmente empregada para o termo em inglês round-off errors. 6 Aqui também, o termo erros de truncamento não se refere ao processo de truncamento discutido na seção 1.5.3, mas sim ao tipo de erro que em inglês é denominado truncation errors. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
23 Erros de arredondamento Capítulo 1. epresentação de Números e Erros 17 A origem deste tipo de erro está também relacionada com a representação finita das palavras em um computador e surge com a realização de operações de ponto flutuante pelo mesmo. Um exemplo simples ilustra o surgimento deste tipo de erro. Suponha-se que se esteja usando um sistema numérico de base 10 com 5 dígitos na mantissa, semelhante à representação 1.4). Deseja-se agora calcular o valor da função fx) = 1 cos x sen x = sen x 1 + cos x para x = 0, 007. otinas intrínsecas fornecidas pelo fabricante do compilador utilizado encarregam-se de calcular o valor das funções trigonométricas dentro da precisão disponível, por meio de um processo de arredondamento. Assim, A primeira expressão para fx) fornece: fx) = 1 cos x sen x enquanto que a segunda expressão fornece: fx) = = sen0, 007) = 0, cos0, 007) = 0, , , 10 4 = 0, , = 0, , sen x 0, = = 0, , 1 + cos x 1 + 0, sendo que este último resultado é o correto, dentro da precisão de 5 dígitos disponível. O erro relativo entre o primeiro valor errado) e o segundo correto) é de,5%. Na primeira expressão, devido à escolha feita na precisão, restou somente um dígito relevante no numerador após a subtração. Isto levou a uma perda de precisão e a um resultado errôneo devido ao cancelamento de dois números muito próximos entre si. Este problema seria evitado caso o sistema de representação dispusesse de, pelo menos, mais um dígito significativo na mantissa; porém, o ponto a ser frisado aqui é que muito facilmente este tipo de erro de arredondamento ocorre, devido ao tamanho finito da palavra no computador. Por outro lado, caso fosse solicitado o valor de fx) para x π, seria a segunda expressão que forneceria um valor incorreto, enquanto que a primeira forneceria um valor correto. Este exemplo simples demonstra a perda de precisão numérica devida a erros de arredondamento, onde o número de dígitos significativos é reduzido na subtração de dois números próximos entre si. Isto mostra que não é possível confiar cegamente no cálculo realizado; deve-se sempre analisar cuidadosamente o algoritmo empregado na procura de possíveis fontes de erros. Considera-se então um número real X, o qual possui uma representação de máquina fl X), que pode ser escrita como fl X) = X 1 + ɛ X ), onde ɛ X é o erro associado com a representação de X. De forma equivalente, pode-se escrever fl X) = X + δ X, sendo δ X = Xɛ X. Então, δ X = EA X. Pode-se ver que fl X) X ɛ X = = X fl X) X ɛ X = 1 + δ X fl X) fl X) + ɛ X = fl X) X fl X) fl X) X 1 fl X) fl X) X fl X) X = fl X) δ X fl X) ) δ X fl X) +... ) 1 X fl X) 1 1 δ X /fl X), fl X) X 1 + X fl X) fl X) ɛ X fl X) X fl X) X + fl X) fl X) ), ) X fl X), ou seja, ɛ X E X ɛ max, onde ɛ max é denominado de unidade na última posição 7, ou uup. Isto é, com k dígitos na mantissa e com a base b, uup b k. 7 Do termo em inglês unit in the last place, ou ulp. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
24 Erros na representação e na álgebra de ponto flutuante Dados agora dois números reais positivos X e Y, deseja-se estimar os erros relativos das operações algébricas entre ambos: X op Y, sendo op um das operações: +,, ou, conhecendo-se os erros relativos ɛ X e ɛ Y correspondentes: fl X) = X 1 + ɛ X ) e fl Y ) = Y 1 + ɛ Y ). Os resultados destas operações de ponto flutuante são escritos: fl X + Y ), fl X Y ), fl X Y ), fl X/Y ). Assumindo que não ocorra overflow nem underflow, supõe-se que seja possível escrever sendo fl X op Y ) = X op Y ) 1 + ɛ op ), ɛ op = fl X op Y ) X op Y ), X op Y ) com ɛ op = E op, o erro relativo da operação. Grande parte dos computadores atualmente empregados utilizam o padrão IEEE para operações aritméticas de ponto flutuante no sistema binário. Entre outros recursos, este padrão especifica que todas as operações aritméticas devem ser idealmente realizadas como se o computador dispusesse de precisão infinita e somente após obtido o resultado este deve ser transformado para o sistema de ponto flutuante em uso através de um processo de arredondamento [6]. Este procedimento pode ser implementado fazendo-se uso de dígitos de guarda guard digits) [6] e ele permite estimar o erro em cada operação de ponto flutuante como ɛ op max ɛ X, ɛ Y ). Desta forma, obtém-se o menor erro relativo possível na operação algébrica e este irá se propagar lentamente com o aumento do número de operações. Grande parte dos computadores em uso atualmente seguem o padrão IEEE, o qual exige o emprego dos dígitos de guarda. Caso este padrão não seja empregado, os erros decorrentes de operações de ponto flutuante aumentam de forma extremamente rápida com o número de operações. Neste último caso, para cada operação algébrica, obtém-se: Adição. esulta: fl X + Y ) = fl X) + fl Y ) = X + Y ) + δ X + δ Y ), a qual pode ser escrita: fl X + Y ) = X + Y ) 1 + δ ) X + δ Y = X + Y ) 1 + Xɛ ) X + Y ɛ Y X + Y ) 1 + ɛ + ), X + Y X + Y sendo ɛ + δ X + δ Y fl X) + fl Y ). Ou seja, os erros absoluto e relativo do processo de soma de ponto flutuante são: EA + = δ X + δ Y fl X) ɛ X + fl Y ) ɛ Y, E + = ɛ + = δ X + δ Y fl X) + fl Y ) = ɛ X 1 + fl Y ) /fl X) + ɛ Y 1 + fl X) /fl Y ). Há três situações possíveis na última expressão acima: 1. flx) fl Y ). Neste caso, obtém-se E + ɛ X.. fl X) fl Y ). Neste caso, E + ɛ Y. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
25 3. O [fl X)] = O [fl Y )]. 8 Agora, Capítulo 1. epresentação de Números e Erros 19 Conclui-se, portanto, que E + O [max ɛ X, ɛ Y )]. Subtração. De forma similar ao caso anterior, resulta: a qual pode ser escrita: sendo fl X Y ) = X Y ) E + 1 ɛ X + ɛ Y. fl X Y ) = fl X) fl Y ) = X Y ) + δ X δ Y ), 1 + δ ) X δ Y = X Y ) 1 + Xɛ ) X Y ɛ Y X Y ) 1 + ɛ ), X Y X Y ɛ δ X δ Y fl X) fl Y ). Ou seja, os erros absoluto e relativo do processo de soma de ponto flutuante são: EA = δ X δ Y = fl X) ɛ X fl Y ) ɛ Y, E = ɛ = δ X δ Y fl X) fl Y ) = ɛ X 1 fl Y ) /fl X) + ɛ Y 1 fl X) /fl Y ). Considerando os mesmos casos anteriores, 1. fl X) fl Y ). Neste caso,. fl X) fl Y ). Neste caso, E ɛ X. E ɛ Y. 3. O [fl X)] = O [fl Y )]. Agora, 1 fl Y ) /fl X) 1 e 1 fl X) /fl Y ) 1, resultando E ɛ X + ɛ Y. Este resultado mostra claramente como o erro relativo pode se tornar muito grande quando X Y. Isto ocorre porque a subtração de dois números muito próximos entre si resulta em um número cuja representação ocorre nos últimos dígitos da mantissa, resultando em um grande erro de arredondamento. Multiplicação. Neste caso, fl X Y ) = fl X) fl Y ) = X + δ X ) Y + δ Y ) = X Y + X δ Y + Y δ X + δ X δ Y. Supondo que δ X δ Y fl X) δ Y, fl Y ) δ X ), obtém-se fl X Y ) X Y ) + fl X) δ Y + fl Y ) δ X ). Por outro lado, fl X Y ) X Y ) 1 + fl X) δ Y + fl Y ) δ X = X Y ) 1 + δ X fl X) + fl X) fl Y ) δ ) Y X Y ) 1 + ɛ ). fl Y ) ) Assim, EA = fl X) δ Y + fl Y ) δ X, E = ɛ = δ X fl X) + δ Y fl Y ) ɛ X + ɛ Y. Portanto, E O [max ɛ X, ɛ Y )], da mesma forma que a adição. 8 A notação Ox) indica a ordem de grandeza de x. Uma definição rigorosa é apresentada na página. Autor: udi Gaelzer IFM/UFPel Versão: de julho de 009
Universidade Federal de São João Del Rei - UFSJ
 Universidade Federal de São João Del Rei - UFSJ Instituída pela Lei 0.45, de 9/04/00 - D.O.U. de /04/00 Pró-Reitoria de Ensino de Graduação - PROEN Disciplina: Cálculo Numérico Ano: 03 Prof: Natã Goulart
Universidade Federal de São João Del Rei - UFSJ Instituída pela Lei 0.45, de 9/04/00 - D.O.U. de /04/00 Pró-Reitoria de Ensino de Graduação - PROEN Disciplina: Cálculo Numérico Ano: 03 Prof: Natã Goulart
Aritmética de Ponto Flutuante e Noções de Erro. Ana Paula
 Aritmética de Ponto Flutuante e Noções de Erro Sumário 1 Introdução 2 Sistemas de Numeração 3 Representação de Números Inteiros no Computador 4 Representação de Números Reais no Computador 5 Operações
Aritmética de Ponto Flutuante e Noções de Erro Sumário 1 Introdução 2 Sistemas de Numeração 3 Representação de Números Inteiros no Computador 4 Representação de Números Reais no Computador 5 Operações
Representação de números em máquinas
 Capítulo 1 Representação de números em máquinas 1.1. Sistema de numeração Um sistema de numeração é formado por uma coleção de símbolos e regras para representar conjuntos de números de maneira consistente.
Capítulo 1 Representação de números em máquinas 1.1. Sistema de numeração Um sistema de numeração é formado por uma coleção de símbolos e regras para representar conjuntos de números de maneira consistente.
Notas de Cálculo Numérico
 Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Capítulo SETE Números em Ponto Fixo e Ponto Flutuante
 Capítulo SETE Números em Ponto Fixo e Ponto Flutuante 7.1 Números em ponto fixo Observação inicial: os termos ponto fixo e ponto flutuante são traduções diretas dos termos ingleses fixed point e floating
Capítulo SETE Números em Ponto Fixo e Ponto Flutuante 7.1 Números em ponto fixo Observação inicial: os termos ponto fixo e ponto flutuante são traduções diretas dos termos ingleses fixed point e floating
Análise de Arredondamento em Ponto Flutuante
 Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
Aritmética de Ponto Flutuante
 Aritmética de Ponto Flutuante Entre 1970 e 1980 um grupo formado por cientistas e engenheiros de diferentes empresas de computação realizou um trabalho intenso na tentativa de encontrar um padrão de representação
Aritmética de Ponto Flutuante Entre 1970 e 1980 um grupo formado por cientistas e engenheiros de diferentes empresas de computação realizou um trabalho intenso na tentativa de encontrar um padrão de representação
CCI-22 CCI-22. 2) Erros de arredondamento. Matemática Computacional
 Matemática Computacional 2) Erros de arredondamento Carlos Alberto Alonso Sanches Erros de representação e de cálculo Tipos de erros Erro inerente: sempre presente na incerteza das medidas experimentais
Matemática Computacional 2) Erros de arredondamento Carlos Alberto Alonso Sanches Erros de representação e de cálculo Tipos de erros Erro inerente: sempre presente na incerteza das medidas experimentais
Introdução. A Informação e sua Representação (Parte III) Universidade Federal de Campina Grande Departamento de Sistemas e Computação
 Universidade Federal de Campina Grande Departamento de Sistemas e Computação Introdução à Computação A Informação e sua Representação (Parte III) Prof.a Joseana Macêdo Fechine Régis de Araújo joseana@computacao.ufcg.edu.br
Universidade Federal de Campina Grande Departamento de Sistemas e Computação Introdução à Computação A Informação e sua Representação (Parte III) Prof.a Joseana Macêdo Fechine Régis de Araújo joseana@computacao.ufcg.edu.br
Introdução. A Informação e sua Representação (Parte II) Universidade Federal de Campina Grande. Unidade Acadêmica de Sistemas e Computação
 Universidade Federal de Campina Grande Unidade Acadêmica de Sistemas e Computação Introdução à Computação A Informação e sua Representação (Parte II) Prof. a Joseana Macêdo Fechine Régis de Araújo joseana@computacao.ufcg.edu.br
Universidade Federal de Campina Grande Unidade Acadêmica de Sistemas e Computação Introdução à Computação A Informação e sua Representação (Parte II) Prof. a Joseana Macêdo Fechine Régis de Araújo joseana@computacao.ufcg.edu.br
Índice de conteúdos. Índice de conteúdos. Capítulo 2. Representação de Números e Erros...1. 1.Representação de números em diferentes bases...
 Índice de conteúdos Índice de conteúdos Capítulo 2. Representação de Números e Erros...1 1.Representação de números em diferentes bases...1 1.1.Representação de números inteiros e conversões de base...1
Índice de conteúdos Índice de conteúdos Capítulo 2. Representação de Números e Erros...1 1.Representação de números em diferentes bases...1 1.1.Representação de números inteiros e conversões de base...1
Aula 2 Sistemas de Numeração (Revisão)
 Aula 2 Sistemas de Numeração (Revisão) Anderson L. S. Moreira anderson.moreira@recife.ifpe.edu.br http://dase.ifpe.edu.br/~alsm 1 O que fazer com essa apresentação 2 Agenda Breve revisão da aula anterior
Aula 2 Sistemas de Numeração (Revisão) Anderson L. S. Moreira anderson.moreira@recife.ifpe.edu.br http://dase.ifpe.edu.br/~alsm 1 O que fazer com essa apresentação 2 Agenda Breve revisão da aula anterior
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade
 REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
Eduardo Camponogara. DAS-5103: Cálculo Numérico para Controle e Automação. Departamento de Automação e Sistemas Universidade Federal de Santa Catarina
 Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle e Automação 1/48 Sumário Arredondamentos Erros 2/48 Sumário Arredondamentos
Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle e Automação 1/48 Sumário Arredondamentos Erros 2/48 Sumário Arredondamentos
Aula 2 - Cálculo Numérico
 Aula 2 - Cálculo Numérico Erros Prof. Phelipe Fabres Anhanguera Prof. Phelipe Fabres (Anhanguera) Aula 2 - Cálculo Numérico 1 / 41 Sumário Sumário 1 Sumário 2 Erros Modelagem Truncamento Representação
Aula 2 - Cálculo Numérico Erros Prof. Phelipe Fabres Anhanguera Prof. Phelipe Fabres (Anhanguera) Aula 2 - Cálculo Numérico 1 / 41 Sumário Sumário 1 Sumário 2 Erros Modelagem Truncamento Representação
As fases na resolução de um problema real podem, de modo geral, ser colocadas na seguinte ordem:
 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Introdução O Cálculo Numérico
1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Introdução O Cálculo Numérico
Cálculo Numérico Aula 1: Computação numérica. Tipos de Erros. Aritmética de ponto flutuante
 Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Organização e Arquitetura de Computadores I
 Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
CAPÍTULO I. UNIVERSIDADE FEDERAL DE UBERLÂNDIA FACULDADE DE ENGENHARIA ELÉTRICA Apostila de Eletrônica Digital. Sistemas de Numeração. 1.
 CAPÍTULO I Sistemas de Numeração. Introdução O decimal é o mais importante dos sistemas numéricos. Ele está fundamentado em certas regras que são a base de formação para qualquer outro sistema. Além do
CAPÍTULO I Sistemas de Numeração. Introdução O decimal é o mais importante dos sistemas numéricos. Ele está fundamentado em certas regras que são a base de formação para qualquer outro sistema. Além do
computador-cálculo numérico perfeita. As fases na resolução de um problema real podem, de modo geral, ser colocadas na seguinte ordem:
 1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
Capítulo 2. VARIÁVEIS DO TIPO INTEIRO
 Capítulo 2. VARIÁVEIS DO TIPO INTEIRO OBJETIVOS DO CAPÍTULO Conceitos de: variáveis do tipo inteiro, atribuição, avisos e erros de compilação, erros de execução, comentários dentro do programa-fonte Operadores
Capítulo 2. VARIÁVEIS DO TIPO INTEIRO OBJETIVOS DO CAPÍTULO Conceitos de: variáveis do tipo inteiro, atribuição, avisos e erros de compilação, erros de execução, comentários dentro do programa-fonte Operadores
Unidade 5: Sistemas de Representação
 Arquitetura e Organização de Computadores Atualização: 9/8/ Unidade 5: Sistemas de Representação Números de Ponto Flutuante IEEE 754/8 e Caracteres ASCII Prof. Daniel Caetano Objetivo: Compreender a representação
Arquitetura e Organização de Computadores Atualização: 9/8/ Unidade 5: Sistemas de Representação Números de Ponto Flutuante IEEE 754/8 e Caracteres ASCII Prof. Daniel Caetano Objetivo: Compreender a representação
Capítulo 1 - Erros e Aritmética Computacional
 Capítulo 1 - Erros e Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança 2 o Ano - Eng. Civil, Electrotécnica e Mecânica Carlos Balsa Métodos Numéricos
Capítulo 1 - Erros e Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança 2 o Ano - Eng. Civil, Electrotécnica e Mecânica Carlos Balsa Métodos Numéricos
A declaração de uma variável vel define o seu tipo. O tipo do dado define como ele será: Armazenado na memória. Manipulado pela ULA.
 Representação de Dados Tipos de dados: Caracteres (letras, números n e símbolos). s Lógicos. Inteiros. Ponto flutuante: Notações decimais: BCD. A declaração de uma variável vel define o seu tipo. O tipo
Representação de Dados Tipos de dados: Caracteres (letras, números n e símbolos). s Lógicos. Inteiros. Ponto flutuante: Notações decimais: BCD. A declaração de uma variável vel define o seu tipo. O tipo
Noções Básicas de Erros
 Noções Básicas de Erros PROF. ALIRIO SANTOS DE SÁ ALIRIOSA@UFBA.BR MATERIAL ADAPTADA DOS SLIDES DA DISCIPLINA DE CÁLCULO NUMÉRICO DOS PROFESSORES BRUNO QUEIROZ, JOSÉ QUEIROZ E MARCELO BARROS (UFCG). DISPONÍVEL
Noções Básicas de Erros PROF. ALIRIO SANTOS DE SÁ ALIRIOSA@UFBA.BR MATERIAL ADAPTADA DOS SLIDES DA DISCIPLINA DE CÁLCULO NUMÉRICO DOS PROFESSORES BRUNO QUEIROZ, JOSÉ QUEIROZ E MARCELO BARROS (UFCG). DISPONÍVEL
Algoritmos DCC 119. Introdução e Conceitos Básicos
 Algoritmos DCC 119 Introdução e Conceitos Básicos Sumário Sistemas de Numeração Sistemas Computacionais Estrutura de um Computador Digital Sistemas Operacionais Algoritmo Introdução Formas de representação
Algoritmos DCC 119 Introdução e Conceitos Básicos Sumário Sistemas de Numeração Sistemas Computacionais Estrutura de um Computador Digital Sistemas Operacionais Algoritmo Introdução Formas de representação
Equações Diferenciais Ordinárias
 Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
TEXTO DE REVISÃO: Uso da calculadora científica e potências de 10.
 TEXTO DE REVISÃO: Uso da calculadora científica e potências de 10. Caro aluno (a): No livro texto (Halliday) cap.01 - Medidas alguns conceitos muito importantes são apresentados. Por exemplo, é muito importante
TEXTO DE REVISÃO: Uso da calculadora científica e potências de 10. Caro aluno (a): No livro texto (Halliday) cap.01 - Medidas alguns conceitos muito importantes são apresentados. Por exemplo, é muito importante
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Estudaremos métodos numéricos para resolução de sistemas lineares com n equações e n incógnitas. Estes podem ser:
 1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
ANÁLISE NUMÉRICA DEC - 1996/97
 ANÁLISE NUMÉRICA DEC - 996/97 Teoria de Erros A Teoria de Erros fornece técnicas para quantificar erros nos dados e nos resultados de cálculos com números aproximados. Nos cálculos aproximados deve-se
ANÁLISE NUMÉRICA DEC - 996/97 Teoria de Erros A Teoria de Erros fornece técnicas para quantificar erros nos dados e nos resultados de cálculos com números aproximados. Nos cálculos aproximados deve-se
Representando Instruções no Computador
 Representando Instruções no Computador Humanos aprenderam a pensar na base 10 Números podem ser representados em qualquer base Números mantidos no hardware como série de sinais eletrônicos altos e baixos
Representando Instruções no Computador Humanos aprenderam a pensar na base 10 Números podem ser representados em qualquer base Números mantidos no hardware como série de sinais eletrônicos altos e baixos
Métodos Numéricos. Turma CI-202-X. Josiney de Souza. josineys@inf.ufpr.br
 Métodos Numéricos Turma CI-202-X Josiney de Souza josineys@inf.ufpr.br Agenda do Dia Aula 3 (10/08/15) Aritmética de ponto flutuante Representação de ponto flutuante Normalização Binária Decimal Situações
Métodos Numéricos Turma CI-202-X Josiney de Souza josineys@inf.ufpr.br Agenda do Dia Aula 3 (10/08/15) Aritmética de ponto flutuante Representação de ponto flutuante Normalização Binária Decimal Situações
Sistemas de Numeração
 Sistemas de Numeração Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes Sistemas de Numeração Prover símbolos e convenções
Sistemas de Numeração Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes Sistemas de Numeração Prover símbolos e convenções
Resolução de sistemas lineares
 Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Noções Básicas Sobre Erros
 Noções Básicas Sobre Erros Wellington D. Previero previero@utfpr.edu.br http://paginapessoal.utfpr.edu.br/previero Universidade Tecnológica Federal do Paraná - UTFPR Câmpus Londrina Wellington D. Previero
Noções Básicas Sobre Erros Wellington D. Previero previero@utfpr.edu.br http://paginapessoal.utfpr.edu.br/previero Universidade Tecnológica Federal do Paraná - UTFPR Câmpus Londrina Wellington D. Previero
2. Representação Numérica
 2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE. Prof. Dr. Daniel Caetano 2012-1
 ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE Prof. Dr. Daniel Caetano 2012-1 Objetivos Compreender o que é notação em ponto flutuante Compreender a
ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE Prof. Dr. Daniel Caetano 2012-1 Objetivos Compreender o que é notação em ponto flutuante Compreender a
Sistemas de Numeração (Aula Extra)
 Sistemas de Numeração (Aula Extra) Sistemas de diferentes bases Álgebra Booleana Roberta Lima Gomes - LPRM/DI/UFES Sistemas de Programação I Eng. Elétrica 27/2 Sistemas de Numeração Um sistema de numeração
Sistemas de Numeração (Aula Extra) Sistemas de diferentes bases Álgebra Booleana Roberta Lima Gomes - LPRM/DI/UFES Sistemas de Programação I Eng. Elétrica 27/2 Sistemas de Numeração Um sistema de numeração
Introdução à Física Computacional
 Introdução à Física Computacional Apostila preparada para a disciplina de Modelos Computacionais da Física I, ministrada para o Curso de Licenciatura em Física do Departamento de Física, Instituto de Física
Introdução à Física Computacional Apostila preparada para a disciplina de Modelos Computacionais da Física I, ministrada para o Curso de Licenciatura em Física do Departamento de Física, Instituto de Física
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Capítulo 8. CICLOS. Tabela 8.1 Programa8a.f90.
 Capítulo 8. CICLOS OBJETIVOS DO CAPÍTULO Conceito de ciclo Comandos do FORTRAN: DO END DO, EXIT 8.1 programa8a.f90 Para inicializar as atividades deste capítulo, deve-se executar: 1) Para acessar o programa
Capítulo 8. CICLOS OBJETIVOS DO CAPÍTULO Conceito de ciclo Comandos do FORTRAN: DO END DO, EXIT 8.1 programa8a.f90 Para inicializar as atividades deste capítulo, deve-se executar: 1) Para acessar o programa
INSTITUTO TECNOLÓGICO
 PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
Principais códigos utilizados. Codificação. Código binário puro. Codificação binária. Codificação Binária. Código Binário puro e suas variantes
 Codificação Principais códigos utilizados Computadores e Equipamentos de Comunicações Digitais trabalham com representação e códigos. A codificação binária de sinais é largamente utilizada em Sistemas
Codificação Principais códigos utilizados Computadores e Equipamentos de Comunicações Digitais trabalham com representação e códigos. A codificação binária de sinais é largamente utilizada em Sistemas
Capítulo 1. Introdução. 1.1 Sistemas numéricos
 EQE-358 MÉTODOS NUMÉRICOS EM ENGENHARIA QUÍMICA PROFS. EVARISTO E ARGIMIRO Capítulo 1 Introdução O objetivo desta disciplina é discutir e aplicar técnicas e métodos numéricos para a resolução de problemas
EQE-358 MÉTODOS NUMÉRICOS EM ENGENHARIA QUÍMICA PROFS. EVARISTO E ARGIMIRO Capítulo 1 Introdução O objetivo desta disciplina é discutir e aplicar técnicas e métodos numéricos para a resolução de problemas
Álgebra. SeM MiSTéRio
 Álgebra SeM MiSTéRio Série SeM MiSTéRio Alemão Sem Mistério Álgebra Sem Mistério Cálculo Sem Mistério Conversação em Alemão Sem Mistério Conversação em Espanhol Sem Mistério Conversação em Francês Sem
Álgebra SeM MiSTéRio Série SeM MiSTéRio Alemão Sem Mistério Álgebra Sem Mistério Cálculo Sem Mistério Conversação em Alemão Sem Mistério Conversação em Espanhol Sem Mistério Conversação em Francês Sem
Fração como porcentagem. Sexto Ano do Ensino Fundamental. Autor: Prof. Francisco Bruno Holanda Revisor: Prof. Antonio Caminha M.
 Material Teórico - Módulo de FRAÇÕES COMO PORCENTAGEM E PROBABILIDADE Fração como porcentagem Sexto Ano do Ensino Fundamental Autor: Prof. Francisco Bruno Holanda Revisor: Prof. Antonio Caminha M. Neto
Material Teórico - Módulo de FRAÇÕES COMO PORCENTAGEM E PROBABILIDADE Fração como porcentagem Sexto Ano do Ensino Fundamental Autor: Prof. Francisco Bruno Holanda Revisor: Prof. Antonio Caminha M. Neto
7 - Análise de redes Pesquisa Operacional CAPÍTULO 7 ANÁLISE DE REDES. 4 c. Figura 7.1 - Exemplo de um grafo linear.
 CAPÍTULO 7 7 ANÁLISE DE REDES 7.1 Conceitos Básicos em Teoria dos Grafos Diversos problemas de programação linear, inclusive os problemas de transporte, podem ser modelados como problemas de fluxo de redes.
CAPÍTULO 7 7 ANÁLISE DE REDES 7.1 Conceitos Básicos em Teoria dos Grafos Diversos problemas de programação linear, inclusive os problemas de transporte, podem ser modelados como problemas de fluxo de redes.
Cálculo Numérico / Métodos Numéricos. Representação de números em computadores Mudança de base 14:05
 Cálculo Numérico / Métodos Numéricos Representação de números em computadores Mudança de base 14:05 Computadores são "binários" Por que 0 ou 1? 0 ou 1 - "fácil" de obter um sistema físico Transistores
Cálculo Numérico / Métodos Numéricos Representação de números em computadores Mudança de base 14:05 Computadores são "binários" Por que 0 ou 1? 0 ou 1 - "fácil" de obter um sistema físico Transistores
O ENSINO DE CÁLCULO NUMÉRICO: UMA EXPERIÊNCIA COM ALUNOS DO CURSO DE CIÊNCIA DA COMPUTAÇÃO
 O ENSINO DE CÁLCULO NUMÉRICO: UMA EXPERIÊNCIA COM ALUNOS DO CURSO DE CIÊNCIA DA COMPUTAÇÃO Prof. Leugim Corteze Romio Universidade Regional Integrada URI Campus Santiago-RS leugimcr@urisantiago.br Prof.
O ENSINO DE CÁLCULO NUMÉRICO: UMA EXPERIÊNCIA COM ALUNOS DO CURSO DE CIÊNCIA DA COMPUTAÇÃO Prof. Leugim Corteze Romio Universidade Regional Integrada URI Campus Santiago-RS leugimcr@urisantiago.br Prof.
Representação de Dados
 Representação de Dados Introdução Todos sabemos que existem diferentes tipos de números: fraccionários, inteiros positivos e negativos, etc. Torna-se necessária a representação destes dados em sistema
Representação de Dados Introdução Todos sabemos que existem diferentes tipos de números: fraccionários, inteiros positivos e negativos, etc. Torna-se necessária a representação destes dados em sistema
Sistema de ponto flutuante
 Exemplo: FP(,4,,A) e FP(,4,,T) Sistema de ponto flutuante FP( b, p, q,_) = FP(, 4,, _ ) base 4 dígitos na mantissa dígitos no expoente A=Arredondamento T=Truncatura x ± =± m b t x =± d 1d d d 4 dígitos
Exemplo: FP(,4,,A) e FP(,4,,T) Sistema de ponto flutuante FP( b, p, q,_) = FP(, 4,, _ ) base 4 dígitos na mantissa dígitos no expoente A=Arredondamento T=Truncatura x ± =± m b t x =± d 1d d d 4 dígitos
Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara. Carga Horária: 60h
 Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara Carga Horária: 60h Representação de grandeza com sinal O bit mais significativo representa o sinal: 0 (indica um número
Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara Carga Horária: 60h Representação de grandeza com sinal O bit mais significativo representa o sinal: 0 (indica um número
Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto
 Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto Maria Angélica Araújo Universidade Federal de Uberlândia - Faculdade de Matemática Graduanda em Matemática - Programa de Educação
Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto Maria Angélica Araújo Universidade Federal de Uberlândia - Faculdade de Matemática Graduanda em Matemática - Programa de Educação
TRABALHANDO COM ARQUIVOS ENTRADAS/SAÍDAS (I/O) DE DADOS
 livrof90_v5 2007/3/1 10:27 page 41 #1 CAPÍTULO2 TRABALHANDO COM ARQUIVOS ENTRADAS/SAÍDAS (I/O) DE DADOS Neste capítulo você encontrará: 2.1 Introdução.................. 41 Arquivo................. 42 2.2
livrof90_v5 2007/3/1 10:27 page 41 #1 CAPÍTULO2 TRABALHANDO COM ARQUIVOS ENTRADAS/SAÍDAS (I/O) DE DADOS Neste capítulo você encontrará: 2.1 Introdução.................. 41 Arquivo................. 42 2.2
Como foi visto no tópico anterior, existem duas formas básicas para representar uma função lógica qualquer:
 ELETRÔNI IGITl I FUNÇÕES LÓGIS Formas de representação de uma função lógica omo foi visto no tópico anterior, existem duas formas básicas para representar uma função lógica qualquer: Soma de Produtos Produtos
ELETRÔNI IGITl I FUNÇÕES LÓGIS Formas de representação de uma função lógica omo foi visto no tópico anterior, existem duas formas básicas para representar uma função lógica qualquer: Soma de Produtos Produtos
aplicada a problemas de poluição do ar
 Biomatemática 17 (2007), 21 34 ISSN 1679-365X Uma Publicação do Grupo de Biomatemática IMECC UNICAMP Programação matemática fuzzy aplicada a problemas de poluição do ar Luiza A. Pinto Cantão 1, Depto.
Biomatemática 17 (2007), 21 34 ISSN 1679-365X Uma Publicação do Grupo de Biomatemática IMECC UNICAMP Programação matemática fuzzy aplicada a problemas de poluição do ar Luiza A. Pinto Cantão 1, Depto.
VIII. VARIÁVEIS. Tabela I ARQUITETURA DA MEMÓRIA. 0x0000 0x34 0x0001 0xB0 0x0002 0x23. 0xFFFF 0x00
 Fundamentos da Programação 32 A. Conceito Variáveis contém dados: VIII. VARIÁVEIS de entrada que o computador precisa manipular; de saída que o computador precisa imprimir; e temporários, utilizados de
Fundamentos da Programação 32 A. Conceito Variáveis contém dados: VIII. VARIÁVEIS de entrada que o computador precisa manipular; de saída que o computador precisa imprimir; e temporários, utilizados de
Notas sobre a Fórmula de Taylor e o estudo de extremos
 Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Problemas de Valor Inicial para Equações Diferenciais Ordinárias
 Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
3 - CONJUNTO DOS NÚMEROS RACIONAIS
 3 - CONJUNTO DOS NÚMEROS RACIONAIS Introdução É o conjunto de todos os números que estão ou podem ser colocados em forma de fração. Fração Quando dividimos um todo em partes iguais e queremos representar
3 - CONJUNTO DOS NÚMEROS RACIONAIS Introdução É o conjunto de todos os números que estão ou podem ser colocados em forma de fração. Fração Quando dividimos um todo em partes iguais e queremos representar
Programação: Tipos, Variáveis e Expressões
 Programação de Computadores I Aula 05 Programação: Tipos, Variáveis e Expressões José Romildo Malaquias Departamento de Computação Universidade Federal de Ouro Preto 2011-1 1/56 Valores Valor é uma entidade
Programação de Computadores I Aula 05 Programação: Tipos, Variáveis e Expressões José Romildo Malaquias Departamento de Computação Universidade Federal de Ouro Preto 2011-1 1/56 Valores Valor é uma entidade
Universidade Federal de São Carlos Departamento de Matemática 083020 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/04/2008
 Universidade Federal de São Carlos Departamento de Matemática 08300 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/0/008 1. (0 pts.) Considere o sistema de ponto flutuante normalizado
Universidade Federal de São Carlos Departamento de Matemática 08300 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/0/008 1. (0 pts.) Considere o sistema de ponto flutuante normalizado
CAPÍTULO 9. PROCESSAMENTO DOS DADOS 9.5. ALGARISMOS SIGNIFICATIVOS. =0.01 gcm 3 3.36 Logo o resultado experimental é: = 5.82 g 0.
 CAPÍTULO 9. PROCESSAMENTO DOS DADOS 9.5. ALGARISMOS SIGNIFICATIVOS Logo o resultado experimental é: =(1.732 ± 0.001) gcm 3 O erro relativo do volume (0.1%) é uma ordem de grandeza maior que o erro relativo
CAPÍTULO 9. PROCESSAMENTO DOS DADOS 9.5. ALGARISMOS SIGNIFICATIVOS Logo o resultado experimental é: =(1.732 ± 0.001) gcm 3 O erro relativo do volume (0.1%) é uma ordem de grandeza maior que o erro relativo
Organização e Arquitetura de Computadores. Aula 10 Ponto Flutuante Parte I. 2002 Juliana F. Camapum Wanderley
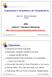 Organização e Arquitetura de Computadores Aula 10 Ponto Flutuante Parte I 2002 Juliana F. Camapum Wanderley http://www.cic.unb.br/docentes/juliana/cursos/oac OAC Ponto Flutuante Parte I - 1 Panorama Números
Organização e Arquitetura de Computadores Aula 10 Ponto Flutuante Parte I 2002 Juliana F. Camapum Wanderley http://www.cic.unb.br/docentes/juliana/cursos/oac OAC Ponto Flutuante Parte I - 1 Panorama Números
CURSO de CIÊNCIA DA COMPUTAÇÃO - Gabarito
 UNIVERSIDADE FEDERAL FLUMINENSE TRANSFERÊNCIA 2 o semestre letivo de 2005 e 1 o semestre letivo de 2006 CURSO de CIÊNCIA DA COMPUTAÇÃO - Gabarito Verifique se este caderno contém : INSTRUÇÕES AO CANDIDATO
UNIVERSIDADE FEDERAL FLUMINENSE TRANSFERÊNCIA 2 o semestre letivo de 2005 e 1 o semestre letivo de 2006 CURSO de CIÊNCIA DA COMPUTAÇÃO - Gabarito Verifique se este caderno contém : INSTRUÇÕES AO CANDIDATO
Computador HIPO. Inicialmente vamos apresentar as unidades fundamentais de um computador:
 Computador HIPO Para introduzirmos as noções básicas de como funciona um computador, empregaremos um modelo imaginário (hipotético) que denominaremos de computador hipo. O funcionamento desse modelo tem
Computador HIPO Para introduzirmos as noções básicas de como funciona um computador, empregaremos um modelo imaginário (hipotético) que denominaremos de computador hipo. O funcionamento desse modelo tem
DICAS PARA CÁLCULOS MAIS RÁPIDOS ARTIGO 06
 DICAS PARA CÁLCULOS MAIS RÁPIDOS ARTIGO 06 Este é o 6º artigo da série de dicas para facilitar / agilizar os cálculos matemáticos envolvidos em questões de Raciocínio Lógico, Matemática, Matemática Financeira
DICAS PARA CÁLCULOS MAIS RÁPIDOS ARTIGO 06 Este é o 6º artigo da série de dicas para facilitar / agilizar os cálculos matemáticos envolvidos em questões de Raciocínio Lógico, Matemática, Matemática Financeira
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) I Representação dos números, aritmética de ponto flutuante e erros em máquinas
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) I Representação dos números, aritmética de ponto flutuante e erros em máquinas
PLANIFICAÇÃO ANUAL MATEMÁTICA 3 DOMÍNIOS OBJETIVOS ATIVIDADES
 PLANIFICAÇÃO ANUAL MATEMÁTICA 3 DOMÍNIOS OBJETIVOS ATIVIDADES Números naturais Conhecer os numerais ordinais Utilizar corretamente os numerais ordinais até centésimo. Contar até um milhão Estender as regras
PLANIFICAÇÃO ANUAL MATEMÁTICA 3 DOMÍNIOS OBJETIVOS ATIVIDADES Números naturais Conhecer os numerais ordinais Utilizar corretamente os numerais ordinais até centésimo. Contar até um milhão Estender as regras
Karine Nayara F. Valle. Métodos Numéricos de Euler e Runge-Kutta
 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
Aula 1 Representação e Operações Aritméticas em Ponto Flutuante.
 Aula 1 Representação e Operações Aritméticas em Ponto Flutuante. MS211 - Cálculo Numérico Marcos Eduardo Valle Departamento de Matemática Aplicada Instituto de Matemática, Estatística e Computação Científica
Aula 1 Representação e Operações Aritméticas em Ponto Flutuante. MS211 - Cálculo Numérico Marcos Eduardo Valle Departamento de Matemática Aplicada Instituto de Matemática, Estatística e Computação Científica
CONCEITOS BÁSICOS PARA A CONSTRUÇÃO DE ALGORITMOS PARA COMPUTADORES. Isac Aguiar isacaguiar.com.br isacaguiar@gmail.com
 CONCEITOS BÁSICOS PARA A CONSTRUÇÃO DE ALGORITMOS PARA COMPUTADORES Isac Aguiar isacaguiar.com.br isacaguiar@gmail.com Objetivos Compreender os conceitos de lógica de programação e de algoritmos. Conhecer
CONCEITOS BÁSICOS PARA A CONSTRUÇÃO DE ALGORITMOS PARA COMPUTADORES Isac Aguiar isacaguiar.com.br isacaguiar@gmail.com Objetivos Compreender os conceitos de lógica de programação e de algoritmos. Conhecer
Aula 3 - Sistemas de Numeração
 UEM Universidade Estadual de Maringá DIN - Departamento de Informática Disciplina: Fundamentos da Computação Profª Thelma Elita Colanzi Lopes thelma@din.uem.br Aula 3 - Sistemas de Numeração O ser humano,
UEM Universidade Estadual de Maringá DIN - Departamento de Informática Disciplina: Fundamentos da Computação Profª Thelma Elita Colanzi Lopes thelma@din.uem.br Aula 3 - Sistemas de Numeração O ser humano,
x d z θ i Figura 2.1: Geometria das placas paralelas (Vista Superior).
 2 Lentes Metálicas Este capítulo destina-se a apresentar os princípios básicos de funcionamento e dimensionamento de lentes metálicas. Apresenta, ainda, comparações com as lentes dielétricas, cujas técnicas
2 Lentes Metálicas Este capítulo destina-se a apresentar os princípios básicos de funcionamento e dimensionamento de lentes metálicas. Apresenta, ainda, comparações com as lentes dielétricas, cujas técnicas
Primeiro roteiro de exercícios no Scilab Cálculo Numérico
 Primeiro roteiro de exercícios no Scilab Cálculo Numérico Rodrigo Fresneda 13 de fevereiro de 2012 Guia para respostas: Responda a todas as questões que estão em negrito ao longo do roteiro. Inclua sempre
Primeiro roteiro de exercícios no Scilab Cálculo Numérico Rodrigo Fresneda 13 de fevereiro de 2012 Guia para respostas: Responda a todas as questões que estão em negrito ao longo do roteiro. Inclua sempre
Frações. Números Racionais
 Frações Números Racionais Consideremos a operação 4:5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números porque não há
Frações Números Racionais Consideremos a operação 4:5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números porque não há
Escola Secundária c/3º CEB José Macedo Fragateiro. Curso Profissional de Nível Secundário. Componente Técnica. Disciplina de
 Escola Secundária c/3º CEB José Macedo Fragateiro Curso Profissional de Nível Secundário Componente Técnica Disciplina de Sistemas Digitais e Arquitectura de Computadores 29/21 Módulo 1: Sistemas de Numeração
Escola Secundária c/3º CEB José Macedo Fragateiro Curso Profissional de Nível Secundário Componente Técnica Disciplina de Sistemas Digitais e Arquitectura de Computadores 29/21 Módulo 1: Sistemas de Numeração
4. Tarefa 16 Introdução ao Ruído. Objetivo: Método: Capacitações: Módulo Necessário: Análise de PCM e de links 53-170
 4. Tarefa 16 Introdução ao Ruído Objetivo: Método: Ao final desta Tarefa você: Estará familiarizado com o conceito de ruído. Será capaz de descrever o efeito do Ruído em um sistema de comunicações digitais.
4. Tarefa 16 Introdução ao Ruído Objetivo: Método: Ao final desta Tarefa você: Estará familiarizado com o conceito de ruído. Será capaz de descrever o efeito do Ruído em um sistema de comunicações digitais.
TÉCNICAS DE PROGRAMAÇÃO
 TÉCNICAS DE PROGRAMAÇÃO (Adaptado do texto do prof. Adair Santa Catarina) ALGORITMOS COM QUALIDADE MÁXIMAS DE PROGRAMAÇÃO 1) Algoritmos devem ser feitos para serem lidos por seres humanos: Tenha em mente
TÉCNICAS DE PROGRAMAÇÃO (Adaptado do texto do prof. Adair Santa Catarina) ALGORITMOS COM QUALIDADE MÁXIMAS DE PROGRAMAÇÃO 1) Algoritmos devem ser feitos para serem lidos por seres humanos: Tenha em mente
Truques e Dicas. = 7 30 Para multiplicar fracções basta multiplicar os numeradores e os denominadores: 2 30 = 12 5
 Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Universidade Federal do Rio Grande do Norte. Centro De Ciências Exatas e da Terra. Departamento de Física Teórica e Experimental
 Universidade Federal do Rio Grande do Norte Centro De Ciências Exatas e da Terra Departamento de Física Teórica e Experimental Programa de Educação Tutorial Curso de Nivelamento: Pré-Cálculo PET DE FÍSICA:
Universidade Federal do Rio Grande do Norte Centro De Ciências Exatas e da Terra Departamento de Física Teórica e Experimental Programa de Educação Tutorial Curso de Nivelamento: Pré-Cálculo PET DE FÍSICA:
Circuitos Digitais 144L
 Circuitos Digitais Notas de Aula - 02 INSTITUTO: CURSO: DISCIPLINA: Instituto de Ciências Exatas e Tecnologia Ciência da Computação e Sistemas de Informação Circuitos Digitais 144L 1.0 Circuitos Combinacionais.
Circuitos Digitais Notas de Aula - 02 INSTITUTO: CURSO: DISCIPLINA: Instituto de Ciências Exatas e Tecnologia Ciência da Computação e Sistemas de Informação Circuitos Digitais 144L 1.0 Circuitos Combinacionais.
Notas da disciplina Cálculo Numérico
 Notas da disciplina Cálculo Numérico Leonardo F. Guidi 7 de outubro de 2015 Instituto de Matemática Universidade Federal do Rio Grande do Sul Av. Bento Gonçalves, 9500 Porto Alegre - RS 2 Sumário 1 Representação
Notas da disciplina Cálculo Numérico Leonardo F. Guidi 7 de outubro de 2015 Instituto de Matemática Universidade Federal do Rio Grande do Sul Av. Bento Gonçalves, 9500 Porto Alegre - RS 2 Sumário 1 Representação
Bem-vindo ao curso delta Gerenciamento de peso para a versão 9.1. Este curso aborda a nova solução de peso introduzida nessa versão.
 Bem-vindo ao curso delta Gerenciamento de peso para a versão 9.1. Este curso aborda a nova solução de peso introduzida nessa versão. Você deve ter bons conhecimentos de estoque, UM e administração de posições
Bem-vindo ao curso delta Gerenciamento de peso para a versão 9.1. Este curso aborda a nova solução de peso introduzida nessa versão. Você deve ter bons conhecimentos de estoque, UM e administração de posições
Este procedimento gera contribuições não só a φ 2 e φ 4, mas também a ordens superiores. O termo por exemplo:
 Teoria Quântica de Campos II 168 Este procedimento gera contribuições não só a φ 2 e φ 4, mas também a ordens superiores. O termo por exemplo: Obtemos acoplamentos com derivadas também. Para o diagrama
Teoria Quântica de Campos II 168 Este procedimento gera contribuições não só a φ 2 e φ 4, mas também a ordens superiores. O termo por exemplo: Obtemos acoplamentos com derivadas também. Para o diagrama
Algoritmos e Estruturas de Dados I 01/2013. Estruturas Condicionais e de Repetição (parte 2) Pedro O.S. Vaz de Melo
 Algoritmos e Estruturas de Dados I 01/2013 Estruturas Condicionais e de Repetição (parte 2) Pedro O.S. Vaz de Melo Problema 1 Suponha que soma (+) e subtração (-) são as únicas operações disponíveis em
Algoritmos e Estruturas de Dados I 01/2013 Estruturas Condicionais e de Repetição (parte 2) Pedro O.S. Vaz de Melo Problema 1 Suponha que soma (+) e subtração (-) são as únicas operações disponíveis em
Métodos Quantitativos Prof. Ms. Osmar Pastore e Prof. Ms. Francisco Merlo. Funções Exponenciais e Logarítmicas Progressões Matemáticas
 Métodos Quantitativos Prof. Ms. Osmar Pastore e Prof. Ms. Francisco Merlo Funções Exponenciais e Logarítmicas Progressões Matemáticas Funções Exponenciais e Logarítmicas. Progressões Matemáticas Objetivos
Métodos Quantitativos Prof. Ms. Osmar Pastore e Prof. Ms. Francisco Merlo Funções Exponenciais e Logarítmicas Progressões Matemáticas Funções Exponenciais e Logarítmicas. Progressões Matemáticas Objetivos
por séries de potências
 Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
3º Ano do Ensino Médio. Aula nº10 Prof. Daniel Szente
 Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº10 Prof. Daniel Szente Assunto: Função exponencial e logarítmica 1. Potenciação e suas propriedades Definição: Potenciação é a operação
Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº10 Prof. Daniel Szente Assunto: Função exponencial e logarítmica 1. Potenciação e suas propriedades Definição: Potenciação é a operação
ARQUITETURA DE COMPUTADORES. Sistemas de Numeração. 1 Arquitetura de Computadores
 ARQUITETURA DE COMPUTADORES Sistemas de Numeração 1 Sistemas de Numeração e Conversão de Base Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,3,4,5,6,7,8 e 9. Números superiores a 9; convencionamos
ARQUITETURA DE COMPUTADORES Sistemas de Numeração 1 Sistemas de Numeração e Conversão de Base Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,3,4,5,6,7,8 e 9. Números superiores a 9; convencionamos
Agrupamento de Escolas Eugénio de Castro 1º Ciclo. Critérios de Avaliação. Ano Letivo 2015/16 Disciplina MATEMÁTICA 3.º Ano
 Agrupamento de Escolas Eugénio de Castro 1º Ciclo Critérios de Avaliação Ano Letivo 2015/16 Disciplina MATEMÁTICA 3.º Ano Números e Operações Números naturais Utilizar corretamente os numerais ordinais
Agrupamento de Escolas Eugénio de Castro 1º Ciclo Critérios de Avaliação Ano Letivo 2015/16 Disciplina MATEMÁTICA 3.º Ano Números e Operações Números naturais Utilizar corretamente os numerais ordinais
Matemática Básica - 08. Função Logarítmica
 Matemática Básica Função Logarítmica 08 Versão: Provisória 0. Introdução Quando calculamos as equações exponenciais, o método usado consistia em reduzirmos os dois termos da equação à mesma base, como
Matemática Básica Função Logarítmica 08 Versão: Provisória 0. Introdução Quando calculamos as equações exponenciais, o método usado consistia em reduzirmos os dois termos da equação à mesma base, como
Exemplo de Subtração Binária
 Exemplo de Subtração Binária Exercícios Converta para binário e efetue as seguintes operações: a) 37 10 30 10 b) 83 10 82 10 c) 63 8 34 8 d) 77 8 11 8 e) BB 16 AA 16 f) C43 16 195 16 3.5.3 Divisão binária:
Exemplo de Subtração Binária Exercícios Converta para binário e efetue as seguintes operações: a) 37 10 30 10 b) 83 10 82 10 c) 63 8 34 8 d) 77 8 11 8 e) BB 16 AA 16 f) C43 16 195 16 3.5.3 Divisão binária:
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
Capítulo 13. VARIÁVEIS DO TIPO REAL DUPLA
 Capítulo 13. VARIÁVEIS DO TIPO REAL DUPLA OBJETIVOS DO CAPÍTULO Conceitos de: variáveis de precisão simples e dupla, variáveis do tipo real simples e dupla, mistura de variáveis do tipo inteiro com real
Capítulo 13. VARIÁVEIS DO TIPO REAL DUPLA OBJETIVOS DO CAPÍTULO Conceitos de: variáveis de precisão simples e dupla, variáveis do tipo real simples e dupla, mistura de variáveis do tipo inteiro com real
QUESTÕES COMENTADAS E RESOLVIDAS
 LENIMAR NUNES DE ANDRADE INTRODUÇÃO À ÁLGEBRA: QUESTÕES COMENTADAS E RESOLVIDAS 1 a edição ISBN 978-85-917238-0-5 João Pessoa Edição do Autor 2014 Prefácio Este texto foi elaborado para a disciplina Introdução
LENIMAR NUNES DE ANDRADE INTRODUÇÃO À ÁLGEBRA: QUESTÕES COMENTADAS E RESOLVIDAS 1 a edição ISBN 978-85-917238-0-5 João Pessoa Edição do Autor 2014 Prefácio Este texto foi elaborado para a disciplina Introdução
MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIAS
 MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIS Como vimos no módulo 1, para que nós possamos extrair dos dados estatísticos de que dispomos a correta análise e interpretação, o primeiro passo deverá ser a correta
MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIS Como vimos no módulo 1, para que nós possamos extrair dos dados estatísticos de que dispomos a correta análise e interpretação, o primeiro passo deverá ser a correta
