FATEC Faculdade de Tecnologia de São Paulo Movimento de Terra e Pavimentação ETE II Estudo de traçado de Estradas - II
|
|
|
- Roberto Macedo Frade
- 8 Há anos
- Visualizações:
Transcrição
1 1 COORDEADAS, AZIMUTES E ÂGULOS DE DEFLEXÃO estas notas de aula pretende-se apresentar as formas de cálculos de obtenção dos valores de azimutes de trechos de tangentes de rodovias e também os cálculos necessários para a obtenção dos valores das coordenadas das estacas de trechos em tangente e estacas de trechos em curva. 1- Locação do Projeto em Planta Como o traçado das estradas é uma poligonal aberta os projetos, (os desenhos) apresenta o desenvolvimento de seus traçados da esquerda para a direita. Assim faz-se necessário a adequação do da locação do projeto na folha. Por exemplo, um projeto de uma rodovia de Santos-SP a Bauru-SP, o trecho compreendido entre os pontos A e B, quando representados em planta, o ponto A estaria a esquerda e o ponto B à direita. Observe-se que a rosa dos ventos quando no mapa apresentava o norte sempre para cima (norma) e quando da representação do trecho em questão sofreu um giro de maneira a permitir a locação do trecho da esquerda para a direita. Planta Bauru B E A B A E Santos 2- Cálculo de Azimutes e Comprimentos de Alinhamento Pode-se calcular o azimute e o comprimento de um alinhamento a partir de suas coordenadas (, E), utilizando as equações 1, 2, 3, 4 e 5 abaixo.
2 2 i+1 Az i L P i+1 i P i E i+1 (Fig.1) E i E E Baseado na figura 01 pode-se definir as seguintes relações (0 o <Az i <90 o ) Az i = arctg ((E i+1 )-E i )/(( i+1 )- i ) (eq-1) 1Q. (90 o <Az i <180 o ) Az i = 180 o - arctg ((E i+1 )-E i )/(( i+1 )- i ) (eq-2) 2Q. (180 o <Az i <270 o ) Az i = 180 o + arctg ((E i+1 )-E i )/(( i+1 )- i ) (eq-3) 3Q. (270 o <Az i <360 o ) Az i = 360 o - arctg ((E i+1 )-E i )/(( i+1 )- i ) (eq-4) 4Q. L = ((E i+1 )-E i ) 2 + ( i+1 )- i ) 2 ) 1/2 = (( E) 2 + ( ) 2 ) 1/2 (eq-5) 3- Cálculo das Coordenadas Retangulares de uma Poligonal. Pode-se determinar os valores das coordenadas das estacas, tanto de trechos em tangentes como também de curvas. Conhecendo-se as coordenadas de um dado ponto o azimute e a distância à um segundo ponto, pode-se determinar as coordenadas ( ; E) desse segundo ponto através das equações 6 e 7. E B α 1 i+1 α o L o (Fig.2) Ai A L 1 C 0 E o E
3 3 Para a determinação das coordenadas ( e E) do ponto B da figura 02, tem-se: B = Ai + = L o cos α o B = Ai + L o cos α o (eq-6) E B = E Ai + E E = L o sen α o E B = E Ai + L o sen α o (eq-7) Observe-se que para a obtenção do incremento (azimute) na equação 6, utilizamos a função co-seno que corresponde ao eixo das coordenadas E e o incremento E (azimute) na equação utilizamos a função seno que corresponde ao eixo trigonométrico. Isso se deve ao fato de no círculo trigonométrico o sentido de utilização é anti-horário e no círculo de azimute o sentido é horário e eles estão defasados de 90º. 4- Localização do Quadrante em Função das Coordenadas, E Procedimento para a determinação do azimute α o da primeira tangente da Figura 2, partindo dos valores das coordenadas dos pontos A e B. E (-) E (+) W (+) (+) E (Fig. 3) E (-) (-) E (+) (-) S Para a determinação do rumo utiliza-se a equação 8 abaixo. O rumo que indica a direção do ponto A para o ponto B, é o arctg da diferença de coordenada E B E A dividido pela diferença da coordenada B A. Observe-se que, para a obtenção do rumo de A para B é a coordenada do ponto B menos a coordenada do ponto A.
4 O ângulo obtido é o rumo de A para B. 4 Rumo (E B E A ) = arctg (E+ ou E-) (eq-8) ( B A ) (+ ou -) Uma vez obtida a diferença de coordenadas E e deve-se observar o sinal e compara-lo com a fig 3 acima, donde se deduz o quadrante em que o rumo se encontra, em seguida transforma-se o rumo em azimute com auxílio da tabela 01, abaixo. TABELA 01 Valores de Azimute em Função do Rumo QUADRATE AZIMUTE E Az = Rumo SE Az = 180 o Rumo SW Az = 180 o + Rumo W Az = 360 o - Rumo 5 - Exemplo I Sabendo-se as coordenadas de três pontos Pi, A e B de maneira que os pontos A e B estão localizados sobre as tangentes 1 e 2 respectivamente, deseja-se locar uma curva com espirais de transição intercalada com uma secção de trecho circular, sabe-se que o projeto se desenvolverá no sentido de A para B, pede-se Os azimutes das duas tangentes; As coordenadas dos pontos notáveis Coordenadas de uma estaca locada dentro da primeira espiral ( ) Coordenada de uma estaca locada dentro do trecho circular ( ) Tabela de locação das estacas por deflexões (iº) Dados: -Estaca do Pi = ,51m -Superelevação máxima 9% (adotar valores inferiores - Método AASHTO) -Velocidade diretriz = 80km/h 6.1- Cálculo dos Azimutes Pontos Coordenadas (m) E Pi A B
5 Azimute da tangente 1 - (de A para Pi) 5 (+) Rumo (tangente 1) = arctg ((EPi EA)/(Pi A)) sinal (+) portanto quadrante (E) 1 o quadrante Azimute = Rumo Rumo= arctg (( )/( )) = 323 Rumo=arctg = arctg 0,8075 = 38,9208 o 400 portanto Az A PI (tangente1) = 38,9208 o Importante: o número de casas após a vírgula, principalmente em se tratando de ângulos, deve ser considerados várias casas (mínimo 4), quando se envolve esses valores em contas, para a obtenção de valores mais representativos. Entretanto, a representação, ou seja, a transcrição do valor, pode ser feita com 2, 3 ou mesmo 4 casas. Azimute da tangente 2 - (de Pi para B) (+) Rumo (tangente 2) = arctg ((EB EPi)/(B Pi)) sinal (-) portanto quadrante (SE) 2 o quadrante Azimute = 180 O - Rumo Rumo= arctg (( )/( )) = 575 Rumo=arctg = 415 arctg = 54,1805 o portanto Az (tangente2) = 180 O 54,1805 o = 125,8194 o 6.2- Cálculo do ângulo central ÂC = Az (tangente 2) Az (tangente 1) ÂC = 125,8194 o - 38,9208 o = 86,8985 o ÂC = 86,8985 o (ângulo plano decimal) ou 1,51667º (rd) Para transformação de ângulo plano em ângulo radiano, algumas calculadoras o fazem diretamente, entretanto, outras não, assim, deve-se multiplicar o ângulo plano por π e dividir por 180º. O inverso, transformar ângulo radiano em ângulo plano, multiplica-se o ângulo radiano por 180º e divide-se pó π.
6 Determinação dos pontos notáveis da curva de transição (TS, SC, CS e ST) Adotando-se uma superelevação de 7,4% para uma velocidade diretriz de 80 km/h com o método da AASHTO tem-se um Rc de 382m Dados Curva circular de Rc = 382m ÂC = 86,8985 o Posição do PI = ,51m Velocidade Diretriz = 80 km/h Resolução: Vd Ie min = 0,035 x Rc = 0,035 x = 46,91m Adotaremos Ie = 90m (Ie = 2 * Ie min. ) Elementos principais da curva I 2 90 θs = = = 0,11780 rd = o 2 Rc Ie 2 x 382 θs 2 0, Xs = Ie x ( ) = 90 x ( ) = 89,88m θs 0,11780 Ys = Ie x ( ) = 90 x ( ) = 3.53m 3 3 Elementos de posição de transição K = Xs - Rc senθs = 89, sen o = 45,02m Afastamento da curva p = Ys Rc x(1 - cosθs) = 3, x (1 - cos o ) = 0.88m Tangente total - TT TT = k + (Rc + p) x tg(âc/2) = TT = 45,02 + ( ,88) x tg(86,8985 o /2) =407,71m Desenvolvimento do trecho circular
7 7 D = Rc x (ÂC 2 x θs) = D = 382 x (1,51667rd 2 x 0,11780rd) = 489,37m Corda (c) c 2 = Xs 2 + Ys 2 = c = (89, ,53 2 ) 1/2 = 89,94m Deflexão is is = arctg Ys/Xs = artg(3,53 / 99,88) = 2,2491º Estacas dos pontos principais Estaca TS = estaca Pi TT = ( ,51m) 407,71= ,22 m Estaca SC = estaca TS + Ie = ( ,22m) + 90m = ,22 m Estaca CS = estaca.sc + D = ( ,22m)+489,37m = ,59 m Estaca SC = estaca CS + Ie = ( ,59m)+90m = ,59 m Calculo Das Coordenadas Dos Pontos otáveis Coordenada da estaca TS Figura 04 Azimute de PI para TS Observe o Azimute é de Pi para TS = Az TS PI = (38,9208 o o ) = 218,9208 o TS = Pi +TT cos Az PI TS = TS = ,71 cos 218,9208 o = ,80m E TS = E PI + TT sem Az PI TS = E TS = ,71 sem 218,9208 o = ,85m
8 8 Coordenada da estaca SC Figura 05 Azimute de TS para SC Observe o Azimute é de TS para SC = Az TS PI + isº = (38,9208 o + 2,2491 o ) = 41,1699 o SC = TS + c x cos (Az TS PI + is) = SC = ,80+ 89,84 x cos (41,1699 o ) = SC = ,50m E SC = E TS + c x sen (Az TS PI + is) = E SC = , ,94 x sen (41,1699 o ) = E SC = ,06m Cálculo da Coordenada CC
9 Figura 06 Azimute de SC para CC 9 Observe o Azimute é de SC para CC = Az TS PI + 90º + θs = (38,9208 o + 90 o o ) = 135,41468 o CC = SC + Rc x cos (Az TS PI + 90 o + θs) = CC = , x cos (135,41468 o ) = CC = ,25m E CC = E SC + Rc x sen (Az TS PI + 90 o + θs) = E CC = , x sen (135,41468 o ) = E CC = ,99m Cálculo da Coordenada ST Figura 07 Azimute de PI para ST Observe o Azimute que dá a direção de PI para ST já foi calculado anteriormente Az PI ST = 125,8194 o ST = Pi + TT cos Az PI ST = ST = ,71 cos 125,8194 o E ST = E Pi + TT sen Az PI ST = E ST = ,71 sen 125,8194 o = ,34 m = ,60m Cálculo da Coordenada CS
10 10 Figura 08 Azimute de ST para CS Observe o Azimute é de ST para CS = Az ST CS = Az PI ST + 180º isº = (125,8194 o o 2,2491º) = 303,5703 o CS = ST + c * cos (Az ST CS ) = CS = , ,94 * cos (303,5703º) = CS = ,08m E CS = E G + c * sen (Az ST CS ) = E CS = , ,94 * sen (303,5703º) = E CS = ,65m Tabela de coordenadas dos pontos notáveis Pontos Coordenadas (m) E TS , ,85 SC , ,06 CC , ,99 CS , ,65 ST , ,60 PI , ,00
11 LOCAÇÃO DE CURVA COM ESPIRAIS DE TRASIÇÃO COM COORDEADAS PI TS SC CS ST CC E
Aula 8 : Desenho Topográfico
 Aula 8 : Desenho Topográfico Topografia, do grego topos (lugar) e graphein (descrever), é a ciência aplicada que representa, no papel, a configuração (contorno,dimensão e posição relativa) de um porção
Aula 8 : Desenho Topográfico Topografia, do grego topos (lugar) e graphein (descrever), é a ciência aplicada que representa, no papel, a configuração (contorno,dimensão e posição relativa) de um porção
Coordenadas Polares. Prof. Márcio Nascimento. marcio@matematicauva.org
 Coordenadas Polares Prof. Márcio Nascimento marcio@matematicauva.org Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática
Coordenadas Polares Prof. Márcio Nascimento marcio@matematicauva.org Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática
UNICAP Universidade Católica de Pernambuco Prof. Glauber Carvalho Costa Estradas 1
 1 a QUESTÃO Supondo que você é o engenheiro responsável pela elaboração do projeto geométrico do Arco Metropolitano do Recife, projeto que irá conectar o pólo de desenvolvimento industrial do litoral norte
1 a QUESTÃO Supondo que você é o engenheiro responsável pela elaboração do projeto geométrico do Arco Metropolitano do Recife, projeto que irá conectar o pólo de desenvolvimento industrial do litoral norte
-ESTRUTURA VIÁRIA TT048 CURVAS VERTICAIS
 INFRAINFRA -ESTRUTURA VIÁRIA TT048 CURVAS VERTICAIS Prof. Djalma Pereira Prof. Eduardo Ratton Profa. Gilza Fernandes Blasi Profa. Márcia de Andrade Pereira Um fator importante para a segurança e eficiência
INFRAINFRA -ESTRUTURA VIÁRIA TT048 CURVAS VERTICAIS Prof. Djalma Pereira Prof. Eduardo Ratton Profa. Gilza Fernandes Blasi Profa. Márcia de Andrade Pereira Um fator importante para a segurança e eficiência
Início E. 2345+13,98. UNICAP Universidade Católica de Pernambuco Prof. Glauber Carvalho Costa Estradas 1. 1 a QUESTÃO
 1 a QUESTÃO Supondo que você foi designado para desenvolver o projeto geométrico do Arco Metropolitano do Recife, que corresponderá a uma o obra rodoviária ligando a região norte do estado, próximo ao
1 a QUESTÃO Supondo que você foi designado para desenvolver o projeto geométrico do Arco Metropolitano do Recife, que corresponderá a uma o obra rodoviária ligando a região norte do estado, próximo ao
7 AULA. Curvas Polares LIVRO. META Estudar as curvas planas em coordenadas polares (Curvas Polares).
 1 LIVRO Curvas Polares 7 AULA META Estudar as curvas planas em coordenadas polares (Curvas Polares). OBJETIVOS Estudar movimentos de partículas no plano. Cálculos com curvas planas em coordenadas polares.
1 LIVRO Curvas Polares 7 AULA META Estudar as curvas planas em coordenadas polares (Curvas Polares). OBJETIVOS Estudar movimentos de partículas no plano. Cálculos com curvas planas em coordenadas polares.
Prof. Rossini Bezerra Faculdade Boa Viagem
 Sistemas de Coordenadas Polares Prof. Rossini Bezerra Faculdade Boa Viagem Coordenadas Polares Dado um ponto P do plano, utilizando coordenadas cartesianas (retangulares), descrevemos sua localização no
Sistemas de Coordenadas Polares Prof. Rossini Bezerra Faculdade Boa Viagem Coordenadas Polares Dado um ponto P do plano, utilizando coordenadas cartesianas (retangulares), descrevemos sua localização no
CURVAS HORIZONTAIS COM TRANSIÇÃO
 CURVAS HORIZONTAIS COM TRANSIÇÃO Introdução Trecho reto para uma curva circular: Variação instantânea do raio infinito para o raio finito da curva circular Surgimento brusco de uma força centrífuga Desconforto
CURVAS HORIZONTAIS COM TRANSIÇÃO Introdução Trecho reto para uma curva circular: Variação instantânea do raio infinito para o raio finito da curva circular Surgimento brusco de uma força centrífuga Desconforto
FATEC Faculdade de Tecnologia de Pavimentação Departamento de Transportes e Obras de Terra - Prof. Edson 4- CURVAS HORIZONTAIS DE TRANSIÇÃO
 4- CURVAS HORIZONTAIS DE TRANSIÇÃO 4.1 INTRODUÇÃO Quando um veículo passa pelo ponto PC ponto de começo da curva circular horizontal ou PT ponto de término da curva circular horizontal, dependendo do comprimento
4- CURVAS HORIZONTAIS DE TRANSIÇÃO 4.1 INTRODUÇÃO Quando um veículo passa pelo ponto PC ponto de começo da curva circular horizontal ou PT ponto de término da curva circular horizontal, dependendo do comprimento
Comprimentos de Curvas e Coordenadas Polares Aula 38
 Comprimentos de Curvas e Coordenadas Polares Aula 38 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 12 de Junho de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia
Comprimentos de Curvas e Coordenadas Polares Aula 38 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 12 de Junho de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia
08-LEVANTAMENTO TOPOGRÁFICO PLANIMETRIA pg 98
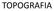 TOPOGRAFIA 08-LEVANTAMENTO TOPOGRÁFICO PLANIMETRIA pg 98 levantamento pontos planimétricos, altimétricos ou planialtimétricos pontos de apoio (partir destes ) Projeção ΔX = D. sen Az ΔY = D. cos Az TÉCNICAS
TOPOGRAFIA 08-LEVANTAMENTO TOPOGRÁFICO PLANIMETRIA pg 98 levantamento pontos planimétricos, altimétricos ou planialtimétricos pontos de apoio (partir destes ) Projeção ΔX = D. sen Az ΔY = D. cos Az TÉCNICAS
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
CURVAS HORIZONTAIS COM TRANSIÇÃO
 CURVAS HORIZONTAIS COM TRANSIÇÃO INTRODUÇÃO A definição do traçado de uma estrada por meio de linhas retas concordando diretamente com curvas circulares cria problemas nos pontos de concordância. A descontinuidade
CURVAS HORIZONTAIS COM TRANSIÇÃO INTRODUÇÃO A definição do traçado de uma estrada por meio de linhas retas concordando diretamente com curvas circulares cria problemas nos pontos de concordância. A descontinuidade
UNIVERSIDADE FEDERAL DO PARÁ CENTRO DE GEOCIÊNCIAS DEPARTAMENTO DE GEOLOGIA DISCIPLINA: GEOLOGIA ESTRUTURAL GEOLOGIA ESTRUTURAL - PRÁTICA
 1 UNIVERSIDADE FEDERAL DO PARÁ CENTRO DE GEOCIÊNCIAS DEPARTAMENTO DE GEOLOGIA DISCIPLINA: GEOLOGIA ESTRUTURAL Cap. 01 - Mapas e Seções Geológicas GEOLOGIA ESTRUTURAL - PRÁTICA Antes que se comece a estudar
1 UNIVERSIDADE FEDERAL DO PARÁ CENTRO DE GEOCIÊNCIAS DEPARTAMENTO DE GEOLOGIA DISCIPLINA: GEOLOGIA ESTRUTURAL Cap. 01 - Mapas e Seções Geológicas GEOLOGIA ESTRUTURAL - PRÁTICA Antes que se comece a estudar
A definição do traçado de uma estrada por meio de linhas retas concordando diretamente com curvas circulares cria problema nos pontos de concordância.
 4.1.2 Curvas Horizontais com Transição A definição do traçado de uma estrada por meio de linhas retas concordando diretamente com curvas circulares cria problema nos pontos de concordância. Assim, é necessário
4.1.2 Curvas Horizontais com Transição A definição do traçado de uma estrada por meio de linhas retas concordando diretamente com curvas circulares cria problema nos pontos de concordância. Assim, é necessário
Noções de Topografia Para Projetos Rodoviarios
 Página 1 de 8 Noções de Topografia Para Projetos Rodoviarios Capitulos 01 - Requisitos 02 - Etaqpas 03 - Traçado 04 - Trafego e Clssificação 05 - Geometria 06 - Caracteristicas Técnicas 07 - Distancia
Página 1 de 8 Noções de Topografia Para Projetos Rodoviarios Capitulos 01 - Requisitos 02 - Etaqpas 03 - Traçado 04 - Trafego e Clssificação 05 - Geometria 06 - Caracteristicas Técnicas 07 - Distancia
Lista de Exercícios de Topografia Planimetria
 Lista de Exercícios de Topografia Planimetria 1. Cite 3 métodos de levantamento topográfico e uma situação prática onde cada um poderia ser empregado. 2. Verifique se existe erro de fechamento angular
Lista de Exercícios de Topografia Planimetria 1. Cite 3 métodos de levantamento topográfico e uma situação prática onde cada um poderia ser empregado. 2. Verifique se existe erro de fechamento angular
Projeto Geométrico Horizontal
 UNICAP Universidade Católica de Pernambuco Prof. Glauber Carvalho Costa Estrada 1 Projeto Geométrico Horizontal Aula 4 Recife, 2016 Elementos Planimétricos de uma Estrada Curvas de Concordância Horizontal
UNICAP Universidade Católica de Pernambuco Prof. Glauber Carvalho Costa Estrada 1 Projeto Geométrico Horizontal Aula 4 Recife, 2016 Elementos Planimétricos de uma Estrada Curvas de Concordância Horizontal
Coordenadas Polares Mauri C. Nascimento Dep. De Matemática FC Unesp/Bauru
 Coordenadas Polares Mauri C. Nascimento Dep. De Matemática FC Unesp/Bauru Dado um ponto P do plano, utilizando coordenadas cartesianas (retangulares), descrevemos sua localização no plano escrevendo P
Coordenadas Polares Mauri C. Nascimento Dep. De Matemática FC Unesp/Bauru Dado um ponto P do plano, utilizando coordenadas cartesianas (retangulares), descrevemos sua localização no plano escrevendo P
DEPARTAMENTO DE ENGENHARIA DE BIOSSISTEMAS - ESALQ / USP LEB 340 - Topografia e Geoprocessamento I Prof. Rubens Angulo Filho 1º Semestre de 2015
 Trabalho prático nº 01: Levantamento à Trena 1) Material: a) trena de 20,0m; b) 3 balizas; c) 4 fichas; d) GPS de navegação 2) Método: A medição dos alinhamentos, no campo, será executada por 3 balizeiros
Trabalho prático nº 01: Levantamento à Trena 1) Material: a) trena de 20,0m; b) 3 balizas; c) 4 fichas; d) GPS de navegação 2) Método: A medição dos alinhamentos, no campo, será executada por 3 balizeiros
Campos Vetoriais e Integrais de Linha
 Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Cálculo em Computadores - 2007 - trajectórias 1. Trajectórias Planas. 1 Trajectórias. 4.3 exercícios... 6. 4 Coordenadas polares 5
 Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
EXERCÍCIOS DE TOPOGRAFIA
 UNIVERSIDADE DE SÃO PAULO Escola Superior de Agricultura "Luiz de Queiroz" DEPARTAMENTO DE ENGENHARIA RURAL Área de Topografia e Geoprocessamento 1 EXERCÍCIOS DE TOPOGRAFIA Professores: Rubens Angulo Filho
UNIVERSIDADE DE SÃO PAULO Escola Superior de Agricultura "Luiz de Queiroz" DEPARTAMENTO DE ENGENHARIA RURAL Área de Topografia e Geoprocessamento 1 EXERCÍCIOS DE TOPOGRAFIA Professores: Rubens Angulo Filho
Introdução à Topografia
 Topografia Introdução à Topografia Etimologicamente a palavra TOPOS, em grego, significa lugar e GRAPHEN descrição, assim, de uma forma bastante simples, Topografia significa descrição do lugar. O termo
Topografia Introdução à Topografia Etimologicamente a palavra TOPOS, em grego, significa lugar e GRAPHEN descrição, assim, de uma forma bastante simples, Topografia significa descrição do lugar. O termo
= 30maneiras para sentar-se. Como são 20 filas, o número total de maneiras distintas que atende ao enunciado será:
 TEÁTIC 1ª QUESTÃO Um avião possui 10 poltronas de passageiros distribuídas em 0 filas. Cada fila tem poltronas do lado esquerdo (denotadas por, B, C) e do lado direito (denotadas por D, E, F), separadas
TEÁTIC 1ª QUESTÃO Um avião possui 10 poltronas de passageiros distribuídas em 0 filas. Cada fila tem poltronas do lado esquerdo (denotadas por, B, C) e do lado direito (denotadas por D, E, F), separadas
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
AMARELA EFOMM-2008 AMARELA
 PROVA DE MATEMÁTICA EFOMM-008 1ª Questão: A figura acima representa uma caixa de presente de papelão que mede 16 por 30 centímetros. Ao cortarmos fora os quadrados do mesmo tamanho dos quatro cantos e
PROVA DE MATEMÁTICA EFOMM-008 1ª Questão: A figura acima representa uma caixa de presente de papelão que mede 16 por 30 centímetros. Ao cortarmos fora os quadrados do mesmo tamanho dos quatro cantos e
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Levantamento. Levantamento altimétrico:
 Levantamento planimétrico trico: projeção plana que não traz informações acerca do relevo do terreno levantado; somente acerca de informações relativas à medições feitas na horizontal. Levantamento altimétrico:
Levantamento planimétrico trico: projeção plana que não traz informações acerca do relevo do terreno levantado; somente acerca de informações relativas à medições feitas na horizontal. Levantamento altimétrico:
Refração da Luz Prismas
 Refração da Luz Prismas 1. (Fuvest 014) Um prisma triangular desvia um feixe de luz verde de um ângulo θ A, em relação à direção de incidência, como ilustra a figura A, abaixo. Se uma placa plana, do mesmo
Refração da Luz Prismas 1. (Fuvest 014) Um prisma triangular desvia um feixe de luz verde de um ângulo θ A, em relação à direção de incidência, como ilustra a figura A, abaixo. Se uma placa plana, do mesmo
CAP. 3 - EXTENSÔMETROS - "STRAIN GAGES" Exemplo: extensômetro Huggenberger
 CAP. 3 - EXTENSÔMETOS - "STAIN GAGES" 3. - Extensômetros Mecânicos Exemplo: extensômetro Huggenberger Baseia-se na multiplicação do deslocamento através de mecanismos de alavancas. Da figura: l' = (w /
CAP. 3 - EXTENSÔMETOS - "STAIN GAGES" 3. - Extensômetros Mecânicos Exemplo: extensômetro Huggenberger Baseia-se na multiplicação do deslocamento através de mecanismos de alavancas. Da figura: l' = (w /
Manual de Laboratório Física Experimental I- Hatsumi Mukai e Paulo R.G. Fernandes
 Pêndulo Simples 6.1 Introdução: Capítulo 6 Um pêndulo simples se define como uma massa m suspensa por um fio inextensível, de comprimento com massa desprezível em relação ao valor de m. Se a massa se desloca
Pêndulo Simples 6.1 Introdução: Capítulo 6 Um pêndulo simples se define como uma massa m suspensa por um fio inextensível, de comprimento com massa desprezível em relação ao valor de m. Se a massa se desloca
Engenharia Civil. Alexandre Souza Eng. Agrimensor MSc. alexandre0363@gmail.com
 Engenharia Civil Alexandre Souza Eng. Agrimensor MSc. alexandre0363@gmail.com Levantamento topográfico -Planimetria Em um levantamento topográfico, normalmente são determinados pontos de apoio ao levantamento
Engenharia Civil Alexandre Souza Eng. Agrimensor MSc. alexandre0363@gmail.com Levantamento topográfico -Planimetria Em um levantamento topográfico, normalmente são determinados pontos de apoio ao levantamento
LISTA 10 INDUÇÃO ELETROMAGNÉTICA
 1. (Ufmg 95) Esta figura mostra uma espira retangular, de lados a = 0,20 m e b = 0,50 m, sendo empurrada, com velocidade constante v = 0,50 m/s, para uma região onde existe um campo magnético uniforme
1. (Ufmg 95) Esta figura mostra uma espira retangular, de lados a = 0,20 m e b = 0,50 m, sendo empurrada, com velocidade constante v = 0,50 m/s, para uma região onde existe um campo magnético uniforme
Curvas em coordenadas polares
 1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
TEORIA UNIDIMENSIONAL DAS
 Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade alansulato@ufpr.br INTRODUÇÃO: O conhecimento das velocidades do fluxo de
Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade alansulato@ufpr.br INTRODUÇÃO: O conhecimento das velocidades do fluxo de
24/Abril/2013 Aula 19. Equação de Schrödinger. Aplicações: 1º partícula numa caixa de potencial. 22/Abr/2013 Aula 18
 /Abr/013 Aula 18 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda e níveis
/Abr/013 Aula 18 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda e níveis
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Mestrado Integrado em Engenharia Aeroespacial Aerodinâmica I. Fluido Perfeito
 Mestrado Integrado em Engenharia Aeroespacial Aerodinâmica I Fluido Perfeito 1. Considere o escoamento bidimensional, irrotacional e incompressível definido pelo potencial φ = a) Mostre que φ satisfaz
Mestrado Integrado em Engenharia Aeroespacial Aerodinâmica I Fluido Perfeito 1. Considere o escoamento bidimensional, irrotacional e incompressível definido pelo potencial φ = a) Mostre que φ satisfaz
CAPÍTULO VI TRANSPORTE DE COORDENADAS RETANGULARES POLIGONAIS FECHADAS
 CAPÍTULO VI TRANSPORTE DE COORDENADAS RETANGULARES POLIGONAIS FECHADAS 1 o ) Durante o levantamento topográfico planimétrico foram medidos os seguintes valores angulares relativos a uma poligonal fechada:
CAPÍTULO VI TRANSPORTE DE COORDENADAS RETANGULARES POLIGONAIS FECHADAS 1 o ) Durante o levantamento topográfico planimétrico foram medidos os seguintes valores angulares relativos a uma poligonal fechada:
Conceitos Básicos de Desenho Técnico
 Conceitos Básicos de Desenho Técnico 1. Escalas Gráficas e Numéricas 1.1. Definição No desenho arquitetônico, a necessidade de representar espacialmente objetos e seus detalhes através de desenhos, fez
Conceitos Básicos de Desenho Técnico 1. Escalas Gráficas e Numéricas 1.1. Definição No desenho arquitetônico, a necessidade de representar espacialmente objetos e seus detalhes através de desenhos, fez
Faculdades Anhanguera
 2º Aula de Física 2.1 Posição A posição de uma partícula sobre um eixo x localiza a partícula em relação á origem, ou ponto zero do eixo. A posição é positiva ou negativa, dependendo do lado da origem
2º Aula de Física 2.1 Posição A posição de uma partícula sobre um eixo x localiza a partícula em relação á origem, ou ponto zero do eixo. A posição é positiva ou negativa, dependendo do lado da origem
EXEMPLO NUMÉRICO DE LEVANTAMENTO PLANIMÉTRICO PELO MÉTODO DE CAMINHAMENTO (POLIGONAÇÃO)
 EXEMPLO NUMÉRICO DE LEVANTAMENTO PLANIMÉTRICO PELO MÉTODO DE CAMINHAMENTO (POLIGONAÇÃO) Distâncias 1º etapa: leitura dos fios estadimétricos (fio superior - FS, fio médio - FM, fio inferior - FI) FIOS
EXEMPLO NUMÉRICO DE LEVANTAMENTO PLANIMÉTRICO PELO MÉTODO DE CAMINHAMENTO (POLIGONAÇÃO) Distâncias 1º etapa: leitura dos fios estadimétricos (fio superior - FS, fio médio - FM, fio inferior - FI) FIOS
VESTIBULAR 2004 - MATEMÁTICA
 01. Dividir um número real não-nulo por 0,065 é equivalente a multiplicá-lo por: VESTIBULAR 004 - MATEMÁTICA a) 4 c) 16 e) 1 b) 8 d) 0. Se k é um número inteiro positivo, então o conjunto A formado pelos
01. Dividir um número real não-nulo por 0,065 é equivalente a multiplicá-lo por: VESTIBULAR 004 - MATEMÁTICA a) 4 c) 16 e) 1 b) 8 d) 0. Se k é um número inteiro positivo, então o conjunto A formado pelos
DIRETRIZES PARA DESENVOLVIMENTO DE UM SISTEMA AVANÇADO PARA ESTUDOS E PROJETOS VIÁRIOS: DEFINIÇÃO, REPRESENTAÇÃO E ANÁLISE DO EIXO PLANIMÉTRICO
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA CIVIL Fernando Fraga de Freitas dos Santos DIRETRIZES PARA DESENVOLVIMENTO DE UM SISTEMA AVANÇADO PARA ESTUDOS
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA CIVIL Fernando Fraga de Freitas dos Santos DIRETRIZES PARA DESENVOLVIMENTO DE UM SISTEMA AVANÇADO PARA ESTUDOS
EXAME NACIONAL DO ENSINO SECUNDÁRIO VERSÃO 1
 EXAME NACIONAL DO ENSINO SECUNDÁRIO 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) Cursos Gerais e Cursos Tecnológicos PROVA 435/9 Págs. Duração da prova: 120 minutos 2005 1.ª FASE
EXAME NACIONAL DO ENSINO SECUNDÁRIO 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) Cursos Gerais e Cursos Tecnológicos PROVA 435/9 Págs. Duração da prova: 120 minutos 2005 1.ª FASE
3.4 Movimento ao longo de uma curva no espaço (terça parte)
 3.4-41 3.4 Movimento ao longo de uma curva no espaço (terça parte) Antes de começar com a nova matéria, vamos considerar um problema sobre o material recentemente visto. Problema: (Projeção de uma trajetória
3.4-41 3.4 Movimento ao longo de uma curva no espaço (terça parte) Antes de começar com a nova matéria, vamos considerar um problema sobre o material recentemente visto. Problema: (Projeção de uma trajetória
Exercícios do item 1.6: 1) Calcule as reações nos apoios da viga abaixo.
 Exercícios do item 1.5: 1) Calcule a força de tração nas duas barras da estrutura abaixo. tan θ 0 1 θ1 arc tan (0,75) θ1, 87 tan θ 0 θ arc tan (1,) θ 5, 1 o x 0 : 1 cos (,87 ) cos(5,1 ) 0 0, 0,8 1 0,8
Exercícios do item 1.5: 1) Calcule a força de tração nas duas barras da estrutura abaixo. tan θ 0 1 θ1 arc tan (0,75) θ1, 87 tan θ 0 θ arc tan (1,) θ 5, 1 o x 0 : 1 cos (,87 ) cos(5,1 ) 0 0, 0,8 1 0,8
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Civil. Mecânica Vetorial ENG01035
 Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Civil EXERCÍCIOS D 2 a. ÁRE Mecânica Vetorial ENG035 LIST DE PROLEMS DE PROV CENTRO DE GRVIDDE 1) peça representada
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Civil EXERCÍCIOS D 2 a. ÁRE Mecânica Vetorial ENG035 LIST DE PROLEMS DE PROV CENTRO DE GRVIDDE 1) peça representada
CAMPOS MAGNÉTICOS PRODUZIDOS POR CORRENTES
 Física (Eletromagnetismo) 1. Lei de iot-savart CAMPOS MAGNÉTICOS PRODUZIDOS POR CORRENTES A lei de iot-savart é uma lei no eletromagnetismo que descreve o vetor indução magnética em termos de magnitude
Física (Eletromagnetismo) 1. Lei de iot-savart CAMPOS MAGNÉTICOS PRODUZIDOS POR CORRENTES A lei de iot-savart é uma lei no eletromagnetismo que descreve o vetor indução magnética em termos de magnitude
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Professor: Renato Medeiros EXERCÍCIOS NOTA DE AULA IV Goiânia - 2014 EXERCÍCIOS 1. Uma partícula eletrizada positivamente é
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Professor: Renato Medeiros EXERCÍCIOS NOTA DE AULA IV Goiânia - 2014 EXERCÍCIOS 1. Uma partícula eletrizada positivamente é
Escola Básica e Secundária de Velas
 Escola Básica e Secundária de Velas Planificação Anual do 12º Ano Matemática A Ano letivo 2015 /2016 1º Período 2º Período 3º Período Nº DE BLOCOS PREVISTOS 39 32 24 Apresentação 0,5 1º Período 2º Período
Escola Básica e Secundária de Velas Planificação Anual do 12º Ano Matemática A Ano letivo 2015 /2016 1º Período 2º Período 3º Período Nº DE BLOCOS PREVISTOS 39 32 24 Apresentação 0,5 1º Período 2º Período
FÍSICA - 3 o ANO MÓDULO 13 CINEMÁTICA VETORIAL E COMPOSIÇÃO DE MOVIMENTOS
 FÍSICA - 3 o ANO MÓDULO 13 CINEMÁTICA VETORIAL E COMPOSIÇÃO DE MOVIMENTOS Como pode cair no enem (UERJ) Pardal é a denominação popular do dispositivo óptico-eletrônico utilizado para fotografar veículos
FÍSICA - 3 o ANO MÓDULO 13 CINEMÁTICA VETORIAL E COMPOSIÇÃO DE MOVIMENTOS Como pode cair no enem (UERJ) Pardal é a denominação popular do dispositivo óptico-eletrônico utilizado para fotografar veículos
CORTESIA Prof. Renato Brito www.vestseller.com.br Espaço
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA ESTIBULAR 983/984 PROA DE FÍSICA 0. (ITA-84) Colocou-se uma certa quantidade de bolinhas de chumbo numa seringa plástica e o volume lido na própria escala da seringa
INSTITUTO TECNOLÓGICO DE AERONÁUTICA ESTIBULAR 983/984 PROA DE FÍSICA 0. (ITA-84) Colocou-se uma certa quantidade de bolinhas de chumbo numa seringa plástica e o volume lido na própria escala da seringa
PROJETO GEOMÉTRICO DE RODOVIAS
 PROJETO GEOMÉTRICO DE RODOVIAS Curso: 7º Período - Engenharia de Agrimensura e Cartográfica Prof. Paulo Augusto F. Borges CURVAS HORIZONTAIS CIRCULARES 1. Introdução O traçado de uma rodovia é constituído
PROJETO GEOMÉTRICO DE RODOVIAS Curso: 7º Período - Engenharia de Agrimensura e Cartográfica Prof. Paulo Augusto F. Borges CURVAS HORIZONTAIS CIRCULARES 1. Introdução O traçado de uma rodovia é constituído
Nestas condições, determine a) as coordenadas dos vértices B, C, D, E e F e a área do hexágono ABCDEF. b) o valor do cosseno do ângulo AÔB.
 MATEMÁTICA 0 A figura representa, em um sistema ortogonal de coordenadas, duas retas, r e s, simétricas em relação ao eixo Oy, uma circunferência com centro na origem do sistema, e os pontos A = (1, ),
MATEMÁTICA 0 A figura representa, em um sistema ortogonal de coordenadas, duas retas, r e s, simétricas em relação ao eixo Oy, uma circunferência com centro na origem do sistema, e os pontos A = (1, ),
Topografia Aplicada à Engenharia Civil AULA 07
 Topografia Geomática Aplicada à Engenharia Civil AULA 07 Poligonação Parte 1 Laboratório de Cartografia Digital - CTUFES Poligonação ou Caminhamento 2 A6 3 A6 Poligonação ou Caminhamento Este processo
Topografia Geomática Aplicada à Engenharia Civil AULA 07 Poligonação Parte 1 Laboratório de Cartografia Digital - CTUFES Poligonação ou Caminhamento 2 A6 3 A6 Poligonação ou Caminhamento Este processo
Sistema Internacional de unidades (SI). 22/06/1799 sistema métrico na França
 CURSO DE ENGENHARIA CARTOGRÁFICA Carlos Aurélio Nadal Doutor em Ciências Geodésicas Professor Titular do Departamento de Geomática - Setor de Ciências da Terra Sistema Internacional de unidades (SI). 22/06/1799
CURSO DE ENGENHARIA CARTOGRÁFICA Carlos Aurélio Nadal Doutor em Ciências Geodésicas Professor Titular do Departamento de Geomática - Setor de Ciências da Terra Sistema Internacional de unidades (SI). 22/06/1799
x d z θ i Figura 2.1: Geometria das placas paralelas (Vista Superior).
 2 Lentes Metálicas Este capítulo destina-se a apresentar os princípios básicos de funcionamento e dimensionamento de lentes metálicas. Apresenta, ainda, comparações com as lentes dielétricas, cujas técnicas
2 Lentes Metálicas Este capítulo destina-se a apresentar os princípios básicos de funcionamento e dimensionamento de lentes metálicas. Apresenta, ainda, comparações com as lentes dielétricas, cujas técnicas
muito como cartas náuticas faça para o watercraft, ou o a mapa rodoviário para excitadores. Usando estas cartas e outras ferramentas pilotos possa
 Carta Aeronáutica é a mapa projetou ajudar dentro navegação de avião, muito como cartas náuticas faça para o watercraft, ou o a mapa rodoviário para excitadores. Usando estas cartas e outras ferramentas
Carta Aeronáutica é a mapa projetou ajudar dentro navegação de avião, muito como cartas náuticas faça para o watercraft, ou o a mapa rodoviário para excitadores. Usando estas cartas e outras ferramentas
"SISTEMAS DE COTAGEM"
 AULA 6T "SISTEMAS DE COTAGEM" Embora não existam regras fixas de cotagem, a escolha da maneira de dispor as cotas no desenho técnico depende de alguns critérios. A cotagem do desenho técnico deve tornar
AULA 6T "SISTEMAS DE COTAGEM" Embora não existam regras fixas de cotagem, a escolha da maneira de dispor as cotas no desenho técnico depende de alguns critérios. A cotagem do desenho técnico deve tornar
REPRESENTAÇÃO DE SISTEMAS DE POTÊNCIA
 1 REPRESENTAÇÃO DE SISTEMAS DE POTÊNCIA revisão mar06 1 - Introdução A maioria dos sistemas elétricos de potência é em corrente alternada. As instalações em corrente contínua são raras e tem aplicações
1 REPRESENTAÇÃO DE SISTEMAS DE POTÊNCIA revisão mar06 1 - Introdução A maioria dos sistemas elétricos de potência é em corrente alternada. As instalações em corrente contínua são raras e tem aplicações
Topografia Aula 2 Unidades Usuais e Revisão de Trigonometria
 Topografia Aula 2 Unidades Usuais e Revisão de Trigonometria Agronomia / Arquitetura e Urbanismo / Engenharia Civil Prof. Luiz Miguel de Barros luizmiguel.barros@yahoo.com.br Revisão Aula 1 O que é topografia?
Topografia Aula 2 Unidades Usuais e Revisão de Trigonometria Agronomia / Arquitetura e Urbanismo / Engenharia Civil Prof. Luiz Miguel de Barros luizmiguel.barros@yahoo.com.br Revisão Aula 1 O que é topografia?
7. DIAGRAMAÇÃO DAS PLACAS
 7. DIAGRAMAÇÃO DAS PLACAS A diagramação das placas de Sinalização Vertical de Indicação compreende os seguintes passos: Definição da altura das letras, a partir da velocidade regulamentada na via; Dimensionamento
7. DIAGRAMAÇÃO DAS PLACAS A diagramação das placas de Sinalização Vertical de Indicação compreende os seguintes passos: Definição da altura das letras, a partir da velocidade regulamentada na via; Dimensionamento
Mecânica dos Fluidos. Unidade 1- Propriedades Básicas dos Fluidos
 Mecânica dos Fluidos Unidade 1- Propriedades Básicas dos Fluidos Quais as diferenças fundamentais entre fluido e sólido? Fluido é mole e deformável Sólido é duro e muito Sólido é duro e muito pouco deformável
Mecânica dos Fluidos Unidade 1- Propriedades Básicas dos Fluidos Quais as diferenças fundamentais entre fluido e sólido? Fluido é mole e deformável Sólido é duro e muito Sólido é duro e muito pouco deformável
PROGRAMA DE INTEGRAÇÃO E CAPACITAÇÃO DER/2008 TÓPICOS DE DE PROJETO GEOMÉTRICO RODOVIÁRIO. Lucas Bach Adada
 PROGRAMA DE INTEGRAÇÃO E CAPACITAÇÃO DER/2008 TÓPICOS DE DE PROJETO GEOMÉTRICO RODOVIÁRIO Lucas Bach Adada 1 Conteúdo Programático Definição de Projeto Geométrico; Classificação das Vias e Rodovias ; Critérios
PROGRAMA DE INTEGRAÇÃO E CAPACITAÇÃO DER/2008 TÓPICOS DE DE PROJETO GEOMÉTRICO RODOVIÁRIO Lucas Bach Adada 1 Conteúdo Programático Definição de Projeto Geométrico; Classificação das Vias e Rodovias ; Critérios
Aula 9 ESCALA GRÁFICA. Antônio Carlos Campos
 Aula 9 ESCALA GRÁFICA META Apresentar as formas de medição da proporcionalidade entre o mundo real e os mapas através das escalas gráficas. OBJETIVOS Ao final desta aula, o aluno deverá: estabelecer formas
Aula 9 ESCALA GRÁFICA META Apresentar as formas de medição da proporcionalidade entre o mundo real e os mapas através das escalas gráficas. OBJETIVOS Ao final desta aula, o aluno deverá: estabelecer formas
Método analítico para o traçado da polar de arrasto de aeronaves leves subsônicas aplicações para a competição Sae-Aerodesign
 SIMPÓSIO INTERNAIONA E IÊNIAS INTEGRAAS A UNAERP AMPUS GUARUJÁ Método analítico para o traçado da polar de arrasto de aeronaves leves subsônicas aplicações para a competição Sae-Aerodesign uiz Eduardo
SIMPÓSIO INTERNAIONA E IÊNIAS INTEGRAAS A UNAERP AMPUS GUARUJÁ Método analítico para o traçado da polar de arrasto de aeronaves leves subsônicas aplicações para a competição Sae-Aerodesign uiz Eduardo
ITA - 2004 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 ITA - 2004 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Considere as seguintes afirmações sobre o conjunto U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} I. U e n(u) = 10 III. 5 U e {5}
ITA - 2004 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Considere as seguintes afirmações sobre o conjunto U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} I. U e n(u) = 10 III. 5 U e {5}
Fresando engrenagens cilíndricas com dentes retos
 Fresando engrenagens cilíndricas com dentes retos A UU L AL A Na aula passada você viu como furar na fresadora, utilizando a mesa divisora. Nesta aula você vai aprender a fresar engrenagens, utilizando
Fresando engrenagens cilíndricas com dentes retos A UU L AL A Na aula passada você viu como furar na fresadora, utilizando a mesa divisora. Nesta aula você vai aprender a fresar engrenagens, utilizando
TOPOGRAFIA - Planimetria. Alex Mota dos Santos
 TOPOGRAFIA - Planimetria Alex Mota dos Santos Unidades de Medida Linear polegada = 2,75 cm = 0,0275 m polegada inglesa = 2,54 cm = 0,0254 m pé = 30,48cm = 0,3048 m jarda = 91,44cm = 0,9144m milha brasileira
TOPOGRAFIA - Planimetria Alex Mota dos Santos Unidades de Medida Linear polegada = 2,75 cm = 0,0275 m polegada inglesa = 2,54 cm = 0,0254 m pé = 30,48cm = 0,3048 m jarda = 91,44cm = 0,9144m milha brasileira
Instituto Superior de Engenharia do Porto Departamento de Engenharia Electrotécnica. Licenciatura em Engenharia Electrotécnica e de Computadores
 Instituto Superior de Engenharia do Porto Departamento de Engenharia Electrotécnica Licenciatura em Engenharia Electrotécnica e de Computadores SISEL - Sistemas Electromecânicos Eercícios de 006 . Considere
Instituto Superior de Engenharia do Porto Departamento de Engenharia Electrotécnica Licenciatura em Engenharia Electrotécnica e de Computadores SISEL - Sistemas Electromecânicos Eercícios de 006 . Considere
UNIDADE II Processos de medição de ângulos e distâncias.
 FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS - FESO CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS UNIFESO CENTRO DE CIÊNCIAS E TECNOLOGIA CCT CURSO DE ENGENHARIA AMBIENTAL Profª Drª Verônica Rocha Bonfim Engª Florestal
FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS - FESO CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS UNIFESO CENTRO DE CIÊNCIAS E TECNOLOGIA CCT CURSO DE ENGENHARIA AMBIENTAL Profª Drª Verônica Rocha Bonfim Engª Florestal
Capítulo 2 CINEMÁTICA
 Capítulo CINEMÁTICA DISCIPLINA DE FÍSICA CAPÍTULO - CINEMÁTICA.1 Uma partícula com movimento rectilíneo desloca-se segundo a seguinte equação: x = 0,5 t.1.1 Desenhe o gráfico da função r(t), no intervalo
Capítulo CINEMÁTICA DISCIPLINA DE FÍSICA CAPÍTULO - CINEMÁTICA.1 Uma partícula com movimento rectilíneo desloca-se segundo a seguinte equação: x = 0,5 t.1.1 Desenhe o gráfico da função r(t), no intervalo
6. Erosão. Início do transporte sólido por arrastamento
 6. Erosão. Início do transporte sólido por arrastamento 6.1. Introdução A erosão consiste na remoção do material do leito pelas forças de arrastamento que o escoamento provoca. O oposto designa-se por
6. Erosão. Início do transporte sólido por arrastamento 6.1. Introdução A erosão consiste na remoção do material do leito pelas forças de arrastamento que o escoamento provoca. O oposto designa-se por
Gráficos Cinemáticos (2) v (m/s) (1)
 Gráficos Cinemáticos 1- Na figura estão representados os diagramas de velocidade de dois móveis em função do tempo. Esses móveis partem de um mesmo ponto, a partir do repouso, e percorrem a mesma trajetória
Gráficos Cinemáticos 1- Na figura estão representados os diagramas de velocidade de dois móveis em função do tempo. Esses móveis partem de um mesmo ponto, a partir do repouso, e percorrem a mesma trajetória
MAGNETISMO - ELETROMAGNETISMO
 MAGNETISMO - ELETROMAGNETISMO MAGNETISMO Estuda os corpos que apresentam a propriedade de atrair o ferro. Estes corpos são denominados imãs ou magnetos. Quando suspendemos um imã deixando que ele gire
MAGNETISMO - ELETROMAGNETISMO MAGNETISMO Estuda os corpos que apresentam a propriedade de atrair o ferro. Estes corpos são denominados imãs ou magnetos. Quando suspendemos um imã deixando que ele gire
PROCESSO SELETIVO DO PRIMEIRO SEMESTRE DE 2015 PROVA DE PROCESSOS DE TRANSFORMAÇÃO METAL-MECÂNICA
 PROVA DE PROCESSOS DE TRANSFORMAÇÃO METAL-MECÂNICA Um metal deforma-se plasticamente segundo a curva Y = 400 + 700 e 0,4. Deseja-se trefilar um fio circular deste metal do diâmetro inicial 8 mm, promovendo
PROVA DE PROCESSOS DE TRANSFORMAÇÃO METAL-MECÂNICA Um metal deforma-se plasticamente segundo a curva Y = 400 + 700 e 0,4. Deseja-se trefilar um fio circular deste metal do diâmetro inicial 8 mm, promovendo
Levantamento topográfico
 MA092 - Geometria plana e analítica - Segundo projeto Levantamento topográfico Francisco A. M. Gomes Outubro de 2014 1 Descrição do projeto Nessa atividade, vamos usar a lei dos senos e a lei dos cossenos
MA092 - Geometria plana e analítica - Segundo projeto Levantamento topográfico Francisco A. M. Gomes Outubro de 2014 1 Descrição do projeto Nessa atividade, vamos usar a lei dos senos e a lei dos cossenos
Palavras-Chave: Sistema de Posicionamento Global. Sistemas de Localização Espacial. Equação de Superfícies Esféricas.
 METODOS MATEMÁTICOS PARA DEFINIÇÃO DE POSICIONAMENTO Alberto Moi 1 Rodrigo Couto Moreira¹ Resumo Marina Geremia¹ O GPS é uma tecnologia cada vez mais presente em nossas vidas, sendo que são inúmeras as
METODOS MATEMÁTICOS PARA DEFINIÇÃO DE POSICIONAMENTO Alberto Moi 1 Rodrigo Couto Moreira¹ Resumo Marina Geremia¹ O GPS é uma tecnologia cada vez mais presente em nossas vidas, sendo que são inúmeras as
4. A FUNÇÃO AFIM. Uma função f: R R chama-se afim quando existem números reais a e b tais que f(x) = ax + b para todo x R. Casos particulares
 38 4. A FUNÇÃO AFIM Uma função f: R R chama-se afim quando existem números reais a e b tais que f(x) = ax + b para todo x R. Casos particulares 1) A função identidade fr : Rdefinida por f(x) = x para todo
38 4. A FUNÇÃO AFIM Uma função f: R R chama-se afim quando existem números reais a e b tais que f(x) = ax + b para todo x R. Casos particulares 1) A função identidade fr : Rdefinida por f(x) = x para todo
-ESTRUTURA VIÁRIA TT048 CURVAS HORIZONTAIS DE TRANSIÇÃO
 INFRAINFRA -ESTRUTURA VIÁRIA TT048 CURVAS HORIZONTAIS DE TRANSIÇÃO Prof.Djalma Prof.Djalma Pereira Prof. Eduardo Ratton Profa. Profa.Gilza Fernandes Blasi Profa. Profa. Márcia de Andrade Pereira CURVAS
INFRAINFRA -ESTRUTURA VIÁRIA TT048 CURVAS HORIZONTAIS DE TRANSIÇÃO Prof.Djalma Prof.Djalma Pereira Prof. Eduardo Ratton Profa. Profa.Gilza Fernandes Blasi Profa. Profa. Márcia de Andrade Pereira CURVAS
2) A área da parte mostarda dos 100 padrões é 6. 9. 2. 3) A área total bordada com a cor mostarda é (5400 + 3700) cm 2 = 9100 cm 2
 MATEMÁTICA 1 Um tapete deve ser bordado sobre uma tela de m por m, com as cores marrom, mostarda, verde e laranja, da seguinte forma: o padrão quadrado de 18 cm por 18 cm, mostrado abaio, será repetido
MATEMÁTICA 1 Um tapete deve ser bordado sobre uma tela de m por m, com as cores marrom, mostarda, verde e laranja, da seguinte forma: o padrão quadrado de 18 cm por 18 cm, mostrado abaio, será repetido
Topografia. Conceitos Básicos. Prof.: Alexandre Villaça Diniz - 2004-
 Topografia Conceitos Básicos Prof.: Alexandre Villaça Diniz - 2004- 1 ÍNDICE ÍNDICE...1 CAPÍTULO 1 - Conceitos Básicos...2 1. Definição...2 1.1 - A Planta Topográfica...2 1.2 - A Locação da Obra...4 2.
Topografia Conceitos Básicos Prof.: Alexandre Villaça Diniz - 2004- 1 ÍNDICE ÍNDICE...1 CAPÍTULO 1 - Conceitos Básicos...2 1. Definição...2 1.1 - A Planta Topográfica...2 1.2 - A Locação da Obra...4 2.
Facear Concreto Estrutural I
 1. ASSUNTOS DA AULA a) Concreto: Definição e requisitos de norma b) Concreto: Massa específica, resistência a compressão, resistência a tração e módulo de elasticidade c) Coeficiente de Poisson d) Diagrama
1. ASSUNTOS DA AULA a) Concreto: Definição e requisitos de norma b) Concreto: Massa específica, resistência a compressão, resistência a tração e módulo de elasticidade c) Coeficiente de Poisson d) Diagrama
1 SISTEMAS DE COORDENADAS
 1 SISTEMAS DE COORDENADAS 1.1 Objetivos do capítulo Aonaldestecapítulooalunodeverá: Representar pontos em coordenadas polares, cilíndricas e esféricas; Representargracamentecurvasescritasemcoordenadaspolares;
1 SISTEMAS DE COORDENADAS 1.1 Objetivos do capítulo Aonaldestecapítulooalunodeverá: Representar pontos em coordenadas polares, cilíndricas e esféricas; Representargracamentecurvasescritasemcoordenadaspolares;
CAPÍTULO. Casuística
 Casuística CAPÍTULO IV Todos os casos abordados neste capítulo são propostos para esclarecer de que maneira são calculadas as velocidades nas colisões entre dois veículos. Por se tratarem de eventos reais,
Casuística CAPÍTULO IV Todos os casos abordados neste capítulo são propostos para esclarecer de que maneira são calculadas as velocidades nas colisões entre dois veículos. Por se tratarem de eventos reais,
MATEMÁTICA A - 12o Ano N o s Complexos - Equações e problemas
 MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Exercícios de exames e testes intermédios 1. Em C, conjunto dos números complexos, considere z = + i19 cis θ Determine os valores de θ pertencentes
MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Exercícios de exames e testes intermédios 1. Em C, conjunto dos números complexos, considere z = + i19 cis θ Determine os valores de θ pertencentes
Exercícios 3 Movimentos em 2 Dimensões, Movimento Circular e Aplicações
 Exercícios 3 Movimentos em 2 Dimensões, Movimento Circular e Aplicações Movimentos em 2D 1) Você está operando um modelo de carro com controle remoto em um campo de tênis vazio. Sua posição é a origem
Exercícios 3 Movimentos em 2 Dimensões, Movimento Circular e Aplicações Movimentos em 2D 1) Você está operando um modelo de carro com controle remoto em um campo de tênis vazio. Sua posição é a origem
Vestibulando Web Page www.vestibulandoweb.com.br
 1. (Ufv 2000) Um aluno, sentado na carteira da sala, observa os colegas, também sentados nas respectivas carteiras, bem como um mosquito que voa perseguindo o professor que fiscaliza a prova da turma.
1. (Ufv 2000) Um aluno, sentado na carteira da sala, observa os colegas, também sentados nas respectivas carteiras, bem como um mosquito que voa perseguindo o professor que fiscaliza a prova da turma.
Cálculo da carga aplicada
 508-BR O guia linear é capaz de receber cargas e momentos em todas as direções que sejam gerados em função da posição de montagem, do alinhamento, da posição do centro de gravidade de um objeto móvel,
508-BR O guia linear é capaz de receber cargas e momentos em todas as direções que sejam gerados em função da posição de montagem, do alinhamento, da posição do centro de gravidade de um objeto móvel,
Olimpíada Brasileira de Física 2001 2ª Fase
 Olimpíada Brasileira de Física 2001 2ª Fase Gabarito dos Exames para o 1º e 2º Anos 1ª QUESTÃO Movimento Retilíneo Uniforme Em um MRU a posição s(t) do móvel é dada por s(t) = s 0 + vt, onde s 0 é a posição
Olimpíada Brasileira de Física 2001 2ª Fase Gabarito dos Exames para o 1º e 2º Anos 1ª QUESTÃO Movimento Retilíneo Uniforme Em um MRU a posição s(t) do móvel é dada por s(t) = s 0 + vt, onde s 0 é a posição
PROVA DE CONHECIMENTOS ESPECÍFICOS
 10 PROVA DE CONHECIMENTOS ESPECÍFICOS QUESTÃO 31 As projeções do lado do polígono, com rumo no 4 o quadrante, sobre os eixos x e y são, respectivamente: a) positiva e positiva b) positiva e negativa c)
10 PROVA DE CONHECIMENTOS ESPECÍFICOS QUESTÃO 31 As projeções do lado do polígono, com rumo no 4 o quadrante, sobre os eixos x e y são, respectivamente: a) positiva e positiva b) positiva e negativa c)
O que é o Sistema Geodésico de Referência? Qual é o Sistema Geodésico adotado no Brasil? Qual a diferença entre o Sistema SAD69 e SIRGAS2000?
 O que é o Sistema Geodésico de Referência? É um sistema coordenado que serve de referência ao posicionamento no globo terrestre ou em um território nacional ou continental, utilizado para representar características
O que é o Sistema Geodésico de Referência? É um sistema coordenado que serve de referência ao posicionamento no globo terrestre ou em um território nacional ou continental, utilizado para representar características
- PROVA OBJETIVA - Câmpus Santos Dumont - Edital 005/2014
 MINISTÉRIO DA EDUCAÇÃO INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO SUDESTE DE MINAS GERAIS CONCURSO PÚBLICO PARA PROVIMENTO DE CARGO EFETIVO DE DOCENTES ÁREA: Matemática - PROVA OBJETIVA - Câmpus
MINISTÉRIO DA EDUCAÇÃO INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO SUDESTE DE MINAS GERAIS CONCURSO PÚBLICO PARA PROVIMENTO DE CARGO EFETIVO DE DOCENTES ÁREA: Matemática - PROVA OBJETIVA - Câmpus
PUCGoiás Física I. Lilian R. Rios. Rotação
 PUCGoiás Física I Lilian R. Rios Rotação O movimento de um cd, de um ventilador de teto, de uma roda gigante, entre outros, não podem ser representados como o movimento de um ponto cada um deles envolve
PUCGoiás Física I Lilian R. Rios Rotação O movimento de um cd, de um ventilador de teto, de uma roda gigante, entre outros, não podem ser representados como o movimento de um ponto cada um deles envolve
Aula -2 Motores de Corrente Contínua com Escovas
 Aula -2 Motores de Corrente Contínua com Escovas Introdução Será descrito neste tópico um tipo específico de motor que será denominado de motor de corrente contínua com escovas. Estes motores possuem dois
Aula -2 Motores de Corrente Contínua com Escovas Introdução Será descrito neste tópico um tipo específico de motor que será denominado de motor de corrente contínua com escovas. Estes motores possuem dois
(Testes intermédios e exames 2005/2006)
 158. Indique o conjunto dos números reais que são soluções da inequação log 3 (1 ) 1 (A) [,1[ (B) [ 1,[ (C) ], ] (D) [, [ 159. Na figura abaio estão representadas, em referencial o. n. Oy: parte do gráfico
158. Indique o conjunto dos números reais que são soluções da inequação log 3 (1 ) 1 (A) [,1[ (B) [ 1,[ (C) ], ] (D) [, [ 159. Na figura abaio estão representadas, em referencial o. n. Oy: parte do gráfico
Esforços axiais e tensões normais
 Esforços axiais e tensões normais (Ref.: Beer & Johnston, Resistência dos Materiais, ª ed., Makron) Considere a estrutura abaixo, construída em barras de aço AB e BC, unidas por ligações articuladas nas
Esforços axiais e tensões normais (Ref.: Beer & Johnston, Resistência dos Materiais, ª ed., Makron) Considere a estrutura abaixo, construída em barras de aço AB e BC, unidas por ligações articuladas nas
Aula 5 - Parte 1: Funções. Exercícios Propostos
 Aula 5 - Parte 1: Funções Exercícios Propostos 1 Construção de Funções: a) Um grupo de amigos deseja alugar uma van, por um dia, para um passeio, ao custo de R$300,00. Um levantamento preliminar indicou
Aula 5 - Parte 1: Funções Exercícios Propostos 1 Construção de Funções: a) Um grupo de amigos deseja alugar uma van, por um dia, para um passeio, ao custo de R$300,00. Um levantamento preliminar indicou
