DE EXERCÍCIOS DE VARIÁVEIS COMPLEXAS
|
|
|
- Anderson Farinha Aldeia
- 8 Há anos
- Visualizações:
Transcrição
1 Cálculo Avançado A - Variávis Complas LISTA DE EXERCÍCIOS DE VARIÁVEIS COMPLEXAS ) Encontr todas as singularidads das funçõs abaio, aprsntando-as m forma algébrica: a) f ( ) sc() b) j 5 + j f () ( j) j c) f ( ) cot gh( j + ) f ( ) cosh + snh ) f ( ) f) f ( ) snh ( ) + cosh( ) sn ( ) ( ) f h) f ( ) + j cosh + snh i) f ( ) j) f ( ) k) f ( ) m) f () + 5 cosh( ) + f ( ) f ( ) + ( )( ) o) f ( ) f ( ) + ( j) j 8 q) f () cosh( ) cosh( ) + r) f () ( 5 ) sn + 6j 6 sn ( / ) 6 ( + 6) ( / ) sn cos 5 + ( + ) j cos ) Dtrmin todas singularidads das funçõs abaio classifiqu cada singularidad como rmovívl, pólo d uma dada ordm ou ssncial: a) b) cos() f () sn( + ) f () ( + j) ( j) ) sn( ) f () f () ( ) cos ( ) ( + ) h) j f () + sn( ) f () snh( ) / c) f () ( + j) f) f () ( + ) i) f ()
2 Cálculo Avançado A - Variávis Complas j) f () tg() k) m) f () cos() /(( + )) f () j f () o) sn( ) f () f () ( )( j) ( + ) snh( ) f () q) f () cosh () r) f () j + ( ) sn() s) f () + ( ) t) f () cos sc () ) Encontr a part ral imaginária das funçõs f() abaio, usando as Equaçõs d Cauch-Rimann, dtrmin todos os pontos do plano complo nos quais a função é drivávl, calculando sua drivada: a) f () j b) f () j c) f () ) f () + f () j f) f () + Im( ) f () R() h) f () 8 + f () i) ( ) j) f () j + k) f () + f () j + j m) f () R() Im( ) f () j o) f () Im + f () ) Vrifiqu s as funçõs do problma acima são analíticas ou, caso contrário, indiqu as singularidads da função f() 5) Nas qustõs a sguir, calcul a intgral ( ) Obsrv qu todos os caminhos fchados são positivamnt orintados: a) f (), ond C é qualqur caminho fchado ao rdor d j j sn( ) b) f (), ond C é a circunfrência 5 f d para a função o caminho dados C c) f () 5 + j, ond C é a circunfrência + j
3 Cálculo Avançado A - Variávis Complas ) f) f () f () f (), ond C é o rtângulo d vértics ± ± j ( ) j, ond C é a circunfrência ( + j) cos( j) ( + j), ond C é qualqur caminho fchado ao rdor d j f ( ) h) f ( ), ond C é a circunfrência j + ( + j) sn( ), ond C é qualqur caminho fchado ao rdor d ( + ) i) f ( ) R( + ), ond C é o sgmnto d rta d + j até 5j j) f () + j, ond C é o sgmnto d rta d 0 até j k) f ( ) () Im( j) m) o), ond C é o quadrado d vértics 0,, + j j f, ond C é a circunfrência unitária cntrada na origm f () f () f () ( snh ( ) ) cosh, ond C é um caminho fchado ao rdor d + cos( ) ( + j), ond C é o triângulo d vértics 0, 8j 8j sn( ) ( + j) cos(), ond C é a circunfrência d raio cntrada na origm f (), ond C é a circunfrência d raio cntro j ( + j) 6) Calcul as intgrais m cada um dos problmas até 6, considrando qu todos os caminhos fchados são orintados positivamnt: a) + C ( ) ( + j) d, ond C é a circunfrência d raio cntro j cos( ) b) d, ond C é o quadrado d lados parallos aos ios, mdindo, cntrado m j C +
4 Cálculo Avançado A - Variávis Complas c) C d, ond C é a circunfrência d raio cntro j j d, ond C é a circunfrência d raio cntrada na origm C + j ) d, ond C é a circunfrência d raio cntrada na origm C + 6 cos( ) f) d, ond C é a circunfrência d raio / cntro j/8 C ( + 9) C j d, ond C é a circunfrência d raio cntrada m j ( j) 8 j+ h) d, ond C é a circunfrência d raio, cntrada m j C + j i) d, ond C é qualqur caminho fchado ao rdor d C ( ) j) C ( j) d, ond C é qualqur caminho fchado ao rdor d 0 j sn() cos() k) d, ond C é a circunfrência d raio cntrada na origm C + cosh() C ( 9) d, ond C é qualqur caminho fchado ao rdor d 0 qu não contnha o m) d, ond C é a circunfrência j C d, ond C é a circunfrência 5 C + j o) q) ( j) d C + ( + ) cosh( ) ( j)( j) C + ( + j), ond C é a circunfrência 8 d, ond C é a circunfrência j C d, ond C é a circunfrência j
5 Cálculo Avançado A - Variávis Complas r) cos C ( j) ( + )( ) d, ond C é a circunfrência + j 7) Sndo C o círculo + j, orintado positivamnt, dfin-s a função: j F (, ) d C ( ) ( ) Calcul F(j, -j), F(j, -5j) F(-j, j) 8) Sndo C o círculo, orintado positivamnt, dfin-s a função: j F ( ω, N) d C N ( ω) Calcul F(, ), F(, ) F(0, 5) RESPOSTAS: ) a) + k ou + k + jln 5 ; b) 0, ± j, ± ; c) k + j; 0,, ± j,, ± j ; k k ) ln + j + ; f) j, ± j ; j + ; 8 h), ± j,, ± j ; i) l n + k j ; j) ± j, ± j, ± j ; k) + jk ; ; m) ±, ± ; 0, ( ± j), ( ± j), ± j k j + ; o) j, ± j, + ± ; ( ± ± j) ; k + ln q) ln 5 + j ; r) + jk ) a) Pólo d ordm m 0 b) Pólo duplo m -j; pólo simpls m j c) Singularidad ssncial m 0 Singularidad rmovívl m ) Pólos simpls m j j; pólo duplo m f) Pólo duplo m - Singularidad rmovívl m j, pólo simpls m -j 5
6 Cálculo Avançado A - Variávis Complas h) Pólo simpls m nj, para todo n 0 intiro; singularidad rmovívl m 0 i) Pólos simpls m, -, j -j j) Pólos simpls m ( n + ) 6, para todo intiro n k) Pólos simpls m ( n + ), para todo intiro n Singularidad ssncial m 0 - m) Pólo d ordm m 0 Singularidad rmovívl m 0 ; pólo duplo m j o) Pólo d ordm m - Pólo triplo m 0 q) Nnhuma singularidad r) Pólo duplo m - n s) Pólo simpls m - t) Pólos triplos m, para todo intiro n ) a) u(, ), v(, ) ; m todo complo; f () b) u(, ), v(, ) ; m todo complo; f () j c) u(, ), v(, ) 0; m nnhum ponto do plano complo ) u(, ) +, v(, ) ; m todo complo não nulo; u (, ) 0, v(, ) ; m 0; f (0) 0 f) u (, ), v(, ) ; m nnhum ponto do plano complo u (, ), v(, ) ; m nnhum ponto do plano complo f () h) u(, ) 8 +, v(, ) 8 ; m todo complo; f () 8 i) u(, ), v(, ) ; m 0; f (0) 0 j) u(, ), v(, ) ; m nnhum ponto do plano complo k) u(, ) u(, ) +, v(, ) ; m todo complo 0, + ( + ) ; f () j v(, ) ; m todo complo j; f () + ( + ) + j m) u (, ), v(, ) 0 ; m nnhum ponto do plano complo u (, ) 6, v(, ) + 6 ; m todo complo; f () 6j o) u(, ), v(, ) 0 ; m nnhum ponto do plano complo ( + ) + u(, ), v(, ) ; m nnhum ponto do plano complo ( ) ) As funçõs dos problmas b, h n são analíticas As funçõs dos problmas c,, f, g, j, m, o p possum singularidads m todos os pontos do plano complo As funçõs dos problmas d k possum uma singularidad m 0 A função do problma l possui uma singularidad m j
7 Cálculo Avançado A - Variávis Complas 5) a) j b) j c) ( ) 8j ) [ cos() jsn() ] f) j cosh() j 6) a) j b) cosh( ) c) 0 j/ ( ) ) j f) j j 7) F(j, -j) j [ cosh( ) + ] h) 5( j) cos( 56) i) 9 j j) 0 k) 0 j m) j cosh(snh( )) h) 0 i) j 8j j) [ ] k) jsnh() cosh( ) j [ cosh( 9) ] 9 8 m) j, F(j, -5j) 0 F(-j, j) 8) F(, ) j, F(, ) 8 j F(0, 5) 0 9 j 8-9snh() j cos + jsn o) [ snh ( ) + j cosh( ) ] [ ( ) ( )] 0 + j o) ( ) 0 q) 0 r) [ cos( ) + j] 7
01.Resolva as seguintes integrais:
 INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA MAT A CÁLCULO A a LISTA DE EXERCÍCIOS Atualizada m 7..Rsolva as sguints intgrais: 5.).).).) sn().5) sn cos.) tg 5 sc.7).8).9) ln 5.) arctg.).).).).7)
INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA MAT A CÁLCULO A a LISTA DE EXERCÍCIOS Atualizada m 7..Rsolva as sguints intgrais: 5.).).).) sn().5) sn cos.) tg 5 sc.7).8).9) ln 5.) arctg.).).).).7)
Resolução. Admitindo x = x. I) Ax = b
 Considr uma população d igual númro d homns mulhrs, m qu sjam daltônicos % dos homns 0,% das mulhrs. Indiqu a probabilidad d qu sja mulhr uma pssoa daltônica slcionada ao acaso nssa população. a) b) c)
Considr uma população d igual númro d homns mulhrs, m qu sjam daltônicos % dos homns 0,% das mulhrs. Indiqu a probabilidad d qu sja mulhr uma pssoa daltônica slcionada ao acaso nssa população. a) b) c)
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 2. < arg z < π}.
 Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR LOGARITMOS E INTEGRAÇÃO DE FUNÇÕES COMPLEXAS Logaritmos () Para cada um dos sguints conjuntos
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR LOGARITMOS E INTEGRAÇÃO DE FUNÇÕES COMPLEXAS Logaritmos () Para cada um dos sguints conjuntos
Função Exponencial: Conforme já vimos, o candidato natural à função exponencial complexa é dado pela função. f z x iy f z e cos y ie sen y.
 Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Curso de Pré Cálculo Dif. Int. I Aula 11 Ministrante Profª. Drª. Danielle Durski Figueiredo Material elaborado pelo Programa de Pré-Cálculo da
 Curso d Pré Cálculo Dif. Int. I Aula Ministrant Profª. Drª. Danill Durski Figuirdo Matrial laborado plo Programa d Pré-Cálculo da Macknzi http://www.macknzi.br/filadmin/graduacao/ee/arquivos/calculo_zro/trigonomtria.pdf
Curso d Pré Cálculo Dif. Int. I Aula Ministrant Profª. Drª. Danill Durski Figuirdo Matrial laborado plo Programa d Pré-Cálculo da Macknzi http://www.macknzi.br/filadmin/graduacao/ee/arquivos/calculo_zro/trigonomtria.pdf
UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO
 UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO 0 Nos rcícios a) ), ncontr a drivada da função dada, usando a dfinição a) f ( ) + b) f ( ) c) f ( ) 5 d) f ( )
UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO 0 Nos rcícios a) ), ncontr a drivada da função dada, usando a dfinição a) f ( ) + b) f ( ) c) f ( ) 5 d) f ( )
tg 2 x , x > 0 Para determinar a continuidade de f em x = 0, devemos calcular os limites laterais
 UFRGS Instituto d Matmática DMPA - Dpto. d Matmática Pura Aplicada MAT 0 353 Cálculo Gomtria Analítica I A Gabarito da a PROVA fila A 5 d novmbro d 005 Qustão (,5 pontos Vrifiqu s a função f dada abaixo
UFRGS Instituto d Matmática DMPA - Dpto. d Matmática Pura Aplicada MAT 0 353 Cálculo Gomtria Analítica I A Gabarito da a PROVA fila A 5 d novmbro d 005 Qustão (,5 pontos Vrifiqu s a função f dada abaixo
Derivada Escola Naval
 Drivada Escola Naval EN A drivada f () da função f () = l og é: l n (B) 0 l n (E) / l n EN S tm-s qu: f () = s s 0 s < < 0 s < I - f () só não é drivávl para =, = 0 = II - f () só não é contínua para =
Drivada Escola Naval EN A drivada f () da função f () = l og é: l n (B) 0 l n (E) / l n EN S tm-s qu: f () = s s 0 s < < 0 s < I - f () só não é drivávl para =, = 0 = II - f () só não é contínua para =
5.10 EXERCÍCIO pg. 215
 EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção
EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção
Análise Matemática IV Problemas para as Aulas Práticas
 Anális Matmática IV Problmas para as Aulas Práticas 7 d Abril d 003 Smana 1. Us as quaçõs d cauchy-rimann para dtrminar o conjunto dos pontos do plano complo ond as sguints funçõs admitm drivada calcul
Anális Matmática IV Problmas para as Aulas Práticas 7 d Abril d 003 Smana 1. Us as quaçõs d cauchy-rimann para dtrminar o conjunto dos pontos do plano complo ond as sguints funçõs admitm drivada calcul
Lista 5: Regras de Derivação
 Univrsidad Fdral do Val do São Francisco Câmpus Juaziro BA Colgiado d Engnharia Elétrica Prof. Pdro Macário d Moura Cálculo Difrncial Intgral Lista : Rgras d Drivação 0. Calcular as drivadas das prssõs
Univrsidad Fdral do Val do São Francisco Câmpus Juaziro BA Colgiado d Engnharia Elétrica Prof. Pdro Macário d Moura Cálculo Difrncial Intgral Lista : Rgras d Drivação 0. Calcular as drivadas das prssõs
INSTITUTO FEDERAL DA BAHIA CAMPUS JEQUIÉ LISTA DE EXERCÍCIOS DE MATEMÁTICA ALUNO:
 INSTITUTO FEDERAL DA BAHIA CAMPUS JEQUIÉ LISTA DE EXERCÍCIOS DE MATEMÁTICA ALUNO: LISTA Ciclo trigonométrico, rdução d arcos, quaçõs trigonométricas - (UFJF MG) Escrvndo os númros rais x, y, w, z y, x,
INSTITUTO FEDERAL DA BAHIA CAMPUS JEQUIÉ LISTA DE EXERCÍCIOS DE MATEMÁTICA ALUNO: LISTA Ciclo trigonométrico, rdução d arcos, quaçõs trigonométricas - (UFJF MG) Escrvndo os númros rais x, y, w, z y, x,
1.1 O Círculo Trigonométrico
 Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
2 x. ydydx. dydx 1)INTEGRAIS DUPLAS: RESUMO. , sendo R a região que. Exemplo 5. Calcule integral dupla. xda, no retângulo
 Intgração Múltipla Prof. M.Sc. Armando Paulo da Silva UTFP Campus Cornélio Procópio )INTEGAIS DUPLAS: ESUMO Emplo Emplo Calcul 6 Calcul 6 dd dd O fato das intgrais rsolvidas nos mplos srm iguais Não é
Intgração Múltipla Prof. M.Sc. Armando Paulo da Silva UTFP Campus Cornélio Procópio )INTEGAIS DUPLAS: ESUMO Emplo Emplo Calcul 6 Calcul 6 dd dd O fato das intgrais rsolvidas nos mplos srm iguais Não é
Cálculo Diferencial II Lista de Exercícios 1
 Cálculo Difrncil II List d Ercícios 1 CONJUNTO ABERTO E PONTOS DE ACUMULAÇÃO 1 Vrifiqu quis dos conjuntos sguir são brtos m (, ) 1 (, ) 0 (, ) 0 (, ) 0 1 Dtrmin o conjunto d pontos d cumulção do conjunto
Cálculo Difrncil II List d Ercícios 1 CONJUNTO ABERTO E PONTOS DE ACUMULAÇÃO 1 Vrifiqu quis dos conjuntos sguir são brtos m (, ) 1 (, ) 0 (, ) 0 (, ) 0 1 Dtrmin o conjunto d pontos d cumulção do conjunto
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática
 Univrsidad Fdral do Rio d Janiro Instituto d Matmática Dpartamnto d Matmática Gabarito da Prova Final d Cálculo Difrncial Intgral II - 07-I (MAC 8 - IQN+IFN+Mto, 6/06/07 Qustão : (.5 pontos Rsolva { xy.
Univrsidad Fdral do Rio d Janiro Instituto d Matmática Dpartamnto d Matmática Gabarito da Prova Final d Cálculo Difrncial Intgral II - 07-I (MAC 8 - IQN+IFN+Mto, 6/06/07 Qustão : (.5 pontos Rsolva { xy.
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT 013 - Matemática I Prof.: Leopoldina Cachoeira Menezes
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT - Mamáica I Prof.: Lopoldina Cachoira Mnzs Prof.: Mauricio Sobral Brandão ª Lisa d Ercícios Par I: Funçõs Econômicas
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT - Mamáica I Prof.: Lopoldina Cachoira Mnzs Prof.: Mauricio Sobral Brandão ª Lisa d Ercícios Par I: Funçõs Econômicas
2) A área da parte mostarda dos 100 padrões é 6. 9. 2. 3) A área total bordada com a cor mostarda é (5400 + 3700) cm 2 = 9100 cm 2
 MATEMÁTICA 1 Um tapete deve ser bordado sobre uma tela de m por m, com as cores marrom, mostarda, verde e laranja, da seguinte forma: o padrão quadrado de 18 cm por 18 cm, mostrado abaio, será repetido
MATEMÁTICA 1 Um tapete deve ser bordado sobre uma tela de m por m, com as cores marrom, mostarda, verde e laranja, da seguinte forma: o padrão quadrado de 18 cm por 18 cm, mostrado abaio, será repetido
Seja f uma função r.v.r. de domínio D e seja a R um ponto de acumulação de
 p-p8 : Continuidad d funçõs rais d variávl ral. Lr atntamnt. Dominar os concitos. Fazr rcícios. Função contínua, prolongávl por continuidad, dscontínua. Classificação d dscontinuidads. Continuidad num
p-p8 : Continuidad d funçõs rais d variávl ral. Lr atntamnt. Dominar os concitos. Fazr rcícios. Função contínua, prolongávl por continuidad, dscontínua. Classificação d dscontinuidads. Continuidad num
c) 0 0 x y na região R limitada pelas retas y 1,
 Univrsidad Fdral d Viçosa DEPATAMENTO DE MATEMÁTIA LISTA DE EXEÍIOS - MAT ÁLULO DIFEENIAL E INTEGAL III Intgrais alcul o valor das sguints intgrais rptidas LISTA DE EXEÍIOS INTEGAIS a) ( ) d d b) d d c)
Univrsidad Fdral d Viçosa DEPATAMENTO DE MATEMÁTIA LISTA DE EXEÍIOS - MAT ÁLULO DIFEENIAL E INTEGAL III Intgrais alcul o valor das sguints intgrais rptidas LISTA DE EXEÍIOS INTEGAIS a) ( ) d d b) d d c)
III Integrais Múltiplos
 INTITUTO POLITÉCNICO DE TOMA Escola uprior d Tcnologia d Tomar Ára Intrdpartamntal d Matmática Anális Matmática II III Intgrais Múltiplos. Calcul o valor dos sguints intgrais: a) d d ; (ol. /) b) d d ;
INTITUTO POLITÉCNICO DE TOMA Escola uprior d Tcnologia d Tomar Ára Intrdpartamntal d Matmática Anális Matmática II III Intgrais Múltiplos. Calcul o valor dos sguints intgrais: a) d d ; (ol. /) b) d d ;
10. EXERCÍCIOS (ITA-1969 a ITA-2001)
 . EXERCÍCIOS (ITA-969 a ITA-) - (ITA - 969) Sjam f() = + g() = duas funçõs rais d variávl ral. Então (gof)(y ) é igual a: a) y y + b) (y ) + c) y + y d) y y + ) y - (ITA -97) Sjam A um conjunto finito
. EXERCÍCIOS (ITA-969 a ITA-) - (ITA - 969) Sjam f() = + g() = duas funçõs rais d variávl ral. Então (gof)(y ) é igual a: a) y y + b) (y ) + c) y + y d) y y + ) y - (ITA -97) Sjam A um conjunto finito
Curso: Engenharia Industrial Elétrica. Análise de variáveis Complexas MAT 216 Turma: 01
 urso: Egharia Idustrial Elétrica Aális d variávis omplas MAT 6 Profssora: Edmary S B Araújo Turma: Lista d Provas Rspodu Jsus: Em vrdad, m vrdad t digo: qum ão ascr da água do Espírito ão pod trar o rio
urso: Egharia Idustrial Elétrica Aális d variávis omplas MAT 6 Profssora: Edmary S B Araújo Turma: Lista d Provas Rspodu Jsus: Em vrdad, m vrdad t digo: qum ão ascr da água do Espírito ão pod trar o rio
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA LIMITES E DERIVADAS MAT B Prof a Graça Luzia
 INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA LIMITES E DERIVADAS MAT B - 008. Prof a Graça Luzia A LISTA DE EXERCÍCIOS ) Usando a dfinição, vrifiqu s as funçõs a sguir são drivávis m 0 m
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA LIMITES E DERIVADAS MAT B - 008. Prof a Graça Luzia A LISTA DE EXERCÍCIOS ) Usando a dfinição, vrifiqu s as funçõs a sguir são drivávis m 0 m
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA MAT 195 CÁLCULO DIFERENCIAL E INTEGRAL I Atualizada em A LISTA DE EXERCÍCIOS
 INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA MAT 9 CÁLCULO DIFERENCIAL E INTEGRAL I Atualizada m 00. A LISTA DE EXERCÍCIOS Drivadas d Funçõs Compostas 0. Para cada uma das funçõs sguints,
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA MAT 9 CÁLCULO DIFERENCIAL E INTEGRAL I Atualizada m 00. A LISTA DE EXERCÍCIOS Drivadas d Funçõs Compostas 0. Para cada uma das funçõs sguints,
1. (2,0) Um cilindro circular reto é inscrito em uma esfera de raio r. Encontre a maior área de superfície possível para esse cilindro.
 Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
3. Geometria Analítica Plana
 MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DE PELOTAS DEPARTAMENTO DE MATEMÁTICA E ESTATÍSITICA APOSTILA DE GEOMETRIA ANALÍTICA PLANA PROF VINICIUS 3 Gomtria Analítica Plana 31 Vtors no plano Intuitivamnt,
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DE PELOTAS DEPARTAMENTO DE MATEMÁTICA E ESTATÍSITICA APOSTILA DE GEOMETRIA ANALÍTICA PLANA PROF VINICIUS 3 Gomtria Analítica Plana 31 Vtors no plano Intuitivamnt,
Cálculo IV EP7 Tutor
 Fundação ntro d iências Educação Suprior a Distância do Estado do Rio d Janiro ntro d Educação Suprior a Distância do Estado do Rio d Janiro álculo IV EP7 Tutor Ercício 1: Us a intgral d linha para ncontrar
Fundação ntro d iências Educação Suprior a Distância do Estado do Rio d Janiro ntro d Educação Suprior a Distância do Estado do Rio d Janiro álculo IV EP7 Tutor Ercício 1: Us a intgral d linha para ncontrar
LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA
 Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
CONTINUIDADE A idéia de uma Função Contínua
 CONTINUIDADE A idéia d uma Função Contínua Grosso modo, uma função contínua é uma função qu não aprsnta intrrupção ou sja, uma função qu tm um gráfico qu pod sr dsnhado sm tirar o lápis do papl. Assim,
CONTINUIDADE A idéia d uma Função Contínua Grosso modo, uma função contínua é uma função qu não aprsnta intrrupção ou sja, uma função qu tm um gráfico qu pod sr dsnhado sm tirar o lápis do papl. Assim,
66 (5,99%) 103 (9,35%) Análise Combinatória 35 (3,18%)
 Distribuição das 0 Qustõs do I T A 9 (8,6%) 66 (,99%) Equaçõs Irracionais 09 (0,8%) Equaçõs Exponnciais (,09%) Conjuntos 9 (,6%) Binômio d Nwton (,9%) 0 (9,%) Anális Combinatória (,8%) Go. Analítica Funçõs
Distribuição das 0 Qustõs do I T A 9 (8,6%) 66 (,99%) Equaçõs Irracionais 09 (0,8%) Equaçõs Exponnciais (,09%) Conjuntos 9 (,6%) Binômio d Nwton (,9%) 0 (9,%) Anális Combinatória (,8%) Go. Analítica Funçõs
Cálculo Cálculo D Cálculo D Cálculo D D Cálculo Cálculo D
 álculo álculo álculo D D álculo álculo D álculo D Márcia osals ibiro Simch Grmán Márcia amón osals anahualpa ibirosuazo Simch Grmán Silvia amón Pritsch anahualpa Wndt Pinto Suazo Silvia Pritsch Wndt Pinto
álculo álculo álculo D D álculo álculo D álculo D Márcia osals ibiro Simch Grmán Márcia amón osals anahualpa ibirosuazo Simch Grmán Silvia amón Pritsch anahualpa Wndt Pinto Suazo Silvia Pritsch Wndt Pinto
03/04/2014. Força central. 3 O problema das forças centrais TÓPICOS FUNDAMENTAIS DE FÍSICA. Redução a problema de um corpo. A importância do problema
 Força cntral 3 O problma das forças cntrais TÓPICOS FUNDAMENTAIS DE FÍSICA Uma força cntralé uma força (atrativa ou rpulsiva) cuja magnitud dpnd somnt da distância rdo objto à origm é dirigida ao longo
Força cntral 3 O problma das forças cntrais TÓPICOS FUNDAMENTAIS DE FÍSICA Uma força cntralé uma força (atrativa ou rpulsiva) cuja magnitud dpnd somnt da distância rdo objto à origm é dirigida ao longo
EQUAÇÕES DIFERENCIAIS LINEARES DE 2ª ORDEM
 Caítulo II EQUAÇÕES DIFERENCIAIS LINEARES DE ª ORDEM Caítulo II Equaçõs Difrnciais Linars d ª Ordm Caítulo II Até agora já conhcmos uma séri d quaçõs difrnciais linars d rimira ordm Dfinirmos considrarmos
Caítulo II EQUAÇÕES DIFERENCIAIS LINEARES DE ª ORDEM Caítulo II Equaçõs Difrnciais Linars d ª Ordm Caítulo II Até agora já conhcmos uma séri d quaçõs difrnciais linars d rimira ordm Dfinirmos considrarmos
Hewlett-Packard MATRIZES. Aulas 01 a 06. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MATRIZES Aulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MATRIZES NOÇÃO DE MATRIZ REPRESENTAÇÃO DE UMA MATRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDAMENTAL MATRIZES ESPECIAIS IGUALDADE
Hwltt-Packard MATRIZES Aulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MATRIZES NOÇÃO DE MATRIZ REPRESENTAÇÃO DE UMA MATRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDAMENTAL MATRIZES ESPECIAIS IGUALDADE
4.1 Método das Aproximações Sucessivas ou Método de Iteração Linear (MIL)
 4. Método das Aproimaçõs Sucssivas ou Método d Itração Linar MIL O método da itração linar é um procsso itrativo qu aprsnta vantagns dsvantagns m rlação ao método da bisscção. Sja uma função f contínua
4. Método das Aproimaçõs Sucssivas ou Método d Itração Linar MIL O método da itração linar é um procsso itrativo qu aprsnta vantagns dsvantagns m rlação ao método da bisscção. Sja uma função f contínua
Prova Escrita de Matemática A 12. o Ano de Escolaridade Prova 635/Versões 1 e 2
 Eam Nacional d 0 (. a fas) Prova Escrita d Matmática. o no d Escolaridad Prova 3/Vrsõs GRUPO I Itns Vrsão Vrsão. (C) (). () (C) 3. () (C). (D) (). (C) (). () () 7. () (D) 8. (C) (D) Justificaçõs:. P( )
Eam Nacional d 0 (. a fas) Prova Escrita d Matmática. o no d Escolaridad Prova 3/Vrsõs GRUPO I Itns Vrsão Vrsão. (C) (). () (C) 3. () (C). (D) (). (C) (). () () 7. () (D) 8. (C) (D) Justificaçõs:. P( )
Matemática IME-2007/ a QUESTÃO. 2 a QUESTÃO COMENTA
 Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
EQUAÇÕES DIFERENCIAIS
 EQUAÇÕES DIFERENCIAIS Notas d aula Profssor: Altmir José Borgs Curitiba Agosto d 006 EQUAÇÕES DIFERENCIAIS Dfinição: Chama-s quação difrncial à quação qu possui as drivadas ou difrnciais d uma ou mais
EQUAÇÕES DIFERENCIAIS Notas d aula Profssor: Altmir José Borgs Curitiba Agosto d 006 EQUAÇÕES DIFERENCIAIS Dfinição: Chama-s quação difrncial à quação qu possui as drivadas ou difrnciais d uma ou mais
AUTO CENTRAGEM DA PLACA DE RETENÇÃO DE UMA MÁQUINA DE PISTÕES AXIAIS TIPO SWASHPLATE. azevedoglauco@unifei.edu.br
 AUTO CENTRAGEM DA PLACA DE RETENÇÃO DE UMA MÁQUINA DE PISTÕES AXIAIS TIPO SWASHPLATE Glauco José Rodrigus d Azvdo 1, João Zangrandi Filho 1 Univrsidad Fdral d Itajubá/Mcânica, Av. BPS, 1303 Itajubá-MG,
AUTO CENTRAGEM DA PLACA DE RETENÇÃO DE UMA MÁQUINA DE PISTÕES AXIAIS TIPO SWASHPLATE Glauco José Rodrigus d Azvdo 1, João Zangrandi Filho 1 Univrsidad Fdral d Itajubá/Mcânica, Av. BPS, 1303 Itajubá-MG,
Programa de Pós-Graduação Processo de Seleção 2 0 Semestre 2008 Exame de Conhecimento em Física
 UNIVERSIDADE FEDERAL DE GOIAS INSTITUTO DE FÍSICA C.P. 131, CEP 74001-970, Goiânia - Goiás - Brazil. Fon/Fax: +55 62 521-1029 Programa d Pós-Graduação Procsso d Slção 2 0 Smstr 2008 Exam d Conhcimnto m
UNIVERSIDADE FEDERAL DE GOIAS INSTITUTO DE FÍSICA C.P. 131, CEP 74001-970, Goiânia - Goiás - Brazil. Fon/Fax: +55 62 521-1029 Programa d Pós-Graduação Procsso d Slção 2 0 Smstr 2008 Exam d Conhcimnto m
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES
 PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
Memorize as integrais imediatas e veja como usar a técnica de substituição.
 Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
Curso de Engenharia Mecânica Disciplina: Física 2 Nota: Rubrica. Coordenador Professor: Rudson R Alves Aluno:
 Curso d Engnharia Mcânica Disciplina: Física 2 Nota: Rubrica Coordnador Profssor: Rudson R Alvs Aluno: Turma: EA3N Smstr: 1 sm/2017 Data: 20/04/2017 Avaliação: 1 a Prova Valor: 10,0 p tos INSTRUÇÕES DA
Curso d Engnharia Mcânica Disciplina: Física 2 Nota: Rubrica Coordnador Profssor: Rudson R Alvs Aluno: Turma: EA3N Smstr: 1 sm/2017 Data: 20/04/2017 Avaliação: 1 a Prova Valor: 10,0 p tos INSTRUÇÕES DA
FUNÇÕES DE UMA VARIÁVEL COMPLEXA
 FUNÇÕES DE UMA VARIÁVEL COMPLEXA Ettor A. d Barros 1. INTRODUÇÃO Sja s um númro complxo qualqur prtncnt a um conjunto S d númros complxos. Dizmos qu s é uma variávl complxa. S, para cada valor d s, o valor
FUNÇÕES DE UMA VARIÁVEL COMPLEXA Ettor A. d Barros 1. INTRODUÇÃO Sja s um númro complxo qualqur prtncnt a um conjunto S d númros complxos. Dizmos qu s é uma variávl complxa. S, para cada valor d s, o valor
PROGRAMA DE REESTRUTURAÇÃO DA UNIDADE
 Campus d Ilha Soltira PROGRAMA DE REESTRUTURAÇÃO DA UNIDADE Aos dz (10) dias do mês d stmbro (09) do ano d dois mil doz (2012), na Sala d Runiõs da Congrgação, as parts abaio nomadas tomaram ciência do
Campus d Ilha Soltira PROGRAMA DE REESTRUTURAÇÃO DA UNIDADE Aos dz (10) dias do mês d stmbro (09) do ano d dois mil doz (2012), na Sala d Runiõs da Congrgação, as parts abaio nomadas tomaram ciência do
Exercício 2. Calcule. f (x)<0 e f (x) e M 2 = f (0.5) =1.3 Logo
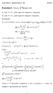 Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
Dinâmica Longitudinal do Veículo
 Dinâmica Longitudinal do Vículo 1. Introdução A dinâmica longitudinal do vículo aborda a aclração frnagm do vículo, movndo-s m linha rta. Srão aqui usados os sistmas d coordnadas indicados na figura 1.
Dinâmica Longitudinal do Vículo 1. Introdução A dinâmica longitudinal do vículo aborda a aclração frnagm do vículo, movndo-s m linha rta. Srão aqui usados os sistmas d coordnadas indicados na figura 1.
INSTITUTO POLITÉCNICO DE VISEU. f x = x em relação à partição do intervalo. em 4 subintervalos de igual amplitude e tal que o ponto ω
 INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA Dparamno Mamáica Disciplina Anális Mamáica Curso Engnharia Informáica º Smsr º Ficha nº : Cálculo ingral m IR Drmin a soma d Rimann da função
INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA Dparamno Mamáica Disciplina Anális Mamáica Curso Engnharia Informáica º Smsr º Ficha nº : Cálculo ingral m IR Drmin a soma d Rimann da função
Hewlett-Packard MATRIZES. Aulas 01 a 05. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MTRIZES ulas 0 a 05 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE ENTRE
Hwltt-Packard MTRIZES ulas 0 a 05 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE ENTRE
TEMA 3 NÚMEROS COMPLEXOS FICHAS DE TRABALHO 12.º ANO COMPILAÇÃO TEMA 3 NÚMEROS COMPLEXOS. Jorge Penalva José Carlos Pereira Vítor Pereira MathSuccess
 FICHAS DE TRABALHO º ANO COMPILAÇÃO TEMA NÚMEROS COMPLEXOS Sit: http://wwwmathsuccsspt Facbook: https://wwwfacbookcom/mathsuccss TEMA NÚMEROS COMPLEXOS Matmática A º Ano Fichas d Trabalho Compilação Tma
FICHAS DE TRABALHO º ANO COMPILAÇÃO TEMA NÚMEROS COMPLEXOS Sit: http://wwwmathsuccsspt Facbook: https://wwwfacbookcom/mathsuccss TEMA NÚMEROS COMPLEXOS Matmática A º Ano Fichas d Trabalho Compilação Tma
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ - UTFPR CAMPUS CORNÉLIO PROCÓPIO
 MINISÉRIO DA EDUCAÇÃO UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ - UFPR CAMPUS CORNÉLIO PROCÓPIO PR UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ Noçõs básicas d unçõs d várias variávis FUNÇÕES DE VARIAS VARIÁVEIS
MINISÉRIO DA EDUCAÇÃO UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ - UFPR CAMPUS CORNÉLIO PROCÓPIO PR UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ Noçõs básicas d unçõs d várias variávis FUNÇÕES DE VARIAS VARIÁVEIS
SISTEMA DE PONTO FLUTUANTE
 Lógica Matmática Computacional - Sistma d Ponto Flutuant SISTEM DE PONTO FLUTUNTE s máquinas utilizam a sguint normalização para rprsntação dos númros: 1d dn * B ± 0d L ond 0 di (B 1), para i = 1,,, n,
Lógica Matmática Computacional - Sistma d Ponto Flutuant SISTEM DE PONTO FLUTUNTE s máquinas utilizam a sguint normalização para rprsntação dos númros: 1d dn * B ± 0d L ond 0 di (B 1), para i = 1,,, n,
Hewlett-Packard MATRIZES. Aulas 01 a 06. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MTRIZES ulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz no 06 Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE
Hwltt-Packard MTRIZES ulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz no 06 Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE
Augusto Massashi Horiguti. Doutor em Ciências pelo IFUSP Professor do CEFET-SP. Palavras-chave: Período; pêndulo simples; ângulos pequenos.
 DETERMNAÇÃO DA EQUAÇÃO GERAL DO PERÍODO DO PÊNDULO SMPLES Doutor m Ciências plo FUSP Profssor do CEFET-SP Est trabalho aprsnta uma rvisão do problma do pêndulo simpls com a dmonstração da quação do príodo
DETERMNAÇÃO DA EQUAÇÃO GERAL DO PERÍODO DO PÊNDULO SMPLES Doutor m Ciências plo FUSP Profssor do CEFET-SP Est trabalho aprsnta uma rvisão do problma do pêndulo simpls com a dmonstração da quação do príodo
UFJF ICE Departamento de Matemática Cálculo I Terceira Avaliação 10/07/2010 FILA A Aluno (a): Matrícula: Turma:
 UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação 0/07/00 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha.
UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação 0/07/00 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha.
Questões para o concurso de professores Colégio Pedro II
 Qustõs para o concurso d profssors Colégio Pdro II Profs Marilis, Andrzinho Fábio Prova Discursiva 1ª QUESTÃO Jhosy viaja com sua sposa, Paty, sua filha filho para a Rgião dos Lagos para curtir um friadão
Qustõs para o concurso d profssors Colégio Pdro II Profs Marilis, Andrzinho Fábio Prova Discursiva 1ª QUESTÃO Jhosy viaja com sua sposa, Paty, sua filha filho para a Rgião dos Lagos para curtir um friadão
EXAME NACIONAL DO ENSINO SECUNDÁRIO VERSÃO 1
 EXAME NACIONAL DO ENSINO SECUNDÁRIO 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) Cursos Gerais e Cursos Tecnológicos PROVA 435/9 Págs. Duração da prova: 120 minutos 2005 1.ª FASE
EXAME NACIONAL DO ENSINO SECUNDÁRIO 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) Cursos Gerais e Cursos Tecnológicos PROVA 435/9 Págs. Duração da prova: 120 minutos 2005 1.ª FASE
Geometria Analítica - Aula
 Gomtria Analítica - Aula 0 60 K. Frnsl - J. Dlgado Aula 1 1. Rotação dos ixos coordnados Sja OXY um sistma d ixos ortogonais no plano sja O X Y o sistma d ixos obtido girando os ixos OX OY d um ângulo
Gomtria Analítica - Aula 0 60 K. Frnsl - J. Dlgado Aula 1 1. Rotação dos ixos coordnados Sja OXY um sistma d ixos ortogonais no plano sja O X Y o sistma d ixos obtido girando os ixos OX OY d um ângulo
CAPÍTULO 06 ESTUDOS DE FILAS EM INTERSEÇÕES NÃO SEMAFORIZADAS
 APÍTULO 06 ESTUDOS DE FILAS EM INTERSEÇÕES NÃO SEMAFORIZADAS As filas m intrsçõs não smaforizadas ocorrm dvido aos movimntos não prioritários. O tmpo ncssário para ralização da manobra dpnd d inúmros fators,
APÍTULO 06 ESTUDOS DE FILAS EM INTERSEÇÕES NÃO SEMAFORIZADAS As filas m intrsçõs não smaforizadas ocorrm dvido aos movimntos não prioritários. O tmpo ncssário para ralização da manobra dpnd d inúmros fators,
CAPÍTULO 9 COORDENADAS POLARES
 Luiz Frncisco d Cruz Drtmnto d Mtmátic Uns/Buru CAPÍTULO 9 COORDENADAS POLARES O lno, tmbém chmdo d R, ond R RR {(,)/, R}, ou sj, o roduto crtsino d R or R, é o conjunto d todos os rs ordndos (,), R El
Luiz Frncisco d Cruz Drtmnto d Mtmátic Uns/Buru CAPÍTULO 9 COORDENADAS POLARES O lno, tmbém chmdo d R, ond R RR {(,)/, R}, ou sj, o roduto crtsino d R or R, é o conjunto d todos os rs ordndos (,), R El
TÓPICOS. ordem; grau; curvas integrais; condições iniciais e fronteira. 1. Equações Diferenciais. Conceitos Gerais.
 Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
CPV O Cursinho que Mais Aprova na GV
 PV O ursinho que Mais Aprova na GV FGV ADM 1/dez/01 MATEMÁTIA APLIADA 01. Um mapa de um pequeno parque é uma região em forma de quadrilátero, limitado pelas retas y = x, y = x +, y = x + e y = x, sendo
PV O ursinho que Mais Aprova na GV FGV ADM 1/dez/01 MATEMÁTIA APLIADA 01. Um mapa de um pequeno parque é uma região em forma de quadrilátero, limitado pelas retas y = x, y = x +, y = x + e y = x, sendo
Universidade Federal de Viçosa
 Universidade Federal de Viçosa Ciências Eatas e Tecnológicas Departamento de Matemática MAT 4 - Lista - 07/. Determine o domínio a imagem as raízes e o estudo de sinal das funções a seguir: (a) f() = 4
Universidade Federal de Viçosa Ciências Eatas e Tecnológicas Departamento de Matemática MAT 4 - Lista - 07/. Determine o domínio a imagem as raízes e o estudo de sinal das funções a seguir: (a) f() = 4
Lista 9: Integrais: Indefinidas e Definidas e Suas Aplicações
 GOVERNO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO CÂMPUS JUAZEIRO/BA COLEG. DE ENG. ELÉTRICA PROF. PEDRO MACÁRIO DE MOURA MATEMÁTICA APLICADA À ADM 5. Lista 9: Intgrais:
GOVERNO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO CÂMPUS JUAZEIRO/BA COLEG. DE ENG. ELÉTRICA PROF. PEDRO MACÁRIO DE MOURA MATEMÁTICA APLICADA À ADM 5. Lista 9: Intgrais:
UCP Gestão/Economia Matemática II 9 de Abril de 2010
 UCP Gstão/Economia Matmática II 9 d Abril d 00 ª frquência h30m GRUPO (.5). Sja f ( x, ) x com x u uv, u sn t, v log( t ). Calcul df dt. z4 x (.0). Dtrmin a drivada da função f x no ponto P (,,) na dircção
UCP Gstão/Economia Matmática II 9 d Abril d 00 ª frquência h30m GRUPO (.5). Sja f ( x, ) x com x u uv, u sn t, v log( t ). Calcul df dt. z4 x (.0). Dtrmin a drivada da função f x no ponto P (,,) na dircção
Justifique todas as passagens
 ā Prova d Cálculo II - MAT2 - IOUSP /2/204 Nom : GABARITO N ō USP : Profssor : Oswaldo Rio Branco d Olivira Justifiqu todas as passagns Q 2 4 5 Total N. Considr a função f : R 2 R dfinida por f(x,y) =
ā Prova d Cálculo II - MAT2 - IOUSP /2/204 Nom : GABARITO N ō USP : Profssor : Oswaldo Rio Branco d Olivira Justifiqu todas as passagns Q 2 4 5 Total N. Considr a função f : R 2 R dfinida por f(x,y) =
TÓPICOS. EDO de variáveis separadas. EDO de variáveis separáveis. EDO homogénea. 2. Equações Diferenciais de 1ª Ordem.
 ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
PROCESSO SELETIVO DO PRIMEIRO SEMESTRE DE 2015 PROVA DE PROCESSOS DE TRANSFORMAÇÃO METAL-MECÂNICA
 PROVA DE PROCESSOS DE TRANSFORMAÇÃO METAL-MECÂNICA Um metal deforma-se plasticamente segundo a curva Y = 400 + 700 e 0,4. Deseja-se trefilar um fio circular deste metal do diâmetro inicial 8 mm, promovendo
PROVA DE PROCESSOS DE TRANSFORMAÇÃO METAL-MECÂNICA Um metal deforma-se plasticamente segundo a curva Y = 400 + 700 e 0,4. Deseja-se trefilar um fio circular deste metal do diâmetro inicial 8 mm, promovendo
Vestibular Comentado - UVA/2011.1
 Vestibular Comentado - UV/0. MTEMÁTIC Comentários: Profs. Dewayne, Eliano Bezerra, Marcos urélio 9. Considere o polinômio p(x)=ax + bx + c com a 0. Sejam, suas raízes reais distintas. Sobre as raízes do
Vestibular Comentado - UV/0. MTEMÁTIC Comentários: Profs. Dewayne, Eliano Bezerra, Marcos urélio 9. Considere o polinômio p(x)=ax + bx + c com a 0. Sejam, suas raízes reais distintas. Sobre as raízes do
MATEMÁTICA A - 12o Ano N o s Complexos - Equações e problemas
 MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Exercícios de exames e testes intermédios 1. Em C, conjunto dos números complexos, considere z = + i19 cis θ Determine os valores de θ pertencentes
MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Exercícios de exames e testes intermédios 1. Em C, conjunto dos números complexos, considere z = + i19 cis θ Determine os valores de θ pertencentes
MATEMÁTICA I ECONOMIA (5598) Ficha de exercícios 1 (2012/2013)
 Universidade da Beira Interior - Departamento de Matemática MATEMÁTICA I ECONOMIA (5598) Ficha de eercícios (0/03). Determine o conjunto dos pontos interiores, eteriores e fronteiros dos seguintes conjuntos:
Universidade da Beira Interior - Departamento de Matemática MATEMÁTICA I ECONOMIA (5598) Ficha de eercícios (0/03). Determine o conjunto dos pontos interiores, eteriores e fronteiros dos seguintes conjuntos:
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Matemática Aplicada. Qual é a altitude do centro do parque, ponto de encontro das diagonais, em relação ao nível do mar?
 Matemática Aplicada 1 Um mapa de um pequeno parque é uma região em forma de quadrilátero, limitado pelas retas y = x, y = x +, y = x + e y = x, sendo que as unidades estão em quilômetros. A altitude em
Matemática Aplicada 1 Um mapa de um pequeno parque é uma região em forma de quadrilátero, limitado pelas retas y = x, y = x +, y = x + e y = x, sendo que as unidades estão em quilômetros. A altitude em
Capítulo 6 - Integral Inde nida
 Caítulo - Integral Inde nida. Calcule as integrais inde nidas abaio usando integração imediata ou o método da substituição. e d (j) e d d e ( ) (k) d d arctan (l) ( ) d d sec tg (m) d ln d e (n) ( e )
Caítulo - Integral Inde nida. Calcule as integrais inde nidas abaio usando integração imediata ou o método da substituição. e d (j) e d d e ( ) (k) d d arctan (l) ( ) d d sec tg (m) d ln d e (n) ( e )
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
a) (0.2 v) Justifique que a sucessão é uma progressão aritmética e indique o valor da razão.
 MatPrp / Matmática Prparatória () unidad tra curricular / E-Fólio B 8 dzmbro a janiro Critérios d corrção orintaçõs d rsposta Qustão ( val) Considr a sucssão d númros rais dfinida por a) ( v) Justifiqu
MatPrp / Matmática Prparatória () unidad tra curricular / E-Fólio B 8 dzmbro a janiro Critérios d corrção orintaçõs d rsposta Qustão ( val) Considr a sucssão d númros rais dfinida por a) ( v) Justifiqu
Experiência n 2 1. Levantamento da Curva Característica da Bomba Centrífuga Radial HERO
 8 Expriência n 1 Lvantamnto da Curva Caractrística da Bomba Cntrífuga Radial HERO 1. Objtivo: A prsnt xpriência tm por objtivo a familiarização do aluno com o lvantamnto d uma CCB (Curva Caractrística
8 Expriência n 1 Lvantamnto da Curva Caractrística da Bomba Cntrífuga Radial HERO 1. Objtivo: A prsnt xpriência tm por objtivo a familiarização do aluno com o lvantamnto d uma CCB (Curva Caractrística
EQUAÇÕES DIFERENCIAIS NOTAS DE AULA
 Ministério da Educação Univrsidad Tcnológica Fdral do Paraná ampus uritiba Grência d Ensino Psquisa Dpartamnto Acadêmico d Matmática EQUAÇÕES DIFERENIAIS NOTAS DE AULA Equaçõs Difrnciais AULA 0 EQUAÇÕES
Ministério da Educação Univrsidad Tcnológica Fdral do Paraná ampus uritiba Grência d Ensino Psquisa Dpartamnto Acadêmico d Matmática EQUAÇÕES DIFERENIAIS NOTAS DE AULA Equaçõs Difrnciais AULA 0 EQUAÇÕES
Quadro de Respostas das Questões de Múltipla Escolha Valor: 65 pontos Alternativa/Questão Rascunho A B C D E. 1 e.
 UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação /08/0 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação /08/0 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
PSI-2432: Projeto e Implementação de Filtros Digitais Projeto Proposto: Conversor de taxas de amostragem
 PSI-2432: Projto Implmntação d Filtros Digitais Projto Proposto: Convrsor d taxas d amostragm Migul Arjona Ramírz 3 d novmbro d 2005 Est projto consist m implmntar no MATLAB um sistma para troca d taxa
PSI-2432: Projto Implmntação d Filtros Digitais Projto Proposto: Convrsor d taxas d amostragm Migul Arjona Ramírz 3 d novmbro d 2005 Est projto consist m implmntar no MATLAB um sistma para troca d taxa
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
7.1 Mudança de Variável (método de substituição)
 7. Mudança de Variável (método de substituição) 0. 0. 0. 05. 07. 08. 0... e 5 (res. e 5 =5 + C) sen a (res. a cos a + C; a 6= 0) sen () 7 (res. cotg + C) (res. jln 7j + C) tan (res. ln jcos j + C) cot
7. Mudança de Variável (método de substituição) 0. 0. 0. 05. 07. 08. 0... e 5 (res. e 5 =5 + C) sen a (res. a cos a + C; a 6= 0) sen () 7 (res. cotg + C) (res. jln 7j + C) tan (res. ln jcos j + C) cot
Universidade Federal do Rio de Janeiro INSTITUTO DE MATEMÁTICA Departamento de Matemática
 Univrsidad Fdral do Rio d Janiro INSTITUTO DE MATEMÁTICA Dpartamnto d Matmática Gabarito da 1 a prova d Gomtria difrncial - 20/09/2018 - Mônica 1. Sja α(s) uma curva rgular plana paramtrizada plo comprimnto
Univrsidad Fdral do Rio d Janiro INSTITUTO DE MATEMÁTICA Dpartamnto d Matmática Gabarito da 1 a prova d Gomtria difrncial - 20/09/2018 - Mônica 1. Sja α(s) uma curva rgular plana paramtrizada plo comprimnto
Álgebra. Matrizes. . Dê o. 14) Dada a matriz: A =.
 Matrizs ) Dada a matriz A = Dê o su tipo os lmntos a, a a ) Escrva a matriz A, do tipo x, ond a ij = i + j ) Escrva a matriz A x, ond a ij = i +j ) Escrva a matriz A = (a ij ) x, ond a ij = i + j ) Escrva
Matrizs ) Dada a matriz A = Dê o su tipo os lmntos a, a a ) Escrva a matriz A, do tipo x, ond a ij = i + j ) Escrva a matriz A x, ond a ij = i +j ) Escrva a matriz A = (a ij ) x, ond a ij = i + j ) Escrva
INSTITUTO SUPERIOR DE ECONOMIA E GESTÃO Estatística I - Licenciatura em MAEG 2º Ano PADEF Junho 2005 Parte teórica Prova Nome: Nº
 Estatística I - Licnciatura m MAEG º Ano PADEF Junho 5 Part tórica Prova 753519 Nom: Nº 1. Prguntas d rsposta fchada ( valors) Para cada afirmação, assinal s sta é Vrdadira (V) ou Falsa (F). Uma rsposta
Estatística I - Licnciatura m MAEG º Ano PADEF Junho 5 Part tórica Prova 753519 Nom: Nº 1. Prguntas d rsposta fchada ( valors) Para cada afirmação, assinal s sta é Vrdadira (V) ou Falsa (F). Uma rsposta
1) Determine o domínio das funções abaixo e represente-o graficamente: 1 1
 ) Dtrmin dmíni das funçõs abai rprsnt- graficamnt: z + z 4.ln( ) z ln z z arccs( ) f) z g) z ln + h) z ( ) ) Dtrmin dmíni, trac as curvas d nívl sbc gráfic das funçõs: f (, ) 9 + 4 f (, ) 6 f (, ) 6 f
) Dtrmin dmíni das funçõs abai rprsnt- graficamnt: z + z 4.ln( ) z ln z z arccs( ) f) z g) z ln + h) z ( ) ) Dtrmin dmíni, trac as curvas d nívl sbc gráfic das funçõs: f (, ) 9 + 4 f (, ) 6 f (, ) 6 f
Departamento de Engenharia Elétrica CONTROLE DIGITAL
 Dpartamnto d Engnharia Elétrica CONTROLE DIGITAL PROF. DR. EDVALDO ASSUNÇÃO Univrsidad Estadual Paulista UNESP Faculdad d Engnharia d Ilha Soltira FEIS Dpartamnto d Engnharia Elétrica DEE -03- Sumário
Dpartamnto d Engnharia Elétrica CONTROLE DIGITAL PROF. DR. EDVALDO ASSUNÇÃO Univrsidad Estadual Paulista UNESP Faculdad d Engnharia d Ilha Soltira FEIS Dpartamnto d Engnharia Elétrica DEE -03- Sumário
PROVA DE MATEMÁTICA PARA OS CANDIDATOS MAIORES DE 23 ANOS
 PROVA DE MATEMÁTICA PARA OS CANDIDATOS MAIORES DE ANOS Duração: 60 minutos Nome: 1ª Parte Para cada uma das seguintes questões de escolha múltipla, seleccione a resposta correcta com um círculo de entre
PROVA DE MATEMÁTICA PARA OS CANDIDATOS MAIORES DE ANOS Duração: 60 minutos Nome: 1ª Parte Para cada uma das seguintes questões de escolha múltipla, seleccione a resposta correcta com um círculo de entre
Módulo de Círculo Trigonométrico. Secante, Cossecante e Cotangente. 1 a série E.M.
 Módulo d Círculo Trigonométrico Scant, Cosscant Cotangnt a séri EM Círculo Trigonométrico Scant, Cosscant Cotangnt Exrcícios Introdutórios ] π Exrcício Sja α ; π tal qu sn α, dtrmin, s xistir, o rsultado
Módulo d Círculo Trigonométrico Scant, Cosscant Cotangnt a séri EM Círculo Trigonométrico Scant, Cosscant Cotangnt Exrcícios Introdutórios ] π Exrcício Sja α ; π tal qu sn α, dtrmin, s xistir, o rsultado
 Se padieira 135mm = 110mm COLOCAR A CURVA: -Se ombreira do lado da curva (C) é menor que 440mm: usar a cota 290mm -Se a ombreira (C) é maior que 440mm usar a cota de 45mm
Se padieira 135mm = 110mm COLOCAR A CURVA: -Se ombreira do lado da curva (C) é menor que 440mm: usar a cota 290mm -Se a ombreira (C) é maior que 440mm usar a cota de 45mm
FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS DE SERGIPE ASSUNTO: DERIVADAS E INTEGRAIS DAS FUNÇÕES, TRIGONOMÉTRICAS E HIPÉRBOLICAS INVERSAS
 FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS DE SERGIPE CURSO: ENGENHARIA DE PRODUÇÃO ASSUNTO: DERIVADAS E INTEGRAIS DAS FUNÇÕES, TRIGONOMÉTRICAS E HIPÉRBOLICAS INVERSAS PROFESSOR: MARCOS AGUIAR CÁLCULO I. FUNÇÕES
FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS DE SERGIPE CURSO: ENGENHARIA DE PRODUÇÃO ASSUNTO: DERIVADAS E INTEGRAIS DAS FUNÇÕES, TRIGONOMÉTRICAS E HIPÉRBOLICAS INVERSAS PROFESSOR: MARCOS AGUIAR CÁLCULO I. FUNÇÕES
Coordenadas Polares. Prof. Márcio Nascimento. marcio@matematicauva.org
 Coordenadas Polares Prof. Márcio Nascimento marcio@matematicauva.org Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática
Coordenadas Polares Prof. Márcio Nascimento marcio@matematicauva.org Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Hewlett-Packard CONJUNTOS NUMÉRICOS. Aulas 01 a 06. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos
 Hwltt-Packard CONJUNTOS NUMÉRICOS Aulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz Ramos Ano: 206 Sumário CONJUNTOS NUMÉRICOS 2 Conjunto dos númros Naturais 2 Conjunto dos númros Intiros 2 Conjunto
Hwltt-Packard CONJUNTOS NUMÉRICOS Aulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz Ramos Ano: 206 Sumário CONJUNTOS NUMÉRICOS 2 Conjunto dos númros Naturais 2 Conjunto dos númros Intiros 2 Conjunto
Adriano Pedreira Cattai
 Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
TÓPICOS DE MATEMÁTICA PROF.: PATRÍCIA ALVES
 TÓPICOS DE MATEMÁTICA PROF.: PATRÍCIA ALVES 33 MATRIZES 1. Dê o tipo d cada uma das sguints prtncm às diagonais principais matrizs: scundárias d A. 1 3 a) A 7 2 7. Qual é o lmnto a 46 da matriz i j 2 j
TÓPICOS DE MATEMÁTICA PROF.: PATRÍCIA ALVES 33 MATRIZES 1. Dê o tipo d cada uma das sguints prtncm às diagonais principais matrizs: scundárias d A. 1 3 a) A 7 2 7. Qual é o lmnto a 46 da matriz i j 2 j
FÍSICA 3. k = 1/4πε 0 = 9,0 10 9 N.m 2 /c 2 1 atm = 1,0 x 10 5 N/m 2 tan 17 = 0,30. a (m/s 2 ) 30 20 10 1,0 2,0 3,0 4,0 5,0.
 FÍSIC 3 Valores de algumas grandezas físicas celeração da gravidade: 1 m/s Carga do elétron: 1,6 x 1-19 C Constante de Planck: 6,6 x 1-34 J Velocidade da luz: 3 x 1 8 m/s k = 1/4πε = 9, 1 9 N.m /c 1 atm
FÍSIC 3 Valores de algumas grandezas físicas celeração da gravidade: 1 m/s Carga do elétron: 1,6 x 1-19 C Constante de Planck: 6,6 x 1-34 J Velocidade da luz: 3 x 1 8 m/s k = 1/4πε = 9, 1 9 N.m /c 1 atm
Aula Expressão do produto misto em coordenadas
 Aula 15 Nsta aula vamos xprssar o produto misto m trmos d coordnadas, analisar as propridads dcorrnts dssa xprssão fazr algumas aplicaçõs intrssants dos produtos vtorial misto. 1. Exprssão do produto misto
Aula 15 Nsta aula vamos xprssar o produto misto m trmos d coordnadas, analisar as propridads dcorrnts dssa xprssão fazr algumas aplicaçõs intrssants dos produtos vtorial misto. 1. Exprssão do produto misto
