PUCRS - FENG - DEE - Mestrado em Engenharia Elétrica Redes Neurais Artificiais Fernando César C. de Castro e Maria Cristina F. de Castro.
|
|
|
- Ayrton Fraga Álvaro
- 8 Há anos
- Visualizações:
Transcrição
1 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Capítulo 6 Redes Neuras Artfcas para Decoposção de u Espaço Vetoral e Sub-Espaços Nos capítulos aterores estudaos detalhadaete dos tpos de RNAs que apreseta a especal habldade de apreder a partr de seu abete e, a partr do processo de apredzado supervsoado, elhorar seu desepeho as RNAs LPs treadas pelo algorto backpropagato e as RNAs RBFs. Neste capítulo estudareos u tpo de RNA que é subetdo a u processo de apredzado ão-supervsoado ou auto-orgazado. O propósto de u algorto de apredzado auto-orgazado é descobrr padrões sgfcatvos ou característcas os dados de etrada da RNA, e fazê-lo se a preseça de u tutor ou sea, se a preseça de u couto de alvos de teresse, provdos por u tutor etero. Para atgr tal propósto, o algorto é provdo de u couto de regras de atureza local, couto este que o hablta a apreder a coputar u apeaeto etradasaída, co específcas propredades deseáves. O tero "local" sgfca, este coteto, que ua udaça aplcada ao peso sáptco de u eurôo é cofada à vzhaça edata daquele eurôo. O odelaeto de estruturas de RNAs usadas para apredzado auto-orgazado tede uto as a segur as estruturas euro-bológcas do que as estruturas utlzadas para o apredzado supervsoado. A heurístca para apredzado auto-orgazado de Redes Neuras Artfcas que estudareos este capítulo é chaada "Algorto Hebbao Geeralzado" e é utlzada para proceder à Aálse dos Copoetes Prcpas Prcpal Copoets Aalyss - 1
2 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro PCA ou Decoposção e Sub-Espaços DSE de u couto da dados de teresse. O Algorto Hebbao Geeralzado fo proposto por Sager e 1989 [4] e coba a ortooralzação de Gra-Schdt [1] ao odelo de u úco eurôo lear troduzdo por Oa e 198 [4]. A Aálse dos Copoetes Prcpas de u couto de dados é ua técca padrão couete utlzada para redução da desoaldade de dados, e processaeto de sas. Para troduzr o assuto, preraete reos descrever os prcípos que rege o apredzado auto-orgazado. Na seqüêca, estudareos a rasforada Karhue- Loève, que costtu o coheceto básco ecessáro ao estudo das RNAs utlzadas para Aálse dos Copoetes Prcpas ou Decoposção e Sub-Espaços, que são o obetvo deste capítulo. 6.1 Prcípos do Apredzado Auto-Orgazado Cofore estudaos o Capítulo, o apredzado ão-supervsoado ou autoorgazado cosste da odfcação repetda dos parâetros lvres de ua RNA e resposta a padrões de atvação e de acordo co regras prescrtas, até que sea desevolvda ua deseada cofguração fal. A razão pela qual a cofguração fal obtda ão é qualquer e, s, ua cofguração útl, resde a segute afratva: Orde global pode surgr a partr de terações locas. Esta afratva é tato válda para o cérebro, quato o coteto de redes euras artfcas. E geral, utas terações locas orgalete aleatóras etre eurôos vzhos de ua rede pode "aalgaar-se" ou, e outra terpretação alegórca, "crstalzar-se" e estados de orde global e coduzr a u coportaeto coerete a fora de padrões espacas ou teporas, o que é a essêca da auto-orgazação.
3 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro A orgazação ocorre e dos dferetes íves, que terage etre s a fora de u elo de realetação. Estes dos íves são:! Atvdade Certos padrões de atvdade são produzdos por ua dada rede e resposta a sas de etrada.! Coectvdade Os pesos sáptcos da rede são odfcados e resposta a sas euras os padrões de atvdade, devdo à plastcdade sáptca. O elo de realetação etre as udaças os pesos sáptcos e as udaças os padrões de atvdade deve ser postvo para que se obteha auto-orgazação da rede. De acordo co este crtéro pode ser etraído o prero prcípo da auto-orgazação, devdo a vo der alsburg 199: 1. odfcações e pesos sáptcos tede a se auto-aplfcar. O processo de auto-aplfcação é restrto pelo requereto de que odfcações e pesos sáptcos deve ser baseadas e sas dspoíves localete, chaados sas pré-sáptcos e pós-sáptcos. Os requeretos de auto-reforço e localdade especfca o ecaso por eo do qual ua forte sapse coduz à cocdêca de sas pré e pós-sáptcos. Por outro lado, a sapse é auetada e força, por tal cocdêca. Este ecaso ada as é do que o postulado de apredzado de Hebb, estudado o Capítulo Processos de Apredzado, que dz: Se dos eurôos e cada lado de ua sapse são atvados sultaeaete, etão a força daquela sapse é seletvaete auetada. Para que o sstea possa ser establzado precsa haver algua fora de copetção por recursos "ltados". Especfcaete, u aueto a força de algua sapse a rede deve ser copesado pelo decrésco e outras. 3
4 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Ass, apeas as sapses que obtê sucesso pode crescer, equato as que obtê eos sucesso tede a efraquecer e pode evetualete desaparecer. Esta observação os leva a abstrar o segudo prcípo da auto-orgazação vo der alsburg, 199:. Ltação de recursos coduz à copetção etre as sapses e, coseqüeteete, à seleção das sapses que cresce de fora as vgorosa portato, as as adequadas às custas de outras. Este prcípo é tabé possível devdo à plastcdade sáptca. Cosdereos agora que ua úca sapse, por cota própra, ão pode produzr de fora efcete evetos favoráves. Para que tal sea possível, é ecesssáro estr cooperação etre u couto de sapses que coverge para u partcular eurôo, levado sas cocdetes, fortes o sufcete para atvar aquele eurôo. Desta observação podeos abstrar o tercero prcípo da auto-orgazação, tabé devdo à vo der alsburg, 199: 3. odfcações e pesos sáptcos tede a cooperar. A preseça de ua sapse vgorosa pode elhorar a adequação de outras sapses, apesar da copetção global a rede. Esta fora de cooperação pode surgr devdo à plastcdade sáptca, ou devdo ao estíulo sultâeo de eurôos pré-sáptcos, decorrete da estêca de codções propícas o abete etero. odos os três prcípos de auto-orgazação até agora descrtos são relacoados soete à própra RNA. Etretato, para que o apredzado auto-orgazado possa desepehar ua fução útl de processaeto de foração, é ecessáro que haa redudâca os padrões de atvação suprdos à rede pelo abete. O quarto prcípo do apredzado auto-orgazado devdo a Barlo, 1989 pode ser, etão, descrto coo segue: 4
5 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro 4. Orde e estrutura os padrões de atvação represeta a foração redudate que é adqurda pela rede eural a fora de coheceto, a qual é pré-requsto ecessáro ao apredzado auto-orgazado. Ua parte deste coheceto pode ser obtda através da observação de parâetros estatístcos, tas co éda, varâca e atrz de correlação dos dados de etrada. Os quatro prcípos do apredzado auto-orgazado costtue a base dos algortos adaptatvos para aálse de copoetes prcpas ou decoposção e subespaços que estudareos este capítulo. Serve tabé para o estudo dos apas autoorgazados de Kohoe Self-Orgazg ap SO que estudareos o capítulo segute deste trabalho. 6. A rasforação Karhue-Lòeve para PCA ou DSE de u Espaço Vetoral A rasforação Karhue-Loève KL proeta u couto X de vetores de dados R sobre ua base ortooral e R forada pelo couto dos auto-vetores e R, =,1,, 1!, da atrz de covarâca de X. A KL é tal que a base será oretada de acordo co as dreções de aor varâca de X e [3][4][5][6][7]. R [1][] A -ésa proeção de X sobre a dreção do auto-vetor e é chaada de -éso sub-espaço ou -éso copoete prcpal. O -éso auto-valor λ assocado ao auto-vetor e correspode à varâca do -éso sub-espaço de X. Ada, a varâca de cada sub-espaço é u áo local, o uverso de todas as varâcas resultates da proeção de X sobre todas as possíves dreções e R. Ebora qualquer espaço de desão eor do que R sea u sub-espaço de R, este estudo refere-se utas vezes a u sub-espaço de X coo o couto dos vetores de X que cocetra-se de 5
6 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro fora alhada ao logo de ua partcular dreção e R. Ada que esta referêca ão sea precsa, ulgou-se váldo aplcá-la devdo ao coceto tutvo ela plícto. alvez a as portate utlzação da rasforação Karhue-Loève, tabé cohecda por Aálse dos Copoetes Prcpas PCA, sea a redução desoal do couto X. Esta característca tora a KL bastate popular e processaeto dgtal de sas por pertr que as forações as sgfcatvas cotdas e u sal possa ser represetadas, edate a trodução de algu erro cosderado acetável, e u espaço de dados de eores desões do que a desão orgal R. Coo cada sub-espaço ou copoete prcpal é oretado de acordo co as dreções de aor varâca de X e R, os sub-espaços de eor varâca pode ser descartados o que resultará e ua redução desoal óta o setdo do Erro édo Quadrátco SE - ea Square Error [3][4][5][6]. O desevolveto do étodo para aplcação da KL à X apresetado este estudo segue a proposta de Hayk e [7]. R Sea X u processo estocástco vetoral represetado pelo couto X de vetores. Caso X ão possua éda zero e, portato, caso o vetor aleatóro ão possua éda zero o vetor éda deverá ser subtraído dos vetores de X ates de car a trasforação,.e., = E{} ode E {} é operador que resulta o valor esperado estatístco éda estatístca do argueto. Sea e R u vetor utáro e adesoal qualquer, sobre o qual será proetado u vetor 6.1. X. Sedo e u vetor utáro, a ora Eucldaa de e é dada pela Equação e 6.1 = e e = 1 Coo e é utáro e adesoal, o taaho ora Eucldaa do vetor que resulta da proeção de sobre e, deoada de proeção a, possu a esa udade desoal de, e é dado pela Equação 6.. 6
7 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro a = e = e 6. Portato, a defe o taaho da proeção do vetor a dreção do vetor e. A proeção a tabé é ua varável aleatóra, co éda e varâca assocadas à estatístca do vetor aleatóro. A éda da proeção a é dada por ode { } A varâca da proeção a é dada por E E { a } E { e } = 6.3 { a } = e E { } = = a 6.4 { } σ a 6.5 a = E { e e } σ E 6.6 σ e E { }e 6.7 a = E é a atrz de covarâca C, de desões, do couto X de vetores R. Nota: Na prátca vetores cohecdos e X. C é aproado por = 1 L 1 L = Retorado à Equação 6.7, coo C = E { } ode observa-se que a varâca Epressado ateatcaete, C sedo L o úero total de, pode-se escrever que σ = e e 6.8 a C σ da proeção a é ua fução do vetor utáro e. = a e σ f 6.9 7
8 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro A KL obetva deterar o couto de vetores e para cua dreção e R a varâca da proeção a é áa. Portato, a KL vara o vetor e o uverso de todas as possíves dreções e R a busca daquela dreção que resulta o áo f e. Para que a ora de e ão flua o resultado de f e durate a busca, ela deve ser costate e utára. Esta é a razão da codção prelar defda e 6.1. Se e alha-se co ua dreção e R do couto X tal que, esta dreção f e resulta e u áo local detro do uverso de busca, etão, devdo à eor declvdade de f e as vzhaças de u áo local, para qualquer pequea varação δ e do vetor utáro e teos que f e e f e +δ 6.1 Nota: Ebora 6.1 tabé sea válda as vzhaças de u ío local, esta abgüdade é plctaete resolvda quado utlza-se a ege-estrutura de C [7]. Cobado as Equações 6.8 e 6.9 obté-se que f e e C e δ e sea sufceteete pequeo de odo que e que o valor de =. Assudo f ão se afaste das vzhaças do áo local, pode-se adtr a gualdade e 6.1. Portato, f e e e = f e + δ e = e + δ e C e + δ e = C 6.11 f e + δ e = e C e + e C δ e + δ e C e + δ e C δ e 6.1 que Coo a atrz de covarâca C do couto X é ua atrz sétrca, te-se e C δe = δe e 6.13 C e a Equação 6.1 pode ser reescrta sob a fora f e δ e = e C e + δ e C e + δ e C δ e
9 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Coo δ e é uto pequeo, o tero δe e C δ o lado dreto de 6.1 pode ser descosderado. De 6.14, 6.8 e 6.9 pode-se escrever que f e δ e = f e + δ e e C Ao levar a Equação 6.1 à Equação 6.15 coclu-se que δ e C e = 6.16 as, para que a ora de e ão flua o resultado de f e durate a busca, ela deve ser atda costate e utára. Portato, são adssíves apeas as perturbações δ e para as quas a ora do vetor perturbado e + δ e peraeça utára, ou sea e + δ e = o que equvale a dzer que e + e e + δ e = 1 Epaddo o produto e δ e e + δ e δ , teos e + e e + δ e = e e + e δe + δe e + δe δe δ 6.19 ode e ode o tero δ e δe e δe = δe e 6. pode ser descosderado. Portato, e + e e + δ e δ = e e + δe e 6.1 coo, de 6.18, δ 1 as, de 6.1, e e = 1 e + δ e e + e = etão, de 6.1 e 6., e portato e e + δe e =1 6. 9
10 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Ifere-se da Equação 6.3 que as varações δ e e = 6.3 δ e deve ser ortogoas a e durate o processo de busca da dreção de áo f e. Este é o úco tpo de varação pertda a e o espaço de busca R tal que a Equação 6.17 sea obedecda. Nas Equações 6.16 e 6.3 resde as duas codções sultâeas a sere respetadas para a deteração dos vetores e para os quas f e terá valor áo. Soado-se estas equações, pode-se escrever que δe e λ δe e = δ e C e λδe e = C 6.4 ode o fator de escala λ fo troduzdo para copatblzar a udade desoal do vetor utáro e adesoal por defção co a udade desoal da atrz represetatva da covarâca do couto X. Por eeplo, se os vetores do couto X C represeta ua gradeza cua udade desoal é etro segudo, λ terá udade desoal etro. segudo Reescrevedo a equação 6.4, δ e e λ e = C 6.5 Para que a codção posta a Equação 6.5 sea satsfeta, é ecessáro e sufcete que C e = λ e 6.6 que é a equação que defe os vetores e para os quas f e te valor áo. A Equação 6.6 é recohecda coo a equação dos auto-vetores da atrz e apreseta u couto de soluções ão-trvas para aqueles valores de λ que são deoados os auto-valores de C. Sea a k-ésa solução de 6.6 tal que C 1
11 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro λ I = C k e k Por sere apeados o vetor ulo através de C λ k I pertece ao espaço ulo da trasforação lear 6.7, sto é, -, os auto-vetores e k N e k R 6.8 ode N R é deoado espaço ulo da atrz C λ k I -, deotado por N { C - λ k I}. A desão N R do espaço ulo de ua trasforação lear defe o úero N de vetores learete depedetes que leva a trasforação ao vetor ulo, os quas, portato, defe ua base geradora de N R [8][9]. O rak da atrz C - λ k I, deotado R { C - λ k I} úero R de vetores-coluas de C λ k I, é o espaço R R gerado pelo - que são learete depedetes. U teorea de eora de atrzes prova que a desão da atrz quadrada C - k I [ ] é gual à soa das desões de seu rak e espaço ulo [8][9], sto é { C - λ k I} N +R = = d 6.9 Por defção, os auto-vetores e k fora ua base ortooral o espaço por eles gerado. Isto sgfca que e 6.7 o couto de auto-vetores e k defe a própra base para o espaço ulo N R. Portato, de 6.9, para que a desão N do espaço ulo sea gual à desão da atrz C λ k I R. Ass = = d{ C - λ k I} = -, é ecessáro que o rak da atrz sea ulo N, de fora que estrão vetores ek learete depedetes. as, ua atrz que possu rak ulo é ua atrz sgular. Isto é, se e, se a atrz C λ I R { C - λ I} = C λ I - é sgular, pode-se escrever que - é sgular, =,1,!, { C λ I} det - = 6.31 λ 11
12 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro ode det {} represeta o deterate da atrz argueto. λ da atrz A Equação 6.31 é a equação utlzada para a deteração do -éso auto-valor C represetatva da covarâca do couto X, =,1,!, 1. Coo C é ua atrz sétrca, possu auto-valores reas e ão-egatvos [8][9]. Ua vez deterados os auto-valores λ λ1,!, 1 da atrz C através de, λ 6.31, obté-se os auto-vetores assocados e,e1,!, e 1 através de 6.7. Ass, de 6.7 pode-se escrever Sea Λ ua atrz dagoal, de acordo co a Equação 6.3, C e = λ e, =,1,!, 1 6.3, coposta pelos auto-valores da atrz C, λ, λ,, λ,! λ Λ = dag 1!, ode os auto-valores estão ordeados de fora decrescete, de odo que λ sea o aor auto-valor. e Sea E ua atrz,e1,, e 1 cuas coluas são foradas pelos auto-vetores! dados pela Equação 6.3 assocados aos auto-valores λ λ1,!, 1. = 1, λ E [ e e! e! e 1 ] 6.34 De acordo co 6.33 e 6.34, a Equação 6.3 pode ser reescrta coo C E = EΛ 6.35 Coo os auto-vetores de C vetores-colua de E são ortooras, a atrz E é dta ortooral. Portato, os vetores-colua de E satsfaze a codção de ortooraldade, e e 1, = 6.36 =, 1
13 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro A Equação 6.36 pode tabé ser escrta sob a fora E E = I 6.37 de ode ve que E 1 = E 6.38 A Equação 6.35 pode ser reescrta, sob a fora de ua rasforação de Slardade [8][9]. Pré-ultplcado abos os lados da Equação 6.35 por ou De 6.39 e 6.38, que, a fora epadda, resulta e E, E C E = E EΛ E C E = E C E = E EΛ 6.4 E C E = Λ 6.41 e C e k λ, =, k = k 6.4 Das Equações 6.8 e 6.9 te-se e = e C e σ = f 6.43 Coparado as Equações 6.4 e 6.43, verfca-se que a f e λ =, =,1,!, Portato, os auto-vetores e da atrz ao logo das quas a varâca = f e C represeta as dreções prcpas σ é áa e dada por λ. 13
14 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro 6..1 Iterpretação Geoétrca da KL A decoposção e sub-espaços gerada pela KL cosste e obter o couto de auto-vetores e auto-valores da atrz de covarâca C de u couto U de éda zero, coposto por L vetores de dados u R, =,1,, L 1!. A restrção de que o couto U apresete éda vetoral R é trasparete a ível de procedeto, á que o vetor éda pode ser restaurado ao fal. O couto de auto-vetores e R obtdo pela KL, =,1,!, 1, defe ua base de vetores ortooras e R e, portato, defe u couto de eos ortogoas Cartesaos. A coordeada de orge deste sstea Cartesao é a coordeada de orge dos vetores da base ortooral defda pelo couto de auto-vetores e. Coo a éda do couto U é assuda zero, a coordeada de orge do sstea Cartesao é vetores u R. Ao proetar o couto orgal de R sobre o -éso eo Cartesao, a varâca do couto proetado ou varâca do sub-espaço é dada pelo -éso auto-valor λ. Ada, a varâca do couto U é gual à soa das varâcas das proeções de U [3][4][5][6]. Isto é, a éda do quadrado da ora Eucldaa dos vetores de U é gual à soa dos auto-valores λ, ode λ equvale à éda do quadrado da ora Eucldaa da proeção dos vetores u R sobre o -éso eo. A título de terpretação da KL, se qusésseos obter a KL através de u processo aual e eperetal, toaríaos u vetor arbtráro de ódulo utáro e R co orge e R, o qual defra ua dreção arbtrára e que o couto U de vetores u R de dados sera proetado. Proetaríaos, etão, a totaldade do couto U sobre a dreção dada por e e edríaos a varâca λ da proeção. Após tetaros todas as dreções possíves o espaço R, haverá ua dreção dada por e a qual é obtda a aor varâca λ. O vetor e que defe tal dreção é gual ao auto-vetor e assocado ao aor auto-valor, obtdos pela KL, co valor do aor auto-valor dado por 14
15 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro λ. O processo é repetdo ovaete para a obteção do segudo aor auto-valor λ 1, co a restrção de que a busca da dreção de aor varâca e R sea feta e dreções ortogoas à do auto-vetor e assocado ao aor auto-valor λ, recé deterados. A busca da dreção de aor varâca e R para obteção do tercero aor auto-valor λ é feta co a restrção de que as dreções testadas sea ortogoas às dreções dos dos auto-vetores e e e 1 assocados aos aores auto-valores λ e λ 1 prevaete ecotrados. E ass prosseguríaos este processo recursvo até que os auto-valores e auto-vetores fosse deterados. Ass, coo os sub-espaços obtdos pela KL estão alhados co as dreções ortogoas de aor varâca possível o espaço orgal R, a KL é cosderada ua trasforação óta o setdo do erro édo quadrátco SE [3][4][5][6][11][7] para efeto de recostrução do espaço orgal R a partr de suas proeções ou copoetes prcpas. Ou sea, o couto de sub-espaços represeta de aera óta, o setdo do SE, o couto U de L vetores u R,,1,, 1 =! L. Cofore á dscutdo, os sub-espaços obtdos pela KL ecotra-se alhados co os eos Cartesaos que defe as dreções de aor varâca possíves o espaço orgal R. E coseqüêca, sto resulta e ua aor cocetração de potos defdos pelos vetores u R do espaço orgal as vzhaças dos eos Cartesaos que defe cada sub-espaço. varâca Coo o -éso eo Cartesao defe a -ésa regão e R de aor λ, aqueles vetores cua éda do quadrado de suas oras Eucldaas é próa ao valor λ λ é a éda do quadrado das oras Eucldaas das proeções destes vetores sobre o -éso eo caracterzarão u sub-couto de vetores do espaço R aproadaete alhados co o -éso eo. Parte destes vetores estará aproadaete cogruete.e., alhados o eso setdo co o -éso se-eo postvo, e parte dos vetores estará aproadaete cogruete co o -éso se-eo egatvo. as, depedeteete do setdo 15
16 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro postvo ou egatvo, a éda do quadrado da ora Eucldaa destes vetores será, e aor ou eor grau, próa ao valor λ, grau que depede do quato os vetores alha-se co o -éso eo Cartesao. Adcoalete, a éda dos vetores que são cogruetes co o se-eo egatvo tede a ser gual à éda dos vetores que são cogruetes co o se-eo postvo, á que U apreseta éda vetoral R. Ass, deve-se esperar u certo equlíbro etre os vetores alhados co cada u dos dos se-eos. Portato, o -éso sub-espaço detfca ua uve de potos e R as vzhaças do -éso eo Cartesao, co coordeada de cada poto defda pelo respectvo vetor u R do couto U as vzhaças do -éso eo. Coo a éda do quadrado da ora Eucldaa dos vetores assocados a estes potos tede e aor ou eor grau para λ, a ora ou dstâca Eucldaa éda destes potos à orge aproa-se do valor λ. Eeplo 6.1: Sea o couto U de L = 6 vetores u R, =,1,, L 1!, de éda zero defdo por U =,,,,, a Plote os auto-vetores e da atrz C de covarâca de U coutaete co os vetores de U. Para facltar a vsualzação, escaloe os auto-vetores e pela raz dos respectvos auto-valores λ,.e., ψ = e λ, =, 1. b Obteha as proeções de U sobre os eos Cartesaos defdos pelos auto-vetores de C. 16
17 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Solução: L C = = L 6 = = = = =.1 = De 6.3, teos C e = λ e sedo =,1,!, 1, co = =, porque u R. A solução de C e = λ e co.1.49 C = cosste a deteração dos auto-valores λ e dos auto-vetores e que satsfaze esta equação. Utlzado as fuções egevals e egevecs do aplcatvo athcad da athsoft Ic., obteos : Auto-valores de C: λ = e λ1 = Auto-vetores de C assocados: e = e e 1 = Nota: Qualquer outro aplcatvo da área de ateátca pode ser utlzado para deterar os auto-valores e auto-vetores de C, coo, por eeplo, o atlab da athworks Ic. 17
18 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro A Fgura 6.1 ostra o couto U, os = auto-vetores escaloados ψ = e λ, =,1,!, 1 e os eos Cartesaos por eles defdos. Fgura 6.1: Couto U, auto-vetores escaloados defdos. ψ e ψ e os eos Cartesaos por eles 1 A abela 6.1 ostra a valor da proeção de cada vetor u R do couto U sobre os eos Cartesaos defdos por e e e 1. 18
19 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro a a u = e 1 u = e abela 6.1: Proeções a e a 1 de U sobre os eos Cartesaos defdos por e e e 1. Observe que, coo os auto-vetores e e e 1 tê ora utára e são adesoas [8], o valor absoluto da proeção de cada Eucldaa da -ésa proeção. u R sobre cada eo defe a ora Note que a varâca do couto U é dada pela soa dos auto-valores,.e., 1 L L = 1 u = 1.15 = λ + λ 1, ode u u = u u = = 1 é a ora Eucldaa do vetor u R [8]. Note ada que as varâcas das proeções a e a 1 de U equvale aos respectvos auto-valores,.e., u e = = λ 1 L L = 1 e 1 L 1 L = 3 u e1 = = λ1 varâca do sub-espaço, é dada pelo -éso auto-valor λ.. Portato, a varâca do couto proetado, ou 1 1 L Coo observação adcoal ote que a dstâca Eucldaa éda L = u e dos vetores da -ésa proeção à orge pode ser aproada por 1 L L 1 = u e = λ 1 1 L. No caso, L = u e = para λ = e 1 1 L L = u e1 =. 78 para λ 1 =
20 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro 6.. O Processo de Copressão Possbltado pela KL Na seção ateror vos que os eos Cartesaos resultates da KL alha-se co as dreções de aor varâca =eerga de u couto U de vetores R desoas, sedo =. dados e R o vetor éda de U. O Eeplo 6.1 lustrou u caso para A Fgura 6. ostra ua represetação pctórca hpotétca de ua uve de 3 R. Cada poto da uve defe a pota de u vetor deste couto U e A fgura ostra a aera coo a base ortooral forada pelos auto-vetores alha-se co as dreções de aor varâca eerga de U. Ass, o caso geérco de u 3 R. couto U e R, podeos agar a KL "grado" ua base de vetores ortooras e R e todas as possíves dreções até que os vetores alhe-se co as dreções de aor varâca possível e U. Nesta stuação os vetores da base ortooral são os auto-vetores da atrz de covarâca de U. Fgura 6.: Represetação pctórca hpotétca de ua "uve" de dados e R 3 e a aera coo a base ortooral forada pelos auto-vetores e, e 1 e e alha-se co as dreções de aor varâca.
21 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Vos tabé que a eerga cotda e ua deterada dreção =varâca da proeção de U a dreção é dada pelo auto-valor assocado ao auto-vetor que defe a dreção. Portato, podeos desprezar aquelas dreções =sub-espaços defdas por auto-vetores cuo auto-valor assocado é uto eor do que os deas auto-valores. Isto é possível porque a proeção de U sobre tas dreções é sgfcate se coparada co as proeções cuo auto-valor assocado ão é coparatvaete pequeo. Ao desprezar sub-espaços de eor eerga estaos realzado ua copressão co perdas do couto U. No etato estas perdas são ías pos as copoetes =sub-espaços descartadas te pouca fluêca a foração de U porque os auto-valores a elas assocados supostaete tê valor uto eor do que os deas. Neste setdo ocorre a redução desoal de U, porque o couto era orgalete represetado e R e, ao descartar sub-espaços ão sgfcatvos, o couto passa a ser represetado co boa aproação e ua desão eor que. Este é o otvo de a KL ser cosderada ua trasforação óta sob o poto de vsta do SE. Eeplo 6.: Sea o couto U do Eeplo 6.1. a Eecute ua copressão co perdas de U utlzado a KL. b Calcule a copressão obtda. c Calcule o SE da copressão obtda. d Calcule a Relação Sal Ruído de Pco e db, deotada PSNR PSNR Peak Sgal o Nose Rato, resultate do processo de copressão. Isto é, calcule o quadrado da copoete de aor valor absoluto detre todas as copoetes dos vetores de U e oralze pelo SE obtdo e c. 1
22 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Solução: No Eeplo 6.1 fora deteradas as proeções de U sobre a base ortooral forada pelos auto-vetores e e e 1, cofore ostra a abela 6.1. Observe a abela 6.1 que as proeções sobre a dreção e 1 são uto eores do que as proeções sobre a dreção e. Esta característca das proeções está de acordo co o fato de que 3 λ 7.35 é uto eor do que λ = 1 = 1.. Sedo ass, podeos descartar as proeções ou copoetes de U a dreção e 1 a dreção co eor auto-valor assocado e cosderar as proeções de U a dreção e a dreção co aor auto-valor assocado coo ua boa aproação de U. Portato a copressão co perdas cosste e aproar U através do auto-vetor e e do couto de proeções a = u e a dreção por ele defda. A aproação U ~ do couto de vetores orgas u U, é obtda através de u~ = a e, u ~ U ~, sto é, a e = u e, = u ~ = a e abela 6.: Aproação U ~ do couto orgal U obtda através de u~ = a e, ode u ~ U ~. Portato, da abela 6., o couto U ~ resultate é ~ U =,,,,,
23 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Observe que o couto orgal U =,,,,, de L = 6 vetores para ser represetado. u R, =,1,, L 1! ecessta de 1 úeros e poto-flutuate Por outro lado, o couto aproado U ~ fo gerado a partr do auto-vetor e de u couto de 6 proeções = { 1. 14, 1. 17,. 9,. 953, 1. 34,. 964} e.47 =.94 a. Portato, o couto U ~ represetado. ecessta de apeas 8 úeros e poto-flutuate para ser ρ = Defe-se coo fator de copressão ρ o quocete otal de udades de arazeaeto ecessáro para otal de udades de arazeaeto ecessáro para ~ represetar U represetar U 6.45 Portato o fator de copressão obtdo é ρ = 8 1 =. 67. O SE da aproação U ~ pode ser obtdo através de 1 SE = u~ u u~ u 6.46 L L 1 = ode u U e u ~ U ~, =,1,!, L 1. De 6.46 obteos 3 SE. = A PSNR é defda coo PSNR = 1log a cop{} U SE 6.47 sedo a cop{} U a copoete de aor valor absoluto detre todas as copoetes dos vetores de U. De 6.47 obteos PSNR = 1log = db. 3
24 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Eeplo 6.3: Obteha o couto de vetores u ~ U ~ a partr de todos os sub-espaços do couto de vetores u U do Eeplo 6..e., ão eecute ehua copressão, apeas recostrua o couto orgal a partr de abos sub-espaços a e a 1. Detere a PSNR do couto recostruído U ~. Solução: A partr da abela 6.1 obteos a abela 6.3 abao. a a e = u e, = 1 = u e1, 1 =.94 e u ~ = a a e e abela 6.3: Recostrução U ~ do couto orgal U obtda através de u~ = a e a e, ode u ~ U ~. Coo ehu sub-espaço é descartado, ehua copressão é obtda e o couto U ~ é cosderado ua recostrução do couto orgal U a partr dos sub-espaços a e a 1. Da abela 6.3 obteos, ~ U =,,,,, De 6.46 obteos 7 SE. = E, de 6.47 obteos PSNR = 1log = db. 4
25 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Nota: Observe que o SE ão é zero e portato a PSNR ão é fta ucaete devdo à precsão 3 casas após a vírgula as operações de poto-flutuate efetuadas. Se estvésseos trabalhado co ua precsão sufcete o SE sera zero porque este eeplo, ao cotráro do Eeplo 6., ehua foração é descartada. Aqu o couto orgal U é apeas recostruído a partr de todos os seus sub-espaços se ocorrer qualquer copressão Copressão de Iages através da KL Nesta seção estudareos coo efetuar a copressão de ages através da KL [3][4][5][6]. Por splcdade trabalhareos co ages e tos de cza grayscale. Ua age e grayscale te seus valores de pel varado etre e 55. O valor represeta preto e o valor 55 represeta braco. odos os deas valores teredáros represeta tos de cza. A toaldade cza de u pel de ua age grayscale clarea à edda que o valor do pel aueta. A Fgura 6.3 ostra a age grayscale Lea de taaho pels. Fgura 6.3: Iage grayscale Lea de taaho pels. 5
26 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Para coprr a age da Fgura 6.3 através da KL, adotareos o segute procedeto: 1 Subdvde-se a age e L = 56 blocos de 8 8 pels e regstra-se a posção de cada bloco a age p/ certas ages, elhor resultado é obtdo c/ blocos O -éso bloco B de 8 8 pels é covertdo e u vetor R desoal U u, sedo = 64 devdo ao bloco possur 8 8 pels, =,1,!, L 1. A coversão bloco-vetor B u é efetuada ledo-se as 8 lhas de B da esquerda para a dreta sedo a lha ao alto a prera a ser lda e trasferdo o valor de cada pel ldo esta orde para as respectvas posções e seqüêca o vetor u. 3 Calcula-se o vetor éda do couto de vetores U obtdo e e subtra-se este vetor éda de todos os L = 56 vetores u U. 4 Detera-se os sub-espaços de U cofore á dscutdo a Seção Descarta-se aqueles sub-espaços assocados aos eores auto-valores. 6 ~ Obté-se o couto de vetores u ~ U sedo u ~ a e + a1 e1 +! + a 1 e, ode 1 = N N { a, a,!, a } são os sub-espaços defdos pelos auto-vetores { e e,, e } 1 N 1,! cuos 1 N 1 auto-valores assocados são os N aores auto-valores os N sub-espaços de aor eerga. N é obtdo eperetalete e defe o coprosso etre ρ e PSNR. 7 ~ Soa-se ao couto de L vetores u ~ U o vetor éda orgalete subtraído de U. 8 Obté-se o couto de blocos B ~ através da coversão bloco-vetor versa u~ B ~, =,1,!, L 1, e reota-se a age coprda a partr do regstro da posção de cada bloco. 6
27 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro A Fgura 6.4 ostra a apltude relatva e orde decrescete dos 3 preros aores auto-valores do couto U forado a partr da Fgura 6.3 de acordo co o procedeto aca descrto. Fgura 6.4: Apltude relatva e orde decrescete dos 3 preros aores auto-valores do couto U forado a partr da Fgura 6.3. Observe que o úero total de 64 auto-valores é 64, á que cada vetor de U é de desão R. No etato, vsto que aproadaete a partr do vgéso aor auto-valor a apltude relatva tora-se pequea, escolheu-se represetar apeas as 3 preras aores apltudes. A Fgura 6.5 ostra a age coprda resultate forada a partr dos 3 preros sub-espaços de aor varâca e a Fgura 6.6 ostra a age coprda resultate forada a partr dos 16 preros sub-espaços de aor varâca. 7
28 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Fgura 6.5: Iage da Fgura 6.3 coprda pela KL utlzado os N = 3 preros sub-espaços de aor eerga. O coefcete de copressão resultate é ρ =. 69 Equação A fdeldade da age coprda co relação à orgal é dada por PSNR = db Equação Fgura 6.6: Iage da Fgura 6.3 coprda pela KL utlzado os N = 16 preros sub-espaços de aor eerga. O coefcete de copressão resultate é ρ =. 316 Equação A fdeldade da age coprda co relação à orgal é dada por PSNR = db Equação
29 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro 6.3 O Algorto Hebbao Geeralzado para PCA ou DSE de u Espaço Vetoral Cofore estudaos a Seção 6. deste capítulo, para proceder à Aálse dos Copoetes Prcpas ou Decoposção de u Espaço Vetoral e Sub-Espaços é ecessáro coputar a atrz de covarâca do couto de dados de etrada para, etão, aplcar u procedeto uérco que etraa os auto-valores e os correspodetes autovetores desta atrz. Os auto-vetores correspodetes aos auto-valores as sgfcatvos são usados para etrar os copoetes prcpas dos dados. No etato, para grades coutos de dados, as desões da atrz covarâca cresce sgfcatvaete, torado este étodo adequado para a etração dos copoetes prcpas. Alé dsto, todos os auto-valores e auto-vetores precsa ser coputados, eso que soete poucos auto-vetores aqueles correspodetes aos aores auto-valores veha a ser utlzados o processo. A solução efcete para este problea deve ecotrar os prcpas auto-vetores se a ecessdade de deterar a atrz covarâca. al solução é alcaçada ao abordar o problea utlzado Redes Neuras Artfcas [15]. A técca que utlza RNAs para efetuar a Aálse dos Copoetes Prcpas sobre u espaço vetoral de teresse a ser abordada este estudo é deodada "Algorto Hebbao Geeralzado" e fo proposta por Sager e 1989 [7]. Este algorto coba a ortooralzação de Gra-Schdt [14] ao odelo de u úco eurôo lear troduzdo por Oa e 198 [7]. O Algorto Hebbao Geeralzado deoado GHA a lteratura é u dos algortos as usados e aplcações prátcas, porque:! etra os copoetes prcpas dvdualete, u após o outro, e orde decrescete de varâca e 9
30 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro! porque possblta que, após treada a rede, os resultados obtdos possa ser aplcados a u outro couto de dados de estatístca "seelhate" ou sea, que resulte e ua atrz de covarâca "seelhate" [7]. O desevolveto apresetado este capítulo segue a eposção de Hayk e [7], Hassou e [11] e Hertz, Krogh e Paler e [15] O Apredzado Hebbao Na Seção 6.1 estudaos os prcípos que rege o apredzado auto-orgazado, sprados o postulado de apredzado de Hebb. O Apredzado Hebbao é ua classe de apredzado ão-supervsoado ou autoorgazado, e que os parâetros lvres da rede são adaptados pela eposção da RNA ao abete e que está cotda, até que ua pré-deterada codção sea atgda, através: " da repetção dos padrões de etrada por u úero sufcete de vezes e " da aplcação de u couto de regras de apredzado uto específcas, adequadas à solução do problea. Ua RNA treada sob apredzado ão-supervsoado descobre padrões sgfcatvos ou característcos dos dados de etrada se o auílo de u tutor etero. Ou sea, ão há realetação do abete para aular a rede a deterar se a saída está ou ão correta. A RNA deve descobrr por s padrões, característcas, regulardades, correlações ou categoras os dados de etrada. As udades e coeões deve, portato, apresetar algu grau de auto-orgazação. E algus casos, os vetores de etrada pode ser apeados e u couto desoalete eor de padrões, tal que este couto de padrões preserve as relações estetes o couto orgal. 3
31 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro O coheceto que va sedo crstalzado a RNA é obtdo da observação repetda de parâetros estatístcos éda, varâca e atrz correlação dos dados de etrada. Neste setdo, redudâca de padrões provê coheceto. Na rede de ua úca udade, ostrada a Fgura 6.7, os sas pré-sáptcos e pós-sáptcos, respectvaete e y, pode ser equacoados por y + 1 = + η y 6.48 = = 6.49 ode η é ua costate postva que detera a razão de apredzado, é o vetor de etrada da rede e y é a saída da rede. Fgura 6.7: RNA de ua úca udade, a ser treada pelo Apredzado Hebbao. Observe que a Equação 6.48 epressa a udaça o peso sáptco, que ocorre a proporção da correlação etre os sas pré e pós-sáptcos, equato que a Equação 6.49 epressa a saída da RNA. 31
32 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro O couto de vetores de etrada possu dstrbução de probabldade arbtrára. A cada tepo u vetor é apresetado à rede, escolhdo aleatoraete do couto. Cofore vos a Seção 6.1, segudo os prcípos do Apredzado Hebbao: I II quato as provável for ua partcular etrada, aor será a correlação da saída y co esta etrada. Ass, quato as provável for, aor será a saída y; quato aor for a saída y, as a varação do peso sáptco que a ecoraou auetará. As afrações I e II ada as são do que o 1º prcípo da auto-orgazação de vo der alsburg: "odfcações e pesos sáptcos tede a se auto-aplfcar". Ou sea: a correlação etre as udaças os pesos sáptcos e as udaças os padrões de atvdade deve ser postva para que se obteha auto-orgazação da rede; o processo de auto-aplfcação é restrto pelo requereto de que odfcações e pesos sáptcos deve ser baseadas e sas sas pré-sáptcos e pós-sáptcos dspoíves localete; ua forte sapse coduz à cocdêca de sas pré e pós-sáptcos e, por outro lado, a sapse é auetada e força, por tal cocdêca. Ou, ada, segudo o postulado de Hebb: Se dos eurôos e cada lado de ua sapse são atvados sultaeaete, etão a força daquela sapse é seletvaete auetada. O "loop" cofgurado por I e II, o etato, fara co que os pesos sáptcos peraecesse crescedo se lte, peddo a cotuação do processo de apredzado e levado o odelo à stabldade. Na realdade, o que ocorre é que, pelo aueto deasado do peso sáptco, a rede é levada à saturação precoce e é capaz de apreder os padrões apresetados. 3
33 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro Sabeos, através do º prcípo da auto-orgazação de vo der alsburg "Ltação de recursos coduz à copetção etre as sapses e, coseqüeteete, à seleção das sapses que cresce de fora as vgorosa portato, as as adequadas às custas de outras", que precsa ser estabelecda algua fora de copetção por recursos "ltados", para que o sstea possa ser establzado. A solução cosste e copesar o aueto a força de algua sapse a rede, pelo decrésco e outras, para que apeas as sapses que obtê sucesso possa crescer, equato outras efraqueça e, evetualete, desapareça. O problea de establdade do odelo pode ser vestgado cofore segue: Supohaos que, após u tepo de apredzado sufceteete grade, os pesos sáptcos ata u poto de equlíbro. oado-se o valor esperado da udaça dos pesos sáptcos de acordo co a Equação 6.48 para esta suposta codção de equlíbro, E } = E{ η y } 6.5 { Substtudo a Equação 6.49 a Equação 6.5, E } = E{ η } 6.51 { Cosderado que o parâetro razão de apredzado η é ua etdade deterístca e que os vetores de dados e os vetores pesos sáptcos são estatstcaete depedetes, E } =η E{ } E{ } 6.5 { E que, o equlíbro, E { } =, 6.53 { } C e 6.54 E = E { } = e,
34 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro pos, para ua codção de equlíbro, o úero de terações sera sufceteete grade para que o vetor de pesos sáptcos tedesse a u valor costate valor de equlíbro. Ou sea, quado, e, ode e é u valor costate. Nestas codções, a Equação 6.5 se tora C e = 6.56 Ass, o suposto poto de equlíbro, a solução da Equação 6.56 cofore a teora de auto-valores e auto-vetores é u auto-vetor e de C cuo correspodete autovalor é zero. Alguas cosderações pode ser traçadas a partr da Equação 6.56: # a atrz de correlação C é ua atrz Hertaa, que é sepre ão-ula, pos deota a correlação do sal co ele própro eso u sal de ruído te autocorrelação ão ula; # os auto-valores de ua atrz Hertaa são reas e poderão ser postvos. Qualquer flutuação de u peso sáptco que teha ua copoete ao logo da dreção de u auto-vetor assocado a u auto-valor postvo crescerá epoecalete. Ass, a dreção relatva ao aor auto-valor da atrz covarâca poderá se torar doate, de fora que o peso sáptco rá se aproar gradualete de u autovetor e correspodete a u auto-valor áo, cua ora crescerá deasadaete. O auto-vetor e, portato, uca se establzará e haverá soete soluções stáves para o algorto de Apredzado Hebbao. 34
35 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro O problea da stabldade do algorto, aca eposto, pode ser equacoado da segute fora: Ao toar a dervada da varação do peso sáptco e relação ao própro peso sáptco, podereos vestgar de que fora a varação do peso sáptco se coporta ao logo do tepo. Ass, d d d = η y d 6.57 Cosderado as foras epaddas a Equação 6.57, d d = d η d 6.58 A dervada do soatóro da epressão 6.58 e relação a só estrá para o tero, quado será gual a. A Equação 6.58 se torará, portato, d d =η 6.59 De acordo co a Equação 6.59, a razão de varação da varação do peso sáptco é postva para todo e todo p. Isto plca que, ao logo de todo o processo de atualzação dos pesos sáptcos, a varação será crescete, o que tora o auto-vetor e ua solução stável para o algorto. Solução proposta por Oa para o problea da stabldade do algorto: Para evtar a dvergêca do algorto de apredzado Hebbao é precso restrgr o cresceto do vetor. Oa propôs e 198 [7] coo ua alteratva para a 35
36 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro establzação do Apredzado Hebbao, ua odfcação o algorto que perte ao vetor peso sáptco atgr ora utára, alé de correspoder ao aor auto-valor de C. A regra de Oa correspode a adcoar u decaeto ao peso sáptco, proporcoal a y. A Equação 6.6 epressa ovaete sob a fora vetoral a regra de Apredzado Hebbao, após deflacoada de u fator η y. + 1 = +η y η y 6.6 A regra deflacoada para o Apredzado Hebbao apresetada a Equação 6.6 pode ser reescrta coo, = η y { y } 6.61 Para provar que = 1 e que o peso sáptco está depostado a dreção do aor auto-vetor de C, cosdere-se a Equação oado o valor esperado da udaça dos pesos sáptcos, y E } = E{ η y [ y ]} 6.6 { Reescrevedo a Equação 6.6, E } = E{ η [ y y y ]} 6.63 { Cosderado que η é ua etdade deterístca e levado a Equação 6.49, = =, à Equação 6.63, E{ } = η E{ } 6.64 o equlíbro, Cosderado ada que os vetores e são estatstcaete depedetes e que, 36
37 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro A Equação 6.64 se tora, E { } =, 6.65 E { } = e e 6.66 { } C 6.67 E = e C e = C e e Ass, u vetor o equlíbro deve obedecer a C e = e C e e Cofore vsto a Seção 6. e que estudaos a KL para PCA ou DSE de u Espaço Vetoral, de acordo co a Equação 6.4, e k = C C e = λ para k e e e = para k k Ass, e a Equação 6.69 pode ser reescrta coo, e de e e C e = λ 6.7 C e = λ e 6.71 A aálse da Equação 6.71 ostra que, o equlíbro, deve ser o auto-vetor C. Pré-ultplcado abos os lados da gualdade epressa a Equação 6.71 por pode-se escrever que, e C e = e λ e 6.7 À esquerda do sal de gualdade vê-se claraete a Equação 6.7. Alé dsto, coo, à dreta da gualdade, λ é u escalar e 37
38 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro e = e e 6.73 ode e é a ora Eucldaa do vetor e, pode-se afrar que λ = = λ e e λ e 6.74 de ode coclu-se que o valor covergdo e do vetor peso sáptco te ora utára, cofore pretedíaos ostrar. Há p possíves auto-vetores da atrz C que satsfaze à codção da Equação 6.71, o etato, apeas o auto-vetor e, correspodete ao aor auto-valor λ = λ a, represeta ua solução estável. Deostreos, agora, que a solução represetada pelo auto-vetor assocado ao aor auto-valor é a solução estável: Cosdere-se que, após u grade úero de terações, o peso sáptco estea a vzhaça de u vetor e tal que, = e + ε, 6.75 ode ε é u vetor pequeo que represeta a dstâca do peso sáptco ao auto-vetor. Partdo da Equação 6.64 ode toou-se o valor esperado da varação dos pesos sáptcos e cosderado as codções epressas pelas Equações 6.65, 6.66, 6.67 e 6.68, ecotra-se E { } = η { C e + ε e + ε C e + ε e + ε}, 6.76 Efetuado as operações à dreta da gualdade a Equação 6.76, cosderado a codção de setra da atrz Hertaa C e desprezado os teros de seguda orde 38
39 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro e de ordes aores e ε, é possível aproar o valor esperado toado e 6.76 para prera orde e ε por E { } η { C e + C ε e C e e ε C e e e C e ε }, Ua vez que e é u auto-vetor da atrz de correlação 6.77 C, pode-se escrever que C e = λ e, =1,,..., p e e 1, = e =,, a Equação 6.77 pode ser reescrta a fora splfcada E{ } η{ C ε λ ε e e λ ε } ou, E{ } η { C ε λ e e ε λ ε } 6.81 ode cosderou-se que ε e é u escalar e que este produto tero tabé pode ser epresso coo e ε. A udaça éda o vetor peso sáptco, proetada sobre a coordeada represetada por outro auto-vetor E{ } por e. Desta fora, e da atrz C é obtda pré-ultplcado e E{ } η { e C ε λ e e e ε λ e ε } 6.8 ou, cosderado as Equações 6.78 e 6.79 e a propredade de setra de C, 39
40 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro e η λ e ε, E{ } η λ λ e ε, = 6.83 A aálse da Equação 6.83 perte coclur que: $ para =, A proeção do valor esperado da varação do peso sáptco a dreção do própro auto-vetor assocado é sepre egatva. Portato, coo a varação do peso sáptco é sepre cotrára à dstâca ε, a solução é estável e todas as possíves dreções. $ para, A proeção do valor esperado da varação do peso sáptco assocado ao auto-vetor a dreção de u outro auto-vetor p qualquer soete é egatva se λ > λ. Portato, a varação do peso sáptco será cotrára à dstâca ε, dcado ua solução estável, se e soete se o auto-valor assocado ao auto-vetor for aor do que todos os deas auto-valores correspodetes a outras dreções. 4
41 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro 41 O problea da stabldade do algorto após a corporação da Regra de Oa ou sea, após a regra de Apredzado Hebbao ter sdo deflacoada de u fator y η pode ser ass equacoado: Adotado procedeto seelhate ao utlzado o caso da regra ão deflacoada: Ao toar a dervada da varação do peso sáptco e relação ao própro peso sáptco, podereos vestgar de que fora a varação do peso sáptco se coporta ao logo do tepo. Ass, y y d d d d = η 6.84 Cosderado as foras epaddas, a Equação 6.84, = d d ]} ][ [ { = d d η 6.85 oado a dervada, = d d ] ][ - + [ ] - ][ [ + = η η 6.86
42 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro 4 Dstrbudo os produtos ostrados e 6.86, = d d + = ] - +[ ] - [ η η η η 6.87 Ass, a dervada da varação do peso sáptco e relação ao própro peso sáptco pode ser epressa por = d d - = η η η 6.88 % A observação da Equação 6.88 ão as perte afrar que a dervada será sepre postva, coo e % Portato, a varação da varação do peso sáptco ão é as sepre postva. % A covergêca do algorto ocorre se os valores de e são tas que a Equação 6.88 resulta e u valor egatvo.
43 PUCRS - FENG - DEE - estrado e Egehara Elétrca Redes Neuras Artfcas Ferado César C. de Castro e ara Crsta F. de Castro De acordo co o desevolveto segudo, podeos agora afrar que:! u úco eurôo lear subetdo à regra Hebbaa de apredzado auto-orgazado tede a etrar a prera copoete prcpal do espaço vetoral de dados de etrada [16],! copoete esta que correspode ao aor auto-valor da atrz de covarâca dos dados de etrada O Algorto Hebbao Geeralzado A geeralzação do algorto apresetada esta seção segue a proposta de Sager 1989 e [7] e é obtda a partr do Algorto Hebbao establzado pela Regra de Oa. O processo de geeralzação cosste e aplcar as regras propostas por Sager e Oa a ua RNA progressva, coposta ão as por u úco eurôo lear cofore Fgura 6.7 e, s, por ua caada de eurôos leares, cofore ostra a Fgura 6.8. Fgura 6.8: RNA progressva co ua úca caada de eurôos leares, a ser treada pelo Apredzado Hebbao Geeralzado. 43
16 - PROBLEMA DO TRANSPORTE
 Prof. Volr Wlhel UFPR TP05 Pesqusa Operacoal 6 - PROBLEMA DO TRANSPORTE Vsa zar o custo total do trasporte ecessáro para abastecer cetros cosudores (destos) a partr de cetros forecedores (orges) a, a,...,
Prof. Volr Wlhel UFPR TP05 Pesqusa Operacoal 6 - PROBLEMA DO TRANSPORTE Vsa zar o custo total do trasporte ecessáro para abastecer cetros cosudores (destos) a partr de cetros forecedores (orges) a, a,...,
Balanço de Massa e Energia Aula 2
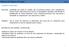 alaço de assa e Eerga ula Udades e Desão Desão: Quatdade que pode ser edda, são as gradezas báscas coo copreto, assa, tepo, teperatura etre outras, ou quatdades calculadas pela dvsão ou ultplcação de outras
alaço de assa e Eerga ula Udades e Desão Desão: Quatdade que pode ser edda, são as gradezas báscas coo copreto, assa, tepo, teperatura etre outras, ou quatdades calculadas pela dvsão ou ultplcação de outras
3- Autovalores e Autovetores.
 MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 3- Autovalores e Autovetores. 3.- Autovetores e Autovalores de ua Matrz. 3.- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. 3.- Autovetores
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 3- Autovalores e Autovetores. 3.- Autovetores e Autovalores de ua Matrz. 3.- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. 3.- Autovetores
3- Autovalores e Autovetores.
 MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS - Autovalores e Autovetores..- Autovetores e Autovalores de ua Matrz..- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. Cotuação da
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS - Autovalores e Autovetores..- Autovetores e Autovalores de ua Matrz..- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. Cotuação da
CAPÍTULO III. Aproximação de funções pelo método dos Mínimos Quadrados
 Métodos Nuércos CAPÍULO III C. Balsa & A. Satos Aproxação de fuções pelo étodo dos Míos Quadrados. Algus cocetos fudaetas de Álgebra Lear Relebraos esta secção algus cocetos portates da álgebra Lear que
Métodos Nuércos CAPÍULO III C. Balsa & A. Satos Aproxação de fuções pelo étodo dos Míos Quadrados. Algus cocetos fudaetas de Álgebra Lear Relebraos esta secção algus cocetos portates da álgebra Lear que
MODELAGEM MATEMÁTICA E ANÁLISE DO PROCESSO DE FLOCULAÇÃO EM CÂMARAS EM SÉRIE
 MODELAGEM MATEMÁTICA E ANÁLISE DO POCESSO DE FLOCULAÇÃO EM CÂMAAS EM SÉIE odrgo B Moruzz, Sauel Coceção de Olvera Professor da Uesp, Capus de o Claro, o Claro-SP, Brasl, roruzz@rcuespbr Professor da Uesp,
MODELAGEM MATEMÁTICA E ANÁLISE DO POCESSO DE FLOCULAÇÃO EM CÂMAAS EM SÉIE odrgo B Moruzz, Sauel Coceção de Olvera Professor da Uesp, Capus de o Claro, o Claro-SP, Brasl, roruzz@rcuespbr Professor da Uesp,
IND 1115 Inferência Estatística Aula 9
 Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Capitulo 7 Resolução de Exercícios
 FORMULÁRIO Audades Costates Postecpadas HP C [g][end] Cp LN 1 1 1 1 C p R Cp R R a, R C p, 1 1 1 a LN 1 Sp LN 1 1 1 S p R S p R R s, R S p, 1 1 s LN 1 Audades Costates Atecpadas HP C [g][beg] 1 (1 ) 1
FORMULÁRIO Audades Costates Postecpadas HP C [g][end] Cp LN 1 1 1 1 C p R Cp R R a, R C p, 1 1 1 a LN 1 Sp LN 1 1 1 S p R S p R R s, R S p, 1 1 s LN 1 Audades Costates Atecpadas HP C [g][beg] 1 (1 ) 1
Capítulo 2. Aproximações de Funções
 EQE-358 MÉTODOS NUMÉRICOS EM ENGENHARIA QUÍMICA PROFS. EVARISTO E ARGIMIRO Capítulo Aproações de Fuções Há bascaete dos tpos de probleas de aproações: ) ecotrar ua fução as sples, coo u polôo, para aproar
EQE-358 MÉTODOS NUMÉRICOS EM ENGENHARIA QUÍMICA PROFS. EVARISTO E ARGIMIRO Capítulo Aproações de Fuções Há bascaete dos tpos de probleas de aproações: ) ecotrar ua fução as sples, coo u polôo, para aproar
Representação dos padrões. Tipos de atributos. Etapas do processo de agrupamento. 7.1 Agrupamento clássico. 7. Agrupamento fuzzy (fuzzy clustering)
 7. Agrupaeto fuzzy (fuzzy clusterg) 7. Agrupaeto clássco Agrupaeto é a classfcação ão-supervsoada de padrões (observações, dados, objetos, eeplos) e grupos (clusters). Itutvaete, padrões seelhates deve
7. Agrupaeto fuzzy (fuzzy clusterg) 7. Agrupaeto clássco Agrupaeto é a classfcação ão-supervsoada de padrões (observações, dados, objetos, eeplos) e grupos (clusters). Itutvaete, padrões seelhates deve
MA12 - Unidade 4 Somatórios e Binômio de Newton Semana de 11/04 a 17/04
 MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
Perguntas Freqüentes - Bandeiras
 Pergutas Freqüetes - Baderas Como devo proceder para prestar as formações de quatdade e valor das trasações com cartões de pagameto, os casos em que o portador opte por lqudar a obrgação de forma parcelada
Pergutas Freqüetes - Baderas Como devo proceder para prestar as formações de quatdade e valor das trasações com cartões de pagameto, os casos em que o portador opte por lqudar a obrgação de forma parcelada
Capítulo 1: Erros em cálculo numérico
 Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
FINANCIAMENTOS UTILIZANDO O EXCEL
 rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: Prof. Lorí Val, Dr. val@pucrs.br http://www.pucrs.br/famat/val www.pucrs.br/famat/val/ correlacoal ou expermetal. Numa relação expermetal os valores
É o grau de assocação etre duas ou mas varáves. Pode ser: Prof. Lorí Val, Dr. val@pucrs.br http://www.pucrs.br/famat/val www.pucrs.br/famat/val/ correlacoal ou expermetal. Numa relação expermetal os valores
UERJ CTC IME Departamento de Informática e Ciência da Computação 2 Cálculo Numérico Professora Mariluci Ferreira Portes
 UERJ CTC IE Departameto de Iormátca e Cêca da Computação Udade I - Erros as apromações umércas. I. - Cosderações geras. Há váras stuações em dversos campos da cêca em que operações umércas são utlzadas
UERJ CTC IE Departameto de Iormátca e Cêca da Computação Udade I - Erros as apromações umércas. I. - Cosderações geras. Há váras stuações em dversos campos da cêca em que operações umércas são utlzadas
Análise de Regressão
 Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
M = C( 1 + i.n ) J = C.i.n. J = C((1+i) n -1) MATEMÁTICA FINANCEIRA. M = C(1 + i) n BANCO DO BRASIL. Prof Pacher
 MATEMÁTICA 1 JUROS SIMPLES J = C.. M C J J = M - C M = C( 1 +. ) Teste exemplo. ados com valores para facltar a memorzação. Aplcado-se R$ 100,00 a juros smples, à taxa omal de 10% ao ao, o motate em reas
MATEMÁTICA 1 JUROS SIMPLES J = C.. M C J J = M - C M = C( 1 +. ) Teste exemplo. ados com valores para facltar a memorzação. Aplcado-se R$ 100,00 a juros smples, à taxa omal de 10% ao ao, o motate em reas
Capítulo 6 - Centro de Gravidade de Superfícies Planas
 Capítulo 6 - Cetro de ravdade de Superfíces Plaas 6. Itrodução O Cetro de ravdade (C) de um sóldo é um poto localzado o própro sóldo, ou fora dele, pelo qual passa a resultate das forças de gravdade que
Capítulo 6 - Cetro de ravdade de Superfíces Plaas 6. Itrodução O Cetro de ravdade (C) de um sóldo é um poto localzado o própro sóldo, ou fora dele, pelo qual passa a resultate das forças de gravdade que
Econometria: 4 - Regressão Múltipla em Notação Matricial
 Ecoometra: 4 - Regressão últpla em Notação atrcal Prof. arcelo C. ederos mcm@eco.puc-ro.br Prof. arco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo
Ecoometra: 4 - Regressão últpla em Notação atrcal Prof. arcelo C. ederos mcm@eco.puc-ro.br Prof. arco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo
A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: enchentes
 Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
Requisitos metrológicos de instrumentos de pesagem de funcionamento não automático
 Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
Matemática. Resolução das atividades complementares. M18 Noções de Estatística
 Resolução das atvdades complemetares Matemátca M8 Noções de Estatístca p. 3 (UFRJ) Dos estados do país, um certo ao, produzem os mesmos tpos de grãos. Os grácos de setores lustram a relação etre a produção
Resolução das atvdades complemetares Matemátca M8 Noções de Estatístca p. 3 (UFRJ) Dos estados do país, um certo ao, produzem os mesmos tpos de grãos. Os grácos de setores lustram a relação etre a produção
DINÂMICA VIBRAÇÕES DE SISTEMAS COM 1 GRAU DE LIBERDADE. António Araújo Correia
 DINÂMICA VIBRAÇÕES DE SISTEMAS COM GRAU DE IBERDADE Atóo Araújo Correa Jaero de 007 VIBRAÇÕES DE SISTEMAS COM GRAU DE IBERDADE. INTRODUÇÃO Esta publcação desta-se ao apoo das aulas da dscpla seestral de
DINÂMICA VIBRAÇÕES DE SISTEMAS COM GRAU DE IBERDADE Atóo Araújo Correa Jaero de 007 VIBRAÇÕES DE SISTEMAS COM GRAU DE IBERDADE. INTRODUÇÃO Esta publcação desta-se ao apoo das aulas da dscpla seestral de
Departamento de Informática. Modelagem Analítica. Modelagem Analítica do Desempenho de Sistemas de Computação. Disciplina: Medida de Probabilidade
 Departaento de Inforátca Dscplna: do Desepenho de Ssteas de Coputação Medda de Probabldade Prof. Sérgo Colcher colcher@nf.puc-ro.br Teora da Probabldade Modelo ateátco que perte estudar, de fora abstrata,
Departaento de Inforátca Dscplna: do Desepenho de Ssteas de Coputação Medda de Probabldade Prof. Sérgo Colcher colcher@nf.puc-ro.br Teora da Probabldade Modelo ateátco que perte estudar, de fora abstrata,
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
Centro de massa Dinâmica do corpo rígido
 Cetro de assa Dâca do corpo rígdo Nota: As fotografas assaladas co () fora retradas do lvro () A. Bello, C. Portela e H. Caldera Rtos e Mudaça, Porto edtora. As restates são retradas de Sears e Zeasky
Cetro de assa Dâca do corpo rígdo Nota: As fotografas assaladas co () fora retradas do lvro () A. Bello, C. Portela e H. Caldera Rtos e Mudaça, Porto edtora. As restates são retradas de Sears e Zeasky
Síntese de Transformadores de Quarto de Onda
 . Sítese de rasforadores de Quarto de Oda. Itrodução rasforadores de guia de oda são aplaete epregados o projeto de copoetes e oda guiada e são ecotrados e praticaete todas as cadeias alietadoras de ateas
. Sítese de rasforadores de Quarto de Oda. Itrodução rasforadores de guia de oda são aplaete epregados o projeto de copoetes e oda guiada e são ecotrados e praticaete todas as cadeias alietadoras de ateas
Estatística: uma definição
 Prof. Lorí Val, Dr. val@pucrs.br http://.pucrs.br/faat/val/ Estatístca: ua defção Coleção de úeros estatístcas O úero de carros veddos auetou e 30%. o país A taa de deseprego atge, este ês, 7,%. As ações
Prof. Lorí Val, Dr. val@pucrs.br http://.pucrs.br/faat/val/ Estatístca: ua defção Coleção de úeros estatístcas O úero de carros veddos auetou e 30%. o país A taa de deseprego atge, este ês, 7,%. As ações
A ciência de coletar, organizar, apresentar, analisar e interpretar dados numéricos com o objetivo de tomar melhores decisões.
 .pucrs.br/faat/val/.at.ufrgs.br/~val/ Prof. Lorí Val, Dr. val@at.ufrgs.br val@pucrs.br Coleção de úeros estatístcas O úe ro de carros ve ddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%.
.pucrs.br/faat/val/.at.ufrgs.br/~val/ Prof. Lorí Val, Dr. val@at.ufrgs.br val@pucrs.br Coleção de úeros estatístcas O úe ro de carros ve ddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%.
Bioestatística Curso de Saúde. Linha Reta 2 Parábola ou curva do segundo grau. terceiro grau curva do quarto. grau curva de grau n Hipérbole
 Teora da Correlação: Probleas relatvos à correlação são aqueles que procura estabelecer quão be ua relação lear ou de outra espéce descreve ou eplca a relação etre duas varáves. Se todos os valores as
Teora da Correlação: Probleas relatvos à correlação são aqueles que procura estabelecer quão be ua relação lear ou de outra espéce descreve ou eplca a relação etre duas varáves. Se todos os valores as
4 REPRESENTAÇÃO E/S NO DOMÍNIO TRANSFORMADO (funções de transferência)
 4 REPRESENTAÇÃO E/S NO DOMÍNIO TRANSFORMADO (fuções de trasferêa) 4. Trasforada de Laplae É u operador lear, que opera sobre fuções de varável otíua postva, defdo por: L f(t) = f(s) = f(t) e -st dt Nota:
4 REPRESENTAÇÃO E/S NO DOMÍNIO TRANSFORMADO (fuções de trasferêa) 4. Trasforada de Laplae É u operador lear, que opera sobre fuções de varável otíua postva, defdo por: L f(t) = f(s) = f(t) e -st dt Nota:
Estatística: uma definição
 Prof. Lorí Val, Dr. val@at.ufrgs.br http://.at.ufrgs.br/~val/ Estatístca: ua defção Coleção de úeros estatístcas O úero de carros veddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%. As ações
Prof. Lorí Val, Dr. val@at.ufrgs.br http://.at.ufrgs.br/~val/ Estatístca: ua defção Coleção de úeros estatístcas O úero de carros veddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%. As ações
A ciência de coletar, organizar, apresentar, analisar e interpretar dados numéricos com o objetivo de tomar melhores decisões.
 Prof. Lorí Val, Dr. val@at.ufrgs.br http://.at.ufrgs.br/~val/ Coleção de úeros estatístcas stcas O úero de carros veddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%. As ações a da Telebrás
Prof. Lorí Val, Dr. val@at.ufrgs.br http://.at.ufrgs.br/~val/ Coleção de úeros estatístcas stcas O úero de carros veddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%. As ações a da Telebrás
SOLUÇÃO DE EQUAÇÕES DIFERENCIAIS POR DIFERENÇAS FINITAS-JM Balthazar- Maio Resolvendo um Problema de Condução de Calor
 SOLUÇÃO DE EQUAÇÕES DIFERENCIAIS POR DIFERENÇAS FINIAS-JM Balthazar- Mao 3 Resolvedo u Problea de Codução de Calor Para troduzr o étodo das dfereças ftas de ua fora prátca vaos cosderar u problea de codução
SOLUÇÃO DE EQUAÇÕES DIFERENCIAIS POR DIFERENÇAS FINIAS-JM Balthazar- Mao 3 Resolvedo u Problea de Codução de Calor Para troduzr o étodo das dfereças ftas de ua fora prátca vaos cosderar u problea de codução
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA
 INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
Departamento de Informática. Modelagem Analítica do Desempenho de Sistemas de Computação. Modelagem Analítica. P x t i x t i x t i x t i
 Departaeto de Iforátca Dscpla: do Desepeho de Ssteas de Coputação Cadeas de Marov I Processos de Marov (ou PE Marovao) Sea u processo estocástco caracterzado pela seüêca de v.a s X(t ),,,, Sea X(t ) a
Departaeto de Iforátca Dscpla: do Desepeho de Ssteas de Coputação Cadeas de Marov I Processos de Marov (ou PE Marovao) Sea u processo estocástco caracterzado pela seüêca de v.a s X(t ),,,, Sea X(t ) a
Vitamina A Vitamina B Vitamina C Alimento 1 50 30 20 Alimento 2 100 40 10 Alimento 3 40 20 30
 Motvção: O prole d det Itrodução os Sstes Leres U pesso e det ecesst dgerr drete s segutes qutddes de vts: g de vt A 6 g de vt B 4 g de vt C El deve suprr sus ecessddes prtr do cosuo de três letos dferetes
Motvção: O prole d det Itrodução os Sstes Leres U pesso e det ecesst dgerr drete s segutes qutddes de vts: g de vt A 6 g de vt B 4 g de vt C El deve suprr sus ecessddes prtr do cosuo de três letos dferetes
APLICAÇÕES DE MÉTODOS DE ENERGIA A PROBLEMAS DE INSTABILIDADE DE ESTRUTURAS
 PONTIFÍCI UNIVERSIDDE CTÓLIC DO RIO DE JNEIRO DEPRTMENTO DE ENGENHRI CIVIL PLICÇÕES DE MÉTODOS DE ENERGI PROBLEMS DE INSTBILIDDE DE ESTRUTURS Julaa Bragh Ramalho Raul Rosas e Slva lua de graduação do curso
PONTIFÍCI UNIVERSIDDE CTÓLIC DO RIO DE JNEIRO DEPRTMENTO DE ENGENHRI CIVIL PLICÇÕES DE MÉTODOS DE ENERGI PROBLEMS DE INSTBILIDDE DE ESTRUTURS Julaa Bragh Ramalho Raul Rosas e Slva lua de graduação do curso
Como primeiro exemplo de uma relação de recorrência, consideremos a seguinte situação:
 Relações de Recorrêcas - Notas de aula de CAP Prof. José Carlos Becceer. Ao 6. Ua Relação de Recorrêca ou Equação de Recorrêca defe ua fução por eo de ua epressão que clu ua ou as stâcas (eores) dela esa.
Relações de Recorrêcas - Notas de aula de CAP Prof. José Carlos Becceer. Ao 6. Ua Relação de Recorrêca ou Equação de Recorrêca defe ua fução por eo de ua epressão que clu ua ou as stâcas (eores) dela esa.
Centro de massa Dinâmica do corpo rígido
 Cetro de assa Dâca do corpo rígdo Nota: As fotografas assaladas co () fora retradas do lvro () A. Bello, C. Portela e H. Caldera Rtos e Mudaça, Porto edtora. As restates são retradas de Sears e Zeasky
Cetro de assa Dâca do corpo rígdo Nota: As fotografas assaladas co () fora retradas do lvro () A. Bello, C. Portela e H. Caldera Rtos e Mudaça, Porto edtora. As restates são retradas de Sears e Zeasky
Olá, amigos concursandos de todo o Brasil!
 Matemátca Facera ICMS-RJ/008, com gabarto cometado Prof. Wager Carvalho Olá, amgos cocursados de todo o Brasl! Veremos, hoje, a prova do ICMS-RJ/008, com o gabarto cometado. - O artgo º da Le.948 de 8
Matemátca Facera ICMS-RJ/008, com gabarto cometado Prof. Wager Carvalho Olá, amgos cocursados de todo o Brasl! Veremos, hoje, a prova do ICMS-RJ/008, com o gabarto cometado. - O artgo º da Le.948 de 8
1 SISTEMA FRANCÊS DE AMORTIZAÇÃO
 scpla de Matemátca Facera 212/1 Curso de Admstração em Gestão Públca Professora Ms. Valéra Espídola Lessa EMPRÉSTIMOS Um empréstmo ou facameto pode ser feto a curto, médo ou logo prazo. zemos que um empréstmo
scpla de Matemátca Facera 212/1 Curso de Admstração em Gestão Públca Professora Ms. Valéra Espídola Lessa EMPRÉSTIMOS Um empréstmo ou facameto pode ser feto a curto, médo ou logo prazo. zemos que um empréstmo
Algoritmos de Interseções de Curvas de Bézier com Uma Aplicação à Localização de Raízes de Equações
 Algortmos de Iterseções de Curvas de Bézer com Uma Aplcação à Localzação de Raízes de Equações Rodrgo L.R. Madurera Programa de Pós-Graduação em Iformátca, PPGI, UFRJ 21941-59, Cdade Uverstára, Ilha do
Algortmos de Iterseções de Curvas de Bézer com Uma Aplcação à Localzação de Raízes de Equações Rodrgo L.R. Madurera Programa de Pós-Graduação em Iformátca, PPGI, UFRJ 21941-59, Cdade Uverstára, Ilha do
Neste capítulo pretende-se introduzir o conceito de centróide, em especial quando aplicado para o caso de superfícies planas.
 Físca plcada à Egehara vl II aulo Medes ENTRÓIDES Neste capítulo pretede-se troduzr o coceto de cetróde, em especal quado aplcado para o caso de superfíces plaas. Este documeto, costtu apeas um strumeto
Físca plcada à Egehara vl II aulo Medes ENTRÓIDES Neste capítulo pretede-se troduzr o coceto de cetróde, em especal quado aplcado para o caso de superfíces plaas. Este documeto, costtu apeas um strumeto
SIMULAÇÃO DE SISTEMAS CAOTICOS NO MICROMEDIA FLASC
 Aas do XXXIV COBENGE. Passo Fudo: Ed. Uversdade de Passo Fudo Setebro de 006. ISBN 85-755-7- SIMULAÇÃO DE SISTEMAS CAOTICOS NO MICROMEDIA FLASC José Slvéro Edudo Gerao - slvero@ta.br ITA Isttuto Tecológco
Aas do XXXIV COBENGE. Passo Fudo: Ed. Uversdade de Passo Fudo Setebro de 006. ISBN 85-755-7- SIMULAÇÃO DE SISTEMAS CAOTICOS NO MICROMEDIA FLASC José Slvéro Edudo Gerao - slvero@ta.br ITA Isttuto Tecológco
3 Precificação de resseguro
 Precfcação de Resseguro 35 3 Precfcação de resseguro Este capítulo traz prmeramete uma oção ampla das aplcações das metodologas de precfcação de resseguro para melhor compreesão do mesmo Da seção 3 até
Precfcação de Resseguro 35 3 Precfcação de resseguro Este capítulo traz prmeramete uma oção ampla das aplcações das metodologas de precfcação de resseguro para melhor compreesão do mesmo Da seção 3 até
Os Fundamentos da Física (8 a edição)
 TEM ESPEI ENTRO DE MSS 1 Os Fudaetos da Físca (8 a edção) R MHO, N IOU E T OEDO Tea especal ENTRO DE MSS 1. etro de gradade e cetro de assa, 1. Propredade da cocetração de assas,. Propredade de setra,
TEM ESPEI ENTRO DE MSS 1 Os Fudaetos da Físca (8 a edção) R MHO, N IOU E T OEDO Tea especal ENTRO DE MSS 1. etro de gradade e cetro de assa, 1. Propredade da cocetração de assas,. Propredade de setra,
Palavras-chave: Problemas de corte e empacotamento, carregamento de contêineres com múltiplos destinos, otimização combinatória, modelagem matemática.
 1 ABORDAGENS PARA PROBEMAS DE CARREGAMENTO DE CONTÊINERES COM CONSIDERAÇÕES DE MÚTIPOS DESTINOS eoardo Juquera Realdo Morabto Dese Sato Yaashta Departaeto de Egehara de Produção Uversdade Federal de São
1 ABORDAGENS PARA PROBEMAS DE CARREGAMENTO DE CONTÊINERES COM CONSIDERAÇÕES DE MÚTIPOS DESTINOS eoardo Juquera Realdo Morabto Dese Sato Yaashta Departaeto de Egehara de Produção Uversdade Federal de São
CAPÍTULO VIII DIFERENCIAIS DE ORDEM SUPERIOR FÓRMULA DE TAYLOR E APLICAÇÕES
 CAPÍTULO VIII DIFERENCIAIS DE ORDEM SUPERIOR FÓRMULA DE TAYLOR E APLICAÇÕES. Dferecas de orde superor Tratareos apeas o caso das fuções de A R e R sedo que o caso geral das fuções de A R e R se obté a
CAPÍTULO VIII DIFERENCIAIS DE ORDEM SUPERIOR FÓRMULA DE TAYLOR E APLICAÇÕES. Dferecas de orde superor Tratareos apeas o caso das fuções de A R e R sedo que o caso geral das fuções de A R e R se obté a
SUBSTITUIÇÕES ENVOLVENDO NÚMEROS COMPLEXOS Diego Veloso Uchôa
 Nível Avaçado SUBSTITUIÇÕES ENVOLVENDO NÚMEROS COMPLEXOS Dego Veloso Uchôa É bastate útl e probleas de olpíada ode teos gualdades ou quereos ecotrar u valor de u soatóro fazeros substtuções por úeros coplexos
Nível Avaçado SUBSTITUIÇÕES ENVOLVENDO NÚMEROS COMPLEXOS Dego Veloso Uchôa É bastate útl e probleas de olpíada ode teos gualdades ou quereos ecotrar u valor de u soatóro fazeros substtuções por úeros coplexos
2 Avaliação da segurança dinâmica de sistemas de energia elétrica: Teoria
 Avalação da seguraça dâmca de sstemas de eerga elétrca: Teora. Itrodução A avalação da seguraça dâmca é realzada através de estudos de establdade trastóra. Nesses estudos, aalsa-se o comportameto dos geradores
Avalação da seguraça dâmca de sstemas de eerga elétrca: Teora. Itrodução A avalação da seguraça dâmca é realzada através de estudos de establdade trastóra. Nesses estudos, aalsa-se o comportameto dos geradores
Consideremos a fórmula que nos dá a área de um triângulo: = 2
 6. Cálculo Derecal e IR 6.. Fução Real de Varáves Reas Cosdereos a órula que os dá a área de u trâulo: b h A( b h) Coo podeos vercar a área de u trâulo depede de duas varáves: base (b) e altura (h) Podeos
6. Cálculo Derecal e IR 6.. Fução Real de Varáves Reas Cosdereos a órula que os dá a área de u trâulo: b h A( b h) Coo podeos vercar a área de u trâulo depede de duas varáves: base (b) e altura (h) Podeos
Forma padrão do modelo de Programação Linear
 POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
Capitulo 8 Resolução de Exercícios
 FORMULÁRIO Audades Peródcas, Crescetes e Postecpadas, com Termos em P. A. G 1 1 1 1 G SPAC R R s s 1 1 1 1 1 G G C R a R a 1 1 PAC Audades Gradetes Postecpadas S GP G 1 1 ; C GP G 1 1 1 Audades Gradetes
FORMULÁRIO Audades Peródcas, Crescetes e Postecpadas, com Termos em P. A. G 1 1 1 1 G SPAC R R s s 1 1 1 1 1 G G C R a R a 1 1 PAC Audades Gradetes Postecpadas S GP G 1 1 ; C GP G 1 1 1 Audades Gradetes
Programação Paralela
 rograação aralela FEU 4. Avalação de steas aralelos Defções Razão etre a velocdade de processaeto coseguda o sstea paralelo e a velocdade coseguda co u processador (pouca foração...) Efcêca Quocete do
rograação aralela FEU 4. Avalação de steas aralelos Defções Razão etre a velocdade de processaeto coseguda o sstea paralelo e a velocdade coseguda co u processador (pouca foração...) Efcêca Quocete do
6. Inferência para Duas Populações USP-ICMC-SME 2013
 6. Iferêca ara Duas Poulações UP-ICMC-ME 3 8.. Poulações deedetes co dstrbução oral Poulação Poulação,,,, ~ N, ~ N, ~ N, Obs. e a dstrbução de e/ou ão for oral, os resultados são váldos aroxadaete. Testes
6. Iferêca ara Duas Poulações UP-ICMC-ME 3 8.. Poulações deedetes co dstrbução oral Poulação Poulação,,,, ~ N, ~ N, ~ N, Obs. e a dstrbução de e/ou ão for oral, os resultados são váldos aroxadaete. Testes
MÉTODO COMPUTACIONAL AUTOMÁTICO TICO PARA PRÉ-PROCESSAMENTO PROCESSAMENTO DE IMAGENS RADIOGRÁFICAS. M. Z. Nascimento, A. F. Frère e L. A.
 MÉTODO COMPUTACIONAL AUTOMÁTICO TICO PARA PRÉ-PROCESSAMENTO PROCESSAMENTO DE IMAGENS RADIOGRÁFICAS M. Z. Nascmeto, A. F. Frère e L. A. Neves INTRODUÇÃO O cotraste as radografas vara ao logo do campo de
MÉTODO COMPUTACIONAL AUTOMÁTICO TICO PARA PRÉ-PROCESSAMENTO PROCESSAMENTO DE IMAGENS RADIOGRÁFICAS M. Z. Nascmeto, A. F. Frère e L. A. Neves INTRODUÇÃO O cotraste as radografas vara ao logo do campo de
QUESTÕES DISCURSIVAS Módulo
 QUESTÕES DISCURSIVAS Módulo 0 009 D (FUVEST-SP 008 A fgura ao lado represeta o úero + o plao coplexo, sedo a udade agára Nessas codções, a detere as partes real e agára de e b represete e a fgura a segur
QUESTÕES DISCURSIVAS Módulo 0 009 D (FUVEST-SP 008 A fgura ao lado represeta o úero + o plao coplexo, sedo a udade agára Nessas codções, a detere as partes real e agára de e b represete e a fgura a segur
Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto
 Faculdade de Ecooma, Admstração e Cotabldade de Rberão Preto Ecooma Moetára Curso de Ecooma / º. Semestre de 014 Profa. Dra. Rosel da Slva Nota de aula CAPM Itrodução Há dos modelos bastate utlzados para
Faculdade de Ecooma, Admstração e Cotabldade de Rberão Preto Ecooma Moetára Curso de Ecooma / º. Semestre de 014 Profa. Dra. Rosel da Slva Nota de aula CAPM Itrodução Há dos modelos bastate utlzados para
Econometria: 3 - Regressão Múltipla
 Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Estudo das relações entre peso e altura de estudantes de estatística através da análise de regressão simples.
 Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Estatística Notas de Aulas ESTATÍSTICA. Notas de Aulas. Professor Inácio Andruski Guimarães, DSc. Professor Inácio Andruski Guimarães, DSc.
 Estatístca Notas de Aulas ESTATÍSTICA Notas de Aulas Professor Iáco Adrus Gumarães, DSc. Professor Iáco Adrus Gumarães, DSc. Estatístca Notas de Aulas SUMÁRIO CONCEITOS BÁSICOS 5. Estatístca. Estatístca
Estatístca Notas de Aulas ESTATÍSTICA Notas de Aulas Professor Iáco Adrus Gumarães, DSc. Professor Iáco Adrus Gumarães, DSc. Estatístca Notas de Aulas SUMÁRIO CONCEITOS BÁSICOS 5. Estatístca. Estatístca
INFERÊNCIA ESTATÍSTICA PARA DUAS POPULAÇÕES
 INFERÊNCIA ESTATÍSTICA PARA DUAS POPULAÇÕES . Populações depedetes co dstrbução oral População População,, Y,,Y ~ N, Y ~ N, Y ~ N, Obs. Se a dstrbução de e/ou Y ão for oral, os resultados são váldos aproxadaete.
INFERÊNCIA ESTATÍSTICA PARA DUAS POPULAÇÕES . Populações depedetes co dstrbução oral População População,, Y,,Y ~ N, Y ~ N, Y ~ N, Obs. Se a dstrbução de e/ou Y ão for oral, os resultados são váldos aproxadaete.
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
CAPÍTULO 2 - Estatística Descritiva
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
ANÁLISE DE ERROS. Todas as medidas das grandezas físicas deverão estar sempre acompanhadas da sua dimensão (unidades)! ERROS
 ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
16/03/2014. IV. Juros: taxa efetiva, equivalente e proporcional. IV.1 Taxa efetiva. IV.2 Taxas proporcionais. Definição:
 6// IV. Juros: taxa efetva, equvalete e proporcoal Matemátca Facera Aplcada ao Mercado Facero e de Captas Professor Roaldo Távora IV. Taxa efetva Defção: É a taxa de juros em que a udade referecal de seu
6// IV. Juros: taxa efetva, equvalete e proporcoal Matemátca Facera Aplcada ao Mercado Facero e de Captas Professor Roaldo Távora IV. Taxa efetva Defção: É a taxa de juros em que a udade referecal de seu
AÇÕES E COMBINAÇÕES DAS AÇÕES
 AÇÕES E COMBINAÇÕES DAS AÇÕES 1. INTRODUÇÃO As oras brasileiras para projetos de estruturas especifica que u projeto é coposto por eorial justificativo, desehos e, tabé por plao de execução quado há particularidades
AÇÕES E COMBINAÇÕES DAS AÇÕES 1. INTRODUÇÃO As oras brasileiras para projetos de estruturas especifica que u projeto é coposto por eorial justificativo, desehos e, tabé por plao de execução quado há particularidades
CAP RATES, YIELDS E AVALIAÇÃO DE IMÓVEIS pelo método do rendimento
 CAP RATES, YIELDS E AALIAÇÃO DE IMÓEIS pelo étodo do rendento Publcado no Confdencal Iobláro, Março de 2007 AMARO NAES LAIA Drector da Pós-Graduação de Gestão e Avalação Ioblára do ISEG. Docente das caderas
CAP RATES, YIELDS E AALIAÇÃO DE IMÓEIS pelo étodo do rendento Publcado no Confdencal Iobláro, Março de 2007 AMARO NAES LAIA Drector da Pós-Graduação de Gestão e Avalação Ioblára do ISEG. Docente das caderas
CAPÍTULO III MÉTODOS DE RUNGE-KUTTA
 PMR 40 Mecâca Coputacoal CAPÍTULO III MÉTODOS DE RUNGE-KUTTA São étodos de passo sples requere apeas dervadas de prera orde e pode forecer aproxações precsas co erros de trucaeto da orde de, 3, 4, etc.
PMR 40 Mecâca Coputacoal CAPÍTULO III MÉTODOS DE RUNGE-KUTTA São étodos de passo sples requere apeas dervadas de prera orde e pode forecer aproxações precsas co erros de trucaeto da orde de, 3, 4, etc.
MAE116 Noções de Estatística
 Grupo C - º semestre de 004 Exercíco 0 (3,5 potos) Uma pesqusa com usuáros de trasporte coletvo a cdade de São Paulo dagou sobre os dferetes tpos usados as suas locomoções dáras. Detre ôbus, metrô e trem,
Grupo C - º semestre de 004 Exercíco 0 (3,5 potos) Uma pesqusa com usuáros de trasporte coletvo a cdade de São Paulo dagou sobre os dferetes tpos usados as suas locomoções dáras. Detre ôbus, metrô e trem,
Projeto de rede na cadeia de suprimentos
 Projeto de rede a cadea de suprmetos Prof. Ph.D. Cláudo F. Rosso Egehara Logístca II Esboço O papel do projeto de rede a cadea de suprmetos Fatores que fluecam decsões de projeto de rede Modelo para decsões
Projeto de rede a cadea de suprmetos Prof. Ph.D. Cláudo F. Rosso Egehara Logístca II Esboço O papel do projeto de rede a cadea de suprmetos Fatores que fluecam decsões de projeto de rede Modelo para decsões
Relatório 2ª Atividade Formativa UC ECS
 Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
(1) no domínio : 0 x < 1, : constante não negativa. Sujeita às condições de contorno: (2-a) (2-b) CC2: 0
 EXEMPLO MOTIVADO II EXEMPLO MOTIVADO II Método da Apromação Polomal Aplcado a Problemas Udrecoas sem Smetra. Equações Dferecas Ordáras Problemas de Valores o otoro Estrutura Geral do Problema: dy() d y()
EXEMPLO MOTIVADO II EXEMPLO MOTIVADO II Método da Apromação Polomal Aplcado a Problemas Udrecoas sem Smetra. Equações Dferecas Ordáras Problemas de Valores o otoro Estrutura Geral do Problema: dy() d y()
Capítulo 1 PORCENTAGEM
 Professor Joselas Satos da Slva Matemátca Facera Capítulo PORCETAGEM. PORCETAGEM A porcetagem ada mas é do que uma otação ( % ) usada para represetar uma parte de cem partes. Isto é, 20% lê-se 20 por ceto,
Professor Joselas Satos da Slva Matemátca Facera Capítulo PORCETAGEM. PORCETAGEM A porcetagem ada mas é do que uma otação ( % ) usada para represetar uma parte de cem partes. Isto é, 20% lê-se 20 por ceto,
E-mails: damasceno1204@yahoo.com.br damasceno@interjato.com.br damasceno12@hotmail.com http://www. damasceno.info www. damasceno.info damasceno.
 Matemátca Facera 2007.1 Prof.: Luz Gozaga Damasceo 1 E-mals: damasceo1204@yahoo.com.br damasceo@terjato.com.br damasceo12@hotmal.com http://www. damasceo.fo www. damasceo.fo damasceo.fo Obs.: (1 Quado
Matemátca Facera 2007.1 Prof.: Luz Gozaga Damasceo 1 E-mals: damasceo1204@yahoo.com.br damasceo@terjato.com.br damasceo12@hotmal.com http://www. damasceo.fo www. damasceo.fo damasceo.fo Obs.: (1 Quado
Professor Mauricio Lutz REGRESSÃO LINEAR SIMPLES. Vamos, então, calcular os valores dos parâmetros a e b com a ajuda das formulas: ö ; ø.
 Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
MODELO DE ISING BIDIMENSIONAL SEGUNDO A TÉCNICA DE MATRIZ DE TRANSFERÊNCIA
 UIVERSIDADE ESTADUAL DO CEARÁ RAFAEL DE LIMA BARBOSA MODELO DE ISIG BIDIMESIOAL SEGUDO A TÉCICA DE MATRIZ DE TRASFERÊCIA FORTALEZA CEARÁ 4 RAFAEL DE LIMA BARBOSA MODELO DE ISIG BIDIMESIOAL SEGUDO A TÉCICA
UIVERSIDADE ESTADUAL DO CEARÁ RAFAEL DE LIMA BARBOSA MODELO DE ISIG BIDIMESIOAL SEGUDO A TÉCICA DE MATRIZ DE TRASFERÊCIA FORTALEZA CEARÁ 4 RAFAEL DE LIMA BARBOSA MODELO DE ISIG BIDIMESIOAL SEGUDO A TÉCICA
8. INFERÊNCIA PARA DUAS POPULAÇÕES
 8 INFERÊNCIA PARA UA POPULAÇÕE 8 Populações depedetes co dstrbução oral População População, L, Y, L,Y ~ N, σ Y ~ N, σ σ σ Y ~ N, Obs e a dstrbução de e/ou Y ão for oral, os resultados são váldos aproxadaete
8 INFERÊNCIA PARA UA POPULAÇÕE 8 Populações depedetes co dstrbução oral População População, L, Y, L,Y ~ N, σ Y ~ N, σ σ σ Y ~ N, Obs e a dstrbução de e/ou Y ão for oral, os resultados são váldos aproxadaete
AN EVALUATION OF THE EFFICIENCY OF THE BRAZILIAN MUNICIPALITIES IN THE PROVISION OF PUBLIC SERVICES USING DATA ENVELOPMENT ANALYSIS.
 AN EVALUATION OF THE EFFICIENCY OF THE BRAZILIAN MUNICIPALITIES IN THE PROVISION OF PUBLIC SERVICES USING DATA ENVELOPMENT ANALYSIS. Rogéro Bouer Brazla Isttute for Appled Ecooc Research Catholc Uverst
AN EVALUATION OF THE EFFICIENCY OF THE BRAZILIAN MUNICIPALITIES IN THE PROVISION OF PUBLIC SERVICES USING DATA ENVELOPMENT ANALYSIS. Rogéro Bouer Brazla Isttute for Appled Ecooc Research Catholc Uverst
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística
 Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
2. MODELO DETALHADO: Relações de Recorrência. Exemplo: Algoritmo Recursivo para Cálculo do Fatorial Substituição Repetida
 . MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
. MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
A Medição e o Erro de Medição
 A Medção e o Erro de Medção Sumáro 1.1 Itrodução 1.2 Defções 1.3 Caracterzação da qualdade de medção 1.4 O erro da medção 1.4.1 Os erros aleatóros 1.4.2 Os erros sstemátcos 1.5 O verdadero valor, o erro
A Medção e o Erro de Medção Sumáro 1.1 Itrodução 1.2 Defções 1.3 Caracterzação da qualdade de medção 1.4 O erro da medção 1.4.1 Os erros aleatóros 1.4.2 Os erros sstemátcos 1.5 O verdadero valor, o erro
Métodos iterativos. Capítulo O Método de Jacobi
 Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
MEDIDAS DE DISPERSÃO:
 MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
Momento Linear duma partícula
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Mometo lear de uma partícula e de um sstema de partículas. - Le fudametal da dâmca para um sstema de partículas. - Impulso
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Mometo lear de uma partícula e de um sstema de partículas. - Le fudametal da dâmca para um sstema de partículas. - Impulso
PROCEDIMENTOS DE CÁLCULO DE INCERTEZA DE MEDIÇÃO EM MEDIÇÕES DIRETAS E INDIRETAS
 PROCEDIMENTOS DE CÁLCULO DE INCERTEZA DE MEDIÇÃO EM MEDIÇÕES DIRETAS E INDIRETAS Prof José Leoardo Noroha M Eg Departameto de Egehara de Prodção Escola Federal de Egehara de Itabá EFEI RESUMO: Neste trabalho
PROCEDIMENTOS DE CÁLCULO DE INCERTEZA DE MEDIÇÃO EM MEDIÇÕES DIRETAS E INDIRETAS Prof José Leoardo Noroha M Eg Departameto de Egehara de Prodção Escola Federal de Egehara de Itabá EFEI RESUMO: Neste trabalho
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
AULA Produto interno em espaços vectoriais reais ou complexos Produto Interno. Norma. Distância.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Capítulo 5 EQUAÇÕES DE CONSERVAÇÃO DA MASSA
 Capítulo 5 EQUAÇÕES DE CONSERVAÇÃO DA MASSA O objetvo deste capítulo é apresetar formas da equação da coservação da massa em fução de propredades tesvas faclmete mesuráves, como a temperatura, a pressão,
Capítulo 5 EQUAÇÕES DE CONSERVAÇÃO DA MASSA O objetvo deste capítulo é apresetar formas da equação da coservação da massa em fução de propredades tesvas faclmete mesuráves, como a temperatura, a pressão,
Cálculo Numérico Interpolação Polinomial Ajuste de Curvas (Parte II)
 Cálulo Nuéro Iterpolação Poloal Ajuste de Curvas (Parte II) Pro Jore Cavalat joreavalat@uvasedubr MATERIAL ADAPTADO DOS SLIDES DA DISCIPLINA CÁLCULO NUMÉRICO DA UFCG - wwwdsuedubr/~u/ Ajuste de Curvas
Cálulo Nuéro Iterpolação Poloal Ajuste de Curvas (Parte II) Pro Jore Cavalat joreavalat@uvasedubr MATERIAL ADAPTADO DOS SLIDES DA DISCIPLINA CÁLCULO NUMÉRICO DA UFCG - wwwdsuedubr/~u/ Ajuste de Curvas
Nas Instituições de Ensino Superior(IES), há uma relação direta entre a qualidade do ensino e a taxa de inadimplência. A taxa de inadimplência das
 CORRELAÇÃO Nas Isttuções de Eso Superor(IES), há uma relação dreta etre a qualdade do eso e a taxa de admplêca. A taxa de admplêca das IES que obtveram cocetos A e B o Provão é,%, as que obtveram C é 6%
CORRELAÇÃO Nas Isttuções de Eso Superor(IES), há uma relação dreta etre a qualdade do eso e a taxa de admplêca. A taxa de admplêca das IES que obtveram cocetos A e B o Provão é,%, as que obtveram C é 6%
RACIOCÍNIO LÓGICO / ESTATÍSTICA LISTA 2 RESUMO TEÓRICO
 RACIOCÍIO LÓGICO - Zé Carlos RACIOCÍIO LÓGICO / ESTATÍSTICA LISTA RESUMO TEÓRICO I. Cocetos Icas. O desvo médo (DM), é a méda artmétca dos desvos de cada dado da amostra em toro do valor médo, sto é x
RACIOCÍIO LÓGICO - Zé Carlos RACIOCÍIO LÓGICO / ESTATÍSTICA LISTA RESUMO TEÓRICO I. Cocetos Icas. O desvo médo (DM), é a méda artmétca dos desvos de cada dado da amostra em toro do valor médo, sto é x
Prof. Alvaro Vannucci
 Pro. Alvaro Vaucc Lebreos o roblea dos sucessvos deslocaetos aleatóros rado - DRUNK - walk Cosderaos cada deslocaeto asso dado ela essoa coo tedo sere o eso coreto L. Chaaos de a robabldade de asso ara
Pro. Alvaro Vaucc Lebreos o roblea dos sucessvos deslocaetos aleatóros rado - DRUNK - walk Cosderaos cada deslocaeto asso dado ela essoa coo tedo sere o eso coreto L. Chaaos de a robabldade de asso ara
Matemática Financeira
 Cocetos Báscos de Matemátca Facera Uversdade do Porto Faculdade de Egehara Mestrado Itegrado em Egehara Electrotécca e de Computadores Ecooma e Gestão Na prátca As decsões faceras evolvem frequetemete
Cocetos Báscos de Matemátca Facera Uversdade do Porto Faculdade de Egehara Mestrado Itegrado em Egehara Electrotécca e de Computadores Ecooma e Gestão Na prátca As decsões faceras evolvem frequetemete
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
CAPÍTULO 3 MEDIDAS DE TENDÊNCIA CENTRAL E VARIABILIDADE PPGEP Medidas de Tendência Central Média Aritmética para Dados Agrupados
 3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
